关于自对偶平图的平衡划分的一个结论

沈云星

（福建农林大学 金山学院，福建 福州 350002）

1 引言

图的顶点划分问题是图论研究中的一个重要问题.它在超大规模集成电路设计中有着重要的作用.最大割问题是一个著名的问题，就是寻找图的一个顶点划分V(G)=V1⋃V2使得 e (V1, V2)最大，其中e(V1, V2)表示满足两个端点分别在不同子集V1和V2的边的数目.一个图G的划分V(G)=V1⋃V2称为G的平衡二部划分如果满足-1≤ |V1|- | V2|≤1.用(V1, V2)表示二部划分V(G)=V1⋃V2.图的最小平衡二部划分问题，就是寻求顶点集的一个平衡二部划分(V1,V2)使得e(V1,V2)最小.这是一个NP-难的问题，对于平图，关于这个问题的复杂性[1]至今还是未知的.很多学者致力于一些特殊图类或具有限制条件的平图[2]的研究.

设V(G),E(G)分别表示图G的顶点集合、边集合.设 Φ≠S⊆V(G)，用Ns(u)表示u∈V(G)的邻点在S中的这些点构成的集合.G[S]表示以S为顶点集，以两端点均在S中的边的全体为边集所组成的子图.用[u , v ]表示图G的一个圈C上按顺时针方向从u到v的所有顶点（包含u，v）.用K2+e表示K2加上一条边得到的图.

猜想[2]提出：一个阶为n的平图存在平衡二部划分(V1, V2)满足e(V1, V2)≤n.

本文证明了具有n个顶点的自对偶平图存在平衡二部划分(V1, V2)使得e(V1, V2)≤n，并且还给出了它的一类极图，只有K4和K2+e.

在第二部分中，先给出关于自对偶平图的定义、性质和几个有用的引理，主要结论和证明过程在第三部分完成.

2 相关的定义、性质及引理

定义2.1[3]如果一个图能画在平面上使得它的边仅在端点相交，则称这个图为可嵌入平面的或平面图，将平面图的平面嵌入称为平图.

定义2.2[3]给出平图G，定义另一个图G*如下：对于G的每个面 f，都有G*的顶点 f*与之对应；对于G的每一条边e，都有G*的边e*与之对应；G*中顶点 f*与g*由e*连接，当且仅当G中与顶点 f*和 g*对应的面 f和g被边e分隔.图G*称为G的对偶图.

定义2.3[3]若一个平图G与它的对偶图G*同构，则称G为自对偶平图.

性质2.1 设G是自对偶平图，则G是连通的.

证明设 G*是G的对偶图，由对偶图的性质可知：G*连通，且由于G是自对偶的，所以G也连通.

性质2.2 一个具有n个顶点，m条边，r个面的自对偶平图G满足m=2n-2.

证明由于G是自对偶的，从而 n=r.由性质2.1，G满足欧拉公式，即 n -m+r=2，从而得到m=2n-2.

引理2.1[2]设(V1, V2)是G中使得e(V1, V2)为最小的平衡二部划分，则对于任意的一对顶点ui∈V1和vj∈ V2，有：|NV1(ui) |+ | NV2(vj)|≥ |NV2(ui)|+ | NV1(vj) |，uivj∉ E (G ) 和 | NV1(ui)|+ | NV2(vj)|≥ |NV2(ui)|+ | NV1(vj)|-2 ，uivj∈E(G ) .

引理2.2（Kuratowski定理[3]） 一个图是平面图当且仅当它不含有K5或K3,3的剖分图.

引理2.3[3]设G连通且S是V(G ) 的非空真子集，Sˉ=V(G)S，则边割[S , S ˉ]是G的键当且仅当G[S]和G[Sˉ] 都连通.

引理2.4[3]设G=(V , E,F ) 是连通的平图，G*是G的对偶图，则有：

（1）如果B是G的键，则 B*是G*的圈；

（2）如果C是G的圈，则C*是G*的键.

3 主要结论

定理3.1设G是具有 ||V(G)=n，||E(G)=m的自对偶平图，则G存在平衡二部划分(V1, V2)使得e(V1, V2)≤n.且min{e ( V1, V2):(V1, V2)是G的平衡二部划分 }=n且G[V1]，G[V2]都连通，当且仅当G是 K4或K2+e.

证明先 证明第一部分

由于G是自对偶的，从而由性质2.2，得到m=2n-2.注意到G必定存在一个度为3或度为2的顶点，将其记为x，否则有4n-4≥4n，矛盾.

若n=2k+1，则令G'=G-x；若n=2k，则令G'=G，此时得到的G'也是平图.

设(V1, V2)是G'中使得eG'(V1, V2)最小的平衡二部划分，进一步假设V1={u1, u2,…,uk} ，V2={v1, v2,…,vk}.由引理2.2知，存在k-2个顶点对{ui, vj}满足ui∈V1，vj∈V2，uivj∉E(G').通过改变它们的顺序，不失一般性，假设k-2个顶点对为{ui, vi}，i≤k-2.由引理2.1知

|NV1(ui) |+ | NV2(vi)|≥ |NV2(ui)|+ | NV1(vi) |，i≤k-2和 | NV1(ui)|+ | NV2(vi)|≥ |NV2(ui)|+ | NV1(vi)|-2，i≥k-1.

将上面所有的不等式加起来，得到：

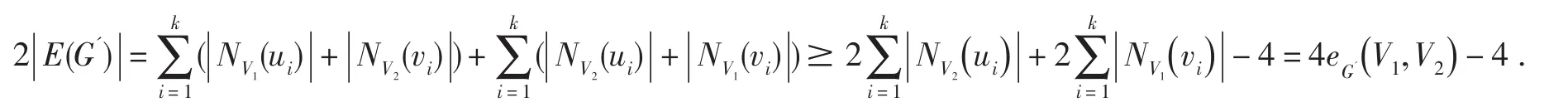
从而得到eG'(V1, V2)≤2+(| E ( G')|-2).

若 n =2k，则 | E (G')|= | E (G ) | =2n-2.此时eG(V1, V2)=eG'(V1, V2)≤2+n-2=n.

若 n =2k+1，则 | E (G')|≤ |E ( G ) | -2=2n-4.此时eG'(V1, V2)≤2+n-3=n-1.注意到dG(x)=3或dG(x)=2，现将 x 加入V1或V2，则有，其中 V1'=V1⋃{x}，或=V2⋃{x}.

综上所述，证明了G存在平衡二部划分(V1, V2)使得e(V1, V2)≤n.

下面证明第二部分.

不妨假设(V1, V2)是G中使得e(V1, V2)=n为最小的平衡二部划分且G[V1]、G[V2]是连通的.由性质2.1和引理2.3、2.4可知，图G存在一个长度为n的圈C，即是G的一个哈密顿圈.设V(C)={v1, v2,…,vn} ，分别将C的内部和外部记为Cin，Cout.下面考虑所有可能的顶点集V(G)的平衡二部划分(Vi,1,Vi,2)，形如：

（说明：当i+1,…,i+[n-12] >n时，取 i +1=(i + 1) mod n，…，i+[n-12] =(i + [n-12] )mod n.后面遇到类似情形，如此说明）

下面证明e(Vi,1,Vi,2)=n，i∈{1 , 2,…,n}.

由m=2n-2，| E ( C ) | =n可得：G中剩下n-2条边，则有

又由于此时G的最小平衡割的大小为n，所以

由（1）、（2）可知

下面根据n为偶数和奇数分两种情况进行讨论.

情形1 n=2k.

由(∗)式可知，e(Vi,1,Vi,2)=2k且e(Vi+k+1,1,Vi+k+1,2)=2k，i∈{1 , 2,…,k-1} ，所以在 Cin中，[vi, vi+k-1]和[vi+k+1,vi]没有边存在.根据 | V (C ) | =2k易知，在Cin中，vi可能的邻点只能是vi+k，i∈{1 , 2,…,k-1}.又由(∗)式可知e(Vi,1,Vi,2)=2k且e(Vi-k+1,1,Vi-k+1,2)=2k，i∈{k , k+1,…,2k} ，所以在Cin中，[vi, vi+k-1]和[vi-k+1,vi]没有边存在.根据 |V ( C ) | =2k，易知，在Cin中，vi可能的邻点只能是 vi+k，i∈{k , k+1,…,2k}.

综上可得，在Cin中，vi可能的邻点只能是vi+k，i∈{1 , 2,…,2k}.

同理可得，在Cout中，vi可能的邻点只能是vi+k，i∈{1 , 2,…,2k}.

由G的平面性和自对偶性可知，Cin和Cout中最多各含有一条边.也就是2k-2≤2⇒k≤2.由k的整数性质易知，k=1或k=2.

当k=1时，即n=2，可得G是一个长度为2的圈，记为G=K2+e.

当k=2时，即n=4，可得G是一个具有4个顶点的完全图，即G=K4.

易知：这两个图都是自对偶平图，且它们的最小平衡割的大小都为n.

情形2 n=2k+1.

由(∗)式可知，e(Vi,1,Vi,2)=2k+1且e(Vi+k+1,1,Vi+k+1,2)=2k+1，i∈{1 , 2,…,k} ，所以在 Cin中，[vi, vi+k]和[vi+k+1,vi]没有边存在.根据 | V (C ) | =2k+1易知，在 Cin中，vi没有邻点，i∈{1 , 2,…,k}.又由(∗)式可知e(Vi,1,Vi,2)=2k+1且e(Vi-k,1,Vi-k,2)=2k+1，i∈{k + 1,k+2,…,2k+1} ，所以在 Cin中，[vi, vi+k]和[vi-k,vi]没有边存在.根据 |V ( C ) | =2k+1易知，在Cin中，vi没有邻点，i∈{k + 1,k+2,…,2k+1}.

综上可得，在Cin中，vi没有邻点，i∈{1 , 2,…,2k+1}.

同理可得，在Cout中，vi没有邻点，i∈{1 , 2,…,2k+1}.

即2k-1=0⇒k=12，矛盾.

综上所述，找到了自对偶平图的一类极图，只有K4和K2+e.即定理第二部分得证.

[1]Karpinski M.On approximability of minimum bisection problem[R].Trier:Electronic Colloquium on Computational Complexity,2002.

[2]Fan G,Xu B,Yu X,et al.Upper bounds on minimum balanced bipartitions[J].Discrete Math,2012,312:1077-1083.

[3]邦迪J A，默蒂U S R.图论及其应用[M].北京：科学出版社，1984：145-161.