抽褶造型与面料性能的关系及评价模型建立

王停停，陈敏之，江 爽

(浙江理工大学服装学院，杭州 310018)

抽褶造型与面料性能的关系及评价模型建立

王停停，陈敏之，江 爽

(浙江理工大学服装学院，杭州 310018)

采用14种面料为试验面料，测试了面料主要物理性能，对不同性能的面料抽褶设计，再利用主客观评价量化服装抽褶造型，定性分析面料性能对抽褶造型的影响，并得出抽褶造型评价模型。试验结果表明：织物的面密度、经纬密度、厚度和剪切性能对抽褶波峰数、平均波深、波间距具有负影响；悬垂性能对抽褶造型下摆的宽窄和抽褶后侧面形成的造型弧度大小具有负影响；面料抽褶造型等级与抽褶波峰数和波弧角度正相关。

抽褶；面料性能；主观评价；回归分析

在服装设计中，材料对于服装风格和造型的影响表现得越来越突出，甚至成为决定设计成败的关键因素之一[1]。抽褶是以点或线为单位起褶，是面料集聚收缩或抽紧所形成的自然、丰富、无规律的纹理状态[2]。抽褶造型是服装常用装饰造型之一，造型优雅，具有强烈的立体感与流体感[3]。

在20世纪80年代国内外学者就开始研究服装的面料性能对款式造型的影响[4-7]，因此，将分析面料性能对服装抽褶造型效果的影响，由于抽褶造型变化多样，需要依据其造型特征进行划分，有利于对抽褶造型等级判别，因此，本文建立了抽褶效果造型评价模型。

1 实验

1.1 实验材料

选取了不同原料、厚度、组织结构的14种面料，其基本规格见表1。参考文献[8-10]的结果，主要研究织物的面密度、经纬密度、厚度、剪切性能、弯曲性能和悬垂性对服装抽褶造型效果的影响。

表1 面料基本规格

1.2 抽褶样板的设计

通常面料抽缩前长度为抽缩后长度的1.5倍,抽缩量也可以为2～3倍，丝绸面料抽缩量可大些[11]。本文共设计了4种抽褶量，分别是1∶1.25、1∶1.5、1∶1.75、1∶2。0号对照面料，再添加1∶1和1∶2.25两种抽褶比例，用于主观评价时的标准对照样卡。

1.3 抽褶造型效果客观测试

抽褶造型的分析重点是材料的质地与褶纹疏密效果的关系[12]，因此本文抽褶造型的客观测量分为正面数据测量、侧面数据测量，共12个测量指标。正面数据分别为缝合线以下5cm段、15cm段和底摆的波峰个数M1、平均波深M2、波峰间距M3;侧面数据为5cm段、15cm段和底摆的侧面波弧正切角tanα、tanβ和tanγ。在图1中，A点位置记为(X1,Y1),B点位置记为(X2,Y2)，C点位置记为(X3,Y3)。则5cm段、15cm段和底摆的侧面波弧正切角计算公式如下：

tanα=Y1/X1

(1)

tanβ=Y2/X2

(2)

tanγ=Y3/X3

(3)

图1 抽褶效果客观指标测量方法

1.4 抽褶造型的主观评价

抽褶效果评价方法除客观测试外有主观评价法[13]，这种评价快速、直接、高效,符合评价者的生理和心理感受,也非常接近服装消费的行为特征[14]。本实验对以0号对照面料的6种比例抽褶后的效果由弱到强设定为6个标准样，对应的等级分值分别为1、2、3、4、5、6分(表2)。

表2 面料抽褶效果主观评价标准对照样卡

2 实验结果与分析

2.1 面料抽褶造型的主观评价结果

评价人员评价抽褶造型时，选择与标准对照卡最接近的抽褶造型，并给与其对应的分值。每一块抽褶面料得到的评分取其平均值，为该抽褶面料造型的最终主观评价得分(表3)。

表3 面料抽褶效果主观评价得分值

2.2 面料性能对抽褶客观造型的影响

不同的面料可能会因为某些相似的性能而有着千丝万缕的联系，用这些性能上相似的面料制作的服装，造型上也很相似。因此，将面料按照其性能进行聚类，聚类得出三类面料：第一类面料：如1#、2#、7#、8#、12#、13#，其特点是面密度、厚度、剪切性和弯曲性都比较小；第二类面料：如3#、5#、6#、9#、11#，其特点是经纬密度小，悬垂系数大；第三类面料：如4#、10#，其特点是面密度、经纬密度、剪切性和弯曲性比较大。在对面料进行合理的聚类后，分别计算出3类面料在不同抽褶比例下的各个造型数据的平均值，见表4。

表4 聚类后面料造型数据

根据所得到三类面料的客观造型数据，得到以下结论：

a) 在相同抽褶比例下，第一类面料波峰数、平均波深、波间距较大；第三类面料波峰数、平均波深、波间距较小。这说明面料面密度、经纬密度、厚度和剪切性能对抽褶波型疏密程度和波间距具有负影响。

b) 在相同抽褶比例下，第一类面料形成的抽褶造型下摆较宽；第二类面料由于其相对悬垂系数大，形成的抽褶造型下摆较窄。这说明面料的悬垂性能对抽褶造型下摆的宽窄具有负影响。

c) 在相同抽褶比例下，第一类面料抽褶后侧面波弧正切角较大，侧面形成的造型弧度较大；第二类面料抽褶后侧面波弧正切角较小，侧面形成的造型弧度较小。这说明面料的悬垂性能对抽褶后侧面形成的造型弧度大小具有负影响。

2.3 抽褶客观造型数据与主观评价得分的相关性

由于多个客观数据指标存在一定的联系，因此需要对客观造型数据进行降维，进行因子分析。将12个客观造型指标按其数据的特征降维成2个客观造型因子，记为X1，X2。

在各个位置处的波峰个数在公因子X1上均有较高的载荷，因此称X1为波峰个数因子，侧面和底摆波弧角度在公因子X2有较高的载荷，因此称X2为波弧角度因子。降维后的二个客观造型数据因子与主观评价得分进行相关分析，从表5中可以看出，主观评价得分与客观造型因子X1和X2正相关。

表5 抽褶造型主观评价得分与客观造型数据相关系数

注:**表示在0.01水平(双侧)显著相关

建立主观评价得分与客观造型因子的回归模型，得到的模型调整R2是0.907，说明回归的拟合度很高，P值表示的是回归系数的优化程度，此值越接近0，说明回归拟合度越好，表6中每个主成分因子对应的P值都小于0.05，因此可以得到面料抽褶造型效果的评价模型：

Y=3.373+1.158X1+0.393X2

(4)

其中：Y为抽褶造型效果等级，X1为波峰个数因子，X2为波弧角度因子。

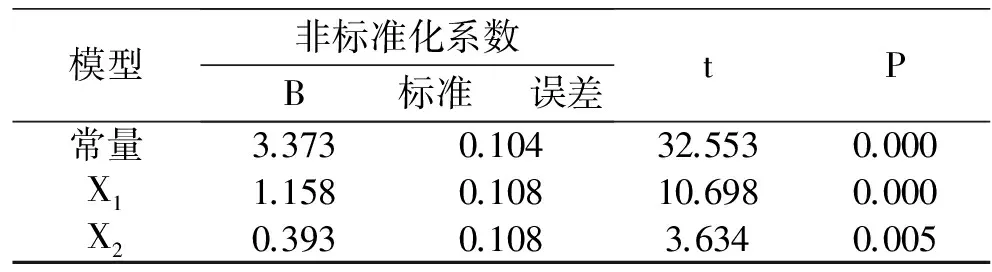
表6 抽褶造型主观评价得分与客观造型数据回归系数

3 结 论

a) 通过定性分析面料性能与抽褶造型效果之间的关系，得到织物的面密度、经纬密度、厚度和剪切性能对抽褶波峰数、平均波深、波间距具有负影响；悬垂性能对抽褶造型下摆的宽窄和抽褶后侧面形成的造型弧度大小具有负影响。对于服装企业和面料生产企业，预测面料的抽褶效果，和已知预期得到面料抽褶效果所需要开发的面料应具备的性能提供了依据。

b) 基于因子分析，抽褶客观造型特征提取为波峰个数因子和波弧角度因子。建立了抽褶造型等级与造型特征的线性回归模型，可以通过该回归模型预测和评价某抽褶造型等级。

[1] 李艳梅,张悦婷.面料性能对服装褶裥造型影响的研究[J].丝绸,2007(4):35-37.

[2] 魏 静,徐时程.服装褶纹的变化与应用[J].宁波服装职业技术学院学报,2002,12(2):11-14.

[3] 张文斌,庹 武,庄 辉.基于立体构成技术的抽褶造型与织物的相关性研[J].东华大学学报:自然科学版,2006,32(3):70-73.

[4] Roshan S. Importance of mechanical and physical properties of fabrics in the clothing manufacturing process[J].International Journal of Clothing Science and Techology,1995,7(23):35-42

[5] Ayada M, Miki M, Niwa M. Discriminating the silhouette of ladies’ garments based on fabric mechanical properties[J].International Journal of Clothing Sciences and Techhology,1991,3(3):18-27.

[6] Kawabata S, Niwa M. Objective evaluation of the quality of ladies’ garments[J]. International Journal of Clothing Science and Technology,1992,4(5):34-44.

[7] 周爱英,张明杰,张怀珠.真丝织物力学性能与服装外观造型之间的关系[J].中国纺织大学学报,1999,25(1):100-107.

[8] Thouraya H, Adel G, Faten F. A principal component analysis method for predicting the correlation between some fabric parameters and the drape[J]. Textile Research Journal,2014,14(1):22-27.

[9] Jeong Y J, Phillips D G. A study of fabric drape behaviour with image analysis part II: the effects of fahric structure and mechanical properties on fabric drape[J].Journal of the Textile Institute,1998,89(1):70-78.

[10] Ajit K P, Ameersing L, Asimananda K. Prediction of drape profile of cotton woven fabrics using artificial neural network and multiple regression method[J].Textile Research Journal,2014,81(6):560-565.

[11] 邹 平.褶饰在丝绸裙装结构设计中的应用[J].四川丝绸,2006(4):46-48.

[12] 胡 毅.礼服褶饰造型及构成技术[J].成都纺织高等专科学校学报,2005,22(1):77-81.

[13] Reham S,Tom C,Vien C,et al.Fabric and garment drape measurement[J].Journal of Fiber Bioengineering and Informatics,2013,6(1):1-22.

[14] 唐 虹,张渭源.基于面料性能的半紧身裙造型特征及预测模型[J].纺织学报,2008,29(6):88-91.

(责任编辑：许惠儿)

Relationship between Pleating Effect and Fabric Performance and Establishment of the Evaluation Model

WANGTingting,CHENMinzhi,JIANGShuang

(School of Fashion Design and Engineering, Zhejiang Sci-Tech University, Hangzhou 310018, China)

This paper uses fourteen kinds of fabric as test samples and tests the main physical properties of fabrics, using the fabrics with different performance to make pleats, analyzing qualitatively the fabric performance influence on pleating effect then obtaining evaluation model. The experimental result shows the fabric weight, density, thickness and shear performance have negative impact on the wave number , the average depth of wave and the distance; drape performance have negative impact on hem width of pleat and radian size of the side of pleat ; fabric pleating effect is associated with wave crest and wave radian size positively.

pleating; fabric performance; subjective evaluation; regression analysis

2014-12-14

王停停(1991-)，女，河南开封人，硕士研究生，研究方向为服装技术与理论。

陈敏之，E-mail：cmz_m@163.com

TS941.2

A

1009-265X(2015)04-0043-04