证明不等式的“减项”策略

陕西省武功县教育局教研室 李 歆 (邮编：712200)

证明不等式的“减项”策略

陕西省武功县教育局教研室 李 歆 (邮编：712200)

在初等数学符号里, “+”与“-”既是两个简单的运算符号,又是两个重要的性质符号,它们互相对立,又互相转化,成为表现数学思维最基本的语言形式.在数学解题中,变“+”为“-”,或者变“-”为“+”,常常可以实现思维方向的大转移.本文介绍的“-项”策略，就是在不等式的分式项(将分子看成1)前面通过添加一个“-”号后，对其分母使用均值不等式而不改变不等号方向的一种证明方法，这种方法不仅入手快,目标明,而且规律性强,操作简便,可以引发我们对这类不等式的进一步思考与研究.下面举例说明.

例1 (2003年北京市高一数学竞赛题)设a、b、c为正实数,求证:

①

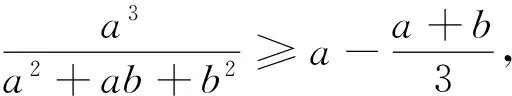
以上三式相加,得

评注 对①式稍作变化,则可以证明本题的两个类似题:

类似1 设a、b、c为正实数,求证:

类似2 设a、b、c为正实数,求证:

由42=(a+c+b+d)2≥4(a+c)(b+d)=4(ab+bc+cd)，得ab+bc+cd+da≤4，

例3(2010年首届陈省身杯全国高中数学奥林匹克) 设正实数a、b、c满足a3+b3+c3=3，证明:

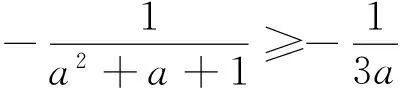
②,

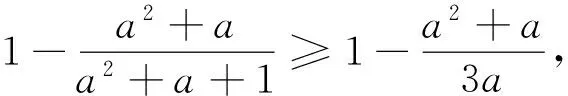
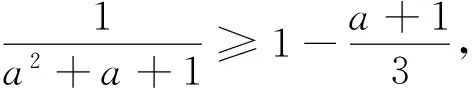
由“权方和不等式”得

即a+b+c≤3，

③

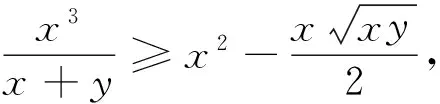
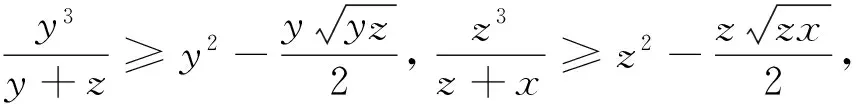
由柯西不等式,得

例5 (2011年克罗地亚数学奥林匹克)设a、b、c>0，且a+b+c=3，求证:

④

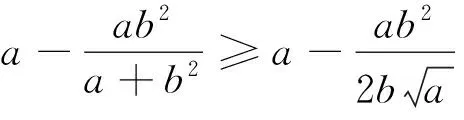
⑤

由柯西不等式,得

3(a+b+c)2=(a+b+c)(a+b+c)2

≥3(b+c+a)(ab+bc+ca)

评注 若将④式和⑤式分别变为:

则可以证明本题的一个推广:设a、b、c>0，且a+b+c=3，n∈N+，求证:

1 安振平.三十个有趣的不等式问题[J].中学数学教学参考(上旬),2011(11):58

2 徐文兵.证明不等式的搭桥术[J]. 中学数学教学参考(上旬),2012(9):58-59

2014-12-26)