一个不等式的推广与变式
2015-06-15山东省宁阳市第一中学刘才华邮编271400
中学数学教学 2015年3期
山东省宁阳市第一中学 刘才华 (邮编:271400)
一个不等式的推广与变式
山东省宁阳市第一中学 刘才华 (邮编:271400)
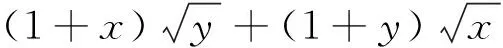
这是最近江西南昌大学附中宋庆先生提出的一个有趣的最值问题,其结果如下
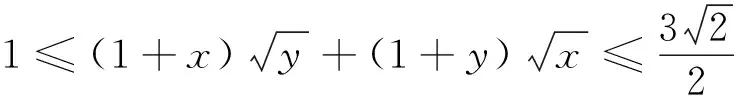
①
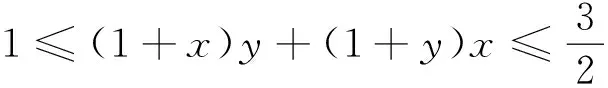
②
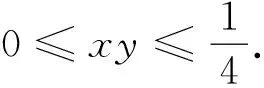
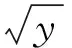
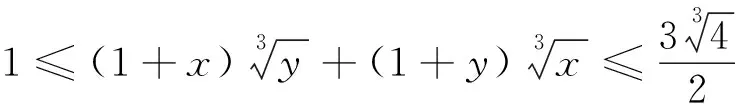
③

观察①、②、③式,并作进一步推广,得到如下
命题1 若x,y≥0,x+y=1,n≥1,n∈N,则
④
证明 由①式得
等号当且仅当x=0,y=1或x=1,y=0时成立.
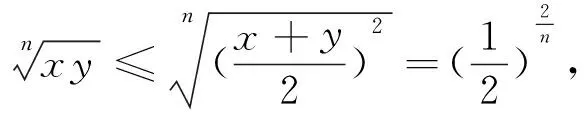
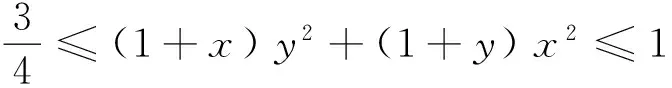
⑤
证明 由x,y≥0,x+y=1,得
由(1+x)y2+(1+y)x2=x2+y2+xy(x+y)=(x+y)2-xy=1-xy,得
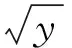
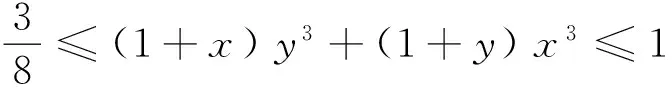
⑥

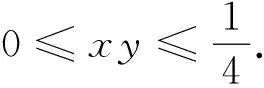
观察⑤、⑥式,并作进一步推广,得到如下

⑦
由⑤、⑥知,要证明命题2成立,只需证明n≥3,n∈N时,⑦式成立.
证明 由⑤式得(1+x)yn+(1+y)xn≤(1+x)y2+(1+y)x2≤1,等号当且仅当x=0,y=1或x=1,y=0时成立.
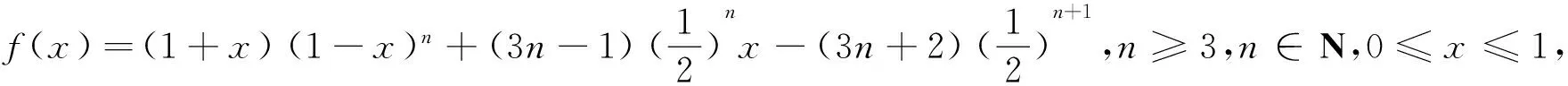

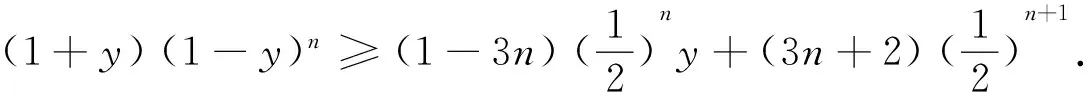
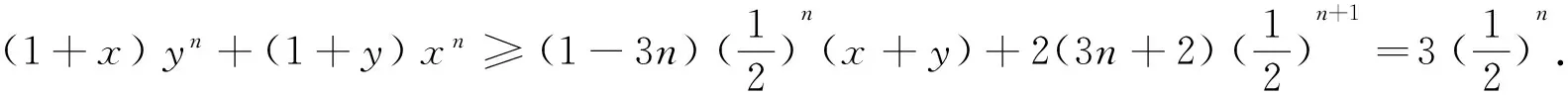
故命题2成立.
1 秦庆雄、范花妹.精彩源自深入的探索[J].数学通讯,2014(9):48-49
2015-03-26)
