基于“问题”的数学教学——从一则教学案例引发的思考

浙江省温州大学数信学院 徐彦辉 (邮编：325035)

基于“问题”的数学教学
——从一则教学案例引发的思考

浙江省温州大学数信学院 徐彦辉 (邮编：325035)

“问题”是数学的心脏,问题在数学学习和研究中有其特殊的重要性.从某种意义上来讲,数学科学的起源和发展大多是由问题引起的,数学发展的历史就是数学问题的提出和解决的历史.从问题出发,以问题带动数学学科的发展,这是数学学科发展的一条重要途径.问题是数学发现的起点和路标;问题具有数学发展的探索和导向作用,可为数学理论的形成积累材料;问题还可以激发人们的创造和进取精神.正如希尔伯特所指出:“只要一门科学分支能提出大量的问题,它就充满着生命力；而问题缺乏则预示着这门科学独立发展的衰亡或中止.数学研究需要自己的问题,正是通过这些问题的解决,研究者锻炼其钢铁意志,发现新方法和新观点,达到更为广阔和自由的境界.”[1]实践中,数学家也总是对所要研究的问题具有强烈的好奇心,倾向于用已有的知识、想象、直觉和推理去解决疑难问题,数学家的本性就是在于发现新的数学,探索新的思想,或者应用已有数学问题去创造发现新的问题.学生应该学会像数学家一样的思维方式,不断地寻求解决问题的方法,并基于已解决的问题提出新的问题.数学教学应当从问题开始,以问题引导数学学习应是数学教学的一条基本原则.一个恰当的富有吸引力的问题,往往能激发学生的认知冲突和探索性思维,培养学生解决问题的能力和学会数学思考的方法,体会数学知识产生和形成的过程,进一步培养学生的创新精神.

数学教学要求以问题作为出发点激发学生的数学学习,尽力让问题充满课堂.没有问题,就很难真正诱发和激起学生对数学的求知欲;没有问题或感觉不到问题的存在,学生就不会深入思考,数学学习也不会有任何收获.所以,应将数学问题作为数学教学的起点、动力和贯穿整个教学过程中的主线,教师应围绕数学问题的创设而安排教学过程.也即是,以提出一个要解决的问题开始,学生需要经历一系列的质疑、判断、比较、选择、分析、综合、归纳、概括等认知活动,伴以个人或小组的数学活动找出不同的可能的解决方案；或由原问题提出新的问题,在解决问题的过程中探索新的概念和方法,进入新的未知的数学领域.如果教师能善于把课堂教学设计成一个又一个生动有趣却又富于思考的问题,激发学生的认知冲突和探索欲望,那么学生就会真正地处于一种积极的思考状态.正如波利亚所指出:“如果教师给他的学生以适合他们程度的问题去引起他们的好奇心,并且用一些吸引人的问题来帮助他们解题,他就会引起学生们对独立思考的兴趣并教给他们一些方法.”[2]研究也表明,基于“问题”学习的学生所取得的成就,无论在标准化测试中还是在解决现实情景的问题测试中,都优于传统的以内容传递为基础的学习环境下所教授的学生.[3]哈尔莫斯也指出:“参加过我的问题课的学生,被后继的教师所赞许.赞许他们灵活的态度,迅速抓住事物核心的能力,以及对问题敏锐探索的本领.”[4]笔者以自己课堂教学实践中亲身经历的一个案例,来谈谈基于“问题”的数学教学及其启示.

案例 如果四边形两组对边延长后分别相交,且交点的连线平行于它的一条对角线,试证另一条对角线的延长线平分对边交点连线的线段.

笔者首先给出这个问题,让学生用数学语言重新表示一下.

学生1：如图1,四边形ABCD中,AB与DC的延长线交于点E,BC与AD的延长线交于点F,且EF∥BD,AC的延长线交EF于点H,AC交BD于点G.

图1

求证:EH=FH.

老师:很好,那我们如何解决这个问题呢?过了一会儿,有一个学生提出了自己的解答.

学生2：

∵BD∥EF，

∴BG=DG,EH=FH.

(同学报以热烈的掌声)

老师:很好,很巧妙的解答!请问同学们还有没有其它不同的解答方法?

图2

学生3 如图2,过点C作CI∥EF,CI交AE于点I,交AF于点J.

∵BD∥EF，

∴S△BDE=S△BDF，

∴S△BCE=S△DCF，即

S△BCI+S△ECI=

S△DCJ+S△FCJ.

又IJ∥BD∥EF，

∴IC=CJ，EH=FH.

(同学又报以热烈的掌声)

老师:很好,又是一个很巧妙的解答!请问同学们还能不能再找到不同的解答方法?

(过了很长时间,学生都没有反应,这时,老师只好自己提示)

老师:要证EH=FH,从全等三角形入手恐怕不适宜,因为图中找不到两个全等的三角形,由BD∥EF，即只要证BG=DG.如何来证BG=DG呢?找全等三角形似乎仍然行不通,也不能用等腰三角形的“三线合一”性质,怎么办呢?

图3

学生4 我们可以运用“平行四边形对角线互相平分”这个性质,来构造一个平行四边形,使得BD为该平行四边形的一条对角线,G为两对角线的交点.因此如图3,可以过点B作BP∥ED,交AC于点P,连接DP.

∵BP∥ED,

又BD∥EF，

∴四边形BCDP为平行四边形,则BD与CP互相平分,即BG=DG. 故EH=FH.

老师:很好,真是不错!请问同学们还能找出其它不同的解法吗?

(学生几乎没有回应,于是,老师又进一步提示)

老师:同学们看着这个图形,再分析已知条件和要求证的结论,你会联想到什么著名的定理?

(学生由于没有学过西瓦定理,一时想不起来,老师只好自己先讲解西瓦定理及其逆定理.然后,提问学生为了能运用西瓦定理,能变更原来问题的表述形式吗？)

学生5：如图1,在△AEF中,ED与BF相交于点C,AC与BD相交于点G,AC的延长线交EF于点H,若BD∥EF，则EH=FH.

又∵BD∥EF，

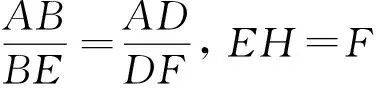
(学生欢呼,真简洁!)

老师:好的,刚才我们已经用了四种不同的方法解决了这个问题,同学们看看能不能就此问题提出新的问题?

(学生一时不明白老师的意思,课堂中一时有些沉闷)

老师继续提示:看看这个问题的已知条件和要求证的结论,结合图形,改变条件和要求证结论的位置关系,看看能否提出新的问题?

学生6：如图1,在△AEF中,ED与BF相交于点C,AC与BD相交于点G,AC的延长线交EF于点H,若EH=FH,则BD∥EF.

数据分析软件使用SPSS18.0，采用均数±标准差表示计量资料，行t检验，X2检验计数资料率，P<0.05时具有统计学意义。

如果一个学生从来就没有机会去解决一个他自己所发明创造的问题,那么他的经验是不完整的.教师要善于引导学生如何从一个刚刚解决的问题引出新问题,这样做可以引起学生的好奇心,让学生进一步体会数学发明创造的过程.

老师:很好,能证明该命题成立吗?

老师:好的,同学们还能不能提出新的问题?

学生7：如图1,在△AEF中,BD∥EF，ED与BF相交于点C,AC与BD相交于点G,点H为EF的中点,求证:A、C、H三点共线.

老师:很好,能证明该命题成立吗?

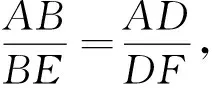
讲到这里,整个课堂气氛非常活跃,学生的情绪处于亢奋和激动之中,大多数学生的脸上露出了兴奋的表情,笔者也深受鼓舞,心里暗自惊叹学生的探索和创造精神!

以上是笔者亲身经历过的一个课堂教学片段,笔者深深感受到基于“问题”的数学教学的强大功能和独特魅力,也力求在课堂中多展现这样的教学片段.这种基于“问题”的数学教学,不仅能使学生对所学知识不断深化,而且能让学生深刻认识到一个问题的各个方面,进而达到深层地认识问题的本质,领悟到数学方法的实质,把学生引入一个完整的领域.正如波利亚所指出:“与其穷于应付繁琐的教学内容和过量的题目,还不如选择一个有意义但又不太复杂的题目去帮助学生深入发掘题目的各个侧面,使学生通过这道题目,就如同通过一道大门而进入一个崭新的天地.”当然,实施这种基于“问题”的数学教学,对教师的素质要求较高,尤其是对教师的数学学科功底提出了较高要求.教师必须深刻理解数学问题的本质(如本案例中四种不同的证法,尤其是第四种证法),教师要能通过设计恰当的“问题”,引导学生学会数学探索.教师要能通过恰当地提问、暗示或补充相关知识(如本案例中补充讲解的西瓦定理及其逆定理),通过搭建恰当的“脚手架”,启发学生获得探究问题的思路与方法(如本案例中的第四种证法和提出的两个新问题).

教师要能按照学生的实际情况,把握好启发的循序渐进性和适时启发性原则.教师对学生探究过程中的错误、存在的困难或产生的偏差不应直接纠正,而是要用另外的补充问题来帮助暴露矛盾(如本案例中的第四种证法),使学生清楚地感到自己的错误、存在的困难或产生的偏差,然后再引导学生获得正确的探究方向或得出正确的结论.教师要善于启发学生去发现问题和提出问题(如本案例中提出的两个新问题),让学生在寻求和探索解决问题的思维活动中,学会数学探究的思维方法和能力.教师要避免将问题单一化、孤立化,应尽可能将所要教授的内容设计为层层相扣的系列问题,引导学生深入思考问题.教师要注意问题设计的多层次和多角度,让学生从多个角度发现问题的答案,思考出问题的多种答案(如本案例中的四种不同证法和提出的两个新问题).如果教师自己没有数学研究(那怕是初等数学研究)的经验,是很难设计和组织这种基于“问题”的数学教学,也很难将问题深入下去并进而提出新的问题(如本案例中提出的两个新问题).

1 [德]希尔伯特著.李文林,袁向东编译.数学问题[M].大连:大连理工大学出版社,2009：38

2 [美]G.波利亚著.阎育苏译.怎样解题(第二版)[M].台北:九章出版社,2000.viii

3 Boaler, J. Open and closed mathematics: student experiences and understandings[J]. Journal for Research on Mathematics Education, 1998, 29(1): 41-62

4 Halmos,P.R. The heart of mathematics[J].American Mathematical Monthly, 1980,87(7 ): 522

教育部人文社科2012年青年基金项目《数学理解的认知科学基础及其应用研究(立项编号:12YJC880131)》.

2015-04-08)