基于hp自适应伪谱法的飞行器再入轨迹优化与制导

夏红伟，李秋实,2，李 莉，宋效正，王常虹

（1. 哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001；2. 中国科学院沈阳自动化研究所，沈阳 110016；3 上海卫星工程研究所，上海 200240）

基于hp自适应伪谱法的飞行器再入轨迹优化与制导

夏红伟1，李秋实1,2，李 莉1，宋效正3，王常虹1

（1. 哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001；2. 中国科学院沈阳自动化研究所，沈阳 110016；3 上海卫星工程研究所，上海 200240）

研究了一种基于hp自适应伪谱法的飞行器再入在线轨迹优化与制导方法。首先针对飞行器再入段在末速度最大的条件约束下进行了轨迹优化；然后针对再入段地球大气分布不均匀、建模误差、扰动等因素，设计了基于hp自适应伪谱法的反馈制导方法；最后进行了数学仿真研究。仿真结果表明：采用本文提出的反馈制导方法得到的末速度为6.93 km/s，比未采用闭环制导的方法提高了0.33 km/s，并且制导精度提高了15倍。

飞行器再入；hp自适应伪谱法；轨迹优化；反馈制导

返回、再入和着陆过程是返回式航天器整个飞行任务链的最后阶段，保证航天器安全再入返回是航天技术研究的重要问题。其中再入段由于经过大气层，动力学模型相对复杂，并且由于存在建模误差、各种扰动等因素，该阶段的轨迹优化和制导设计显得尤为重要[1-4]。

Naidu[5]采用匹配渐近展开法基于ADBARV坐标系的大气层内飞行器动力学方程对飞行器再入优化问题进行了求解分析。Zimmerman等[6]提出了一种用于可重复使用飞行器再入阶段的控制算法，借助自主仿真和自寻的技术解决飞行器再入问题。目前对于飞行器再入段动力学模型的研究已经取得了较好的研究成果，但在再入段轨迹优化方法方面，普遍存在最优轨迹生成时间长的困扰[6-7]；由于轨迹生成时间长，多采用离线生成最优轨迹进行制导，这导致制导精度受模型参数变化、扰动等因素影响而难以提高[1-3,8-9]。针对上述问题，本文采用hp自适应伪谱法对飞行器再入段进行轨迹优化，并设计了一种在线轨迹生成的hp自适应伪谱法反馈制导法，通过仿真验证了方法的可行性。

1 飞行器再入段建模

与载人飞行器的再入过程不同，本文研究的飞行器再入过程以保持高速下降为目标，其下降时间极短，故可对再入段做如下假设：1）地球为匀质圆球且不考虑自转；2）忽略地球大气与地面的相对运动，且同高度分布均匀；3）再入飞行器质量不变。飞行器在大气层内的运动受重力和气动力的综合作用，选取位置幅值R、速度幅值V、赤经θ、地心赤纬λ、航迹角γ、偏航角ψ作为状态量。飞行器模型可描述为式(1)所示：

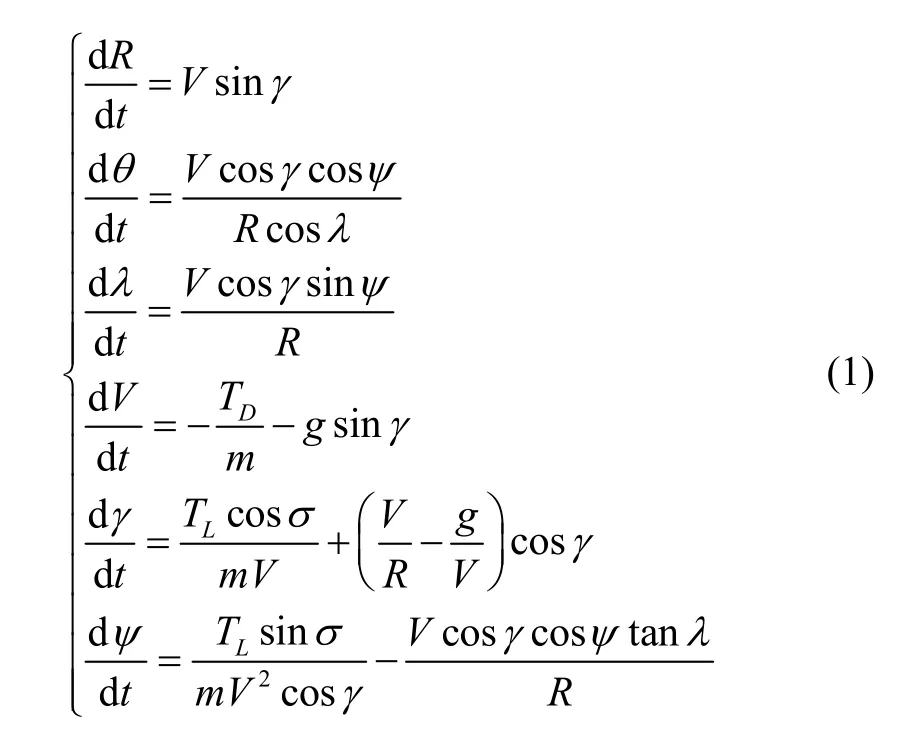
式中，m为飞行器质量，σ为倾侧角，TD、TL分别为阻力和升力，可由式(2)表示：

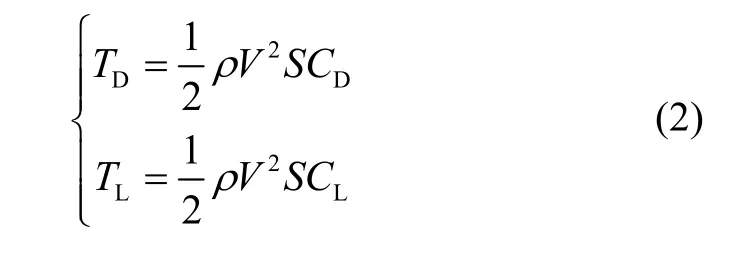
式中：ρ为大气密度，S为飞行器有效面积；CD、CL分别为阻力系数和升力系数，这两个系数决定了气动模型的精确程度。为保证模型精度，本文采用文献[8]中通过高精度的拟合得到的阻力和升力系数模型，如式(3)所示：

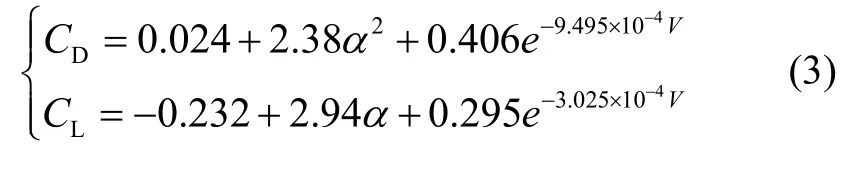
由上面模型可见，飞行器再入段的运动轨迹由攻角α和倾侧角σ这两个控制量确定。

对于本文研究的飞行器再入问题，该模型可以进一步简化成式(4)形式：

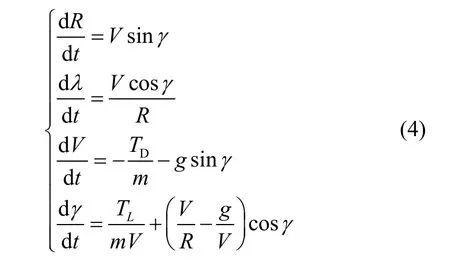
此时，λ代表再入飞行器航程对应的地心角，飞行器再入段的运动轨迹由攻角α控制。

2 轨迹优化方法分析

轨迹优化方法可分为间接法和直接法。近年来，由于直接法具有对初值依赖小、收敛速度快的优点，取代间接法成为了发展主流。直接法直接对动力学方程和控制量进行离散化，将轨道的优化转化为一个参数优化问题，并利用参数优化方法求解问题从而得到最优轨迹。伪谱法是一种优秀的直接轨迹优化方法，它采用全局插值多项式为基函数，近似整个时间历程的状态变量和控制变量。它可采用较少的离散点得到极高精度的拟合近似解。一般拟谱法的拟合精度为节点数的指数精度，要远远高于其他直接法的精度。但在处理一些模型复杂的最优控制问题时，伪谱法中插值多项式阶数过高会导致雅克比矩阵及海森矩阵维数过高，运算难以进行[9]。

此外，有限元法是一种通过对连续体离散化求解力学问题的数值计算方法，它提高计算精度的方法可分为h细化和p细化。其中，h细化是对插值单元长度h进行细分，即通过加密有限元网格以提高精度；p细化是提高插值多项式的阶数p以提高精度。hp型有限元法同时并独立的采用h细化和p细化两种提高精度方法，从而可以在合理的网格密度和插值多项式阶数的情况下获得较高精度。

hp自适应伪谱法就是将有限元法思想和全局伪谱法相结合得到的最优控制方法。通过hp型有限元法的思想自适应的选取时间区段数和插值多项式阶数，在较低运算代价的情况下获取较高的精度。本文所研究的飞行器再入段经过大气层，动力学模型较为复杂，鉴于此，本文采用hp自适应伪谱法，将有限元法中的细化思想引入伪谱法中，可有效提升伪谱法的运算效率[7-10]。

2.1 伪谱法基本原理

hp自适应伪谱法与全局伪谱法在参数离散化方面原理相同，下面通过全局伪谱法中典型的Gauss伪谱法说明伪谱法的基本原理：

① 典型的最优控制问题典型的最优控制问题在时间区间上单位化可表述为：已知系统状态变量x(τ)∈ Rn，控制变量u(τ)∈ Rm，性能指标为

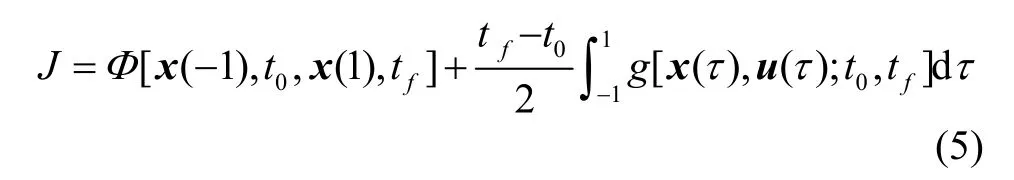
状态约束f、路径约束C和终端约束Φ：

② 插值节点选择和变量离散化插值节点选择为Legendre-Gauss节点：

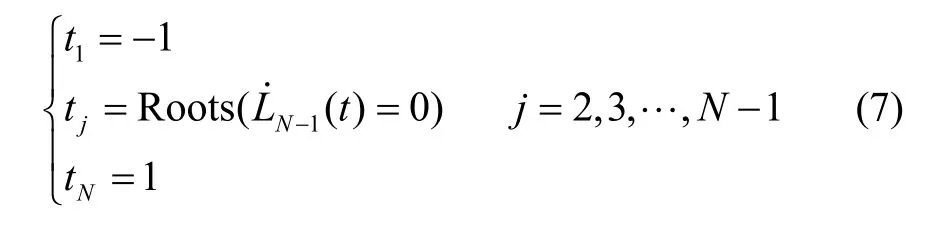
式中，LN-1(t)为Legendre多项式。Legendre多项式如式(8)所示：

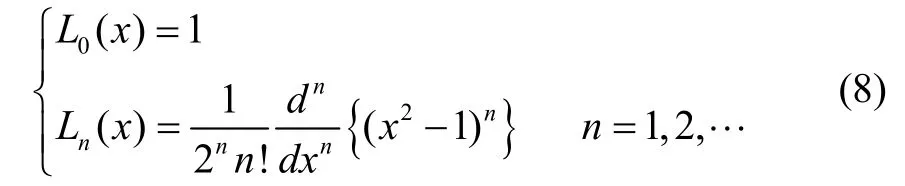
采用Legendre-Gauss节点对状态变量xtj和控制变量utj离散化：

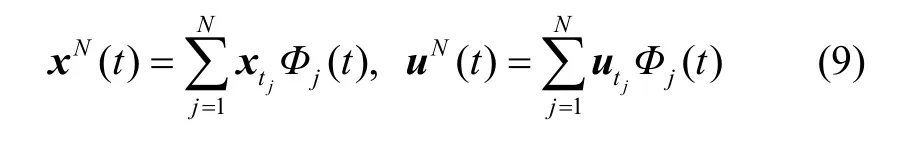
式(9)中Φj(t)即为Lagrange插值多项式：

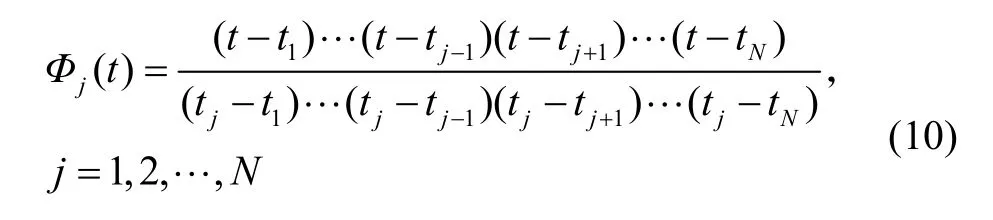
③ 离散化后的最优控制问题

离散化后，状态方程可近似表示成如下代数方程：

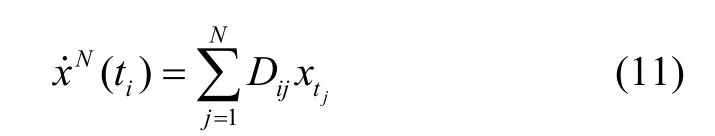
式中的Dij即为拟谱法差分矩阵：

约束条件和最优指标均可用节点处的值表示，其中状态约束为

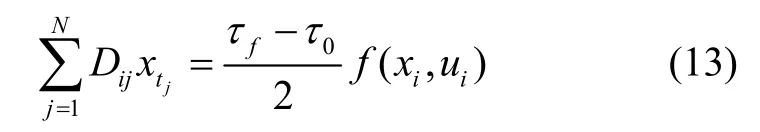
终端约束和路径约束为

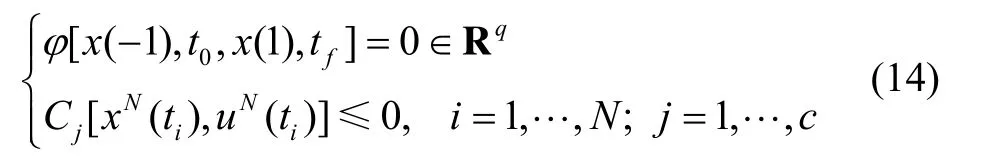
性能指标为

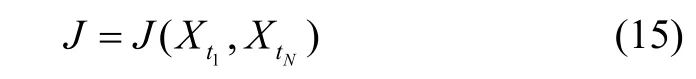
至此，原最优控制问题就转化成了非线性规划问题，可以利用SNOPT算法对其进行求解。

2.2 hp网格细化方法

hp网格细化方法是一种在保证运算复杂度在可控范围内提升伪谱法精度的方法[9]。在hp伪谱法中，最优控制问题在 t∈[t0, tf]上分为 H 个时间区间，h∈[1,2,…,H]对应时间区间[th-1, th]。然后对每个时间区间进行离散化，设每个时间区间节点数为Ph。hp网格细化方法就是通过确定时间区间数H和节点数Ph是否需要增加达到优化伪谱法的目的。

对于H和Ph的调整由每两个节点间中点对状态约束的满足程度决定，各中点为

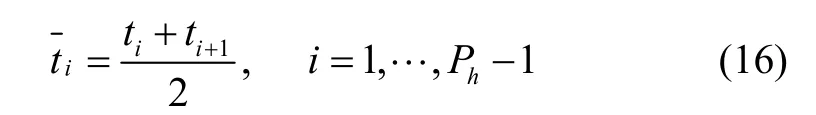
通过对状态约束式(13)进行变换可得中点残差矩阵为

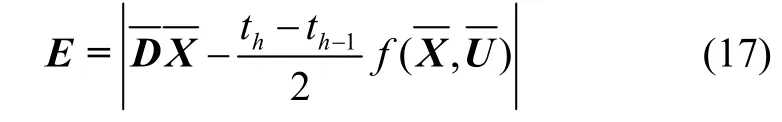
式(17)中绝对值符号表示对矩阵中每个元素求绝对值。对E中每一行取最大元素，组成列向量如下：

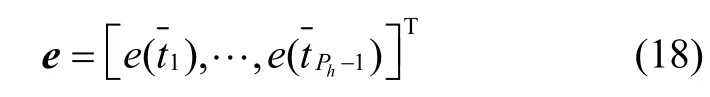
定义：

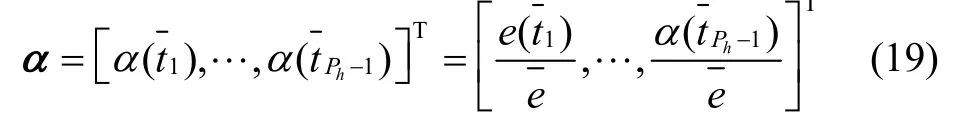
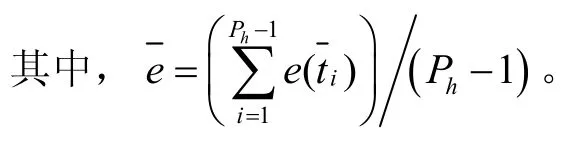
此时可以通过向量α确定优化方案。若向量α中所有元素均处于相同数量级，则可进行p细化，即通过增加节点数提高整体精度；若向量α中部分元素数量级远高于其他元素，则需对这些元素对应的时间区段采用h细化，通过进一步细化时间区段提高精度。

3 hp自适应伪谱法反馈制导

飞行器制导问题是典型的最优控制问题，可表述如下：

状态方程：

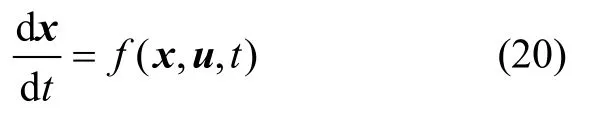
性能指标：

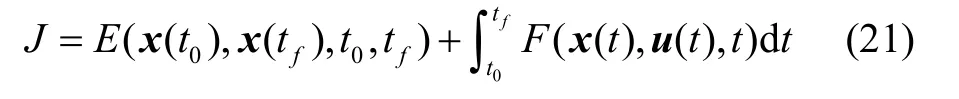
约束条件：

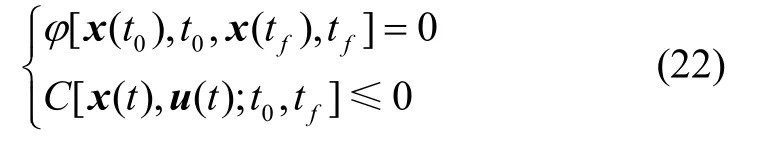
反馈制导实质就是建立由状态变量x和时间t至控制变量u的映射：

解决此类问题的传统方法是通过动态规划理论或Pontryagin极小值原理进行求解。但对于飞行器制导问题，往往由于模型复杂无法得到连续的反馈控制率。此时的解决方案就是求取不连续的反馈控制率。当反馈控制率为不连续时，状态方程(20)也为不连续的，此时的状态方程解为Carathéodory解[10]。

假设对动力学系统(20)采用时不变反馈控制ĝ(x)。取π={ti}∈[0,∞), i=0,1,…,π的直径为diam(π)= sup(ti+1-ti)。取x0作为初始值，对于时不变反馈控制函数ĝ(x)，π解定义为：

首先在[t0, t1]上求下面状态方程的解：

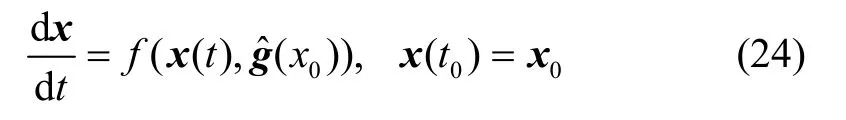
然后取初值为x1，在[t1,t2]上求下面状态方程的解：

按上面方式类推下去，即可得到各时间段开环制导率。将各个时间段合在一起即可得到闭环制导率，合在一起的解也就是π解。

以上即为当前常见制导方法的原理。显然，当diam(π)→0时闭环制导率为理想制导率，但由于制导周期的限制，常见制导方法无法达到此理想情况。当前常用的制导方法通常是设定一个所能达到的制导周期，在制导周期开始时计算最优控制量，然后在整个制导周期将此值作用于飞行器，在下一个制导周期再计算新的控制量。

其制导方法流程可以表示为图1所示[9]。首先根据任务目标求解离线最优轨迹，通过最优轨迹确定控制量的变化规律，形成制导算法。飞行器实际运行时，由于受到扰动作用会偏离离线确定的最优轨迹，将由测量系统得到的实际运行轨道参数与最优轨迹相对比，通过偏差值确定控制量，在每一制导周期控制量通常不变，并且由于最优轨线为飞行器工作前离线生成，无法在实际飞行过程通过具体情况调整，采用此种制导方法往往会导致真实制导精度很低。

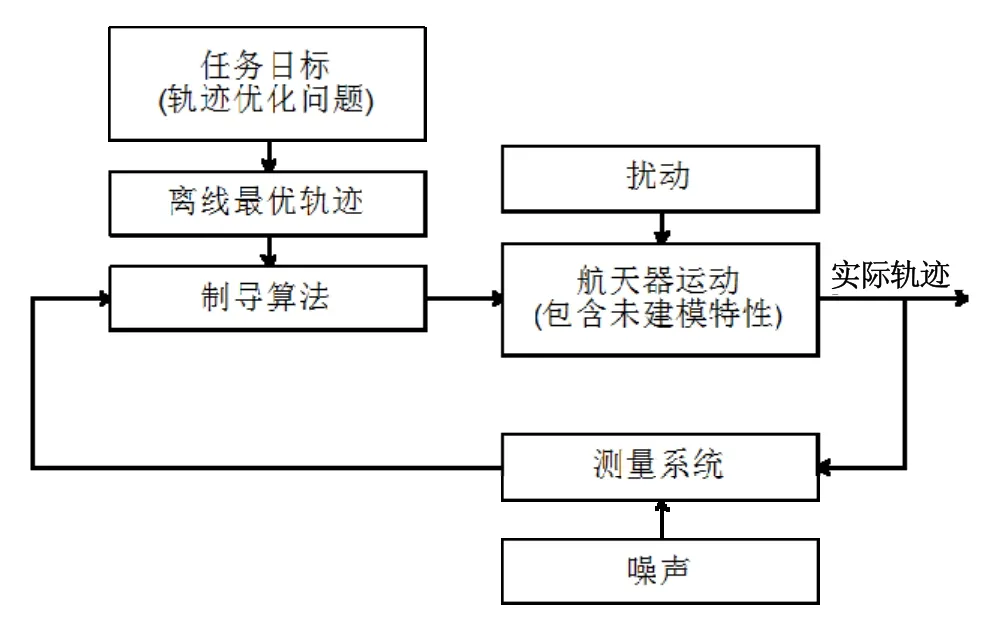
图1 当前常见的制导方法流程Fig.1 Flowchart of current common guidance method

鉴于此，本文基于hp自适应伪谱法反馈制导实现“时变制导”，不同于当前常见的制导方法，hp自适应伪谱法反馈制导法采用时变控制率g(x,t)。为求解此时的状态方程我们需引入新的变量，满足

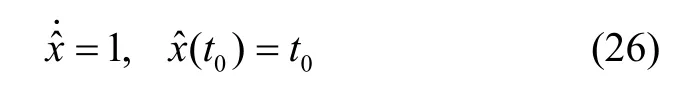
此时状态方程为

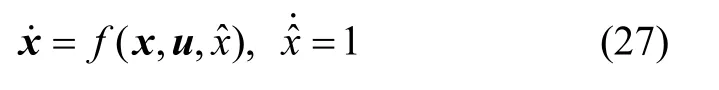
至此，可以仍采用前面的分时间段方法解此状态方程，得到各时间段开环制导率，将各个时间段合在一起得到闭环制导率。

上述就是hp自适应伪谱法反馈制导的基本原理，与当前常用伪谱法同样是采用分时间段的方式，但不同的是制导周期内控制量会发生变化，不同制导周期控制策略也会发生变化，从而提高了制导精度。

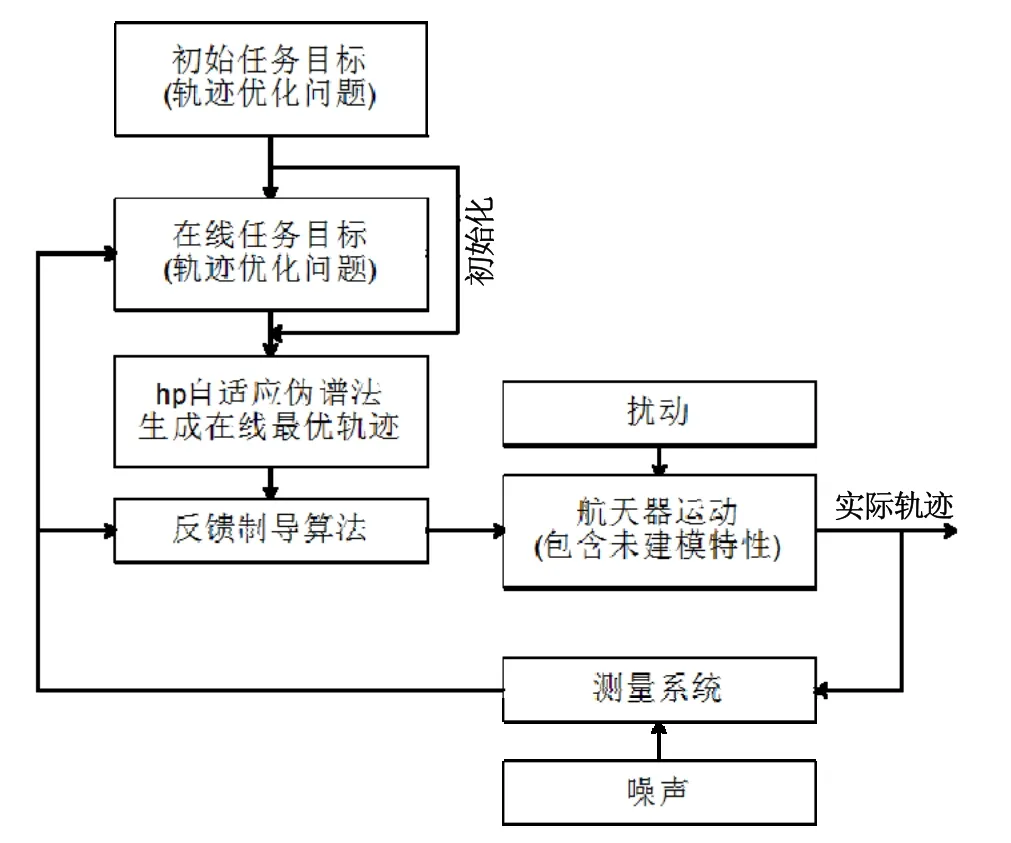
图2 hp自适应伪谱法反馈制导流程Fig.2 Feedback control process of hp-adaptive pseudospectral method

hp自适应伪谱法反馈制导流程如图2所示。首先针对初始任务目标求取初始最优轨迹并生成制导算法，控制飞行器运行；然后将由测量系统得到的实际运行轨道参数用于更新任务目标，在线生成新的最优轨迹，并且更新制导算法，采用新的制导算法来控制飞行器在新的制导周期内运行。由于采用了在线实时更新制导率的方式，hp自适应伪谱法反馈制导使飞行器对扰动和模型变化的适应能力大幅提升。

4 仿真分析

4.1 飞行器再入段轨迹优化

对于本文研究的飞行器再入飞行任务，假设飞行着陆平面垂直于经线，平面动力学模型采用式(4)所示简化的气动力方程即可。并且，本文研究的飞行任务要求飞行器在到达地面后具有较大的速度，故以飞行器到达地面速度最大作为最优指标，约束条件为初始参数和终端位置。综上所述，该轨迹优化问题可表述为

性能指标：

状态方程：

约束条件：

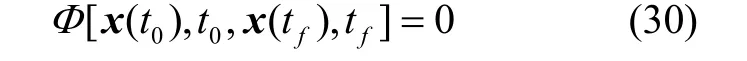
采用前文研究的 hp自适应伪谱法对此最优控制问题进行求解，通过MATLAB中的SNOPT工具包进行优化计算。仿真初始参数设置如表1所示，目标纬度设为51.4°。

表1 初始参数设置Tab.1 Settings of Initial parameters

仿真结果如图3～5所示。图3为最优轨迹对应控制量攻角α的变化情况，可见，在攻角在较小范围内变化的情况下即可实现最优轨迹。图4为最优轨迹示意图，可见最优轨迹在占大部分时间的前半段近似于倾斜的直线，后期迅速下降近乎垂直落地。图5为最优轨迹对应各状态变量变化情况，可见，高度和纬度变化比较平缓，速度和路径角前期变化较小，接近地面时由于大气密度的增大变化较大。

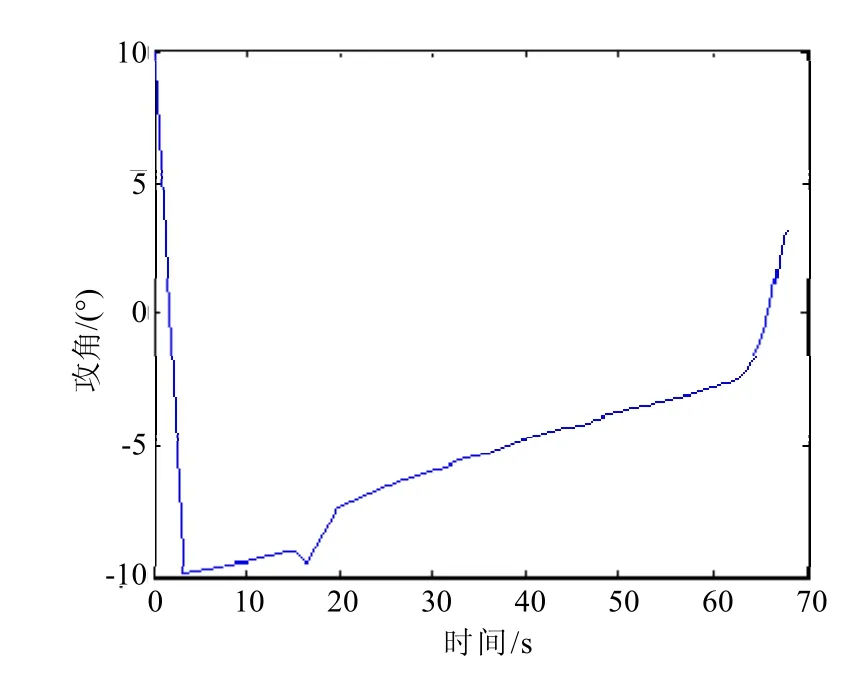
图3 最优轨迹对应攻角变化曲线Fig.3 Angle of attack of optimal trajectory

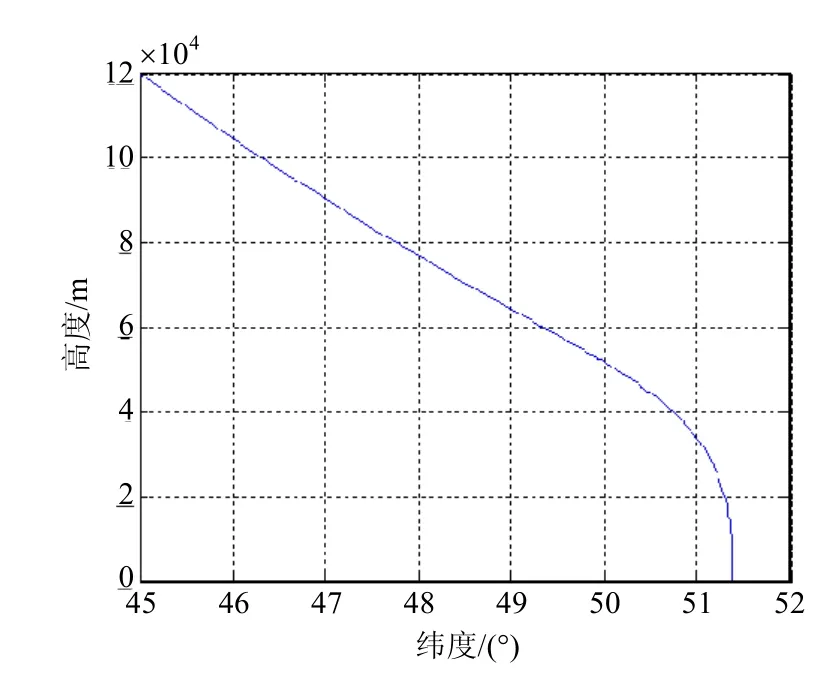
图4 飞行器再入段最优轨迹Fig.4 Optimal trajectory of craft reentry

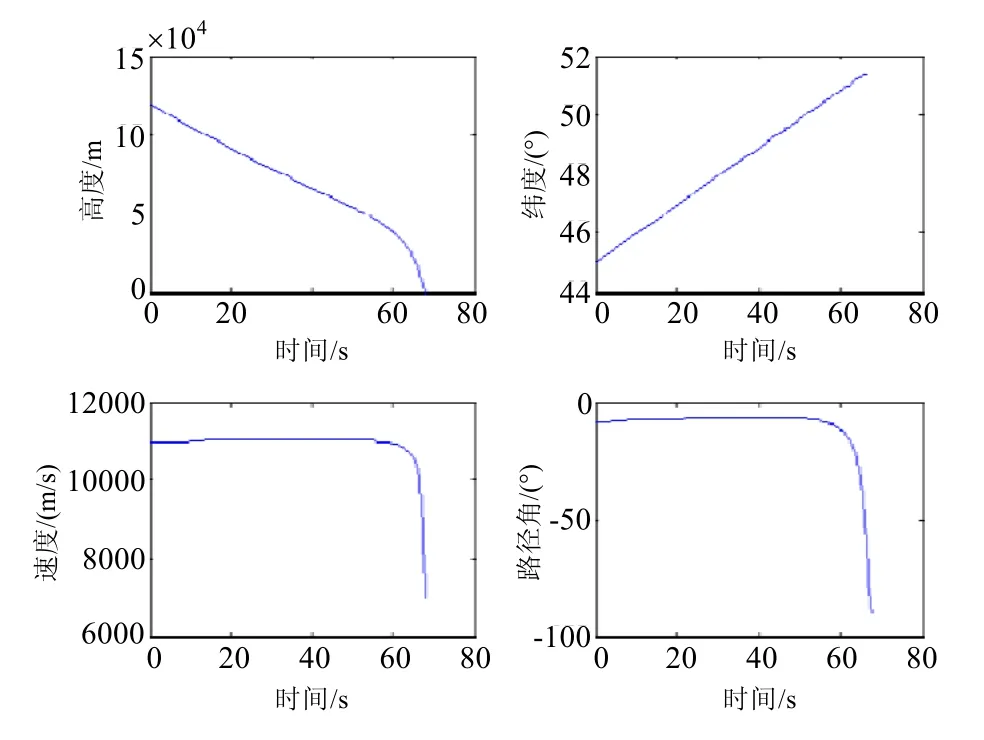
图5 最优轨迹对应状态量变化曲线Fig.5 State variables according to optimal trajectory

4.2 飞行器再入段制导

由于存在地球大气分布不均匀、建模误差、扰动等因素，若控制量采用预先计算的值，飞行器再入过程往往会偏离最优轨迹，本部分采用hp自适应伪谱法反馈制导对该过程进行制导设计。

仿真参数与 4.1节相同，并加入大气模型变化，仿真结果如图6至图8所示。本次仿真输出了离线计算的最优轨迹和采用 hp自适应伪谱法反馈制导的飞行器实际运行轨迹，并加入未采用闭环制导方法的飞行器实际运行轨迹作为对比。

图6为速度随时间变化示意图。如图6所示：离线计算的末速度约为7 km/s，而未采用闭环制导的实际运行末速度仅为6.6 km/s；而采用hp自适应伪谱法反馈制导的末速度为6.93 km/s，与最优值很接近。

图7为飞行器再入段纬度随时间变化图，图8为飞行器再入段轨迹，二者均可判定制导位置精度。从两图均可看出，离线最优轨迹（即设计轨迹）落点为51.4°，而未采用闭环制导的实际轨迹落点纬度值小于51.38°，与设计落点有较大偏差。而采用hp自适应伪谱法反馈制导的实际轨迹落点为51.397°，与预定落点仅有0.003°的偏差，着陆精度大约300 m。这个精度对于对类似战略打击、太空救援等任务已经足够了。

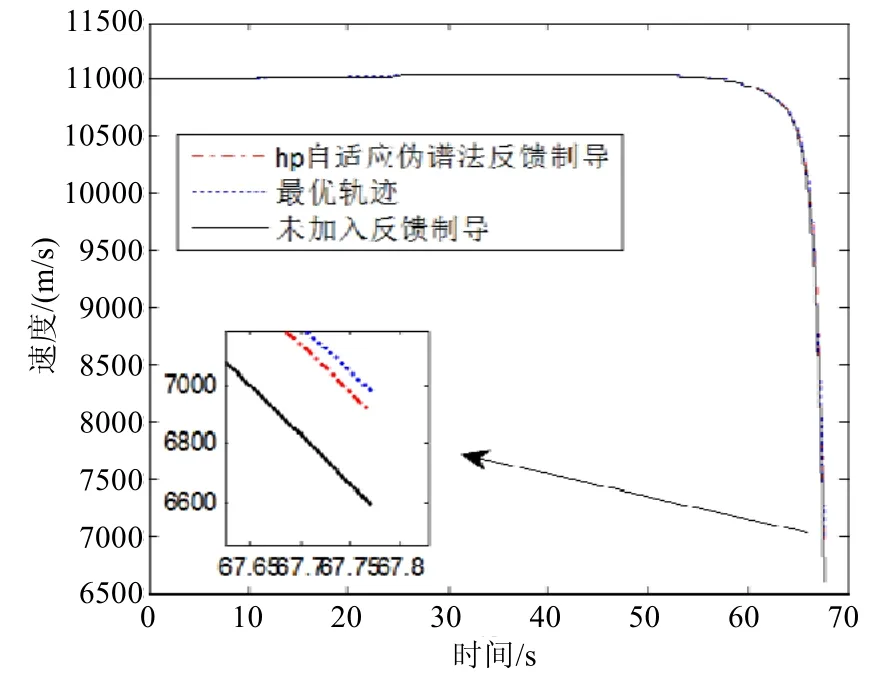
图6 飞行器再入段速度随时间变化示意图Fig.6 Velocity of craft reentry

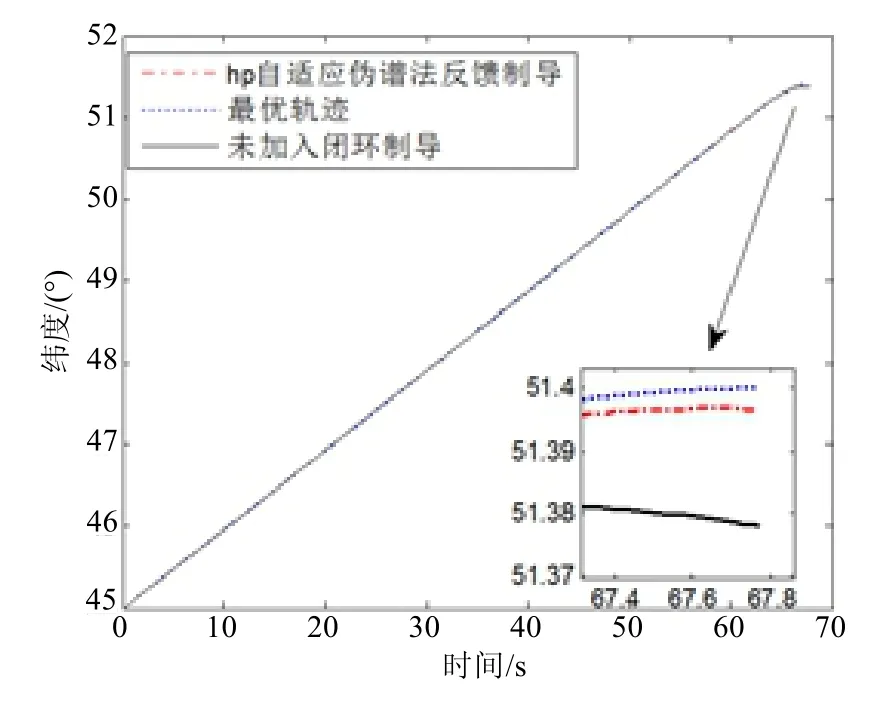
图7 飞行器再入段纬度随时间变化示意图Fig.7 Latitude of craft reentry

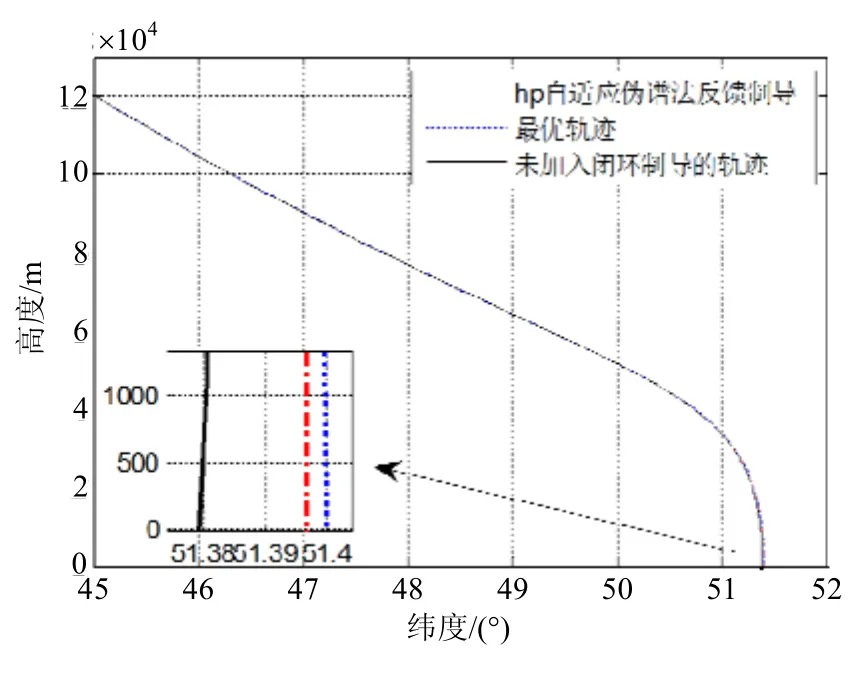
图8 飞行器再入段轨迹示意图Fig.8 Trajectory of craft reentry

5 结 论

本文采用 hp自适应伪谱法对飞行器再入问题进行了轨迹优化设计与制导方法的研究，根据任务特点设定末速度最大为优化目标。针对飞行器再入段存在地球大气分布不均匀、建模误差、扰动等因素的问题，提出了一种基于hp自适应伪谱法解决飞行器再入段的制导设计方法，实现了在线反馈制导率的设计，并通过MATLAB仿真验证了该制导方法的可行性和优越性。

（References）：

[1] Nan Ying, Lu Yu-ping, Gong Ping. Optimal reentry trajectory design for mooncraft returning to the earth[J]. Journal of Astronautics, 2009, 5: 015.

[2] Zhang, Ke-nan, Chen Wan-chun. Reentry vehicle constrained trajectory optimization[C]//Proceedings of the AIAA International Space Planes and Hypersonic Systems and Technologies Conference. 2011.

[3] 李强, 夏群利, 郭涛, 等. 一种基于解析规划的多约束再入制导算法[J]. 弹箭与制导学报, 2013, 33(1): 1-4, 9. Li Qiang, Xia Qun-li, Guo Tao, et al. Reentry guidance research with multi-constrain based on analytic planning method[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(1): 1 - 4, 9.

[4] 胡正东, 郭才发, 蔡洪. 天基对地打击动能武器再入解析预测制导技术[J]. 宇航学报, 2009, 21(15): 1039-1044. Hu Zheng-dong, Guo Cai-fa, Cai Hong. Analytical predictive guidance for space-to-ground kinetic weapon in reentry[J]. Journal of Astronautics, 2009, 21(15): 1039-1044.

[5] Naidu D. Three-dimensional atmospheric entry problem using method of matched asympotic expansions[J]. IEEE Transaction on Aerospace and Electronic Systems, 1989, 1(11): 660-667.

[6] Zimmerman C, Dukeman G, Hanson J. Automated method to compute orbital reentry trajectories with heating constraints[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 523-529.

[7] Xie Yu, Liu Lu-hua, Tang Guo-jian, et al. A reentry trajectory planning approach satisfying waypoint and nofly zone constraints[C]//5th International Conference on Recent Advances in Space Technologies, 2011: 241-246.

[8] 王光伦. 高超声速飞行器再入段预测校正制导研究[D].哈尔滨: 哈尔滨工业大学, 2010. Wang Guang-lun. Study on reentry guidance algorithm of space-based hypersonic vehicle[D]. Harbin: Harbin Institute of Technology, 2010.

[9] 洪蓓, 辛万青. hp自适应伪谱法在滑翔弹道快速优化中的应用[J]. 计算机测量与控制, 2012, 20(5): 1283-1286. Hong Pei, Xin Wan-qing. Application of hp-adaptive pseudospectral method in rapid gliding trajectory optimization[J]. Computer Measurement & Control, 2012, 20(5): 1283-1286.

[10] Ross I M, Sekhavat P, Fleming A, Gong Q. Pseudospectral feedback control: foundations, examples and experimental results[C]//AIAA Guidance, Navigation, and Control Conference Exhibit. Keystone, Colorado, 2006: 1-23.

Trajectory optimization and guidance for reentry craft based on hp-adaptive pseudospectral method

XIA Hong-wei1, LI Qiu-shi1,2, LI Li1, SONG Xiao-zheng3, WANG Chang-hong1
(1. Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China; 2. Shenyang Institute of Automation Chinese Academy of Sciences, Shenyang 110016, China; 3. Shanghai Institute of Satellite Engineering, Shanghai 200240, China)

An online optimization and guidance approach for craft reentry trajectory is presented based on hp-adaptive pseudospectral method, in which the trajectory of craft reentry phrase is optimized in condition of maximum final speed. In view that the atmospheric model of reentry phase is irregular, and the spacecraft always encounter disturbance and is difficult to get an accurate model, a feedback control algorithm is derived based on the hp-adaptive pseudospectral method. Simulations are made, which demonstrate that the final-speed got by our approach is 6.93 km/s, which is 0.33 km/s higher than those without closed-loop-guidance, and the guidance precision is improved by 15 times, showing the effectiveness of the proposed approach.

craft reentry; hp-adaptive pseudospectral method; trajectory optimization; feedback guide

V448.2

：A

2015-08-11；

：2015-11-20

国家自然科学基金（61304108）；上海航天科技创新基金资助项目；CAST创新基金项目

夏红伟（1979—），男，博士，主要从事飞行器控制及仿真技术方面的研究。E-mail: xiahongwei@hit.edu.cn

联 系 人：王常虹（1961—），男，教授，博士生导师，主要研究方向为导航、制导与控制。E-mail: cwang@hit.edu.cn.

1005-6734(2015)06-0818-06

10.13695/j.cnki.12-1222/o3.2015.06.021