双质量解耦硅微陀螺仪的非理想解耦特性研究和性能测试

杨 波，吴 磊，周 浩，胡 迪，刘显学

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3. 中国工程物理研究院电子工程研究所，绵阳 621999）

双质量解耦硅微陀螺仪的非理想解耦特性研究和性能测试

杨 波1,2，吴 磊1,2，周 浩3，胡 迪1,2，刘显学3

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3. 中国工程物理研究院电子工程研究所，绵阳 621999）

为了分析双质量解耦硅微陀螺结构中的机械耦合误差，对微陀螺结构的非理想解耦特性进行了研究。首先，阐述了双质量解耦硅微陀螺仪的结构原理，推导了双质量解耦硅微陀螺仪的检测位移；接着构建检测框架在驱动模态下非理想的解耦模型，推导了由非理想解耦导致检测框架的平动位移与转动位移的公式；然后进行了结构非理想解耦特性仿真分析，对驱动模态时检测框架和检测模态时驱动框架的非理想运动特性进行仿真，结果表明检测框架的残余平动位移达到驱动位移的0.86%，最大转动残余位移达到了驱动位移的2.7%， 而驱动框架的平动残余位移达到了检测位移的1.36%，转动残余位移达到了检测位移的0.87%；最后，对加工的双质量解耦硅微陀螺结构芯片的非理想解耦误差进行了测量，结果表明非真空封装下的正交误差达到158.65 (º)/s，失调误差为19.03 (º)/s，偏置稳定性达到12.01 (º)/h。

硅微陀螺仪；双质量；非理想解耦；非真空封装

硅微陀螺仪是一种基于 MEMS技术的微惯性传感器，已经过二十多年的研究发展[1-3]。硅微陀螺仪最初结构以单质量居多，但是单质量硅微陀螺结构在敏感轴方向无法区分线性加速度干扰与输入哥氏加速度。为了抑制敏感轴向加速度或振动的影响，诸多机构开展了双质量硅微陀螺仪研究[4-5]。在硅微陀螺仪早期结构中，驱动和检测方向是全耦合的，质量块既沿着驱动方向运动，又沿着检测方向运动，极易导致两个模态间的机械耦合。为了抑制两模态间的机械耦合，解耦技术被引入硅微陀螺仪的结构设计，先后出现了半解耦和全解耦硅微陀螺仪结构[6-7]。最近，随着硅微陀螺仪的研究进步，结合上述两种技术的双质量全解耦硅微陀螺结构成为研究热点[8-9]。全解耦技术在理论上可以完全抑制两模态间的机械耦合误差，但是由于现实中无法获得完全理想的解耦梁，很难实现理想解耦。因此，本文对课题组设计的双质量全解耦硅微陀螺仪的非理想解耦特性进行分析、仿真和试验。

1 双质量解耦硅微陀螺仪结构原理

双质量解耦硅微陀螺仪的原理如图1所示。整个结构由两个完全相同的单质量陀螺仪构成，并左右对称放置。每个单质量陀螺仪由质量块、驱动框架、驱动电极、驱动敏感电极、检测框架、检测电极、反馈电极、驱动悬臂梁、检测悬臂梁、驱动解耦梁、检测解耦梁和锚点组成。在驱动方向上，两个单质量陀螺仪通过驱动耦合悬臂梁实现驱动模态的耦合；在检测方向上，两个单质量陀螺仪通过敏感耦合悬臂梁和耦合横梁实现检测模态的耦合。当在驱动电极上施加驱动力时，由于敏感解耦梁在驱动方向刚度很大，驱动框架将通过敏感解耦梁推动两个质量块反向振动，而驱动解耦梁由于在驱动方向的刚度较小，因此敏感框架在驱动方向基本保持不动，实现了驱动解耦；当沿着z轴有角速度输出时，由于驱动解耦梁在检测方向刚度较大，两个质量块在哥氏力作用下，将通过驱动解耦梁推动敏感框架做反相运动，由于敏感解耦梁在检测方向刚度较小，因此驱动框架将在检测方向基本保持不动，实现了检测解耦。该双质量解耦陀螺具有以下特点：

① 大量采用 U型梁形式，使力与位移的线性关系，结构振动平稳；

② 驱动机构和驱动检测机构采用变面积滑膜梳齿，空气阻尼小，品质因数高，适合非真空工作；

③ 整个陀螺结构采用全解耦结构形式，能有效地减少机械耦合误差；

④ 两个单质量陀螺仪完全相同并左右对称放置，实现差分检测，提高了硅微陀螺仪共模误差抑制能力和信噪比。

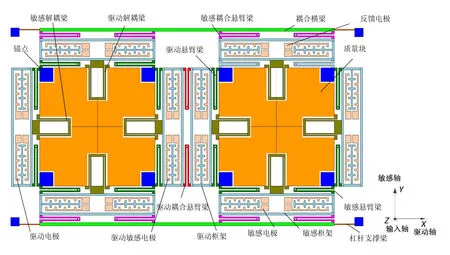
图1 双质量全解耦硅微陀螺仪的结构原理图Fig.1 Structure scheme of the decoupled dual-mass micro-gyroscope

2 非理想解耦特性分析

图2为检测模态的等效模型，由于驱动模态和检测模态类似，驱动模态可以采用类似方法分析。图中ml和mr是左右质量块的质量，mdyl和mdyr是左右检测框架的质量，ky是检测机构的刚度，cyl和cyr是左右检测机构的阻尼，kyo是耦合刚度，Fc1和Fc2是左右机构的哥氏驱动力。则检测系统方程为

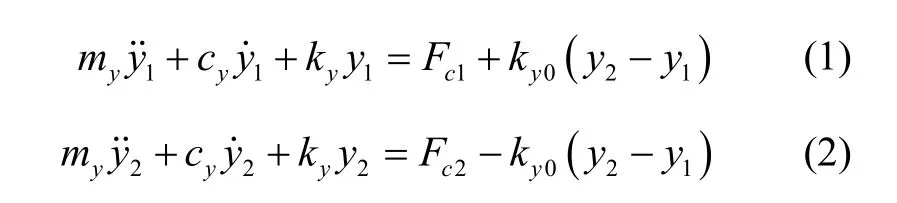
假设my=ml+mdyl=mr+mdyr，cy=cyl=cyr，且驱动位移为x=x1=-x2=Hsinωx2t，ωx2为反相驱动频率 Fc1=-Fc2= 2myΩωx2Hcosωx2t，Ω为输入角速度，则两质量块检测位移为

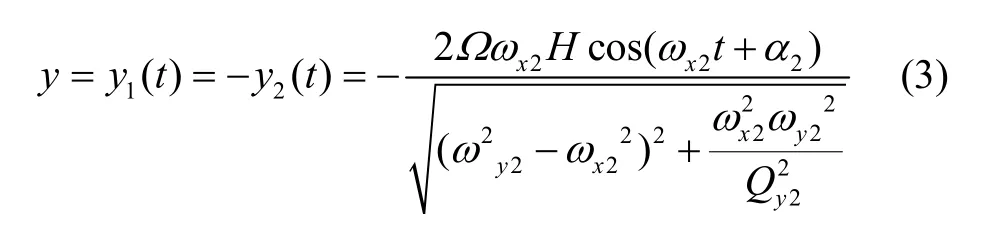
式中，ω2y2=(ky+2kyo)/my为反相敏感谐振频率，Qy2= ωy2my/cy为品质因数。

当上述双质量全解耦硅微陀螺仪的两个结构反相驱动时，如果结构的解耦是理想的，即驱动解耦梁在驱动方向（x方向）的刚度趋近于零，而在检测方向（y方向）的刚度趋近与于无穷大，则检测框架将不会有位移。但是由于驱动解耦梁在驱动方向存在一定的刚度，将导致部分驱动力会传递到检测框架，如图3(a)所示。同样，由于图3(a)中的敏感耦合悬臂梁和敏感悬臂梁在检测方向（y方向）的刚度有限（不是趋近无穷大），传递过来的驱动力将会导致耦合的平动和转动位移。检测框架在x方向的简化受力模型，如图3(b)所示。

根据图3(b)的模型建立系统的平衡方程：

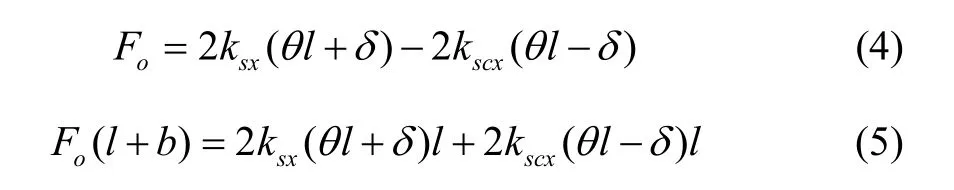
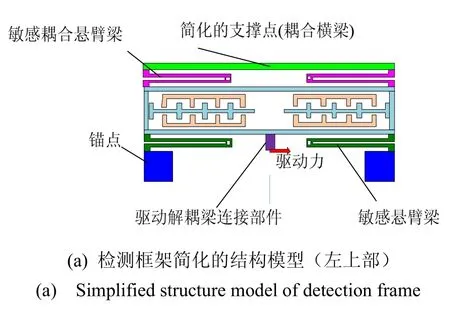
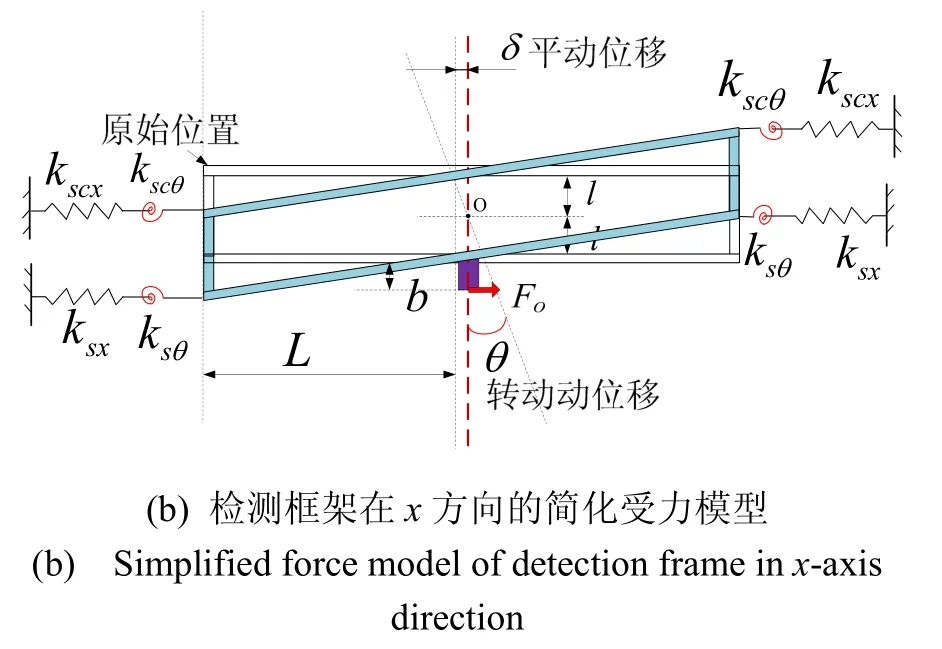
图3 驱动模态时检测框架受力分析Fig.3 Stress analysis of detection frame in drive mode

解方程得：

假设单根驱动解耦梁在x方向的刚度为kddx，则：

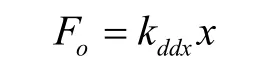
根据式(6)和式(7)，得残余解耦位移与驱动位移的比值为

式(8)为 x方向的平动位移与驱动位移的比值，式(9)为沿着 y方向的转动位移与驱动位移的比值，式(10)为敏感耦合悬臂梁在两个方向的刚度比，N为梁长度，E为转折部分的长度。因此，为了减小残余解耦位移，可以将敏感耦合悬臂梁和敏感悬臂梁结构参数设计尽可能靠近，即kscx≈ksx，同时可以在不改进结构模态特性情况下，增大敏感悬臂梁和敏感耦合悬臂梁在 x方向刚度ksx、kscx（即增加N，减小E），或减小驱动解耦梁在x方向的刚度kddx。

非理想的解耦特性导致检测框架产生一种平动和转动相结合的耦合运动。整个检测梳齿作为一个电容信号器，是一个沿着y轴方向的滑膜梳齿，左右梳齿间隙相等，对x方向的平动位移有较好的抑制作用。同时在一组检测框架内，检测梳齿左右对称布置，对转动位移也具有一定的抑制效果。但是由于加工误差的存在，仍然会有一定残余误差，并且由于耦合的平动和转动位移较大，其残余误差不可忽略。整个检测梳齿总体耦合位移可以表示为

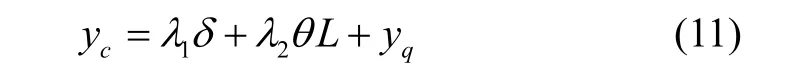
式中：λ1和 λ2分别为平动和转动误差抑制系数；yq为由于加工误差等引起沿着y方向耦合力导致误差位移，该位移在以前文献中有诸多论述，不在详述[10]。以上三种误差是信号通道中主要共模误差，测试中很难区分，只能进行整体测量。

不考虑yq的影响，则非理想解耦误差位移与检测位移的比值的模为

类似的情况，在检测模态，如果结构的解耦是理想的，即敏感解耦梁在检测方向（y方向）的刚度趋近于零，而在驱动方向（x方向）的刚度趋近与于无穷大，则驱动框架将不会有位移。但是由于敏感解耦梁在敏感方向存在一定的刚度，将导致部分敏感力会传递到驱动框架上。

3 结构非理想解耦特性仿真

为了进一步验证非理想解耦特性，利用Ansys软件构建了双质量解耦硅微陀螺仪的仿真模型，且利用该模型对非理想的解耦特性进行了仿真。图4 和图5为驱动模态和检测模态的非理想解耦特性仿真结果。其中图 4(a)为驱动模态，两个质量块反相运动，并且驱动框架和质量块在驱动方向运动明显，而检测框架运动微弱，达到了一定的解耦特性。图4(b)为检测框架放大图，可见解耦后检测框架有一定的残余运动，表现为平动与转动结合运动特性。为了分析残余运动特性，对检测框架中心线上的A、B、C和质量块中心在x轴和y轴方向的位移进行了分解，如表1所示。 由表中的数据可见，A、B、C三点在x轴方向的位移基本相等，显示显著的平动特性，且平动残余位移达到了驱动位移的0.86%，而A和C两点在y轴方向的位移方向相反，幅度相当，显示显著的转动特性，最大转动残余位移达到了驱动位移的2.7%。虽然残余平动和转动位移较大，但是由于检测梳齿为沿着y轴方向左右对称且等间距的滑膜梳齿，对平动和转动位移有一定的抑制作用。然而B点和质量块中心沿着y轴的残余位移将会直接表现为信号检测回路中的共模信号，但是该残余位移仅占驱动位移的0.021%。实际信号检测中的共模的机械耦合误差要远小于最大残余位移。

图5(a)为检测模态，两个质量块在检测方向反相运动，并且检测机构和质量块在检测方向运动显著，而驱动框架运动微弱，达到了一定的解耦效果。图5(b)为驱动框架放大图，可见解耦后驱动框架也有一定的残余运动，表现为平动与转动结合运动特性。取驱动框架中心线上的D点、E点、F点和质量块中心在x和y方向位移进行位移分析。类似，在y方向，D点、E点、F点的位移基本相等，残余位移为平动位移，且平动残余位移达到了检测位移的1.36%，而D点和F点在x轴方向的位移方向相反，残余位移表现为转动位移，最大的残余位移达到了检测位移的0.87%。类似，驱动梳齿为沿着x轴方向的滑膜梳齿，梳齿左右间隙检测相等，且所有梳齿左右对称布置，同时驱动力较大，敏感位移相比驱动位移至少小5～8个数量级， 因此残余解耦位移对驱动影响可以忽略不计。

图4 驱动模态非理想解耦特性仿真Fig.4 Non-ideal decoupled characteristics simulation of drive mode

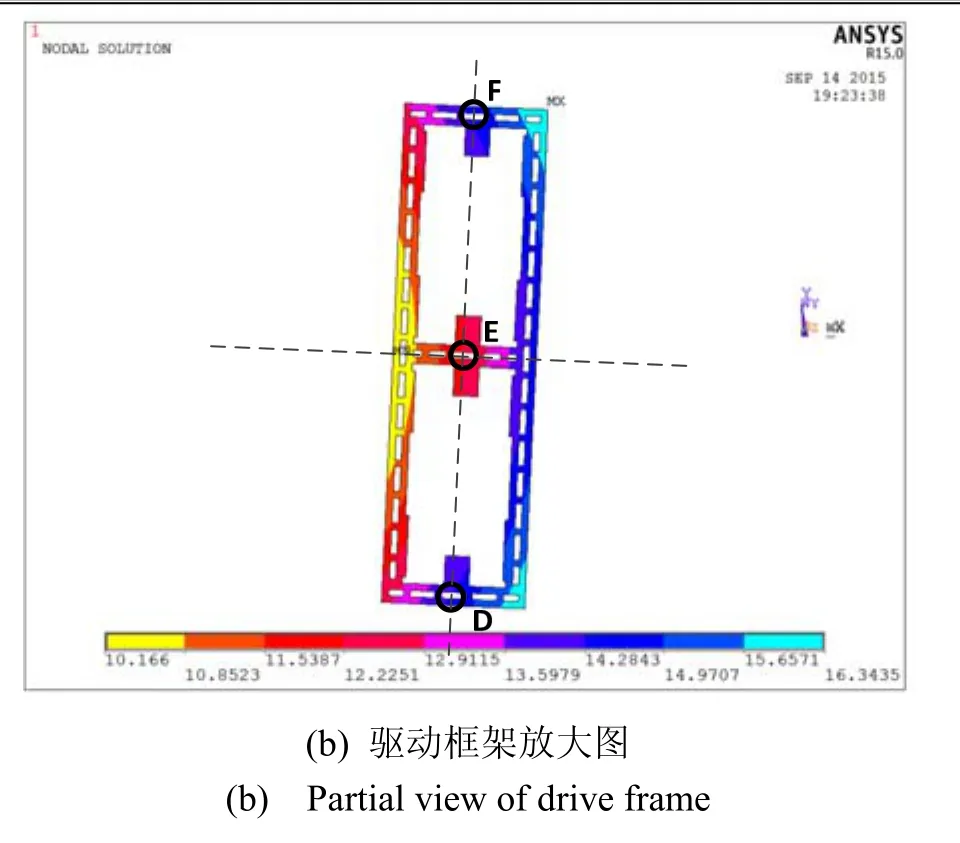
图5 检测模态非理想解耦特性仿真Fig.5 Non-ideal decoupled characteristics simulation of sense mode

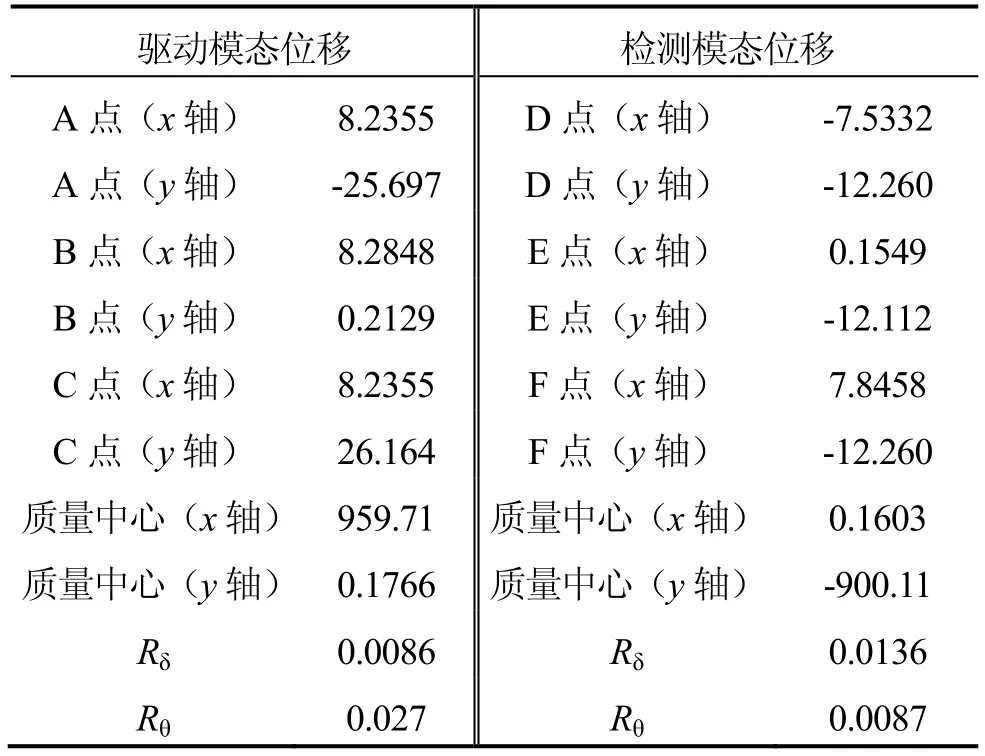
表1 非理想解耦位移Tab.1 Non-ideal decoupled displacement

4 实 验

为了对非理想的解耦特性进行试验研究，对双质量全解耦硅微陀螺仪芯片加工和测试，图6为加工的双质量全解耦硅微陀螺仪。理论上， 左右对称、等间隙的滑膜梳齿对由非理想解耦导致的平动和转动误差有一定的抑制效果，但是由于加工误差的影响，左右间隙和左右梳齿会存在一定误差，将导致部分残余平动和转动误差。另外由于加工误差，还有少部分质量块中心沿着y方向的耦合运动也会传递到敏感梳齿部分。以上三种残余误差是正交信号和失调信号的主要来源，很难分离，因此对该微陀螺结构的总误差进行了测量。图7为测试的PCB电路板，该陀螺芯片由于在驱动和检测模态都采用滑膜梳齿，在空气下品质因数超过 200，因此未采用真空封装，直接在标准大气压下进行气密封装。图 8为非理想解耦特性测试原理图，整个方案首先利用AGC (Auto Gain Control) 和精密相位控制回路实现驱动模态的同频反相驱动，然后通过接口检测电路提取解耦残余误差，再通过放大、解调来进行误差标定。

图6 加工的双质量解耦硅微陀螺仪芯片Fig.6 The processed chip of decoupled dual-mass micro-gyroscope

图7 测试PCB电路板Fig.7 The tested PCB circuits

图8 非理想解耦特性测试原理图Fig.8 Test scheme of the non-ideal decoupled characteristics

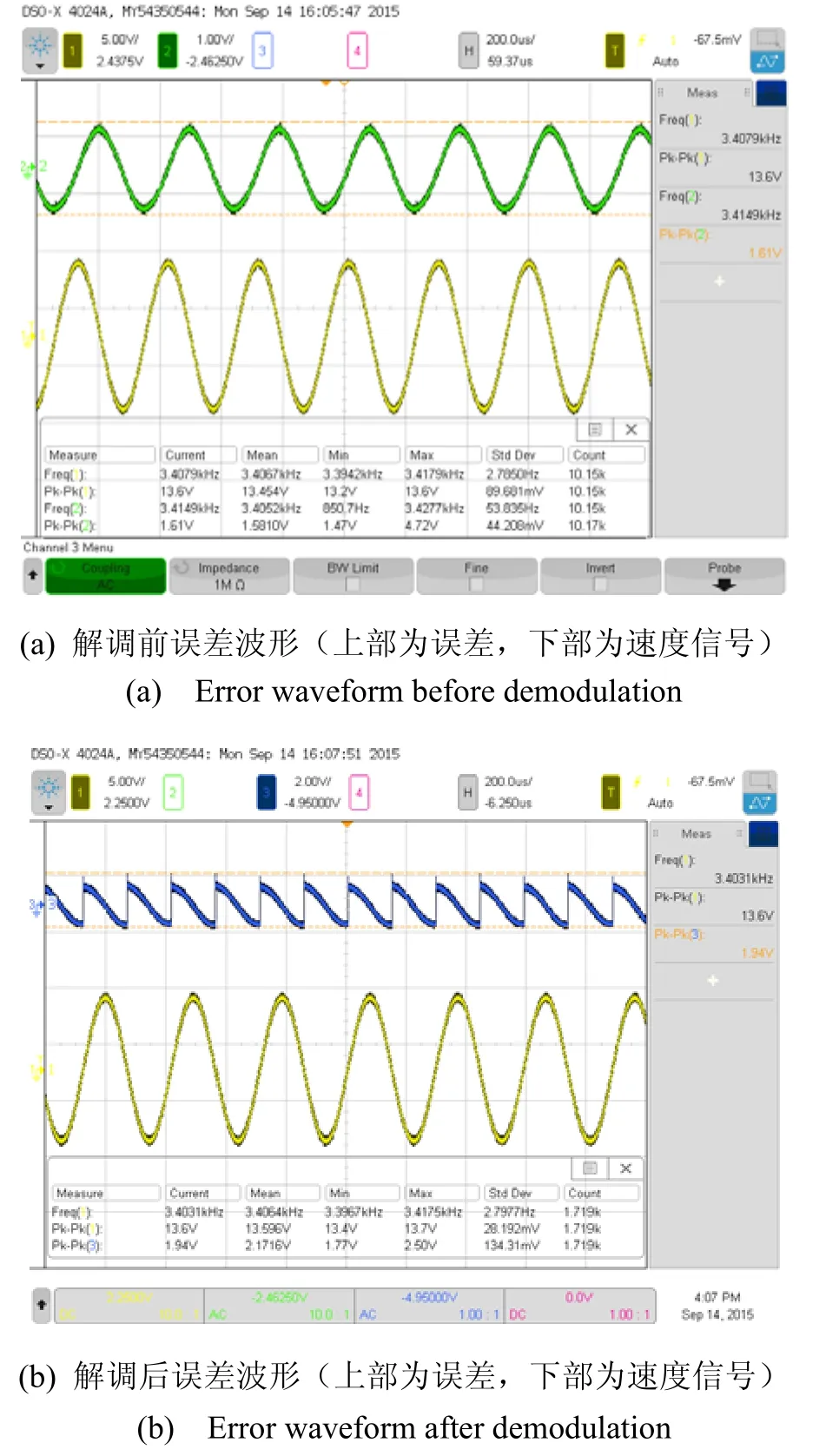
图9 误差信号波形Fig.9 Error signal waveform

图10 微陀螺输出漂移Fig.10 Output bias drift of micro-gyroscope

对非理想的解耦误差进行了测试，解调前后的误差信号波形如图9所示。由图9(b)可知，误差信号和参考的速度信号相位接近 90°，因此绝大部分的误差为正交误差。通过对标度因数进行测试，得到标度因数为19.89 mV/(°/s)，根据放大倍数，可以计算得到正交误差158.65 (°)/s，失调误差为19.03 (°)/s。同时对空气下工作的硅微陀螺仪解调后残余误差漂移特性进行了测试，如图10所示，结果表明该微陀螺偏置稳定性达到12.01 (°)/h。

5 结 论

本文首先阐述了双质量解耦硅微陀螺仪的结构原理，构建检测模态的等效模型，推导了双质量全解耦硅微陀螺仪的检测位移表达式；然后构建检测框架非理想的解耦模型，推导了检测框架非理想的平动位移与转动位移与驱动位移的比值公式；接着进行了结构非理想解耦特性仿真分析，对驱动模态时检测框架和检测模态时驱动框架的非理想解运动性进行仿真，结果表明，检测框架的残余平动位移达到驱动位移的0.86%，最大转动残余位移达到了驱动位移的2.7%，而驱动框架的平动残余位移达到了检测位移的1.36%，转动残余位移达到了检测位移的 0.87%；最后，对加工的双质量全解耦硅微陀螺结构芯片的非理想解耦误差进行了测量，结果表明空气下正交误差为158.65 (°)/s，失调误差为19.03 (°)/s，由解调后残余误差导致的偏置稳定性达到了12.01 (°)/h。

（References）：

[1] Nitzan S, Ahn C H, Su T H, Li M, et al. Epitaxiallyencapsulated polysilicon disk resonator gyroscope[C]// MEMS 2013. Taipei, Taiwan, 2013: 625-628.

[2] Eminoglu B, Kline M H, Izyumin I, et al. Background calibrated MEMS gyroscope[C]//2014 IEEE Sensors. Valencia, Spain, 2014: 922- 925.

[3] Prikhodko I P, Zotov S A, Trusov A A, et al. Foucault pendulum on a chip: Angle measuring silicon MEMS gyroscope[C]//MEMS 2011. Cancun, Mexico, 2011: 161-164.

[4] Sharma A, Zaman M F, Ayazi F. A sub-0.2o/hr bias drift micromechanical silicon gyroscope with automatic CMOS mode-matching[J]. IEEE Journal of Solid-State Circuits, 2009, 44(5): 1593-1608.

[5] Cheng P, Zhang Y J, Gu W T, et al. Effect of polarization voltage on the measured quality factor of a multiple-beam tuning-fork gyroscope[J]. Sensors and Actuators A, 2012, 187: 118-126.

[6] Sonmezoglu S, Gavcar H D, Azgin K, et al. Simultaneous Detection of Linear and Coriolis Accelerations on A Mode-matched MEMS Gyroscope[C]//MEMS 2014. San Francisco, CA, USA, 2014: 32-35.

[7] Alper S E, Akin T. Symmetrical and decoupled nickel microgyroscope on insulating substrate[J]. Sensors and Actuators A, 2004,115:336-350 .

[8] Trusov A A, Schofield A R, Shkel A M. Micromachined rate gyroscope architecture with ultra-high quality factor and improved mode ordering[J]. Sensors and Actuators A, 2011, 165: 26-34.

[9] Bo Dai, Bo Yang, Hui Zhao, et al. Structural design and simulation of a fully decoupled dual-mass micro-gyroscope [J]. Applied Mechanics and Materials, 2014, 529: 334-338.

[10] Yang Bo, Wang Shou-rong, Li Hong-sheng. Structure error analysis and system performance test of decoupled silicon micro-gyroscope[J]. Nanotechnology and Precision Engineering, 2010, 8(6): 1628-1631.

Non-ideal decoupled characteristics’ research and system performance test of dual-mass decoupled silicon micro-gyroscope

YANG Bo1,2, WU Lei1,2, ZHOU Hao3, HU Di1,2, LIU Xian-xue3
(1. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 2. Key laboratory of Micro-Inertial Instrument and Advanced Navigation Technology, Ministry of Education, Nanjing 210096, China; 3. Institute of Electronic Engineering, China Academy of Engineering Physics, Mianyang 621999, China)

The non-ideal decoupled characteristics of the micro-gyroscope structure were studied to analyze the mechanical coupling error of dual-mass decoupled micro-gyroscope. At first, the working principle of dual-mass decoupled micro-gyroscope was described, and the sense displacement of dual-mass decoupled micro-gyroscope was deduced. Then the non-ideal decoupled model of sense frame was constructed in the drive mode. The equations of the parallel displacement and rotational displacement due to the non-ideal decoupling were derived. Simulation analysis on the non-ideal decoupling in structure was implemented. The non-ideal motion characteristics of sense frame in drive mode and the drive frame in the sense mode were simulated. Simulation results show that, the residual parallel displacement of sense frame is up to 0.86% of drive displacement and the residual maximum rotation displacement of sense frame is 2.7% of drive displacement in the drive mode, while the residual parallel displacement of drive frame is 1.36% of the sense displacement and the residual maximum rotation displacement of drive frame is 0.87% of sense displacement in the sense mode. Finally, the non-ideal decoupling error of the processed structure chip of dual-mass decoupled micro-gyroscope was measured, and the results show that the quadrature error without vacuum encapsulation is 158.65 (º)/s, the offset error is 19.03 (º)/s, and the bias stability is 12.01 (º)/h.

silicon micro-gyroscope; dual-mass; non-ideal decoupled; non-vacuum encapsulation

U666.1

：A

2015-09-18；

：2015-11-29

国家自然科学基金委员会和中国工程物理研究院联合基金资助（U1230114）；国家自然科学基金资助（61571126，61104217）；航空科学基金（20150869005）

杨波（1979—），男，副教授，博士生导师，从事微惯性仪表与MEMS传感器研究。Email: yangbo20022002@163.com

1005-6734(2015)06-0794-06

10.13695/j.cnki.12-1222/o3.2015.06.017