升力式火星探测器进入轨迹优化设计仿真
2015-06-15刘涛南英胡海龙
刘涛 南英 胡海龙
(1 南京航空航天大学航天学院,南京210016) (2 上海航天八院八部,上海200000)
升力式火星探测器进入轨迹优化设计仿真
刘涛1南英1胡海龙2
(1 南京航空航天大学航天学院,南京210016) (2 上海航天八院八部,上海200000)
针对升力式火星探测器在其完成星际转移轨道之后,由预定进入点开始反冲制动改变运行轨道进入火星大气,设计并仿真了进入段的轨迹优化。根据火星的大气密度及引力场参数,建立相应的火星大气模型及引力场模型,确定了升力式火星探测器的运动方程。在满足进入过程的约束条件下,采用遗传算法对进入轨道进行优化设计,提出不同的推力发动机制动方案并进行分析比较。结果表明,采用推力方案二能够实现性能指标最优,并求得着陆速度为13.6m/s,最终实现了探测器在火星表面的软着陆。
轨迹优化; 大气模型; 引力场模型; 遗传算法;火星探测器
1 引言
由于在太阳系中的特殊位置,火星是太阳系中与地球生态环境最相似的一颗行星,所以火星探测一直是世界各国深空探测工程中的热门话题。以“凤凰号”和“火星科学实验室”为代表的新一代的火星探测器,通过控制升力从而控制飞行轨迹,并使用降落伞配以反冲变推力发动机制动在火星表面成功软着陆。中国也初步提出了未来15~20年以月球和火星为主的深空探测工程研究计划。随着深空探测技术的迅猛发展,在未来可预见的时间内,人类可实现航天飞机形式的有翼式升力星际探测器[1-4],通过火星大气及火箭发动机反冲制动配合升力式进入火星,从而实现更大运载的探测器在目标星球的软着陆。
火星进入轨迹优化设计是火星探测的关键技术之一,与航天器再入返回地球类似,由于火星上存在大气层,因此要实现火星探测器在火星表面的软着陆[1-5],就可以充分利用其大气对探测器实现气动减速,使其在火星表面安全着陆。软着陆就是探测器下降过程中采用降落伞或者反推火箭降低下降速度,到达火星表面时仍保持探测器正常工作状态的着陆方式。参照航天飞机返回地球,将火星表面软着陆指标定为:轨道高度为3.5 km,速度为(150±6)m/s。探测器采用航天飞机型升力式气动布局(美国和日本均已有相应的火星飞机设计方案),具有较好的升力特性,可充分利用火星大气层的减速作用配合反冲推力发动机制动,实现探测器在火星表面的软着陆。
建立火星的大气密度模型及引力场模型[5-8],由进入点开始采用制动推力发动机进行反冲,根据不同进入阶段的推力发动机反冲制动方案,在满足过载、动压等约束条件下,通过遗传算法全局寻优优化性能指标[9-10],分析不同发动机制动方案下的轨迹特性及燃料消耗情况,选取最优性能的发动机反冲制动方案及进入轨迹。
2 火星探测器运动模型
火星探测器的运动方程为
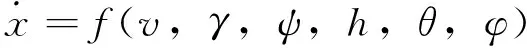
式中v为探测器飞行速度;γ为轨迹倾角;ψ为偏航角;h为探测器飞行高度;θ为探测器所在位置经度;φ为探测器所在位置纬度。
对升力式火星探测器进入过程作如下假设:探测器看作运动的质点,飞控系统处于理想工作状态;大气相对火星静止,且同一高度分布均匀;只考虑火星自转,忽略其公转。其进入飞行轨迹运动方程为
(1)
式中α、β分别为探测器攻角及侧滑角;σ为滚转角;P为火箭推力;m为探测器质量;mc为反冲发动机每秒消耗燃料质量;CL,CD分别为升力、阻力系数;ρ为火星大气密度;ωe为火星自转角速度;rm为火星半径;r为火星质心与航天器质心的距离;S为探测器参考面积;x、z分别为经度坐标、纬度坐标,单位km;g为火星表面重力加速度;G为火星不同高度处重力加速度;q为动压。
3 相关设计参数
(1)火星探测器气动参数
升阻比模型采用航天飞机轨道飞行器的气动参数模型,具体参数设置如下:
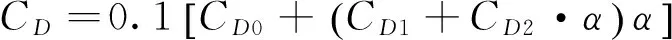
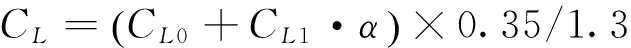
根据工程环境实际,取CD0=0.078 5,CD1=-0.006 2,CD2=0.621 4×10-3,CL0=-0.207 04,CL1=0.029 244。
(2)反冲推力发动机
反冲推力发动机3台;推进剂为液氧、液氢;推力为真空4kN;比冲为4 000N·s/kg;探测器结构质量为2 000kg;推进剂质量为2 000kg。
(3)火星大气密度
在大气进入段一般认为着陆器受推力的作用,只利用空气动力进行机动,在这个过程中着陆器受到的外力只有重力和空气动力。地球与火星大气环境参数见表1。
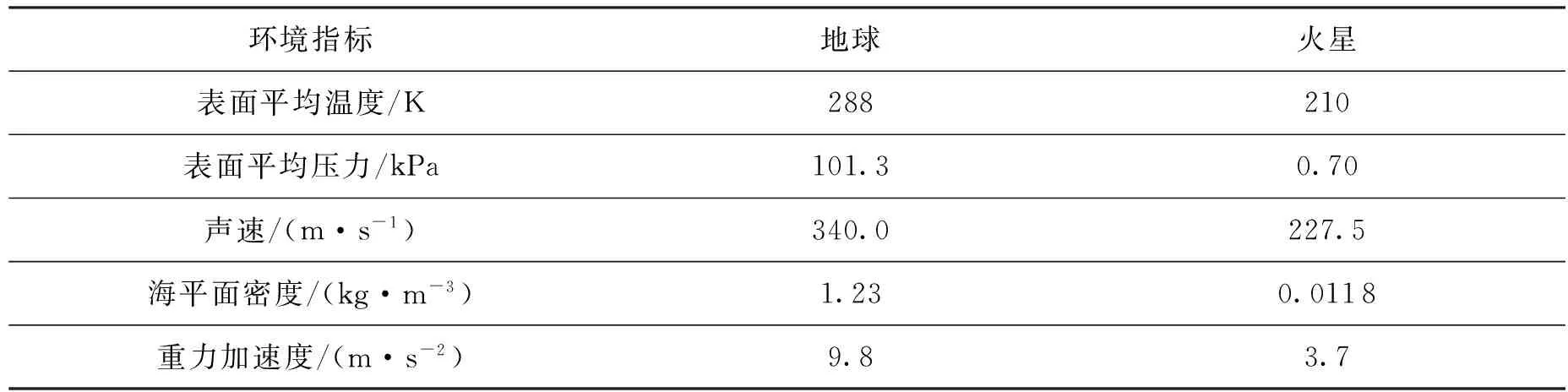
表1 地球与火星大气环境参数比较
本文采用指数大气密度模型
(2)
式中r0为径向基准位置,r0=3 437.2 km(距离火星表面40km);ρ0为火星海平面的大气密度,ρ0=0.011 8;hs为大气定标高度,hs=7 000 m。值得指出,火星表面的火星大气密度,相当于在离地球表面34 km高度处的地球大气密度。
(4)火星引力场
火星的引力场并不均匀,精确的引力模型可以用一系列球谐函数的和来表示。本文采用简化的重力场模型
(3)
式中μ为火星的引力常数,μ=4.282 849×1013m3/s2。
(5)气动加热率
火星探测器进入大气层,由于对前方空气的压缩及周围空气的摩擦,有部分动能转变成空气的热能使探测器受热。对于探测器不同部位,其气动加热的严重程度是不同的,在此只考虑相对严重的临界加热区的气动加热效应,以鼻锥驻点区的气动加热作为设计基准。其半经验公式为
(4)
式中RS为鼻锥驻点区曲率半径;CS为常量;vc为环绕速度,vc=7 800m/s。
4 推力发动机工作方案
本文对发动机的推力控制方案进行简化处理,根据飞行高度对发动机进行推力控制。
考虑到火星大气稠密程度对探测器的气动减速会产生很大影响。因此可将火星大气分为无大气、大气密度小、大气密度较大三个阶段。由于火星表面大气密度、温度及压强与高度的函数关系具有单调性,故分析火星探测器的飞行状态,可简化为三段不同高度段火星探测器的飞行状态。
本文采用静压高度控制法,实现不同高度段推力发动机的开关动作。静压高度控制法,是指利用大气静压和高度的对应关系控制发动机的工作状态,根据基于飞机上常用的气压式高度表的工作原理, 即通过气压式高度表感应当地的大气静压力,间接推算出当地的高度,从而在某一指定高度发出发动机工作指令。
火星大气压强与高度的近似数值关系为
(5)
由于进入过程中探测器发动机数量过多会导致燃料消耗量的增加,有效载荷的质量减小,而发动机数量过少,发动机推力方案的设置会更少,不具备最优化选择的条件。当三台反推发动机同时工作时最大可提供12kN的反推力,可以起到足够的反推制动的作用,因此为研究方便,本文选取三台发动机。推力发动机工作方案设置为:将火星探测器的飞行高度均匀分为三段h1、h2、h3,控制三个主推力发动机(三个推力发动机分别为F1、F2、F3)的开关状态来实现不同飞行高度阶段的推力控制。
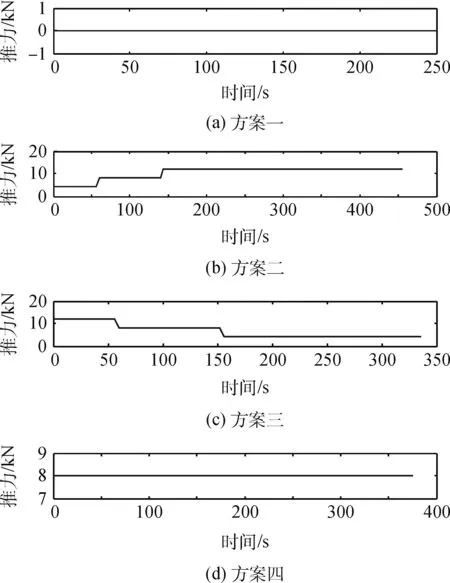
方案一:火星探测器所有推力发动机进入过程中F1、F2、F3均不工作,即无动力进入火星大气层。
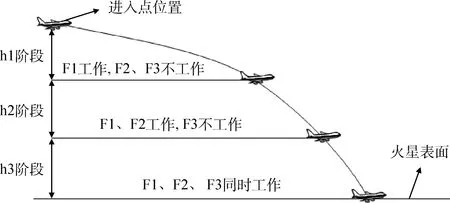
图1 方案二推力发动机工作示意
方案二:火星探测器在进入过程中,h1阶段,F1工作;h2阶段,打开发动机F2,F1、F2工作;h3阶段,打开发动机F3,F1、F2、F3均工作。过程示意图见图1。
方案三:火星探测器在进入过程中,h1阶段,F1、F2、F3均工作;h2阶段,关闭发动机F3,F1、F2工作;h3阶段,关闭发动机F2,F1工作。
方案四:火星探测器在进入过程中,两个推力发动机F1,F2全程工作,F3不工作。
5 火星探测器进入飞行轨迹优化算法
探测器进入轨迹优化可以看作一个多目标优化问题,采用权重系数变换法进行优化求解,即在满足加热率、过载和动压等给定的约束条件下,寻找最优控制律u(t)*,u=[α,σ],α为攻角,σ为滚转角,使得再入过程中总加热量、总过载和总动压最小。等效的优化问题可以描述为
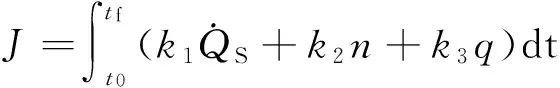
(6)

1)染色体编码。采用直接离散的参数化方法将控制变量u(t)离散,设t∈T,取步长Δt,时间域离散为0=t 2)适应度函数设计。采用罚函数处理不等式约束,将约束写入目标函数 (7) 式中σshare为小生境半径;dij为解空间上的度量。 3)确定遗传算子。选择算子采用最优保存策略的选择方式,交叉算子选用单点交叉方式,变异算子采取基本位变异方式。 4)初始化状态参数。设置遗传算法的基本运行参数,优化得到最优性能再入轨迹。 火星探测器进入过程中,计算参数及其相应约束设置如下: S=50m2;M=2 000kg;m=2 000kg; 遗传算法的运行参数为: 种群100, 染色体长度30,选择概率0.93,变异概率0.15,运行代数为800代,小生境半径1.6。 初始状态参数设置为:v=3 435 m/s,γ=-3.74°,ψ=10°,h=120 km,θ=0.174 5 rad,φ=0.226 9 rad。 对于四种不同的发动机方案的仿真结果如图2~图5所示。 图2 各推力方案推力随时间变化曲线 在对比推力方案的同时,调整火星探测器升阻比,计算其无升力进入的轨迹特性,得到以下数据结果如表2~表3所示。 仿真结果分析如下: 1)升力式与无升力进入比较——无升力进入方式着陆速度大,所受气动力小,进入过程过载小;其气动加热率与升力式进入相比,是其8倍左右,是工程上所不能接受的。 2)有推力制动与无推力制动进入方案比较——方案一与其他有推力方案相比,火星探测器着陆速度大,无推力进入过程中最大气动加热率、过载均比较大,也不能实现火星探测器的软着陆。 3)有推力制动进入方案比较——有推力反冲制动方案中方案二着陆速度最小,燃料消耗最多,火星探测器飞行时间最长,过载和气动加热率也较小,满足软着陆要求;方案三的燃料消耗最少,着陆速度较大,不满足软着陆要求;方案四在三者中最大过载及气动加热率均最小,但是着陆速度较大,不满足软着陆要求。 图3 各推力方案速度与高度随时间变化曲线 图4 各推力方案过载与气动加热率随时间变化曲线 图5 各推力方案的3-D飞行轨迹图 火星探测器进入过程中,从120km高度进入,均匀三等分为80~120km,40~80km,0~40km三个阶段。由于火星大气高度约为70km,故第一高度段无火星大气,只有推力发动机反冲制动减速;第二高度段有火星大气,但火星大气密度小,所受到的气动力较小,主要还是反冲推力发动机制动;第三高度段火星大气密度较大,受明显气动力作用,此时受气动力和推力发动机同时作用,减速效果明显。故理论上,在第一高度段及第二高度段,推力反冲减速不能过大,应保留适当的飞行速度进入火星大气稠密段。由于火星探测器所受气动力与飞行速度平方呈正比关系,故此时气动力减速效果显著,充分利用火星大气的气动减速作用,实现在火星表面的软着陆。推力方案二的仿真结果表明这种推力方法是可行的,且效果很好。 表2 升力式与无升力进入结果对比 表3 各推力方案仿真结果对比 [1]NUMATA D. Characteristics of thermal anemometers at low-pressure condition in a Mars wind tunnel[R].AIAA 2011-1166. [2]KINNEY D J. Aerodynamic and aero thermal environment models for a Mars entry, descent, and landing systems analysis study[R]. AIAA 2011-1189. [3]TSUJI K, SUNADA S. Flutter of an aircraft flying on Mars[J].Journal of Aircraft,2011, 48(1):341-343. [4]KUHL C A. Trade study of multiple thruster options for the Mars airplane concept[R]. NASA/TM-2009-215699. [5]翟盘茂, 郭艳君. 高空大气温度变化研究[J].气候变化研究进展, 2006(9): 42-43. QU PANMAO, GUO YANJUN. A study of upper air temperature change [J]. Advances in Climate Change Research, 2006(9):42-43. [6]高滨. 火星探测器着陆技术[J] 航天返回与遥感, 2009,30(1):1-9. GAO BIN. Mars exploration entry, descent and landing technologies [J]. Spacecraft Recovery & Remote Sensing, 2009, 30(1):1-9. [7]贾贺,荣伟. 火星探测器减速着陆技术分析[J]. 航天返回与遥感,2010,31(3):6-14. JIA HE, RONG WEI. Mars exploration deceleration landing technology analysis [J]. Spacecraft Recovery & Remote Sensing,2010,31(3):6-14. [8]荣伟.火星探测器减速着陆技术研究[D].北京: 中国空间技术研究院, 2008. RONG WEI. Mars exploration deceleration landing technology research [D]. Beijing: China Academy of Space Technology,2008. [9]陈刚,万志明.基于遗传算法的RLV再入轨迹优化设计[J].系统工程与电子技术,2006,28(8):1240-1243. CHEN GANG, WAN ZIMING. Genetic algorithm optimization of RLV reentry trajectory [J]. Systems Engineering and Electronics, 2006,28(8):1240-1243. [10]陈刚,万志明.遗传算法在航天器轨迹优化中的应用 [J].弹道学报,2006,18(1):1-5. CHEN GANG, WAN ZIMING. Overview of spacecraft trajectory optimization using genetic algorithm [J]. Journal of Ballistics,2006,18(1):1-5. [11]PRAKASH R, BURKHART P D, CHEN A, et al. Mars science laboratory entry, descent, and landing system overview[C]∥IEEE Aerospace Conference,2008. [12]SCHOENENBERGER M, DYAKONOV A, BUNING P. Aerodynamic challenges for the Mars science laboratory entry descent and landing[C]∥41st AIAA Thermophysics Conference, San Antonio, Texas, June 22-25, 2009. [13]MITCHELTREE R, STELTZNER A, CHEN A, et al. Mars science laboratory entry descent and landing system verification and validation program[C]∥IEEE Aerospace Conference, 2008. [14]WAY D W, POWELL R W, CHEN A, et al. Mars science laboratory: entry, descent, and landing system performance[C]∥IEEE Aerospace Conference, Big Sky, MT, 2006:1467-1501. [15]BIRGE B K. A computational intelligence approach to the Mars precision landing problem [D]. Raleigh: North Carolina State University,2008. (编辑:高珍) Optimal Entry Trajectory Design of Winged Mars Probe LIU Tao1NAN Ying1HU Hailong2 (1 School of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016)(2 The 8th Institute of Shanghai Academy of Space Flight Technology, Shanghai 210000) This paper provides an optimal entry trajectory of the winged Mars probe, right after it changed the orbit into the Martian atmosphere braked by reverse thrust engine. This paper establishes Martian atmosphere model and gravitational field model corresponding on the density of the Martian atmosphere and gravitational field parameters, and determined the dynamic equations of the Mars probe. Within all the constraint conditions in the entering process, this paper designs an optimal entry trajectory based on the genetic algorithm. In addition,this paper provides different thrust engine scheme through comparing them. The results show that the second scheme can achieve the optimal performance index and the landing speed is 13.6 m/s,ultimately realizing the minimum consumption of energy and aerodynamic heat emission structure quality in the process of entering and soft landing. Trajectory optimization; Atmospheric model; Gravitational field model; Genetic algorithm;Mars probe 2015-03-20。收修改稿日期:2015-08-20 10.3780/j.issn.1000-758X.2015.06.010 刘 涛 1990年生,现为南京航空航天大学控制工程专业硕士研究生。研究方向为航天器轨迹优化与控制。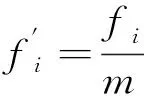
6 仿真及结果分析