基于卫星在轨温度预示热控涂层性能退化的方法

宋馨 张有为 刘自军 斯东波

(北京空间飞行器总体设计部，北京 100094)

基于卫星在轨温度预示热控涂层性能退化的方法

宋馨 张有为 刘自军 斯东波

(北京空间飞行器总体设计部，北京 100094)

介绍了一种利用卫星在轨温度数据预示热控涂层在轨性能退化情况的方法，建立并推导了适用于研究热控涂层随整数年变化规律的数学模型，该模型利用卫星设备的温度曲线通过反演计算得到设备表面热控涂层的退化数据。为检验本文数学模型的计算效果，构造了一组数值试验，结果表明本文数学模型的计算数据与真实值非常接近，说明本文建立的数学模型能够很好地根据卫星在轨温度计算出热控涂层在轨退化数据。

热控涂层；性能退化；数值模拟；在轨数据反演；卫星

1 引言

热控涂层在卫星热控制领域得到了非常广泛的应用，热控涂层的两个重要热辐射性能参数太阳吸收比和发射率决定了暴露于空间环境中卫星表面的温度水平。由于卫星在轨运行期间会受到原子氧、紫外线、带电粒子等空间辐射的作用使热控涂层的性能发生退化，主要表现为太阳吸收比增大[1]，导致卫星温度升高，影响卫星的正常运行和在轨安全。因此，研究卫星热控涂层性能的退化规律，对于卫星在轨安全运行和卫星热控设计都非常重要。NASA通过在轨飞行试验和地面模拟试验研究了热控涂层性能退化规律[2-3]；我国在“东方红二号”卫星上对热控涂层(OSR)的在轨性能退化情况进行了测试[4]；文献[5-7]中研制了一套空间辐射环境模拟试验系统，对常用热控涂层的性能退化进行了大量试验研究；文献[8]对热控涂层性能退化的机理进行了理论研究。

由于在卫星上搭载热控涂层监视装置所消耗的资源代价非常大，目前的热控涂层性能退化研究工作仍然以地面试验和理论分析为主。热控涂层性能的退化会直接反映到卫星温度水平的变化上，而我国发射的各类卫星在轨飞行过程中又积累了大量温度数据，因此可选取不同时间卫星在轨温度数据并通过计算比较得到热控涂层性能退化规律。本文从一维传热问题出发，探讨了基于卫星在轨温度数据通过反演计算研究热控涂层在轨性能退化情况的方法，并通过模拟算例对计算效果进行了验证。

2 数学模型

2.1 一维传热方程

本文研究的为一维传热问题，研究对象为安装在某人造地球卫星上的一台设备，设备的特征尺寸为L，在x=0处为绝热边界，在x=L处与宇宙空间辐射换热，一维瞬态传热方程为

(1)

(2)

(3)

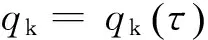
(4)

式中αk为研究对象与宇宙空间换热表面的太阳吸收比；Es、Ee、Er分别为太阳辐射强度、地球红外辐射强度以及地球反照的太阳辐射强度。

2.2 热控涂层性能退化计算公式推导

为研究热控涂层在轨性能退化，总体思路是从某时刻τ1开始，截取τ1～τ1+Δτ时段的研究对象在轨温度变化曲线，反演得到这段时间内研究对象的吸收外热流qk，然后由式(4)计算得到αk，下面对式(4)中各项进行逐个分析：

1)qk为研究对象与宇宙空间换热表面的吸收外热流值，在已知研究对象在轨温度变化曲线的情况下，采用导热反问题方法由研究对象的温度曲线反演得到，为已知量，导热反问题反演过程将在第2.3节中给出。

2)Es为太阳辐射强度，对于给定的轨道及轨道位置，太阳辐射强度的量值有成熟的公式可以计算得到，太阳辐射与研究对象受照表面的角度关系也能由卫星轨道与太阳辐射的位置关系计算得到，为已知量。

3)Ee为地球红外辐射强度，与大气温度、地表温度、地形地貌等很多因素有关，地球红外辐射的测量及计算非常困难，为未知量。

4)Er为地球反照的太阳辐射强度，与地表热辐射特性、海洋湖泊分布、大气传输和散射特性等很多因素有关，地球反照的太阳辐射强度的测量及计算非常困难，为未知量。

5)εk为研究对象与宇宙空间换热表面的发射率，已有热控涂层性能退化研究工作表明，热控涂层在轨性能退化主要表现为太阳吸收比的变化，εk退化很小可视为不变[1]，因此εk可以在卫星发射前通过地面试验测量得到，为已知量。

通过分析看到，式(4)中除了αk这个未知量外，还有地球红外辐射强度Ee和地球反照的太阳辐射强度Er为未知量，下面通过引入一些新条件逐个消去这些未知量。为消去未知量Ee，引入一台参照设备，设备的安装位置和角度应满足两个条件：

条件1：参照设备与宇宙空间辐射换热表面的到达外热流条件需要与研究对象的相同，根据卫星上设备的安装位置和布局筛选出符合条件的设备。

条件2：参照设备与宇宙空间辐射换热表面的热控涂层性能参数为已知量，这需要找到热控涂层性能在轨退化很少、基本不变的涂层(如铝合金黑色阳极氧化[1])，则在卫星发射前通过地面试验测量得到太阳吸收比和发射率的值；或者在轨退化规律已经研究清楚、有确定数据的热控涂层，这样在卫星在轨飞行期间参照设备的太阳吸收比和发射率为已知量。

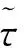
(5)

(6)

(7)

消去地球红外辐射强度Ee后，式(7)中还需要消去地球反照的太阳辐射强度Er。为此，选取另外一个时间段τ2～τ2+Δτ在轨温度变化曲线。选取τ2～τ2+Δτ时段应满足两个条件：

条件3：τ2～τ2+Δτ时段与τ1～τ1+Δτ时段在卫星飞行轨道上的位置相同。

条件4：τ2～τ2+Δτ时段与τ1～τ1+Δτ时段的太阳对地球的辐照条件相同，这种情况往往出现在τ2～τ2+Δτ时段与τ1～τ1+Δτ时段的时间间隔相差为整数年的情况，因此这个条件也使本文提出的数学模型适合于研究热控涂层性能随整数年的退化规律。

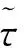
(8)

(9)

(10)

根据选取τ2～τ2+Δτ时段的限制条件4，τ2～τ2+Δτ时段与τ1～τ1+Δτ时段的太阳对地球的辐照条件相同，可得：

(11)

另外由于影响地球反照太阳辐射强度的地表热辐射特性、海洋湖泊分布、大气传输和散射特性等因素在几年或几十年周期内可视为状态变化不大、比较稳定，因此可近似认为

(12)

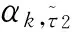
(13)

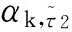
2.3 导热反问题

导热反问题是利用研究对象的测量温度，通过一定反演算法计算得到热物性参数、边界条件等未知量的一类问题。对于本文研究的一维瞬态传热问题，传热方程为

(14)

(15)

(16)

初始条件为

(17)

从式(16)中可以看到，由于边界条件中引入了表征辐射热流的4次方非线性项，大大增加了导热反问题的不适定性，因此采用抗不适定性能力较强的共轭梯度法进行求解。

共轭梯度法的目标函数为

(18)

式中Tcal,n为设备温度计算值；Tmea,n为设备温度在轨遥测值；n为不同时间点。吸收外热流值q的迭代式为

(19)

式中b为迭代次数，d为搜索方向，其计算式为

(20)

γ由式(21)计算

(21)

迭代步长β为

(22)

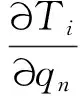
(23)

边界条件式(15)、式(16)对qn求微分得到：

(24)

(25)

式(25)中

(26)

灵敏度方程的初始条件由式(17)对qn求微分得到：

(27)

(28)

共轭梯度法的收敛目标是使式(29)成立：

(29)

式中δ为很小的正数。共轭梯度法的求解步骤如下：

1)求解传热方程式(14)得到温度计算值Tcal,n。

3)根据温度计算值和在轨遥测值，检查收敛目标式(29)是否达到；如果达到收敛目标，则停止迭代，否则,转入第4)步。

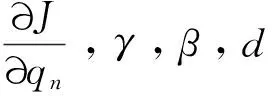
2.4 计算热控涂层在轨性能退化的计算过程

计算热控涂层在轨性能退化的步骤为：

3)求解导热反问题，反演出研究对象和参照设备的温度曲线在τ1～τ1+Δτ和τ2～τ2+Δτ时段的吸收外热流曲线qk,τ1～τ1+Δτ、qc,τ1～τ1+Δτ、qk,τ2～τ2+Δτ、qc,τ2～τ2+Δτ。

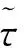
3 数值验证

下面构造一组数值算例对数学模型的效果进行检验。首先假设一组热控涂层在轨退化情况的虚拟算例，计算得到热控涂层退化前以及退化后卫星设备的在轨温度曲线，虚拟算例中的计算结果视为真实值；然后根据虚拟算例中的部分数据，通过前面推导的数学模型进行反演计算，计算结果与虚拟算例中的真实值比较，检验数学模型的效果。

3.1 虚拟算例

选取卫星上某设备做为研究对象，其传热过程可视为一维传热，特征尺寸方向L=5 mm，材料为铝合金，设备内表面为绝热边界条件；外表面与宇宙空间环境通过辐射交换热量，表面状态为喷涂SR107热控白漆。

选取某设备做为参照设备，其传热过程为一维传热，特征尺寸方向L=8 mm，材料为铝合金，设备内表面为绝热边界条件，外表面与宇宙空间环境通过辐射交换热量，表面状态为铝合金黑色阳极氧化。研究对象和参照设备的安装位置和布局使研究对象外表面与参照设备外表面到达外热流情况相同，符合条件1和条件2。

热物理参数取值为铝合金密度ρ=2 700 kg/m3、比热容cp=900 J/(kg·K)、导热系数k=120 W/(m·K)。热辐射性能参数取值为：SR107热控白漆的地面测量值αk,τ0=0.18、εk=0.85，刚入轨后一段时间SR107热控白漆热辐射性能无退化即αk,τ1～τ1+Δτ=0.18，5年后退化为αk,τ2～τ2+Δτ=0.3；铝合金黑色阳极氧化的地面测量值αc,τ0=0.87、εc=0.87，在轨飞行过程中铝合金黑色阳极氧化热辐射性能无退化，即αc,τ1～τ1+Δτ=αc,τ2～τ2+Δτ=0.87。

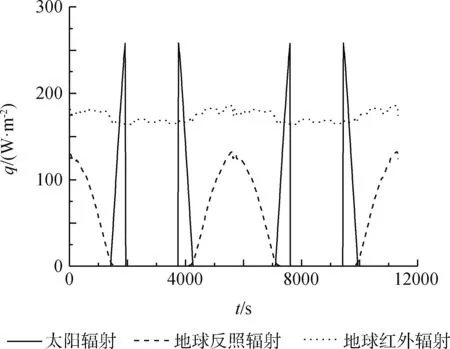
图1 到达外热流曲线

选取发射入轨后不久的12 000s时间段做为τ1～τ1+Δτ段，并根据条件3和条件4选择发射5年后的12 000s时间段做为τ2～τ2+Δτ时段，研究对象和参照设备外表面到达的太阳辐射、地球红外辐射、地球反射太阳辐射如图1所示。

根据研究对象和参照设备外表面无退化和5年退化后的表面热控涂层的热辐射参数可由图1中各项到达外热流值计算出τ1～τ1+Δτ时段以及τ2～τ2+Δτ时段外表面的吸收外热值，图2和图3分别给出了研究对象无退化和5年退化后的吸收外热流曲线。

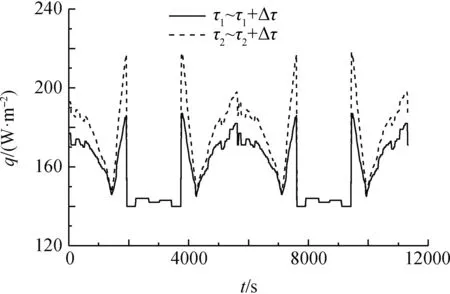
图2 研究对象吸收外热流

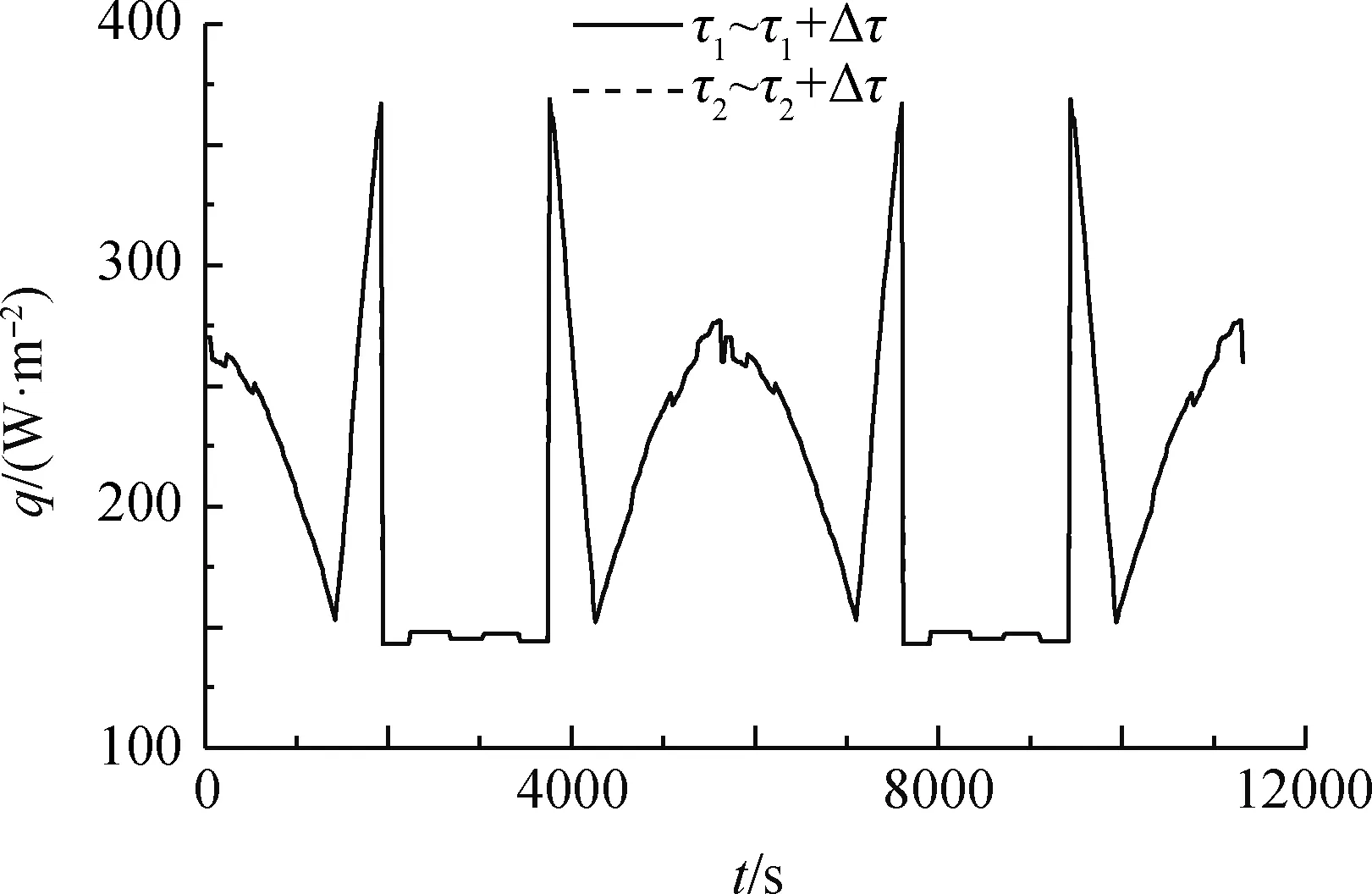
图3 参照设备吸收外热流

图4 单元划分示意

研究对象和参照设备沿特征尺寸方向划分为5个单元，测温点粘贴在第3个单元上，如图4所示。

求解式(1)～式(3)组成的一维瞬态传热方程即可计算得到研究对象和参照设备分别在τ1～τ1+Δτ时段以及τ2～τ2+Δτ时段的在轨温度曲线，如图5和图6所示。

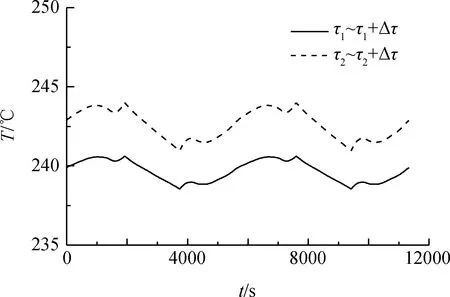
图5 研究对象在轨温度曲线

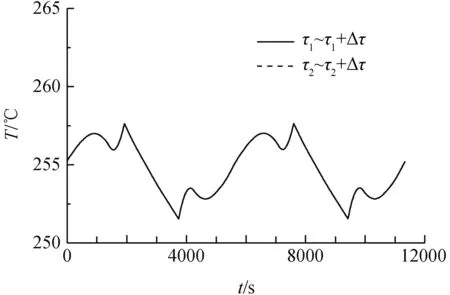
图6 参照设备在轨温度曲线

3.2 数学模型的检验

通过本文建立的数学模型，根据卫星设备在轨温度计算热控涂层在轨性能退化情况。进行计算时能够获得的全部数据为

1)已知条件1：研究对象，传热过程可视为一维传热，特征尺寸方向L=5mm，材料为铝合金，内表面为绝热边界条件，外表面喷涂SR107热控白漆。

2)已知条件2：参照设备，传热过程可视为一维传热，特征尺寸方向L=8mm，材料为铝合金，内表面为绝热边界条件，外表面为铝合金黑色阳极氧化。

3)已知条件3：地面通过试验测量得到铝合金密度ρ=2 700kg/m3、比热容cp=900J/(kg·K)、导热系数k=120W/(m·K)。

4)已知条件4：SR107热控白漆的地面测量值αk,τ0=0.18、εk=0.85；铝合金黑色阳极氧化的地面测量值αc,τ0=0.87、εc=0.87，在轨飞行过程中铝合金黑色阳极氧化热辐射性能无退化。

5)已知条件5：研究对象和参照设备在轨温度曲线，由卫星飞行过程中通过地面遥测得到。

按照2.4节计算热控涂层在轨性能退化的步骤进行计算分析：

1)根据已知条件1～已知条件4，可以得到步骤1)所需的各项数据。

2)根据已知条件5，从卫星飞行遥测数据中找出在τ1～τ1+Δτ时段以及τ2～τ2+Δτ时段的在轨温度曲线，即图5和图6。

3)根据图5和图6，进行4次导热反问题反演求解，设备初始温度取图5和图6中0时刻的值，计算出所要研究的设备和参照设备的温度曲线在τ1～τ1+Δτ时段以及τ2～τ2+Δτ时段的吸收外热流曲线；从图2和图3可以看到，研究对象以及参照设备在无退化和5年退化后的吸收外热流曲线波动变化都非常剧烈，并且辐射边界条件中引入的4次非线性项更加增大了导热反问题反演的难度；导热反问题反演得到的qk,τ1～τ1+Δτ、qc,τ1～τ1+Δτ、qk,τ2～τ3+Δτ、qc,τ2～τ2+Δτ曲线与真实值(图2和图3)比较如图7～图10所示，从图中可以看到，导热反问题较好地反演出了吸收外热流真实值，最大相对偏差为3.9%。

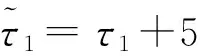
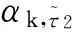
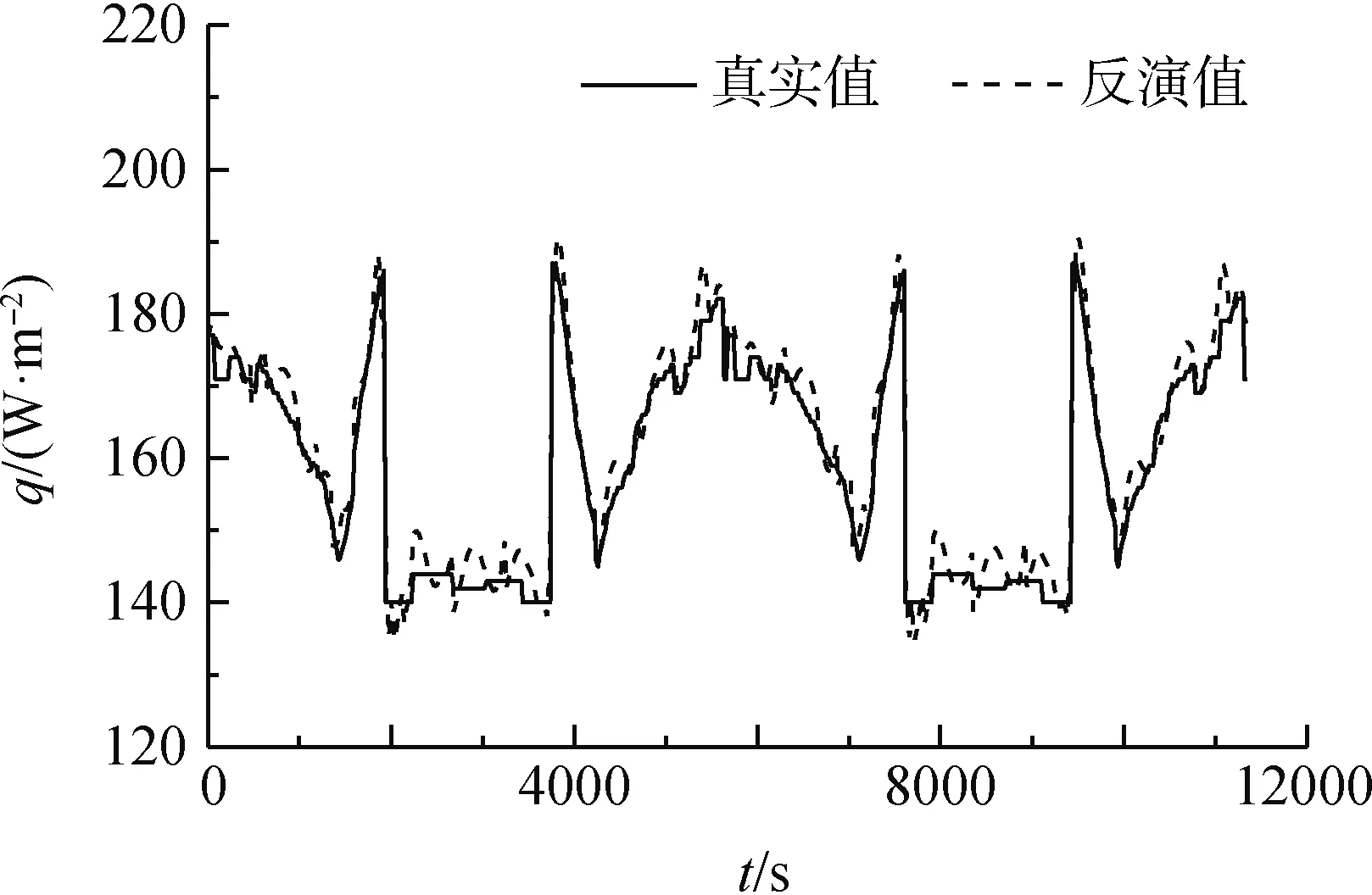
图7 qk,τ1～τ1+Δτ反演值与真实值比较

图8 qc,τ1～τ1+Δτ反演值与真实值比较

图9 qk,τ2～τ2+Δτ导热反问题反演值与真实值比较

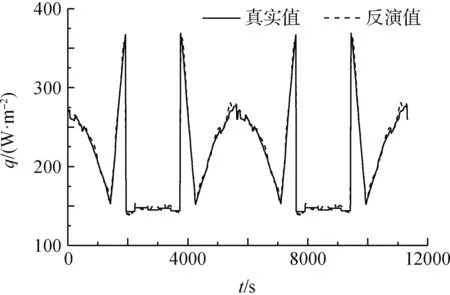
图10 qc,τ2～τ2+Δτ导热反问题反演值与真实值比较

4 结束语

本文介绍了一种利用卫星在轨温度数据计算热控涂层在轨性能退化情况的方法，建立并推导了适用于研究热控涂层随整数年变化规律的数学模型，该模型利用卫星设备的温度曲线通过反演计算得到设备表面热控涂层的退化数据。为检验数学模型的计算效果，构造了一组数值试验，先假设出热控涂层退化前和退化后的真实值，分别计算出不同热控涂层参数下卫星设备的温度曲线，然后采用本文模型对设备温度曲线进行反演计算，得到热控涂层退化数据，再与真实值比较。数值试验结果表明数学模型计算数据与真实值非常接近，说明本文建立的数学模型能够很好地根据卫星在轨温度计算出热控涂层在轨退化数据。

[1]闵桂荣,郭舜.航天器热控制[M].北京:科学出版社,1998:60-100.

[2]DONALD A J, GEORGE C T, DAVID T W, et al. Optical properties of thermal control coatings after weathering, simulated ascent heating and simulated space radiation exposure[R]. NASA 2008-215259.

[3]KRISTAN P G, RACHID D, GORDEN V. Reduced polarized thermal emission due to surface contamination by dew and atmospheric aerosols[J]. Journal of Quantitative Spectroscopy Radiative Transfer, 2004, 88(1):64-70.

[4]冯伟泉,丁义刚,闫德葵，等.地球同步轨道长寿命卫星热控涂层太阳吸收率性能退化研究[J].中国空间科学技术,2005,25(2):34-40.

FENG WEIQUAN, DING YIGANG, YAN DEKUI, et a1．Study on long-term degradation of solar absorptance properties of GEO stationary satellite thermal control coating[J].Chinese Space Science and Technology, 2005,25(2):34-40.

[5]刘宇明,冯伟泉,丁义刚.SR107-ZK在空间辐照下的物性变化[J].宇航材料工艺,2007,37(4):61-64.

LIU YUMING, FENG WEIQUAN, DING YIGANG. Space radiation effects on SR107-ZK[J]. Aerospace Materials & Technology, 2007,37(4):61-64.

[6]冯伟泉,丁义刚,闫德葵.空间电子、质子和紫外综合辐照模拟试验研究[J]. 航天器环境工程,2005,22(2):69-72.

FENG WEIQUAN,DING YIGANG, YAN DEKUI. Study on space electron, proton and ultraviolet combined irradiation simulation test[J]. Spacecraft Environment Engineering, 2005,22(2):69-72.

[7]冯伟泉,王荣,丁义刚.低能质子对卫星热控涂层太阳吸收率的影响[J].中国空间科学技术,2007,27(6):42-47.

FENG WEIQUAN, WANG RONG,DING YIGANG.Low energy proton effects on solar absorptance of thermal control coatings[J]. Chinese Space Science and Technology,2007,27(6):42-47.

[8]TAN H P, LUO J F, XIA X L. Transient coupled radiation and conduction in a three layer composite with semitransparent specular interfaces and surfaces[J].Journal of Heat Transfer, 2002, 124(3):470-481.

(编辑：杨婵)

《中国空间科学技术》编辑部新动向

为提高论文发表速度、缩短科研成果公布的时间，《中国空间科学技术》与 “中国知网”签署了优先数字出版协议，文章一经录用即可实行优先数字出版。

另外，从2016年第1期开始，本刊将采用双栏排版。同时，新的版式每篇文章中添加了卷、通讯作者、引用格式等信息，并参照国标 GB/T 7714-2015对参考文献的格式进行了修改，方便阅读、引用和检索。

Prediction on Performance Degradation of Thermal Control Coating Based on Satellite Temperature on Orbit

SONG Xin ZHANG Youwei LIU Zijun SI Dongbo

(Beijing Institute of Spacecraft System Engineering，Beijing 100094)

A method was proposed to predict the performance degradation of thermal control coating based on temperature data on orbit.A mathematical model which was constructed to study the degradation of thermal control coating performance spanning integer years was verified by numerical simulations. The calculation data meet the true value well, indicating that the mathematical model is valid.

Thermal control coating; Performance degradation; Numerical simulation;Inversion of telemetry data;Satellite

2015-02-01。收修改稿日期：2015-06-01

10.3780/j.issn.1000-758X.2015.06.005

宋馨 1986年生，2010年获北京航空航天大学人机与环境工程专业硕士学位。研究方向为航天器热控技术。