最小二乘法在复杂极值调节控制对象最优工作点的动态预估研究

李国强，刘永勤

(渭南师范学院数理学院，陕西渭南714099)

对于极值调节控制对象可用图1表示:

文献［1］提出对这种非线性极值特性可用一条二次曲线去逼近:

利用观测过的n组数据和最小二乘法可以得到一个回归曲线模型:

利用(2)式就可以求出使y=yMax的xM了，我们在文献［2－4］中提出了一种动态预估算法，解决了G(s)中n≥2的高阶极值调节控制系统的最优工作点的动态预估问题.在此基础上，我们进一步研究在极值调节控制对象具有高阶惯性环节特别是具有大时滞环节时提高预估最优工作点速度的动态预估方法.我们分几种情况分别予以研究.

1 控制对象仅具有高阶惯性环节时的动态预估算法

设极值调节控制对象线性部分的传递函数为:

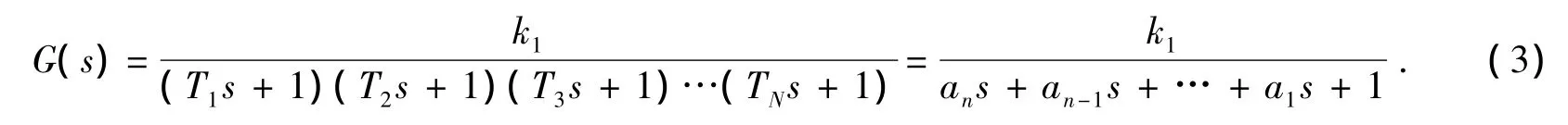
其中:an=T1T2T3…TN，a1=T1+T2+T3… +TN.

若T1＞＞T2≥T3≥…≥TN＞0，则可用一阶惯性环节与纯时滞环节的串联近似代替G(s).

其中:τ=T2+T3+… +TN.

步进式极值调节控制系统的系统框图可用图2表示，对Z(t)周期性采样的离散信号为z*(t)，经过变换与简化后图2可以变换为图3.

图2 步进式极值调节控制系统框图

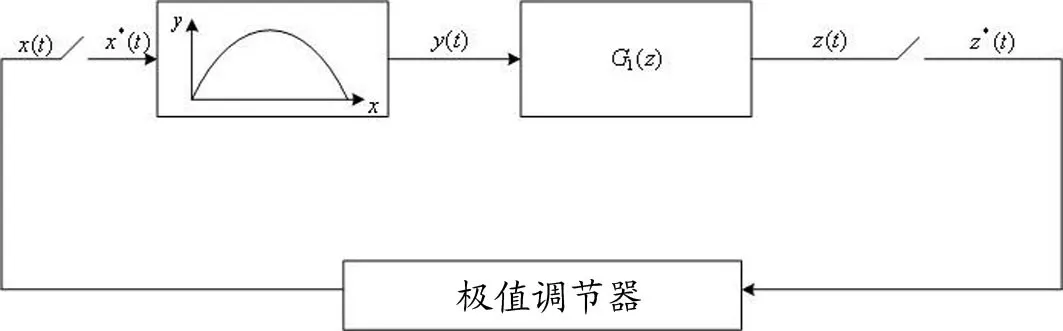
图3 简化后的系统框图

其中:

于是极值调节对象线性部分的数学模型为:［5－7］

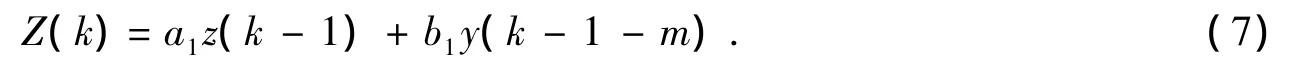
设附加在输出端Z(k)的噪声为e(k)，问题归结为m已知，利用观测序列X(k)，Z(k)，求出Y=YMax的XM把(1)式代入(7)式有:

令:b1r1=β1，b1r2=β2，则 (8)式可以表示为:

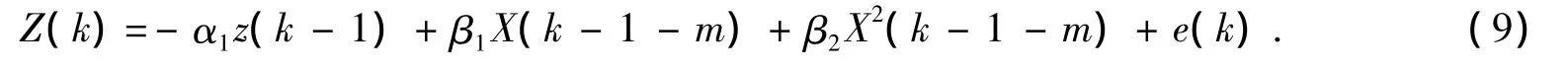
对(9)式可直接用最小二乘法估计出β1，β2.

由于

由(9)式及(2)式可得预估的最佳输入XM为:

2 控制对象同时具有大时滞环节与高阶惯性环节时的动态预估算法

设传递函数G(s)为:

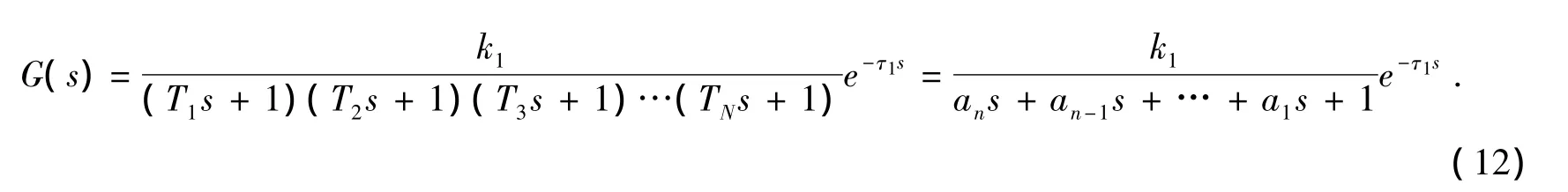
若T1＞＞T2≥T3≥…≥TN＞0，采用同样的思想方法，仍然可用一阶惯性环节与纯时滞环节的串联近似代替G(s).

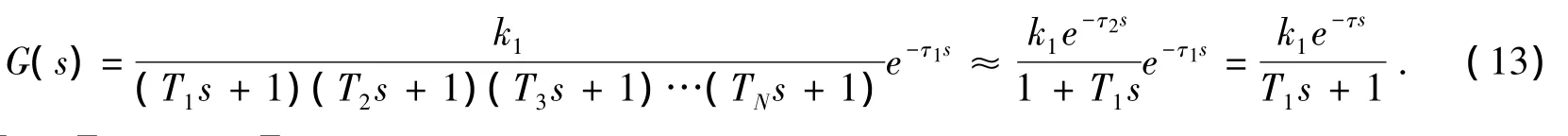
其中:τ2=T2+T3+… +TN;τ=τ1+τ2.

比较(13)式与(5)式可知，我们同样可以采用步进式极值调节控制系统，进行同样的方框图变换，用最小二乘算法求出预估的最佳输入XM，计算方法依然有效.

3 结论

对于极值调节控制对象，若G(s)表达式如(3)式所示，当T1＞＞T2≥T3≥…≥TN＞0，则可用一阶惯性环节与纯时滞环节的串联近似代替G(s)，用最小二乘法动态预估出极值调节控制系统的最优工作点.若控制对象同时具有大时滞环节与高阶惯性环节时，极值调节控制对象线性部分的传递函数的表达式如(12)式所示，若T1＞＞T2≥T3≥…≥TN＞0，我们仍然可用一阶惯性环节与纯时滞环节的串联近似代替G(s)，用最小二乘法动态预估出极值调节控制系统的最优工作点不仅计算简单，工作量小.

［1］王永初.最佳控制系统设计基础［M］.北京:科学出版社，1980.

［2］李国强，金轶锋，王存良.极值调节系统最优工作点预估研究［J］.陕西师范大学学报(自然科学版)，2002，(1):57－61.

［3］李国强，金轶锋.用最小二乘法动态预估极值调节对象的最优工作点［J］.现代电子技术，2001，(7):42－44.

［4］李国强.预估极值调节系统最优动态工作点仿真研究［J］.渭南师范学院学报，2003，(4):46－50.

［5］袁廷奇，刘文江.基于Hammerstein模型的自校正极值调节器［J］.仪器仪表学报，2001，22(4):413－415.

［6］夏绪辉.环缝磨的控制系统设计［J］.武汉科技大学学报，2002，(1):51－54.

［7］徐帆.基于自寻最优控制算法的谐波滤波器控制器［J］.变流技术与电力牵引，2007，(6):42－68.