Stability analysis of Alfvén eigenmodes in China Fusion Engineering Test Reactor fully non-inductive and hybrid mode scenarios

Wenjun YANG(杨文军),Guoqiang LI(李国强),Xueyu GONG(龚学余),Xiang GAO(高翔) and Xiaoe LI(李小娥)

1 University of South China,Hengyang 421001,People’s Republic of China

2 Institute of Plasma Physics,Chinese Academy of Sciences,Hefei 230031,People’s Republic of China

Abstract In this paper,NOVA/NOVA-K codes are used to investigate the stability of Alfvén eigenmodes(AEs)in the China Fusion Engineering Test Reactor(CFETR).Firstly,the stability of AEs excited by energetic alpha particles is investigated.For the fully non-inductive scenario,it is found that all AEs are stable,and the least stable toroidal mode number is n=8.However,for the hybrid mode scenario,it is found that many AEs are unstable,and the least stable toroidal mode numbers are n=7,8.Secondly,the effect of energetic alpha-particle parameters and beam ions on AE stability is also presented.The threshold of the least stable AE is about,less than the value of alpha-particle beta(βα=1.34%).The result demonstrates that the AEs excited by alpha particles are weakly unstable.The effect of the beam ions on AE stability is found to be very weak in CFETR.

Keywords:energetic particle,Alfvén eigenmode,NOVA/NOVA-K,CFETR

1.Introduction

The China Fusion Engineering Test Reactor(CFETR)is the next device in the roadmap for the realization of fusion energy in China[1,2],aiming to fill the gap between ITER[3]and DEMO[4].Significant success has been achieved in the engineering and physics design of CFETR during the past few years[5-7].In the meantime,for CFETR fusion plasma,many vital physical issues still have not been studied or understood.The stability of Alfvén eigenmodes(AEs),such as toroidal Alfvén eigenmodes(TAEs)[8],is one such issue.In the future of burning plasmas,both auxiliary heating and fusion reaction could generate energetic particles(EPs).On one hand,these EPs could heat the plasma via collisions with background ions and electrons.On the other hand,they also could excite various instabilities,such as energetic particle modes(EPMs)[9,10]and AEs[11-14].These instabilities could cause great alphaparticle loss,potentially destroying the first wall[15].Therefore,it is vital to investigate the characteristics of EPs and illuminate the effect of AE instabilities in CFETR.

In tokamak plasmas,the instabilities of AEs excited by EPs are very common[16-18].In the past several decades,both experimental and theoretical studies of AEs have been carried out[19-21].The linear stability of AEs driven by EPs has been investigated in ITER[22-26]and CFETR[8,18].Based on small-size parameters with minor radiusa=1.6 m,major radiusR=5.7 m andBT=5.0 T,the work shows that TAEs are almost all stable[8].Based on larger ones witha=1.8 m,R=7.0 m andBT=5.7 T,GEM code[27]was used to investigate the AE stability in CFETR,showing that AEs excited by energetic alpha particles are strongly unstable[18].There are obvious differences between the two works;thus,the stability of AEs needs to be widely investigated based on the latest CFETR parameters.

In this paper,the NOVA/NOVA-K codes[28,29]are used to investigate AE instabilities excited by EPs in CFETR.The linear characteristics of AEs have been investigated in tokamaks such as TFTR[30],JET[31]and DIII-D[32].Both the energetic alpha particles originated from fusion reaction and the beam ions generated from neutral beam injection(NBI)are considered in our study.Widespread linear simulations of AE instabilities have been carried out based on the latest CFETR parameters.First,it has been found that all AEs are stable and the least stable toroidal mode number is aboutn=8 for the CFETR fully non-inductive scenario(SCN).However,for the CFETR hybrid mode scenario(SCH)it is found that many AEs are unstable,and the most unstable toroidal mode numbers are aboutn=7,8.The excitation threshold of the least stable AE(n=8)is aboutβα0=1.12%,little less than the central alphaparticle beta(βα=1.34%).Second,the effect of the alphaparticle parameters and beam ions on AE instabilities is also presented in this paper.

Table 1.Plasma parameters for the CFETR SCN and SCH scenarios.

The paper is organized as follows:section 2 introduces the two different CFETR scenarios obtained through the integrated simulation.The stability analysis of the AEs for the CFETR SCN and SCH scenarios is shown in section 3.Section 4 gives the effect of the alpha-particle parameters and beam ions on AE instabilities.A brief discussion and summary are presented in section 5.

2.CFETR scenarios

Two different CFETR scenarios have been considered:SCN and SCH scenarios[33].The latest CFETR’s size is larger than ITER’s[3].The device isR=7.2 m anda=2.2 m in size,κ=2,δ=0.8 andBT(0)=6.5 T with a lower single null.Here we just consider the cases with the total fusion powerPf≈1000 MW.Table 1 shows the main plasma parameters for the two different CFETR scenarios.Pcdis the current drive power,andnbar/nGRis the ratio to Greenwald limit.SCN is a reversed shearqscenario,and auxiliary heating and current drive(H&CD)method is electron cyclotron wave(ECW)and NBI[34,35].SCH is a hybrid scenario,and the H&CD method is the combination of NBI,ECW,fast wave(FTW)[33]and/or low hybrid wave(LHW).Figure 1 shows the plasma equilibrium profiles of the relevant quantities.

The energetic alpha-particle distribution in velocity space is an isotropic slowing-down distribution,and can be written as follows[36]

whereS0andτsare the alpha-particle source intensity and slowing-down time,vcandαvare the slowing-down critical velocity and the maximum of the EP velocity respectively.Both alpha-particle betaβαand beam-ion betaβNBwere calculated using ONETWO code[37].The alpha-particle beta profiles for the CFETR SCN and SCH scenarios are shown in figure 2.

3.Simulation results

The NOVA/NOVA-K codes are used to investigate AE stability in CFETR.The kinetic effect of EPs is dealt with based on the drift-kinetic equation.The codes could deal with various damping mechanisms,including electron and ion Landau damping,electron collisional damping,radiative damping and continuum damping,and the codes also include the effect of finite Larmor radius(FLR)and finite orbit width(FOW)[38].AEs instabilities excited by the alpha particles will be presented in this section.

3.1.Fully non-inductive scenario

We will first consider the case of SCN.Based on the equilibria and profiles shown in section 2,the calculation results for all AEs found in the TAE gaps are shown in figure 3 for the SCN scenario.The range of toroidal mode number is 1≤n≤12.Our calculations show that the middle-n modes are the least stable case,and the drive of the high-n modes decrease withnincreasing,thus it is reasonable that the range is limited ton≤12.γα/γdampmeans the ratio of EPs’drive to total damping.If the ratioγα/γdamp＞1,then AE is unstable.n=8 withthe driveγα/ω≈0.51%.The calculation result canbe explained asfollows.Theoretically,the drive is peaked atk⊥·Δorb～1[39-41],wherek⊥≈nq/rand Δorb≈m υ‖/eB.Because the minor radius and toroidal From figure 3(a)we can see that withnincreasing,the drive first increases and then decreases,and the peak drive occurs inn=8 TAE withγα/γdamp≈0.1is the least stable mode.The magnetic field in CFETR are relatively larger than those in present tokamaks,the least stable mode number tends to be more big.

From figure 3(b)it is found that all AEs are stable,and corresponding mode structure is presented in figure 4(c),which demonstrates that the dominant poloidal harmonics arem=32 andm=33.Figure 4 shows the mode structures for the least stable eigenmodes withn=6,7,8.In order to better understand the calculated mode structures,the shear Alfvén continuous spectra withn=6,7,8 are shown in figure 5.It can be seen that the dominant poloidal harmonics are pairs of two neighboring harmonics for these modes.Furthermore,the calculation results show that the mode locations and frequencies are located within TAE gaps.Thus,they are all TAEs.

Figure 1.Equilibrium profiles of(a)electron and ion temperatures,electron density and(c)safety factor for the CFETR SCN,(b)electron and ion temperatures,electron density and(d)safety factor for the CFETR SCH.The sqrt(Ψ)means the square root of normalized poloidal flux.

Figure 2.The alpha-particle beta profiles for the CFETR(a)SCN and(b)SCH.

The damping calculations mainly include the collisional damping,Landau damping and radiative damping.In order to illustrate the relative contributions of the three damping mechanisms,figure 6 shows the ratio of the three damping mechanisms for average fractional contribution over all modes versus toroidal mode number.From the figure,we can see that both the collisional damping and the radiative damping are the main damping mechanisms.

3.2.Hybrid mode scenario

For the case of SCH,the calculation results for all AEs found in the TAE gaps are shown in figure 7.The range of toroidal mode number is also 1≤n≤12.As shown in figure 7(a),withnincreasing,the drive from the energetic alpha particles first increases and then decreases,and the peak drive occurs inn=8.The calculation result shows that the peak drive isThe result isconsistent with the previous theoreticalanalysis.From fgiure7(b)it can beseenthatmanyAEs are unstable,and the most unstable modes are ann=7 reversed shear Alfvén eigenmode(RSAE)withγα/γdamp≈1.19and ann=8 TAE withγα/γdamp≈1.20.The corresponding mode structure withn=7 is shown in figure 8(a),which demonstrates that the poloidal harmonic withm=9 is dominant.The mode,shown in fgiure 9(a),is located inside the TAE gap and near theqminposition,which confirms that it is a RSAE[42].The corresponding mode structure with then=8 is presented in figure 8(b),which demonstrates that the dominant poloidal harmonics arem=11 andm=12.The mode location and mode frequency are located within TAE gap.Thus it is a TAE.

Figure 3.AE stability analysis for the CFETR SCN scenario.(a)Energetic alpha-particle drive(γα / ω)for all modes found in TAE gaps to toroidal mode number.(b)The ratio of energetic alpha-particle drive to total damping(γα /γdamp)for the modes in(a).For a given n,we have found many AEs in the TAE gaps and the different colors are used to differentiate these AEs.

Figure 4.Mode structures for the least stable eigenmodes with toroidal mode numbers n=6,7,8.ξψ=ξ·∇ψ/∣∇ψ∣means the component of the perturbed displacement in the direction.

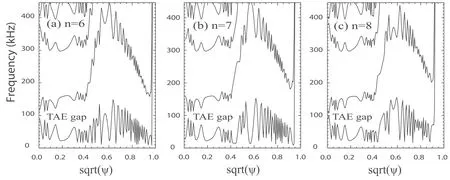
Figure 5.Alfvén continuum spectra of SCN with n=6,7,8.

Figure 6.Relative contributions of various dampings in SCN.The ratio of the three damping mechanisms for average fractional contribution over all modes versus toroidal mode number. γi is the respective damping and is normalized to the sum of all dampings.

For the case of SCH,the damping calculations also include the collisional damping,Landau damping and radiative damping.The ratio of the three damping mechanisms for average fractional contribution over all modes versus toroidal mode number is shown in figure 10.From the figure,we can see that the collisional damping is the main damping mechanism forn=1 to 12.

4.Effect of plasma parameters on AE stability

4.1.Effect of alpha-particle beta on AE stability

To see the sensibility effect of our profiles selection,we have investigated their effect on the AE stability for then=8 most unstable case for the CFETR SCH scenario.The plasma profiles shown in figure 1 are unchanged in our calculations,and the other plasma parameters are kept fixed when rescaling the alpha-particle beta.Based on the alpha-particle beta profile presented in figure 2(b),here it is just multiplied by a constant.Because the EP effects on the mode structure and frequency are neglected in NOVA-K code,the growth rate is linearly proportional to the energetic alpha-particle beta.We can obtain that the threshold for then=8 TAE is aboutβα0=1.12%,little less than the central alpha-particle betaβα=1.34%.

In order to study the effect of alpha-particle pressure gradient on the AE stability,the alpha-particle profile distribution has been changed but the central alpha-particle beta is fixed,which is shown in figure 11.The gradients are obviously different near the axis.The corresponding calculation results are presented in table 2.The total dampings are unchanged and there is little effect on the drive of energetic alpha particles for the three cases.The linear growth rate(γ)of TAE induced by alpha particles is written by[43].

whereωTAEandω* are the TAE eigenfrequency and the diamagnetic drift frequency of EPs respectively,fris the fraction of resonant particles,γdandqare the total damping and the safety factor respectively.Based on the drive term expression in equation(2),with the pressure gradient increasing,the valueω*(∝∂βα/ ∂r)will increase,thus the drive(γα/ω)will increase.However the decrease of the alpha-particle beta will make the drive decrease.The competition between the increase of the pressure gradient and the decrease of the alpha-particle beta makes the drive almost unchanged.On the contrary,with the gradient decreasing,the drive will decrease; however,the increase of the alpha-particle beta will make the drive increase.The competition between the decrease of the pressure gradient and the increase of the alpha-particle beta also makes the drive almost unchanged.Thus the growth rate is almost kept unchanged for the three cases.

Figure 7.AE stability analysis for the CFETR SCH scenario.(a)Energetic alpha-particle drive(γα / ω)for all modes found in TAE gaps to toroidal mode number.(b)The ratio of energetic alpha-particle drive to total damping(γα /γdamp)for the modes in(a).For a given n,different colors are used to differentiate the AEs.

Figure 8.Mode structures of dominant poloidal harmonics in direction for the most unstable eigenmodes.(a)n=7 RSAE with the dominant poloidal harmonic m=9.(b)n=8 TAE with the dominant poloidal harmonics m=11 and m=12.

4.2.The effect of the beam ions on AE stability

Here we consider the case that the beam ions with energyENB=500keV are injected on-axis in the CFETR SCH scenario.The species of the beam ion is deuterium.The beam ions have a slowing-down distribution in velocity space and are distributed exponentially in pitch angle

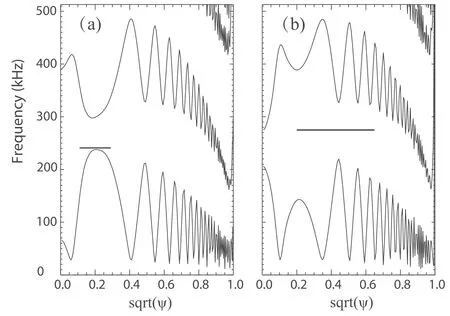
Figure 9.Alfvén continua for(a)n=7 and(b)n=8.The dark lines indicate the mode positions and mode frequencies.

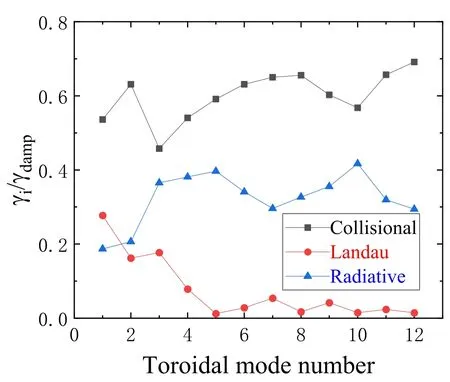
Figure 10.Relative contributions of various dampings in SCH.The ratio of the three damping mechanisms for average fractional contribution over all modes versus toroidal mode number γi is the respective damping.

wherecis a normalization factor,His the step function,υ0is the beam particle injection speed,andυcis the critical velocity given by

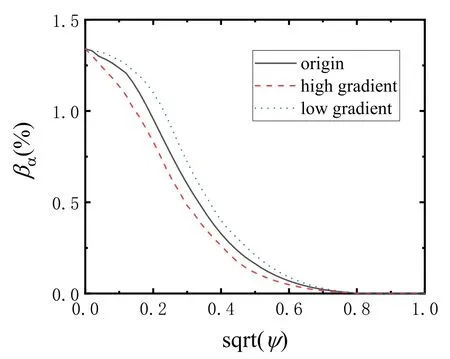
Figure 11.Three different alpha-particle beta profile distributions in thedirection for the origin beta,high gradient beta and low gradient beta.

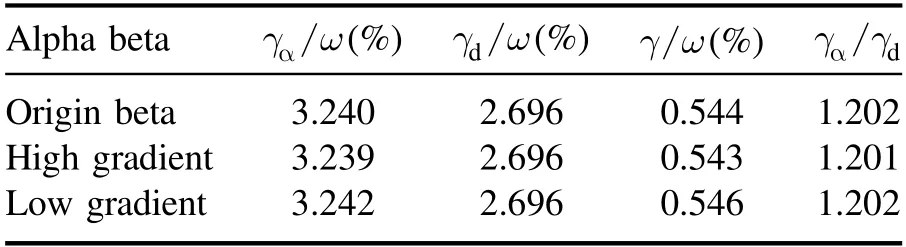
Table 2.Drive and total damping for the three cases.

Figure 12.Alpha-particle and beam-ion beta profiles for the SCH scenario.

Table 3.Drive from the energetic alpha particles and beam ions.

Λ is the pitch angle parameter,Λ0=0.4,ΔΛ=0.2.The distribution of the beam ions in the radial direction is calculated using ONETWO code.The alpha-particle and beam-ion beta profiles are shown in figure 12.The other plasma parameters are fixed while investigating the effect of the beam ions on AE stability.The drive from the beam ions is aboutγNB/ω=0.02%,far less than the drive from the alpha particles for then=8 most unstable case.We also investigate the effect of beam-ion energy on the AE stability.The calculation results are shown in table 3.The selected energy range is about 200 keV to 600 keV.The drive from the alpha particles is kept unchanged in our calculations.We observe that whenENBincreases,the drive from the beam ions(γNB/ω)firstly increases,and then saturates at aboutENB=400 keV,and finally decreases.This is because the beam ions are sub-Alfvénic,the drive must mainly come from theVA/ 3resonance.

5.Discussion and summary

In this paper,the NOVA/NOVA-K codes are used to investigate the stability of AEs excited by EPs,based on the CFETR SCN and SCH scenarios.Firstly,the stability of AEs driven by the alpha particles is investigated.For the SCN scenario,it is found that all AEs are stable and then=8 TAE withγα/ω≈0.51%is the least stable mode.However,for the SCH scenario,it is found that many AEs are unstable,and the most unstable toroidal mode numbers are aboutn=7,8.The drive of then=8 TAE(γα/ω≈3.24%)is slightly bigger than that of then=7 mode.Because the minor radius and toroidal magnetic field in CFETR are relatively larger than those in present tokamaks,the most unstable toroidal mode number tends to be bigger.

The effect of alpha-particle parameters on AE stability is presented.Because the growth rate is linearly proportional to the energetic alpha-particle beta in NOVA-K,the threshold is discovered to be aboutβcrit,α=1.12%,little less than the estimated value of alpha-particle beta(βα=1.34%)for then=8 most unstable case.The results demonstrate that AEs excited by the alpha particles are weakly unstable in CFETR,at least for the parameters presented in our work.However,in the work of Ren et al[18],the excitation threshold is aboutβcrit,α=0.2%,which is far less than our result.This can be explained as follows.Firstly,there is big difference in device parameters and profiles between our work and that of reference[18].Secondly,the model of reference[18]is non-perturbative and gyrokinetic whereas NOVA-K is perturbative and drift-kinetic model.Lastly,their model can not deal with the electron collisional damping,which turns out to be an important damping mechanism in our work.

The effect of the beam ions on AE stability is also presented.The drive from the beam ions is aboutγNB/ω=0.02%,far less than the drive from the alpha particles for then=8 most unstable case.The beam ions are mainly localized close to the axis(≈0.1); however,the TAE mode structure is mainly located around≈0.4.Thus the drive from the beam ions for this TAE is very weak.On the other hand,because the beam ions are sub-Alfvénic,the drive must mainly come from the less efficientVA/3 resonance.Thus the contribution of the beam ions is found to be very weak in CFETR.

The work aims to linearly investigate the stability of AEs excited by EPs in CFETR.The results demonstrate that all AEs found in TAE gaps are stable or weakly unstable for the two CFETR scenarios,and the effect of the beam ions is found to be very weak.These work will offer some guidance to reduce AEs instabilities for the CFETR design.However,non-linear simulations are needed to correctly evaluate effect of the EP transport on background plasma.To offer a more decisive guidance for the CFETR design,we will carry out self-consistent non-linear simulation in future work.

Acknowledgments

The authors would like to acknowledge Prof.G Y Fu for his suggestion and discussion.Numerical computations were performed on the ShenMa High Performance Computing Cluster in Institute of Plasma Physics,Chinese Academy of Sciences.This work was supported by National Natural Science Foundation of China(Nos.11947056 and 12005100),the Natural Science Foundation of Hunan Province(No.2020JJ5468),the Opening Project of Cooperative Innovation Center for Nuclear Fuel Cycle Technology and Equipment,University of South China(No.2019KFY15),the Hunan Nuclear Fusion International Science and Technology Innovation Cooperation Base(No.2018WK4009),and the Key Scientific Research Program of Education Department of Hunan Province(No.20A417).