基于反向学习的粒子群算法对线性相位低通FIR 滤波器的优化

邵 鹏，吴志健，周炫余

(1.武汉大学 软件工程国家重点实验室，武汉430072;2.武汉大学 计算机学院，武汉430072)

0 引 言

数字滤波器是数字信号处理系统中的重要组成部分。根据脉冲响应的长度，数字滤波器可以分为无限冲激响应(IIR)型和有限冲激响应(FIR)型。IIR 型数字滤波器可利用模拟滤波器进行设计，实现方法简单，但由于其在相频特性控制上是非线性相位，应用范围狭窄。FIR 型滤波器的相位是严格线性的，并且FIR 结构是非递归的，因此不存在稳定性问题。由于FIR 具有的这些特点，其应用越来越多。因此，设计高性能的FIR 数字滤波器显得尤为重要。

传统FIR 数字滤波器的设计方法有窗函数法［1］和频率抽样法［2-3］。这些方法都是近似的逼近理想滤波器的频率特征。频率抽样法和窗函数法简单易行，但不易精确地确定其通带和阻带的边界频率，并且都只能收敛于局部最优。近年来，学者们提出了使用演化算法，如模拟退火法(Simulated annealing algorithm，SAA)［4-5］、遗传算法(Genetic algorithm，GA)［6-7］、粒子群优化算法(Particle swarm optimization，PSO)［8-11］等进行数字滤波器设计并取得了很好的效果。但SA 算法采用了随机策略，运算量大［4］;GA 是一种全局优化算法，但采用了选择、交叉和变异等操作，运算量大、收敛速度慢［6］;PSO 算法也是一种全局优化算法，具有参数少、实现简单、收敛速度快等优点［11］，这对设计性能高的数字滤波器有很大的帮助。因此，本文将一种改进的粒子群算法应用于FIR 型数字滤波器的设计中，并通过仿真试验证明采用该算法所设计的滤波器有较好的滤波效果。

1 粒子群优化算法

1.1 算法概述

PSO 算法［11］最早是在1995 年由美国社会心理学家Kennedy 和电气工程师Eberhart 共同提出的，它是一种自适应群智能搜索算法，该算法思想源于对鱼群、鸟群等动物简单的捕食行为的模拟。PSO 算法的数学模型由速度更新方程和位置更新方程两部分组成。

速度更新方程如下:

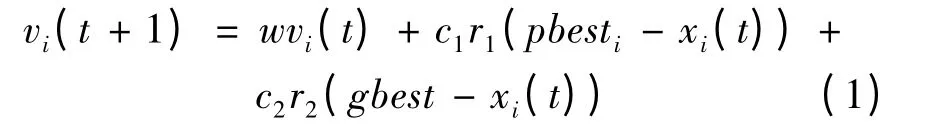
位置更新方程如下:

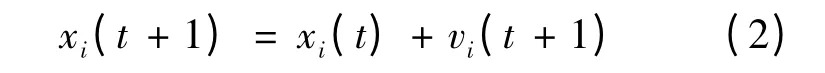
式中:vi(t+1)为粒子i 在第t+1 代的速度;xi(t+1)为粒子i 在第t+1 代的位置;c1和c2分别为认知系数和社会系数(加速因子);w 为惯性权重;r1和r2为［0，1］之间服从均匀分布的随机数;pbesti为第i 个个体历史最优位置;gbest 为群体历史最优化位置。

在PSO 算法中，每个粒子具有位置xi(t+1)和速度vi(t+1)两个参量，每个粒子代表搜索空间中一个候选解，粒子通过自身的经验值和其他粒子的经验值来调整自身的搜索策略。PSO 算法具有简单、容易实现、在初期收敛速度快但在后期很容易陷入局部最优、收敛速度慢且精度低等缺点［13］。

1.2 改进粒子群算法

1.2.1 反向学习策略

定义1［12］若x 是定义在实数集R 上区间［a，b］内的一个实数，即x ∈［a，b］，则x 的反向解x1定义如下:

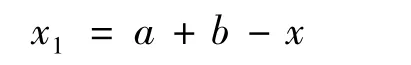
若a=0 且b=1，则有:

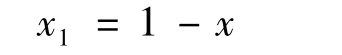
定义2［12］若P(x1，x2，…，xn)是n 维空间上的一个点，x1，x2，…，xn为实数，且xi∈［ai，bi］，则其反向解x 为:

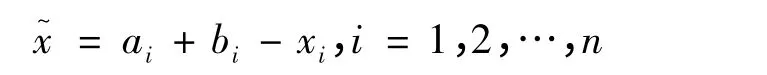
根据以上两个定义，反向学习算法思想描述如下:假设f(x)是原始函数，g(·)是评价函数。如果x 是区间［a，b］内产生的随机数，x1是x 的反向解，那么在每次迭代中计算f(x)和f(x1)，若g(f(x))≥g(f(x1))，仍然以x 进行迭代;否则以x1进行迭代。

反向学习策略是2005 年提出的智能学习策略，学者们已经证明该策略是一种有效的提高各种优化问题效率的方法［12］。

1.2.2 反向学习的粒子群算法(OPPSO)

为了克服粒子群优化算法存在的不足，引入反向学习策略来提高粒子群优化算法的优化性能。对于粒子群中的每一个候选解来说，通过反向学习策略计算每一个候选解的反向解，增加了候选解的个数，提高了种群的多样性，从而增加了找到全局最优解的概率。OPLPSO 算法描述如下:

(1) 随机初始化种群，初始化加速因子c1、c2，惯性权重ω 等参数;

(2) for i=1 to ps do

(3) 根据式(1)更新粒子的速度;

(4) if 速度不在规定的范围内

(5) 随机产生速度;

(6) 根据式(2)更新粒子的位置x;

(7) 计算粒子x 的适应值F;

(8) a=min(粒子位置);

(9) b=max(粒子位置);

(10)反向解x1=a+b－x;

(11)通过反向解x1计算适应值F1;

(12) if F1＜F

(13) x=x1;

(14) F=F1;

(15) 接下来同粒子群算法过程;

(16) end

2 FIR 数字滤波器

2.1 FIR 数字滤波器定义

FIR 滤波器［1］最重要的优点是其具有线性相位频率响应。FIR 滤波器的单位冲激响应h(n)是有限长的(0 ≤n ≤N－1)，其z 变换(系统函数)为:

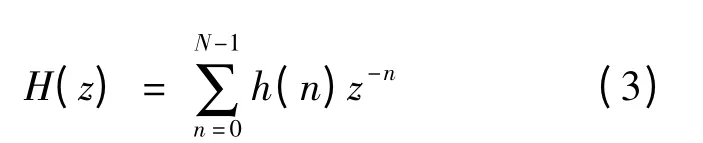
式中:N 为滤波器的阶数;h(n)为滤波器的脉冲响应，h(n)取值的不同决定FIR 滤波器的类型(低通、高通、带阻等)。

令z=ejω，则式(1)的频率响应可以转换为:

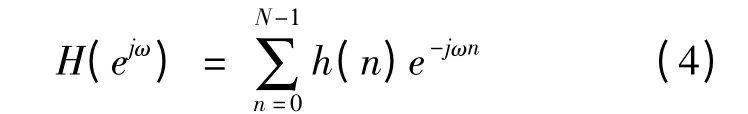
理想滤波器频率响应Hd(ejω)被分成相等的频率间隔，故可以得到:

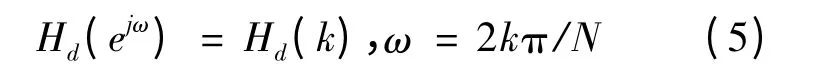
式中:Hd(k)为将要设计的滤波器的频率响应。当h(n)为实序列时，可将H(ejω)表示成:

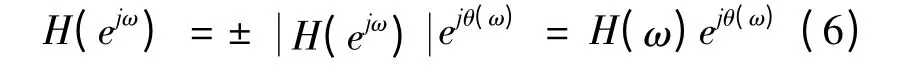
可证明FIR 滤波器有两类准确的线性相位［1］，其分别满足以下条件:

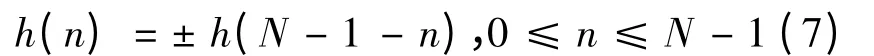
由式(7)可以看出:单位冲激响应的h(n)序列以n=(N－1)/2 为中心对称。因此，设计线性相位FIR 滤波器的计算量是设计非线性滤波器的一半。

FIR 滤波器的系统函数H(ejω)如式(3)所示，其中h(n)是FIR 滤波的n 个系数。这n 个系数取值的组合决定所设计FIR 滤波性能的好坏。

在OPPSO 优化FIR 滤波器的过程中，将n 个系数看作n 个粒子的位置。由于FIR 滤波器具有严格的线性相位，这种特性具有对称性，故在算法优化过程中只需要计算(n+1)/2 个粒子位置，也就是说只要找到n+1 个系数。

2.2 零相位低通FIR 滤波器

2.2.1 零相位数字滤波器

任何一个数字滤波器都具有幅频特性和相频特性，如果对于滤波不要求实时性，可以设计一种相频特性始终为0 的滤波器，即一个信号序列经过该滤波器滤波后，信号序列的相位不发生变化。这种数字滤波器就称为零相位数字滤波器［15］。零相位数字滤波器是为了使用一般的滤波器进行滤波时，由于滤波器的相位响应而导致待处理信号经过滤波器后产生的相位偏移进而产生相位失真而设计的［14-15］。

文献［15］中通过推导证明，零相位数字滤波器的设计思想简单，但只能通过软件来实现，靠硬件实现是相当困难、甚至是无法实现的。因此，零相位数字滤波器是一种更接近于理想的线性相位滤波器，即它也与现实中所设计的滤波器接近，更具参考性。正是由于它具有这种特性，文中将其作为理想滤波器与其他方法设计的滤波器进行比较，使这些滤波器逼近于理想的零相位数字滤波器。

2.2.2 低通FIR 数字滤波器

数字滤波器按频率特性可以分为低通、高通等类型［1］。低通滤波器(Low-pass filter)让低于所设计频率的信号分量通过，而对高于该频率的信号分量进行抑制，不让其通过。低通FIR 滤波器的性能要求通常以频率响应的幅度特性的允许误差来表征。频率响应有通带、阻带以及过渡带3 个范围。在通带内，频率响应逼近于1;阻带内逼近于0。为了逼近于理想的滤波器，在过渡带内的频率响应应该平滑地从通带下降到阻带，具体技术指标往往使用通带最大衰减(波纹)及阻带最小衰减。理想低通滤波器的频率响应见图1。

2.3 OPPSO 算法适应值函数

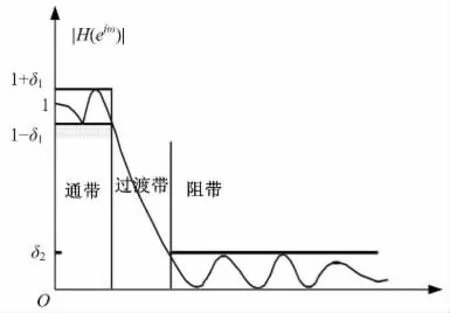
图1 理想低通滤波器的频率响应Fig.1 Ideal low-pass filter frequency response

目前设计FIR 滤波器有两种最优化准则:均方误差最小准则和最大误差最小化准则。已有研究［1］表明，第2 种准则设计出的滤波器在阶数相同时性能更优越。FIR 滤波器的主要优点就是能得到严格线性相位，因此文中所述的FIR 滤波器是指这类具有严格相位的滤波器。

设理想滤波器和所要设计的滤波器的频率响应的幅度函数分别为Hd(ejω)和H(ejω)，加权函数为G(ω)，则加权逼近误差函数定义为:

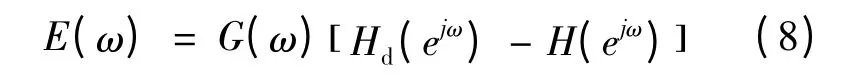
式中:G(ω)=δp/δs。

最小化误差函数:

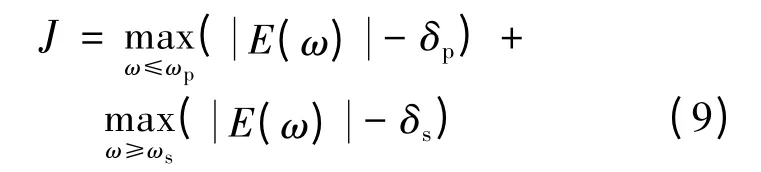
式中:δp、δs分别为通带和阻带波纹;ωp、ωs分别为通带和阻带的截止频率。

为了获得一组最优的滤波器系数，文中将式(9)作为OPPSO 算法以及与该算法相比较的算法的适应值函数，在文献［16-18］中此函数都作为适应值函数。用OPPSO 算法优化低通FIR 数字滤波器步骤如下:

Step1 给定低通FIR 滤波器的性能指标;

Step2 初始化OPPSO 算法各粒子的参数:种群大小、惯性权重等;

Step3 将滤波器系数作为粒子的初始位置并设粒子的初始速度;

Step4 根据式(10)计算粒子的适应值;

Step5 根据式(1)(2)更新粒子的速度和位置;

Step6 计算粒子的反向解，如果粒子原位置计算出的适应值比其反向解计算出的适应值大，则将反向解作为新的位置更新粒子的位置，否则用原位置更新粒子的位置;

Step7 判断是否更新粒子的个体极值pbest和粒子群的全局极值gbest;

Step8 重复(4)～(7)步直到满足精度要求或到达迭代次数为止;

Step9 输出gbest，得到最优化的FIR 数字滤波器的系数h(n)。

3 试验及结果分析

3.1 参数设置

为了验证所提算法设计FIR 滤波器的有效性，使用PSO 算法［8］、一种改进的PSO 算法(IPSO)［19］以及OPPSO 算法设计低通FIR 滤波器，并比较这3 种算法所设计的低通FIR 滤波器的性能。低通FIR 滤波器的频率响应为:

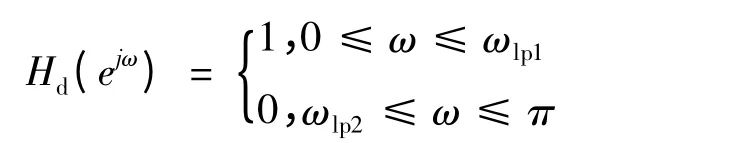
使用Matlab 语言实现算法以及FIR 滤波器的设计，所设计滤波器的阶数为40，即滤波器的系数的个数为41。滤波器的其他参数设置如下:通带波纹δp为0.1，阻带波纹δs为0.01;对于低通滤波器，其低通带截止频率ωlp1为0.25，低阻带截止频率ωlp2为0.35;过渡带宽度ωlp2－ωlp1为0.1。各种粒子群算法参数设置如表1 所示。

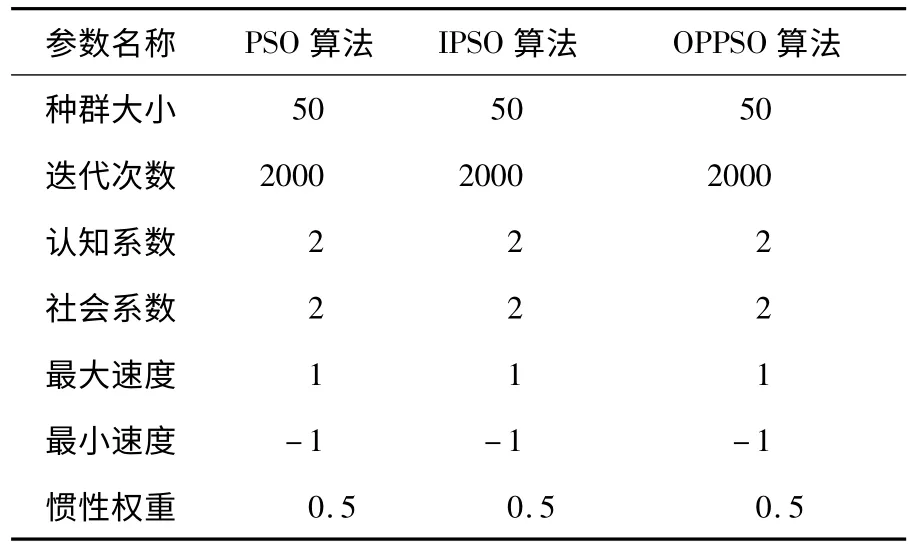
表1 粒子群算法参数设置Table 1 PSO parameter settings

3.2 试验结果及分析

3.2.1 低通FIR 滤波器设计结果

图2 为3 种算法所设计的低通FIR 滤波器的幅频响应，图3 为3 种算法的收敛速度曲线图。其中，H0为逼近于理想低通FIR 滤波器的零相位数字滤波器幅频响应曲线。

从图2(a)中可看出:由OPPSO 算法设计的低通FIR 滤波器的幅频响应更接近于文中设计的理想低通FIR 滤波器(零相位数字滤波器)，即其更平滑地从通带下降到阻带;通带波纹与零相位数字滤波器最接近，波纹波动较其他两种算法大。从图2 中可以看出:与其他算法相比，由OPPSO算法设计的低通FIR 滤波器的阻带衰减较小，更接近零相位数字滤波。综上所述，用OPPSO 算法所设计的低通FIR 数字滤波器的性能要高于其他算法所设计的滤波器性能。

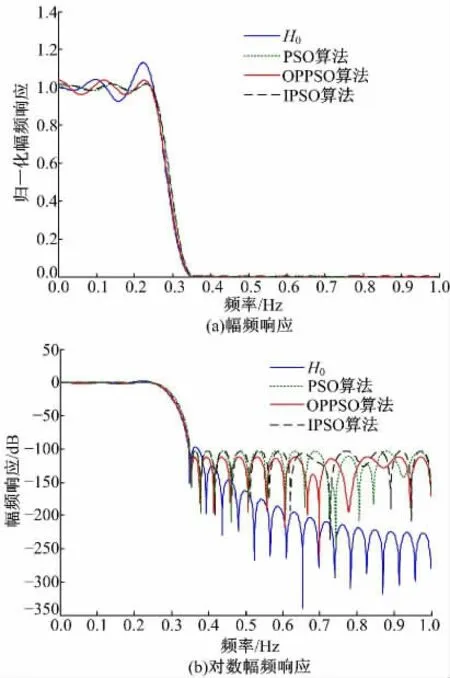
图2 FIR 低通滤波器幅频响应Fig.2 FIR low-pass filter amplitude-frequency response

3.2.2 三种算法收敛性分析

三种算法的收敛性如图3 所示。从图3 可以看出:OPPSO 算法比其他PSO 算法有着更快的收敛速度，并且收敛适应值最小，从而说明OPPSO算法能更快地找到一组相对最优的低通FIR 滤波器的系数。

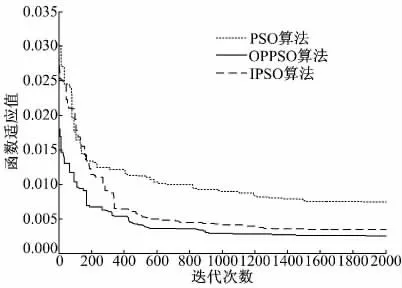
图3 三种PSO 算法收敛曲线图Fig.3 Converges of graph three algorithms

PSO、IPSO 和OPPSO 三种算法分别得到的低通FIR 滤波器系数的最优组合如表2 所示。

表2 三种算法最优系数组合Table 2 Optimal combination coefficient of three algorithms

从以上试验结果可以看出，OPPSO 算法在设计具有线性相位的低通FIR 滤波器方面比其他PSO 算法有着更好的性能。

4 结束语

为了验证OPPSO 算法所设计的具有线性相位FIR 低通滤波器的有效性，将其与PSO 算法以及IPSO 算法所设计的低通FIR 滤波器进行比较。同时，文中引入一种接近于理想数字滤波器、但很难使用硬件实现的零相位数字滤波作为对比。试验结果表明:OPPSO 算法在优化具有线性相位的低通FIR 滤波器时收敛速度快、收敛精度高，并能更快地获得一组最优的滤波器系数组合。因此，利用该算法可以设计出性能很好的低通FIR 数字滤波器。

［1］Li K，Liu Y.The FIR window function design based on evolutionary algorithm［C］∥2011 International Conference on Mechatronic Science，Electric Engineering and Computer，Jilin，2011:1797-1800.

［2］程佩青.数字信号处理［M］.北京:清华大学出版社，2009.

［3］Zhao Z K，Gao H Y，Liu Y Q.Chaotic particle swarm optimization for FIR filter design［C］∥2011 International Conference on Electrical and Control Engineering，Yichang，2011:2058-2061.

［4］Ahmad S U，Antoniou A.A genetic algorithm approach for fractional delay FIR filters［C］∥IEEE International Symposium on Circuits and Systems，Island of Kos，2006:2517-2520.

［5］Mastorakis N E，Gonos I F，Swamy M N S.Design of two dimensional recursive filters using genetic algorithms［J］.IEEE Transaction on Circuits and Systems-I:Fundamental Theory and Applications，2003，50(5):634-639.

［6］Mercier P，Kilambi S M，Nowrouzian B.Optimization of FRM FIR digital filters over CSD and CDBNS multiplier coefficient spaces employing a novel genetic algorithm［J］.Journal of Computers，2007，9(2):20-31.

［7］An-xin Z，Ping L，Jian-jun L.The design of FIR filter based on APA genetic algorithms［C］∥2011 International Conference on Mechatronic Science，Electric Engineering and Computer，Jilin，2011:1118-1121.

［8］李辉，张安，赵敏，等.粒子群优化算法在FIR 数字滤波器设计中的应用［J］.电子学报，2005，33(7):1338-1341.Li Hui，Zhang An，Zhao Min，et al.Particle swarm optimization algorithm for FIR digital filters design［J］.Acta Electronica Sinica，2005，33(7):1338-1341.

［9］Rajib Kar，Durbadal Mandal，Sangeeta Mondal，et al.Craziness based particle swarm optimization algorithm for FIR band stop filter design［J］.Swarm and Evolutionary Computation，2012，7:58-64.

［10］Mondal S，Chakraborty D，Kar R，et al.Novel particle swarm optimization for high pass FIR filter design［C］∥2012 IEEE Symposium on Humanities，Science and Engineering Research，Kuala Lumpur，2012:413-418.

［11］Kennedy J，Eberhart R.Particle swarm optimization［C］∥Proceedings of IEEE International Conference on Neural Networks，1995，4(2):1942-1948.

［12］Tizhoosh H R.Opposition-based learning:a new scheme for machine intelligence［C］∥CIMCA/IAWTI，Vienna，Austria，2005:695-701.

［13］寇晓丽，刘三阳.基于模拟退火的粒子群算法求解约束优化问题［J］.吉林大学学报:工学版，2007，37(1):136-140.Kou Xiao-li，Liu San-yang.Particle swarm algorithm based on simulated annealing to solve constrained optimization［J］.Journal of Jilin University(Engineering and Technology Edition)，2007，37(1):136-140.

［15］纪跃波，秦树人，汤宝平.零相位数字滤波器［J］.重庆大学学报:自然科学版，2000，23(16):4-7.Ji Yue-bo，Qin Shu-ren，Tang Bao-ping.Digital filtering with zero phase error［J］.Journal of Chongqing University(Natural Science Edition)，2000，23(16):4-7.

［16］Luitel B，Venayagamoorthy G K.Differential evolution particle swarm optimization for digital filter design［C］∥2008 IEEE Congress on Evolutionary Computation，Hong Kong，2008:3954-3961.

［17］Ababneh J I，Bataineh M H.Linear phase FIR filter design using particle swarm optimization and genetic algorithms［J］.Digital Signal Processing，2008，18(4):657-668.

［18］Sarangi A，Mahapatra R K，Panigrahi S P.DEPSO and PSO-QI in digital filter design［J］.Expert Systems with Applications，2011，38(9):10966-10973.

［19］Mandal S，Ghoshal S P，Kar R，et al.FIR band stop filter optimization by improved particle swarm optimization［C］∥2011 World Congress on Information and Communication Technologies，Mumbai，2011:699-704.