履带式移动机械臂的自适应模糊滑模控制

陈 杰，莫 玮

(1.西安电子科技大学 机电工程学院，西安710071;2.长江计算机(集团)公司 研发中心，上海200001)

0 引 言

非完整移动机械臂作为典型的非完整控制系统，其轨迹跟踪控制问题一直受到广泛关注［1-3］。在实际的应用过程中，移动机械臂内部或者外界总是存在一些不确定干扰因素，如外界扰动、机械臂本体的摩擦、振动、强惯性、非线性等因素，使得其控制系统的控制精度低、稳定性和可靠性差，无法完全满足工业生产的高精度、高可靠性要求。

传统单一的控制方法难以解决机械臂系统的这些问题。滑模控制能够增强机器人系统抗干扰能力，对系统的不确定性和外部扰动具有完全的自适应性。滑模控制的思想是反向控制，而反向控制的特性是具有强制性和很强的鲁棒性。因此，滑模控制应用于机械臂系统的控制成为学者们的研究热点［4-7］。然而，滑模控制在机械臂系统的控制过程中可能会出现抖振，导致系统的稳定性减弱。因此，单纯的滑模控制方法难以满足复杂环境下机械臂控制系统的工作要求。此外，机械臂系统本体参数的不确定性以及实际的运行过程中存在摩擦和干扰，难以建立准确的动力学模型，而模糊控制不需要知道被控制对象的精确数学模型，从而非常适用于那些动态特性不易掌握、数学模型难以获取或变化非常显著的研究对象。将模糊逻辑与神经网络结合的模糊神经网络控制方法已经逐渐成为国内外智能控制领域研究的热点，如文献［8］研究了一类履带式移动机械臂的神经网络鲁棒自适应滑模控制方法。文献［9-10］采用模糊神经网络去逼近控制系统中的未知非线性函数，并结合李雅普诺夫稳定性理论来调节网络连接权，避免了使用大量的参数自适应律。

鉴于以上原因，本文提出了一种非完整移动机械臂的自适应模糊终端滑模控制方法。在结合自适应模糊控制和非奇异终端滑模控制方法的基础上，研究了一类具有非线性、不确定性复杂环境下的非完整移动机械臂的轨迹跟踪控制问题。通过模糊高斯基函数神经网络的非线性逼近能力，优化补偿常规方法在移动机械臂系统中难以解决的系统未知参数不确定性。应用Lyapunov 稳定性理论，证明了机械臂控制系统的稳定性。通过仿真试验，比较已有的鲁棒自适应控制结果表明，该控制方法具有良好的动、静态性能和优越性，是一种行之有效的控制方法。

1 系统模型

为了防止复杂环境下非完整移动机械运行时出现影响控制精度的打滑现象，建立了如图1 所示的非完整移动机械臂的动力学模型。该机械臂属于履带式的非完整移动机械臂、具有外部扰动，其动力学模型可描述为:

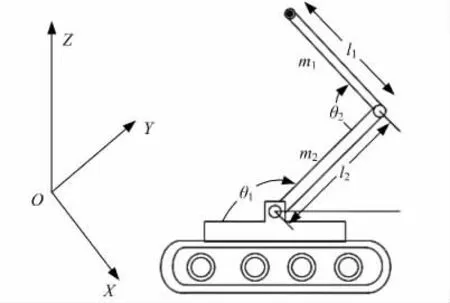
图1 履带式移动机械臂Fig.1 Crawler mobile manipulator

非完整约束可表示为:

取n－m 维满秩矩阵S(θ)为A(θ)的零空间的一组基，即有:

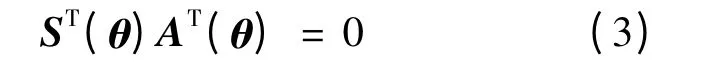
假设机械臂系统的期望轨迹为ηd∈Rn，跟踪误差为e=ηd－η，则选取如下的非奇异终端滑模面:

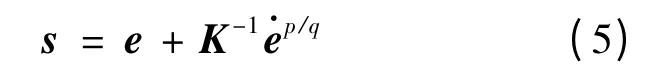
式中:K = diag{k1，k2，…，kn}，ki(i = 1，2，…，n);1 ＜p/q ＜2 均为常数。

对式(5)进行求导得:

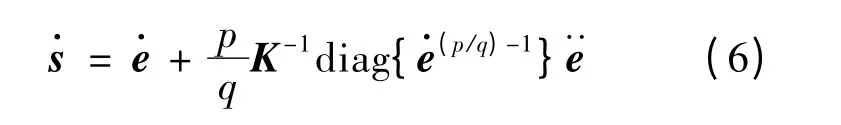
将式(5)和(6)代入(4)可得:

2 模糊高斯基函数神经网络

模糊高斯基函数神经网络(Fuzzy gaussian potential function neural networks，FGPFNN)是将GPFNN 网络和模糊系统结合起来的一种网络。其网络结构如图2 所示。

图2 FGPFNN 网络结构Fig.2 FGPFNN network structure

FGPFNN 网络结构分为4 层:第1 层为输入层，其作用是将特征向量x=［x1，x2，…，xn］T引入网络;第2 层为模糊化层，其作用是完成输入特征向量的模糊化，将输入量分为3 个等级{大(large)，中(medium)，小(small)}，其中隶属函数采用高斯函数exp(－［(x－m)/v］2)，m 为高斯函数的中心，v 为高斯函数的宽度;第3 层为模糊推理层，其目的是对模糊化后的特征向量进行综合处理;第4 层为输出层，对应的操作是去模糊化，用分类的序号表示输出节点。

根据模糊高斯基函数神经网络的结构和特点，知其输出变量为f=WTΓ(x，m，v)，Γ(·)为输出函数。由于非完整移动机械臂的动力学模型中包含有非线性未知项f(x)，因此，采用模糊高斯基函数神经网络来逼近未知项f(x)。即存在一个实值矩阵W*和实向量m*，v*使得下列等式成立:

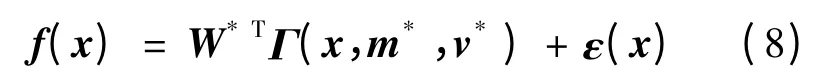
式中:ε(x)为有界的误差向量，且满足‖ε(x)‖≤εN。

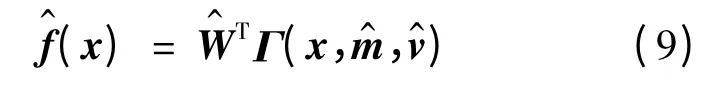
3 控制器的设计及稳定性分析

通过设计一个非奇异终端滑模控制器来控制移动机械臂系统，通过借助Lyapunov 定理来验证系统的稳定性。由于非完整移动机械臂系统中含有不确定函数项，于是通过上面介绍的模糊高斯基函数神经网络来补偿这些不确定函数项。从而，选取如下的控制律:

通过应用控制器，机械臂闭环系统可表示为:

为了简便，式(12)可表示为:

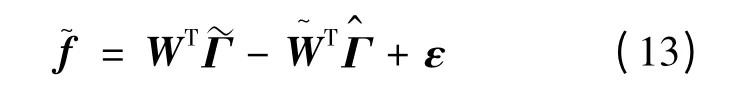
为了通过模糊高斯基函数神经网络来补偿这些不确定函数项，使用线性化理论将这些非线性模糊高斯基函数神经网络的输出转化成线性的形式。因此，将˜Γ 按泰勒形式展开有:

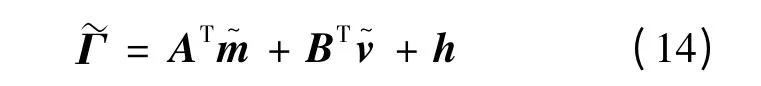
h 为一个有界的高阶无穷小向量。

将式(14)代入式(13)得:

为了验证本文的主要结果，引入如下假设:

假设1 假设模糊神经网络权值W，m 和v是有界的，即存在正常数Wd，md，vd，使得‖W‖≤Wd，‖m‖≤md，‖v‖≤vd。

假设4 假设矩阵A 和B 是有界的且分别满足关系式:‖A‖≤bA和‖B‖≤bB。

根据上面的假设，可以得知d 满足如下公式:

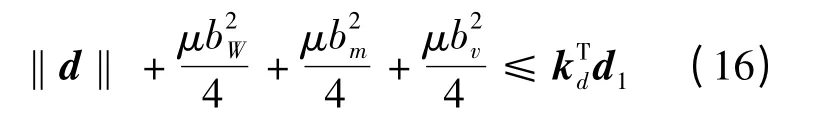
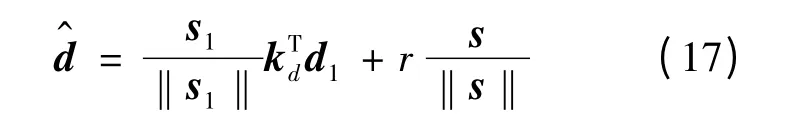
式中:r 为常数。

为了实现对非完整移动机械臂系统的自适应模糊滑模控制，本文得到了如下结果:

定理1 假设1 ～4 成立，如果非完整移动机械臂系统(见式(4))选取如式(10)的控制律以及式(17)所示的鲁棒项，并选取如下的神经网络权值更新率:

式中:KW，Km和Kv为正定对称矩阵;μ ＞0 为常数。则可以得到如下结论:

(2)所选取的控制器和控制律能够保证非完整移动机械臂系统(见式(4))的全局稳定性。

证明 考虑了如下的Lyapunov 函数:

将V 沿着系统(式(4))微分可知:

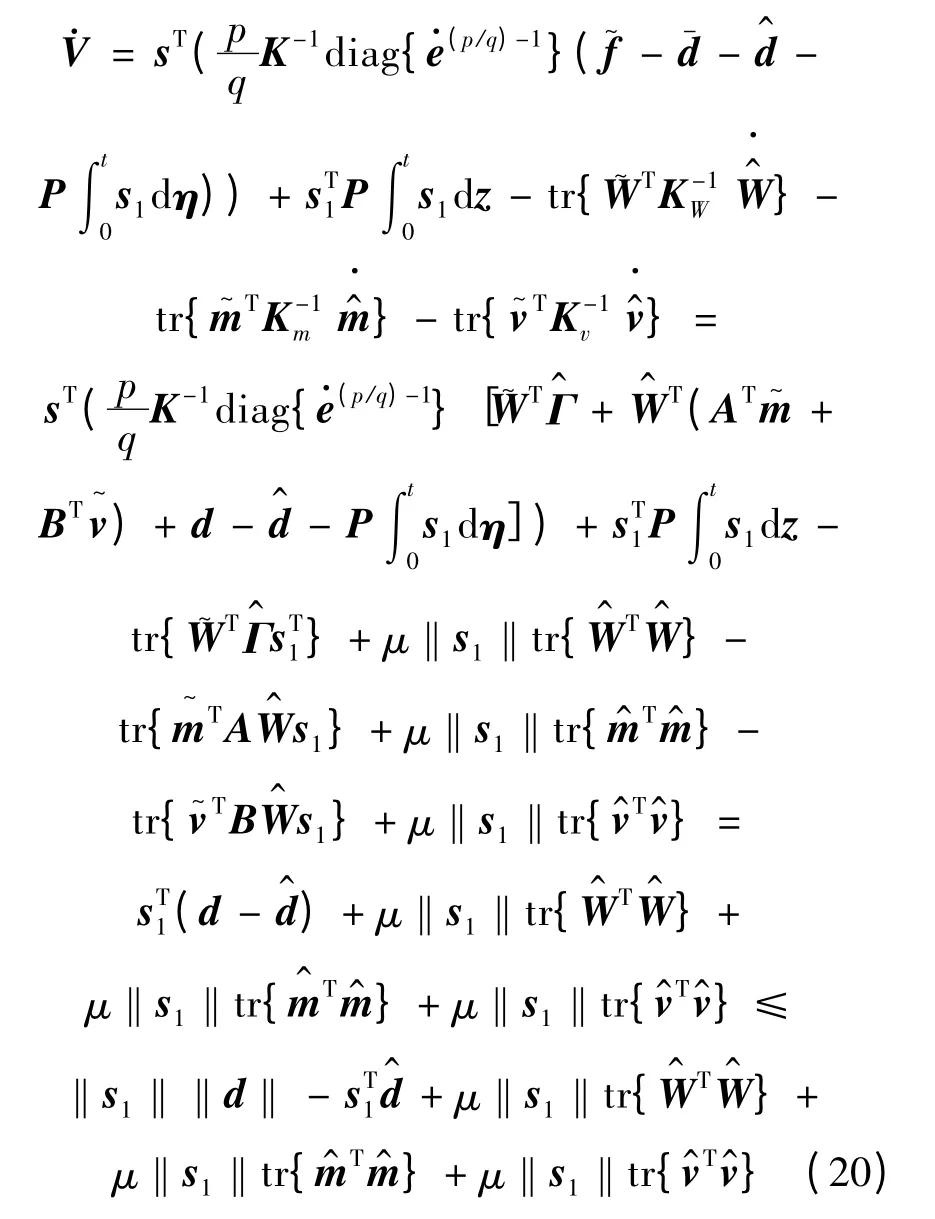
由定理1 所设计的非完整移动机械臂控制系统的框图如图3 所示。

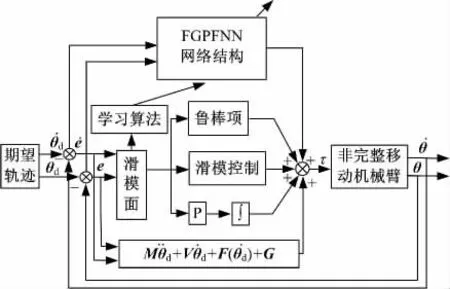
图3 移动机械臂控制系统框图Fig.3 Mobile manipulator control system block diagram

4 数值仿真

为了验证本文所提出的非完整移动机械臂的模糊高斯基函数神经网络的非奇异终端滑模控制方法，以如图4 所示的Motoman 机械臂为控制对

图4 Motoman 机械臂Fig.4 Motoman manipulator

象进行仿真试验。其运动学模型如式(1)所示，其中标称矩阵如下:

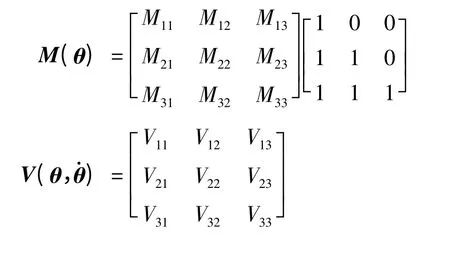
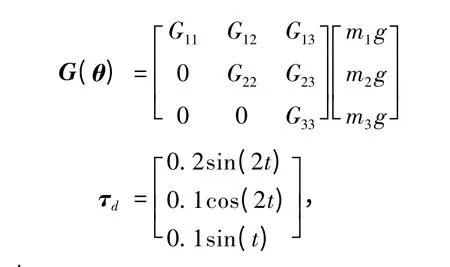
其中:

为了方便，选择非完整移动机械臂模型的控制参数如下:

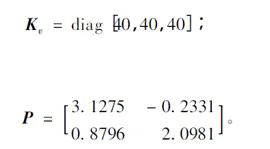
根据定理1，得知本文所提出的非完整移动机械臂的模糊高斯基函数神经网络的自适应模糊滑模控制器(AFSC)能够保证移动机械臂系统的稳定性。通过比较文献［8］的鲁棒自适应神经网络控制方法(RAC)，仿真结果如图5 所示，图5(a)～(c)为机械臂的轨迹跟踪曲线;图5(d)为机械臂的轨迹跟踪误差曲线。仿真结果表明:本文所设计的基于模糊高斯基函数神经网络的鲁棒自适应滑模控制方法能够较好地控制移动机械臂系统，圆满地实现了机械臂对于给定轨迹的跟踪控制。

图5 仿真结果Fig.5 Simulation results

5 结束语

研究了复杂环境下履带式移动机械臂的自适应模糊终端滑模控制问题。通过联合自适应模糊控制和非奇异终端滑模控制方法，研究了参数不确定性和外界扰动下非完整移动机械臂的轨迹跟踪控制方法。应用模糊高斯基函数神经网络的逼近能力来补偿移动机械臂系统中的不确定项，并采用非奇异终端滑模控制来消除系统的外界干扰和逼近误差对系统的影响，提高了系统的鲁棒性和动态性能。仿真试验中，通过比较常规的鲁棒自适应控制方法，验证了本文所提出方法的优越性和精确性，且对外界干扰具有很强的鲁棒性。

［1］胡立坤，马文光，赵鹏飞，等.六自由度机械臂的非奇异快速终端滑模控制［J］.吉林大学学报:工学版，2014，44(3):735-741.Hu Li-kun，Ma Wen-guang，Zhao Peng-fei，et al.Nonsingular fast terminal sliding mode control method for 6-DOF manipulator［J］.Journal of Jilin University(Engineering and Technology Edition)，2014，44(3):735-741.

［2］Liu Yu-gang，Li Yang-min.Sliding mode adaptive neural-network control for nonholonomic mobile modular manipulators［J］.Journal of Intelligent and Robotic Systems，2006，44(3):203-224.

［3］林雷，王洪瑞，任华彬.基于模糊变结构的机械臂控制［J］.控制理论与应用，2007，24(4):643-645.Lin Lei，Wang Hong-rui，Ren Hua-bin.Fuzzy based variable structure control for robotic manipulators［J］.Control Theory and Applications，2007，24(4):643-645.

［4］Chen S Y，Lin F J.Robust nonsingular terminal slidingmode control for nonlinear magneticbearing system［J］.IEEE Transactions on Control Systems Technology，2011，19(3):636-643.

［5］Chen M，Wu Q X，Cui R X.Terminal sliding mode tracking control for a class of SISO uncertain nonlinear systems［J］.ISA Transactions，2013，52(2):198-206.

［6］Man Z B，Paplinski A P，Wu H R.A robust MIMO terminal sliding mode control scheme for rigid robotic manipulator［J］.IEEE Transactions on Automatic Control，1994，39(12):2464-2469.

［7］Bayramoglu H，Komurcugil H.Nonsingular decoupled terminal sliding-mode control for a class of fourth-order nonlinear systems［J］.Communications in Nonlinear Science and Numerical Simulation，2013，18(9):2527-2539.

［8］Wang Yao-nan，Wu Xi-ru.Neural networks-based adaptive robust control of crawler-type mobile manipulators using sliding mode approach［J］.Industrial Robot，2012，39(3):260-270.

［9］Lin C K.Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks［J］.IEEE Transactions on Fuzzy Systems，2006，14(6):849-859.

［10］Efe M O.Fractional fuzzy adaptive sliding-mode control of a 2-DOF direct-drive robot arm［J］.IEEE Transactions on Systems，Man and Cybernetics，Part B，Cybernetics，2008，38(6):1561-1570.