康复机器人辅助站立人体质心动量测试及模拟

王志强，姜洪源，Roman Kamnik

(1.哈尔滨工业大学 机电工程学院，哈尔滨150001;2.卢布尔雅那大学 电气学院，卢布尔雅那1000，斯洛文尼亚)

0 引 言

对于有站立功能障碍的患者和下肢肌力不足的老年人站立是十分困难，甚至无法完成的动作［1］。站立过程需要人体的协调性和平衡能力，以及对身体重心的控制［2-3］。在站立过程中，人体重心投影区域将由坐姿时臀部和双脚的较大支撑面变为站姿时仅剩双脚的较小支撑面。站立运动是由关节力与力矩产生的加速度所控制，无法产生合适的重心加速度将导致站立过程人体质心动量控制差和无法保持身体平衡。所以，质心的位置、线性动量和角动量对于站立过程的平衡控制十分重要。因此，对于站立困难和肌力不足患者而言，需借助辅助器具完成站立过程。分析人体站立过程可知，身体各部位的运动学参数都对站立过程有影响，但人体重心是最重要的控制变量之一。虽然前期对于下肢各关节角度和各部分位移的测量已提供了部分数据可分析站立运动，但其作用是有限

的［4-5］。

辅助站立的方法是多样的，但目前辅助机器人已成为重要手段之一。而人体在不同的站立阶段其质心的位置、线性动量和角动量是变化的，可通过控制人体质心位置和动量来保持站立过程中身体的稳定性［6］。因此，需根据患者病情和站立状况设计合理的辅助机器人。但对人体在站立过程中的质心动量变化情况研究较少，特别是关于在使用特定的辅助器具时质心动量的研究。因此，本文对所设计［7］的康复机器人辅助人体站立过程中的重心动量和轨迹进行测试和建模，分析康复机器人在辅助人体站立过程中人体质心动量的变化，判断人体是否可以完成平稳的站立过程，通过对比模拟和测试结果判断所建模型的合理性。

1 起立机器人辅助人体站立过程人体质心动量和位置的数学模型

1.1 辅助起立机器人设计

所设计的辅助起立机器人具有水平、垂直滑动和矢状面内转动3 个自由度，其末端执行器在液压缸牵引下沿导轨做滑动，而导轨在液压缸驱动下做旋转运动，整个合成运动仅在矢状面内进行。同时为保证患者进行起立训练时的舒适性与安全性，设计了液压缸联动机构，其安装于自行车座和辅助机器人旋转关节处，使得车座转角与旋转关节所转角度相同，保证了患者跨骑于车座上始终保持水平位置［8］，所设计康复机器人如图1所示。

图1 康复机器人实物图Fig.1 Assistive standing-up robot

康复机器人采用的动力为液压系统，其可提供的最大压力为5 MPa，流量为1 L/s，因此末端执行器可达到的最大运动速度为2 m/s。液压系统与同马力电机和机械系统相比，体积小、承受压力大且成本低，通过液压软管传递动力，不受位置和形状限制并有自润滑作用。当液压系统超负荷时，可通过泄压阀进行控制，因此安全性较高。

1.2 站立过程人体质心动量建模

对人体站立过程的平衡能力进行分析可知，站立过程中通过增加质心动量来实现人体自主控制运动，通过减少动量来实现身体平衡的控制。质心动量是建立人体动力学与运动学关系的纽带，为定性分析站立过程的动力学变量提供了基础。

根据系统的拉格朗日动力学方程可建立康复机器人辅助人体站立时的质心动量数学模型，图2 为机器人辅助站立时的模型。对辅助人体站立过程做如下假设:①人体站立过程是两侧对称的;②站立过程只在矢状面内进行;③下肢各关节为无摩擦的铰接;④站立过程中上肢、躯干和头部视为整体。

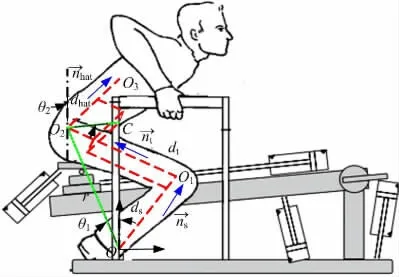
图2 辅助站立时人体质心轨迹与动量分析Fig.2 Analysis of trajectory and momentum of mass center during sit-to-stand by assistive standing-up robot

对系统的动能和势能求导可得拉格朗日方程为:

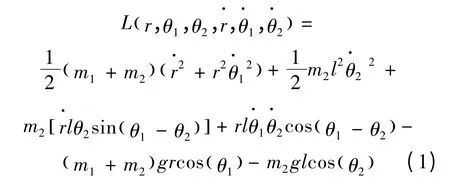
式中:m1为下肢的质量;m2为上肢、头部和躯干总的质量;l 为髋关节到质心的长度;θ1为OO2与垂直方向的夹角;θ2为OO3与垂直方向的夹角;r为踝关节与髋关节之间的可变长度，即OO2的长度随着站立过程是变化的。

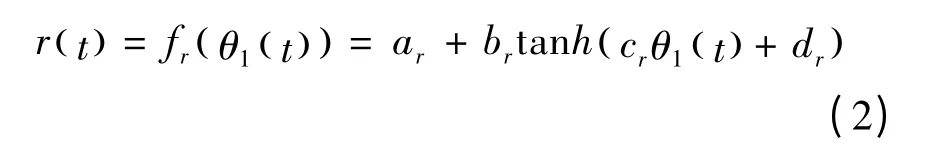
式中:ar=0.58;br=0.08;cr=4;dr=2。

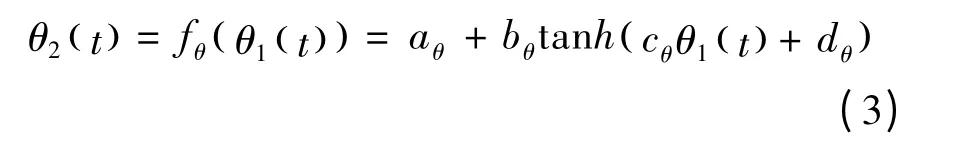
式中:aθ=0.25;bθ=0.25;cθ=4;dθ=2。

对式(2)(3)分别求导可得:

将式(4)(5)代入式(1)中可得:

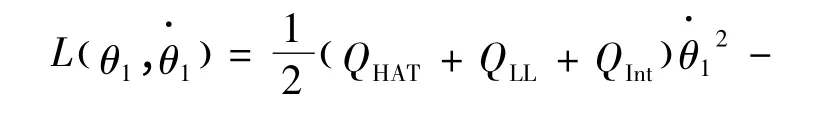
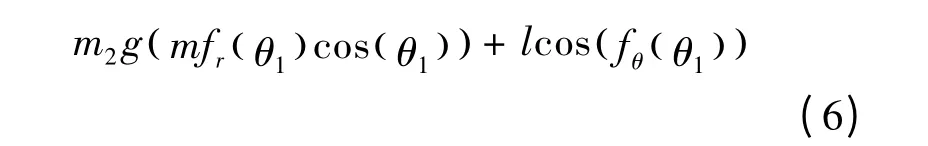
对系统拉格朗日方程(6)进行求导计算，可得出系统动量p 的公式为:

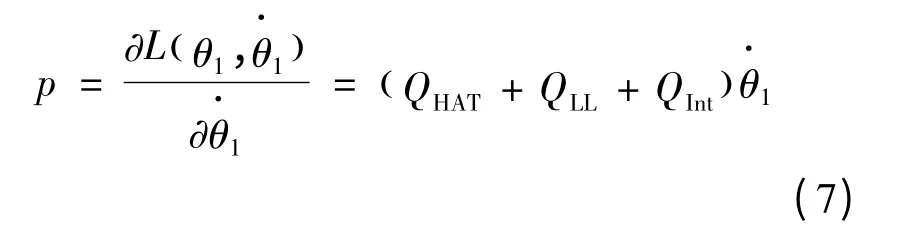
以式(7)作为人体质心动量的数学模型并进行仿真计算。

通过上述推导得出了人体在辅助站立过程中所受动量的数学表达式。此数学模型的建立为分析和模拟人体站立过程中重心动量的变化提供了理论依据。

1.3 站立过程人体质心轨迹建模

可使用辅助平行四边形法确定人体的质心位置，如图2 所示，将人体视为三连杆结构，即踝关节到膝关节的小腿部分，膝关节到髋关节的大腿部分和髋关节到身体重心处的上身部分，如图3所示。由图2 可得出踝关节点O 到人体重心C的矢量如式(8)所示，此矢量为人体站立过程的质心轨迹。

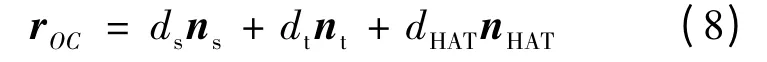
式中:ns、nt和nHAT分别表示沿小腿、大腿和上身(HAT)的单位向量;ms、mt和mHAT分别表示小腿、大腿和HAT 的质量(躯干、上肢和头);ds、dt和dHAT分别表示各部位尺寸和质量的影响因子:

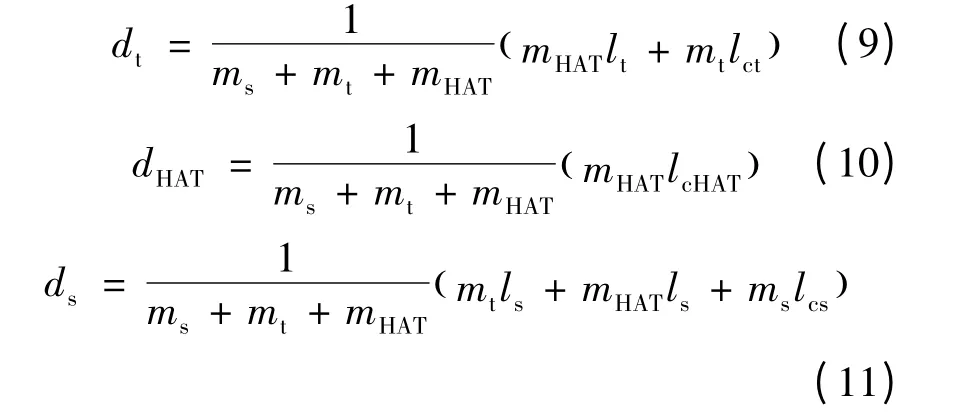
由人体测量学参数与所测角度的关系可求得站立过程中人体质心在水平和垂直方向的位置、速度和加速度表达式。人体质心在水手和垂直方向位置的表达式为:

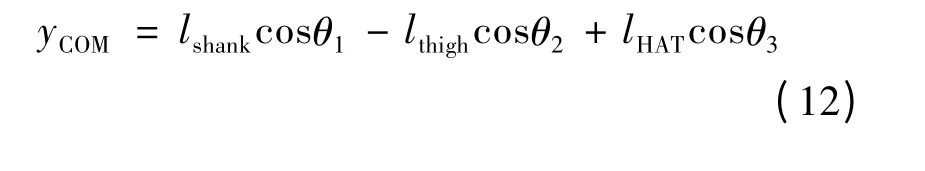
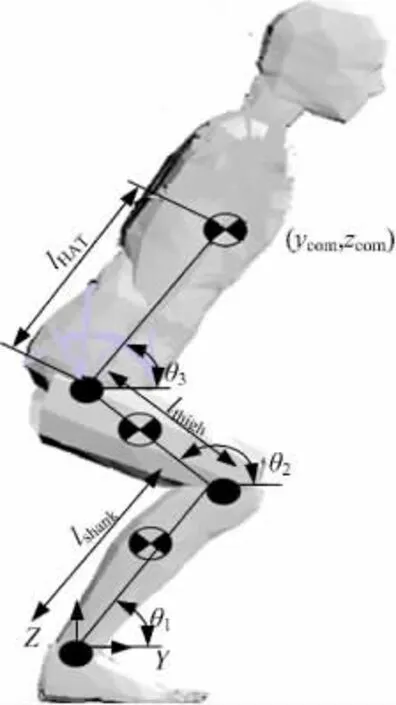
图3 人体站立的三杆模型Fig.3 Three segments model of human body during STS

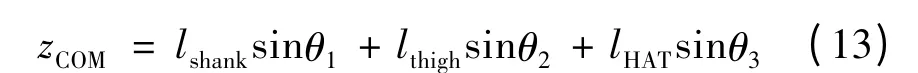
对式(12)(13)求导可得质心的速度公式为:

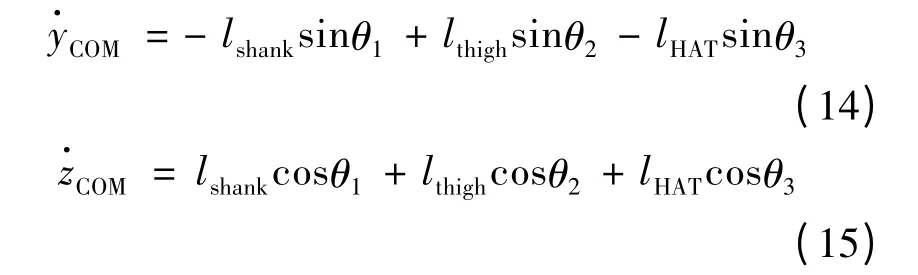
对速度表达式(14)(15)求导可得出人体质心在水平和垂直方向加速度的表达式为:

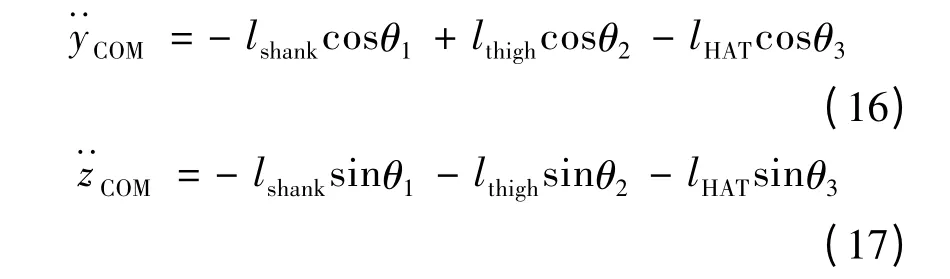
通过上述推导得出了人体站立过程中质心的位置、速度和加速度表达式，以上述表达式为基础可建立人体质心轨迹仿真模型的速度和加速度输入值。

2 辅助站立测试方法和设备

机器人辅助站立的主要目的是将人体重心由相对较低、受支撑的位置移动到直立、稳定的站立位置。跨骑于康复机器人末端执行器的测试者由液压系统驱动的机器人辅助躯干旋转，同时带动髋关节按所规划轨迹完成运动。在辅助站立过程中机器人运动关节将带动下肢伸展，使得身体质心在垂直和水平方向运动。为了完成站立，人体在机器人辅助站立过程中需要协调肌肉活动来实现对质心动量和下肢各部位运动的有效控制。对于不同的辅助站立速度，人体质心轨迹、线性动量和角动量的测试过程如图4 所示，其中，图4(a)为初始坐姿;图4(b)～图4(e)为辅助站立过程;图4(f)为完成站立。

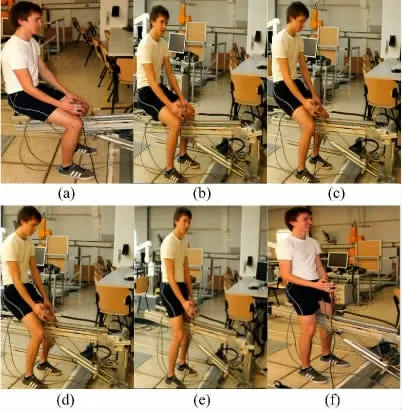
图4 康复机器人辅助起立测试过程Fig.4 Test process by assistive standing-up robot

测试过程中，先对测试者进行三次适应性训练，使其了解辅助机器人的运动特点和辅助站立的基本操作流程。测试者以自身最舒服的姿势跨骑于康复机器人上，主要测试设备包括:辅助起立康复机器人、高速摄像仪(加拿大NDI 公司的Optotrak Northern Digital Optical System 两台)、控制箱、笔记本宿主机(Host PC)和台式目标机(xPC)。宿主机安装所需软件，用于开发程序和建立模拟平台，而台式目标机用于监测和观察测试数据和图形。同时将红外线发光二极管标定点用双面胶粘贴于人体头部、躯干、髋部、手臂、大腿、小腿与脚部(即粘贴于小腿远端的外侧踝)，小腿近端腓骨头、大腿远端股骨踝、大腿近端大转子、髂骨、胸骨、肩关节、肘部上髁、腕关节和两眼间的山根。各红外线标定点与Stroker 插盒连接，而插盒将悬挂于腰带上。站立过程中Optotrak 三维光学运动分析系统的摄像仪对红外线标定点进行拍摄。由于布置于人体的红外线标定点数量较多，并同时对各关节和身体部位的运动信号进行采集和测试，因此可通过Optotrak 系统单元对所测多路数据信号进行信号同步处理。通过所设计的惯性传感器对人体动量进行测量，其安装位置依据人体测量学所确定。光学仪器测试的线性位置误差为±0.1 mm。

在对康复机器人辅助测试者站立过程中重心位置和动量变化进行模拟时，需要确定人体各部位的参数。在本文中，参与测试者为男性，年龄为23 周岁，身高为175 cm，体重为73 kg。人体各部位的参数如表1 所示［9］，其中下肢各部分转动惯量为矢状面内绕其质心的值。

表1 人体参数Table 1 Parameter of human body

3 测试及模拟结果

3.1 质心线性动量对辅助站立的影响

对机器人辅助站立过程中，慢速、常速和快速3 种情况时质心的动量进行了测试，并在Matlab/Simulink 中建立模拟平台对其进行模拟，如图5所示。

三种辅助站立速度情况下，动量总的变化趋势为由最小值逐渐增加到最大值，而后又逐渐减小。而模拟值与测试值曲线变化趋势一致，重合度较高，但模拟值与测试值之间也存在着波动和偏差，这是由于对所建人体模型进行简化造成的。对不同站立速度时质心动量进行测试结果可知，动量变化趋势较为相似，而幅值差别却较大，图5(a)为慢速站立时，其幅值测试值为30 kg·m/s，而模拟值为28 kg·m/s。图5(b)为常速辅助站立，其测试值为43 kg·m/s，模拟值为40 kg·m/s。而图5(c)为快速站立，其质心动量测试值为75 kg·m/s，模拟值为80 kg·m/s。采取不同辅助速度站立时，人体质心动量会发生较大变化，但康复机器人都能保证测试者既不发生摔倒又平稳地完成站立。

3.2 质心角动量对辅助站立的影响

对辅助站立过程中人体质心角动量进行测试，分析其在站立过程中的变化规律，测试的辅助速度分为慢速、常速和快速。图6 为不同辅助站立速度时人体质心角动量的变化曲线，快速站立时角动量的幅值(22 kg·m2/s)大于常速站立时(19 kg·m2/s)，而常速站立的角动量幅值大于慢速站立时的幅值(16 kg·m2/s)，当辅助站立速度由慢到快变化时，角动量幅值所对应横坐标的站立阶段百分比变小，说明质心旋转速度幅值前移，人体更早地进入站立阶段。

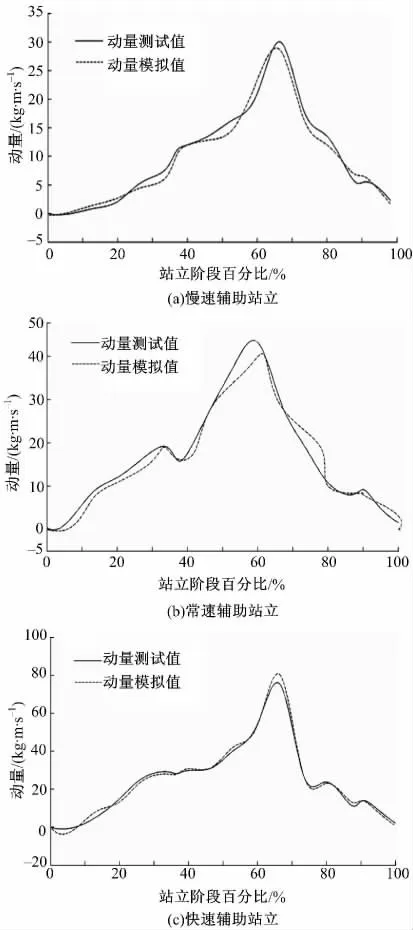
图5 辅助站立人体质心动量测试值和模拟值Fig.5 Experiment and simulation on body center-of-mass momentum of by assistive STS motion

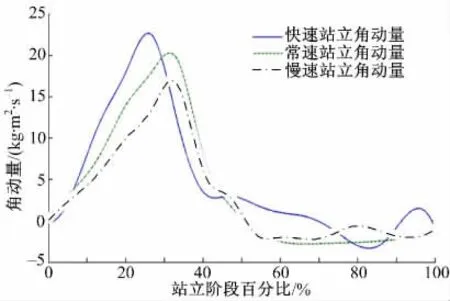
图6 辅助站立过程人体质心角动量Fig.6 Body center-of-mass angular momentum during assistive standing-up process

3.3 质心水平与垂直动量对辅助站立的影响

为了进一步分析机器人辅助站立过程中质心动量在水平和垂直两个方向对站立过程的影响，对水平和垂直动量进行测试和模拟，结果如图7所示。

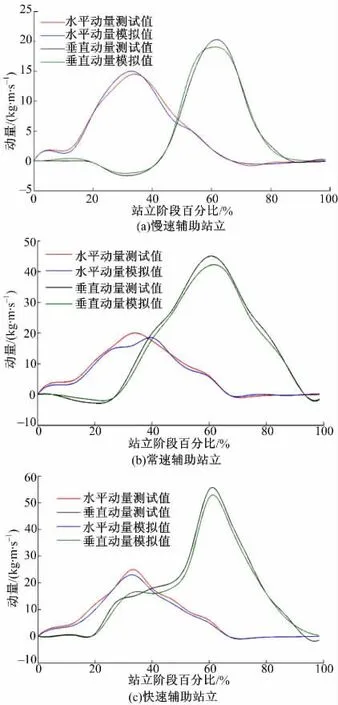
图7 辅助站立人体质心水平和垂直方向动量测试值和模拟值Fig.7 Experiment and simulation on body center-of-mass horizontal and vertical momentum during standing-up process

由图7 可知，慢、常和快速辅助站立时，水平动量峰值在站立过程中比垂直动量先产生，变化趋势为由小增加到最大值而后减小的过程。水平动量与垂直动量相比其幅值变化较小，而垂直动量幅值变化较大。由图7(a)可知:慢速辅助站立时水平动量幅值约为14 kg·m/s，当水平动量开始下降时，垂直动量开始增加，其幅值为20 kg·m/s。图7(b)为常速辅助站立，其水平动量幅值为20 kg·m/s，垂直动量幅值为43 kg·m/s，而图7(c)为快速辅助站立，其水平动量幅值为25 kg·m/s，垂直动量幅值为55 kg·m/s。对水平和垂直方向的站立动量进行模拟，模拟值与测试值可较好地重合，只在峰值处略有波动，因此所建模型可以较好地预测站立过程中水平和垂直方向动量的变化。

3.4 质心轨迹模拟及测试

对不同速度时康复机器人辅助人体站立的质心轨迹进行测试和模拟。将踝关节定为坐标原点，结果如图8 所示。

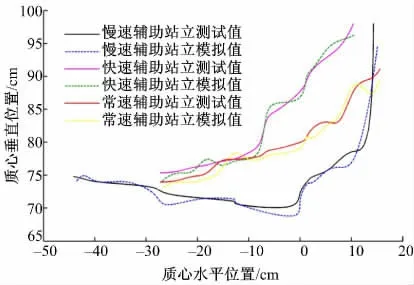
图8 辅助站立测试和模拟的质心轨迹Fig.8 Experiment and simulation on center-of-mass trajectory during assistive standing-up process

由图8 可知，慢速辅助站立时的质心轨迹在水平方向的位置变化相对于常速和快速时较大，表明人体质心水平位置的调整和身体弯曲程度较大，重心由开始阶段位于踝关节－45 cm 的位置移动到最终站立时的13 cm。而常速和快速辅助站立时人体对身体姿势的调整较小，质心相对于慢速辅助站立时更接近踝关节处。慢速辅助站立开始阶段时，质心在垂直方向的位置由75 cm 减小为70 cm，而后开始增加为98 cm，表明站立初期身体前倾导致质心垂直方向位置较小，而后伸展躯干完成站立，而常速和快速辅助站立过程中质心垂直方向位置始终保持增加，说明躯干没有前倾，而且快速站立过程垂直位置略大于常速站立。不同速度辅助站立过程中质心位置变化的模拟结果与测试结果较为相似，说明通过平行四边形法确定的质心位置可以较好地预测人体站立过程中的质心位置变化趋势。

4 结 论

(1)所设计的辅助机器人符合人体站立规律，既便于患者操作和参与辅助站立过程，又可平稳地辅助人体完成站立过程。

(2)采用不同辅助站立速度时，人体质心动量幅值变化较大，但患者都可平稳完成站立，模拟值与测试值略有偏差，但变化趋势一致，所建模型可有效地预测站立过程的重心动量。

(3)在不同速度辅助站立过程中，水平方向动量的幅值变化较小，而垂直方向动量幅值的变化较大。水平方向动量是既能保证患者不发生摔倒，又能平稳地完成站立的决定因素，而垂直方向动量是完成直立站立的决定因素。

(4)辅助站立速度增加时，会造成人体质心相对于踝关节位置前移，因此辅助站立时采用常速辅助对平稳站立更有利。辅助平行四边形法可以有效地预测站立过程中的质心轨迹。

［1］王志强，姜洪源，Roman Kamink.辅助起立机器人轨迹追踪仿真及试验研究［J］.医用生物力学，2013，28(2):171-177.Wang Zhi-qiang，Jiang Hong-yuan，Roman Kamink.Simulation and experimental study on trajectory tracking of the assistive standing-up robot［J］.Journal of Medical Biomechanics，2013，28(2):171-177.

［2］Scarborough D M，McGibbon C A，Krebs D E.Chair rise strategies in older adults with functional limitations［J］.Journal of Rehabilitation Research＆Development，2007，44(1):33-42.

［3］Neptune R R，McGowan C P.Muscle contributions to whole-body sagittal plane angular momentum during walking［J］.Journal of Biomechanics，2011，44(1):6-12.

［5］Flaxman T E，Speirs A D，Benoit D L.Joint stabilisers or moment actuators:the role of knee joint muscles while weight-bearing［J］.Journal of Biomechanics，2012，45(15):2570-2576.

［6］Kaya B K，Krebs D E，Riley P O.Dynamic stability in elders:momentum control in locomotor ADL［J］.Journal of Gerontology:Medical Sciences，1998，53(2):126-134.

［7］王志强.站立康复功能辅助机器人系统的控制及其关键技术研究［D］.哈尔滨:哈尔滨工业大学机电工程学院，2014.Wang Zhi-qiang.Control of the rehabilitative standingup robot system for sit-to-stand motion and research on key technology［D］.Harbin:School of Mechatronics Engineering，Harbin Institute of Technology，2014.

［8］王志强，姜洪源，Roman Kamink.辅助起立机器人反馈控制与速度前馈控制性能对比［J］.机器人学报，2012，34(6):641-645.Wang Zhi-qiang，Jiang Hong-yuan，Roman Kamink.Performance comparison on assistive standing-up robot with feedback and velocity feed-forward control［J］.ROBOT，2012，34(6):641-645.

［9］De Leva P.Adjustments to Zatsiorsky-Seluyanov＇s segment inertia parameters［J］.Journal of Biomechanics，1996，29(9):1223-1230.