基于PSO 算法和SVR 模型的加工中心可靠性模型参数估计

杨兆军，杨川贵，陈 菲，郝庆波，郑志同，王 松

(1.吉林大学 机械科学与工程学院，长春130022;2.吉林大学 机械工业数控装备可靠性技术重点实验室，长春130022;3.空军航空大学 飞行器与动力系，长春130022)

0 引 言

准确地对加工中心可靠性模型进行参数估计，有利于正确评估加工中心的可靠性水平，对加工中心制造企业实施可靠性增长具有重要的意义［1］。可靠性估计的准确程度与所选择的可靠性模型及其参数估计方法有关。已有研究结果表明，威布尔(Weibull)模型能较好地描述加工中心的可靠性分布，其准确性依赖于对分布参数的估计精度。在参数估计方面，常用的方法有最小二乘法(LSM)、最大似然估计(MLM)［2］和贝叶斯方法［3］。其中，前两种是基于经验风险最小原则发展起来的经典统计方法，但是在样本数量较少的情况下，上述方法很难获得可靠性模型的最优参数。贝叶斯方法在小样本实验数据条件下体现出其优势，但其估计精度取决于所选择的先验分布。支持向量回归(Support vector regression，SVR)模型［4］在小样本情况下有很好的归纳能力，与性能优越的优化算法进行耦合能得到比较准确的参数估计值。

目前为止，鲜有文献将支持向量回归模型用于可靠性模型的参数估计。为此，本文尝试将其用于估计加工中心可靠性模型的参数，并将其与本文提出的改进的局部最优粒子群优化算法(Improved local best particle swarm optimization，Improved lbest PSO)耦合，实现支持向量回归模型的参数优化。Improved lbest PSO 算法在局部最优粒子群优化算法(lbest PSO)的基础上引入了变异操作和自适应调整惯性因子，以抑制算法的早熟并提高算法的全局最优解搜索能力。

1 加工中心可靠性模型

加工中心是一种复杂的可修复系统。前期研究工作表明:威布尔模型能较好地描述加工中心的可靠性分布，同时加工中心的故障间隔时间是其可靠性水平的体现［5］。根据威布尔模型，加工中心故障间隔时间的密度函数(即故障密度函数)可用式(1)表示:

式中:λ 为比例参数;k 为形状参数。

同时，加工中心的故障分布函数和可靠度函数(即可靠性模型)分别如式(2)和式(3)所示:

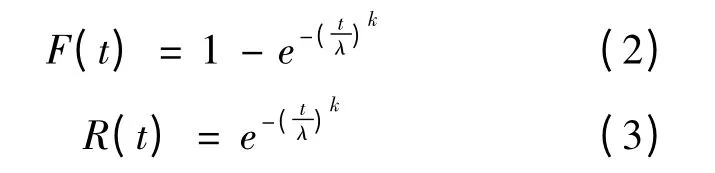
平均故障间隔时间(MTBF)是加工中心可靠性评价的重要指标之一，平均故障间隔时间越长，则加工中心越可靠。其计算公式为:

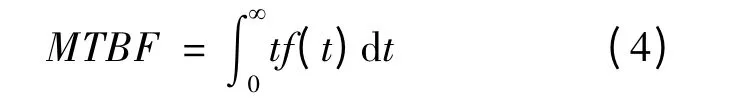
通过式(3)可以看出，加工中心可靠性模型的准确程度取决于其参数λ 和k 的估计精度。

2 可靠性模型参数估计方法

2.1 故障经验分布函数估计

为了估计可靠性模型的参数，需要对故障分布函数做出评估。假设加工中心提供了n 个故障间隔时间，依次为t1≤t2≤…≤tn，其中i 为故障间隔时间序号。当处理不完全数据时，平均秩次法［6］能够提供高精度的故障经验分布，因此本文采用该方法对故障经验分布函数进行计算。该加工中心的故障经验分布函数计算过程如下:

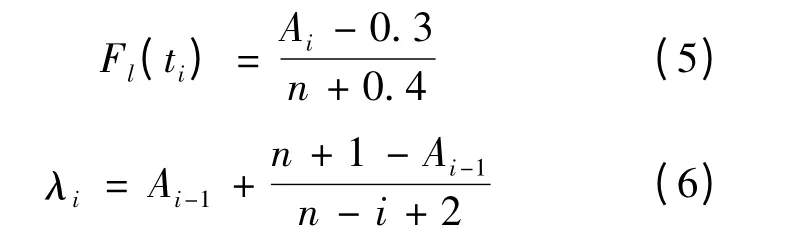
式中:Ai为第i 个故障的平均秩次，并且A1=1。

2.2 用于参数λ 和k 估计的支持向量回归模型

为了估计参数λ 和k，首先对式(2)进行线性化处理，得出如下等式:

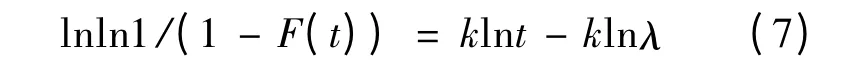
令y=lnln1/(1－F(t))，w=k，φ(x)=lnt，b=－klnλ，则式(7)可表示如下:

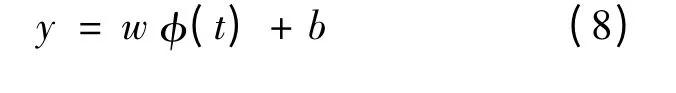
根据结构风险最小原则，SVR 模型通过对如下损失函数最小化以获得w、b 的估计值。根据文献［7-8］，用于估计参数λ、k 的支持向量回归模型如下:

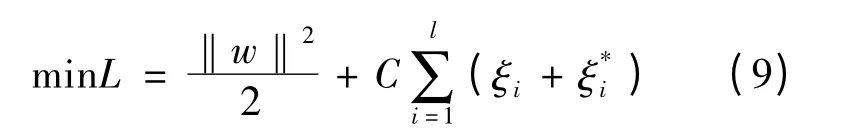
约束条件:

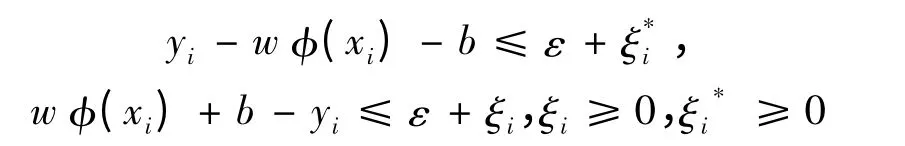
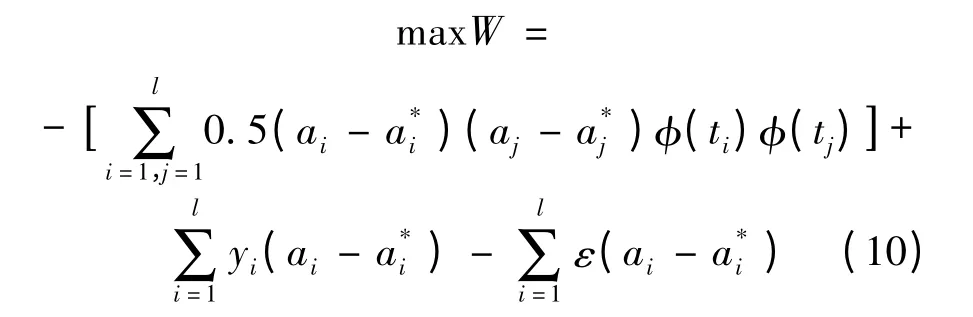
约束条件:

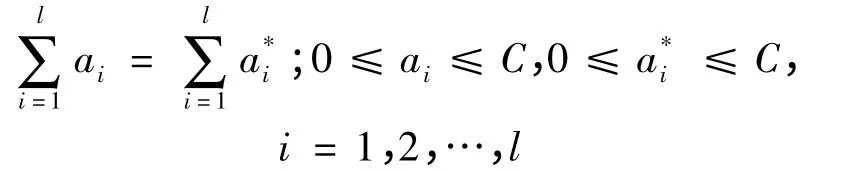
根据Lagrange 乘子法则，参数w 的计算公式如下:

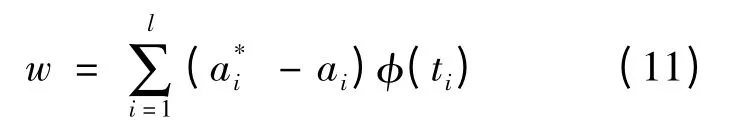
利用Karush-Kuhn-Tucker(KKT)［7］条件，参数b 可通过如下公式计算:

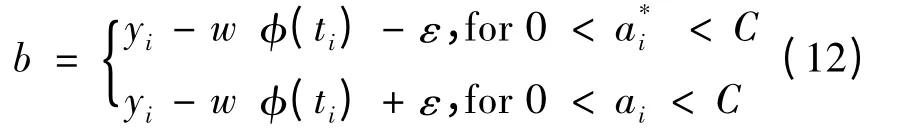
综上可知，式(3)中的参数可通过如下公式得出:

图1 描述了参数C 和ε 对SVR 模型精度的影响。由图1 可知，上述SVR 模型的估计精度完全受参数C、ε 的影响，因此SVR 模型的参数优化是其面临的首要任务。

2.3 支持向量回归模型参数优化

2.3.1 lbestPSO 算法概述

在本文中，lbestPSO［9-10］被用来优化参数C、ε。粒子i 的位置向量和速度向量分别定义为xi=［xi1，xi2］和vi=［vi1，vi2］，其第一维和第二维分别对应于参数C 和ε。同时，粒子的位置和速度更新公式如下:

图1 参数C、ε 对SVR 模型精度的影响Fig.1 Influence of the parameters ε and C on the accuracy of SVR model

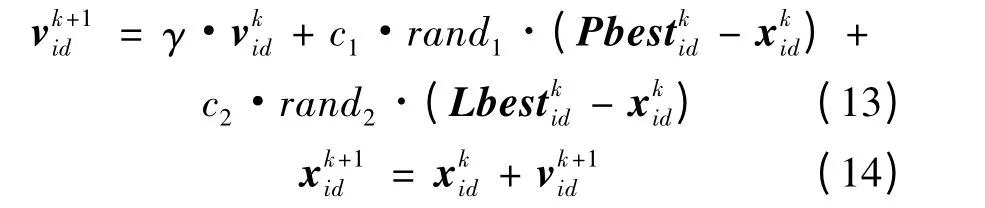
式中:γ 为惯性因子;c1、c2为学习因子;rand1、rand2为0 到1 之间服从均匀分布的随机数;为粒子i 第k 次迭代后的最优位置;为粒子i 第k 次迭代后在其邻域中的最优位置。另外，粒子的全局最优位置由Gbestk表示。

2.3.2 lbestPSO 算法改进

为了抑制粒子早熟，本文引入变异操作:若粒子i 的位置向量xi与目前发现的全局最优位置Gbestk的空间距离小于给定的最小距离Dmin时，对该粒子进行如下变异操作［11］:

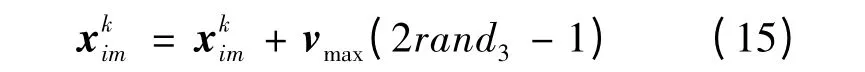
式中:rand3是0 到1 之间服从均匀分布的随机数。

同时为了提高算法的全局搜索能力，引入一种非线性自适应调节惯性因子［12］，如下式所示:

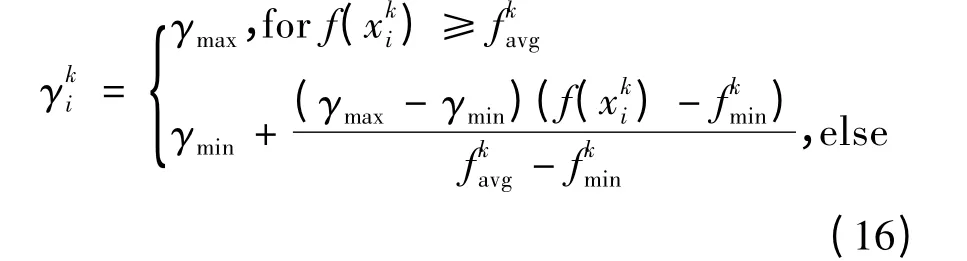
式中:f(·)为粒子的适应度函数;γmax和γmin分别为γ 的最大值和最小值;分别为第k 次迭代所有粒子的适应度函数的最小值和平均值。

上述改进后的算法在本文中称为Improved lbest PSO 算法。

2.3.3 基于Improved lbest PSO 的SVR 模型参数选择

利用参数(C，ε)，本文将Improved lbest PSO算法和SVR 模型耦合，耦合后的模型简称为Improved lbest PSO-SVR 模型。同时为了得到最优的C、ε，本文将模型的均方根误差作为Improved lbest PSO 算法的目标函数(即粒子的适应度函数)，其定义如下:

式中:r 为样本的数量;di为y 的实际值;fi为SVR模型对y 的估计值;RMSE 为均方根误差。其中di和fi的表达式为:

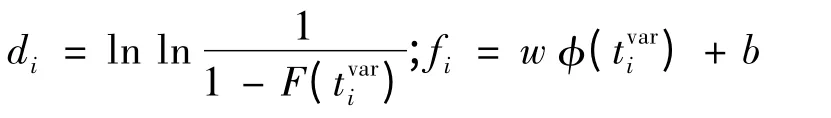
支持向量回归模型的参数可通过求解下面的优化问题得出:

参数C、ε 的具体优化过程如下所示。

Step1 参考表1，初始化Improved lbest PSO算法中的参数;

Step2 随机产生N1个粒子的位置和速度向量;

Step3 将每个粒子用于支持向量模型学习，确定每个粒子相应的(w，b);

Step4 利用式(17)计算每个粒子的适应度;

Step6 利用式(16)计算粒子群中每个粒子的自适应调节惯性因子γ;

Step7 利用式(13)更新粒子群中每个粒子的速度向量，并将粒子的速度限制在规定的速度范围内;

Step8 利用式(14)更新粒子群中每个粒子的位置向量，并将粒子的位置限制在规定的位置范围内;

Step9 判断各粒子是否满足变异条件:如满足则按照上述变异方式对该粒子进行变异处理;

Step10 判断是否满足结束条件:若满足则停止优化过程，否则返回Step3。

3 数值仿真

假设加工中心的故障密度函数为:

首先，本文根据上述故障密度函数产生数量为20、30、50 的故障间隔时间样本集。为了能够对支持向量回归模型的参数进行优化，本文将样本集(含l 个元素)分为两类，分别是训练组、校验组［13］。校验组样本(含r 个元素)用于估计参数C、ε，训练组样本(含l－r 个元素)用于估计可靠性模型的参数，其中校验组的样本数常为总样本数的1/4。为了使Improved lbest PSO 算法能够更高效地工作，其所需参数初始值设置如下:c1=c2=1.4962;wmax=0.9;wmin=0.4;Cmax=300;Cmin=1×10－5;εmax=0.5;εmin=1×10－5;Dmin=1;N1=40;迭代次数为300;误差为1×10－5。

粒子群多样性定义如下式所示，用以衡量改进前、后算法的性能。

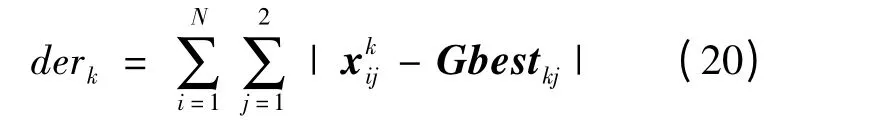
式中:N 为粒子数量。

为了比较Improved lbest PSO-SVR、LSM、MLE、局部最优粒子群优化算法优化的支持向量回归模型(lbest PSO-SVR)和遗传算法优化的支持向量回归模型(GA-SVR)的性能，MTBF 估计值的相对误差被作为各方法的综合评价指标，其计算公式如下:

式中:MTBF 通过式(4)计算。当计算MTBFreal时，f(t)为实际故障密度函数(见式(19));当计算MTBFest时，f(t)为估计得到的故障密度函数。

在上述基础上，本文用LS、MLE、lbest PSOSVR、Improved lbest PSO-SVR 和GA-SVR 对上述加工中心可靠性进行估计。不同样本下，Improved lbest PSO、lbest PSO 和遗传算法对参数C、ε 的优化结果如表1 所示。从表1 可知，Improved lbest PSO 的均方根误差小于lbest PSO和遗传算法。

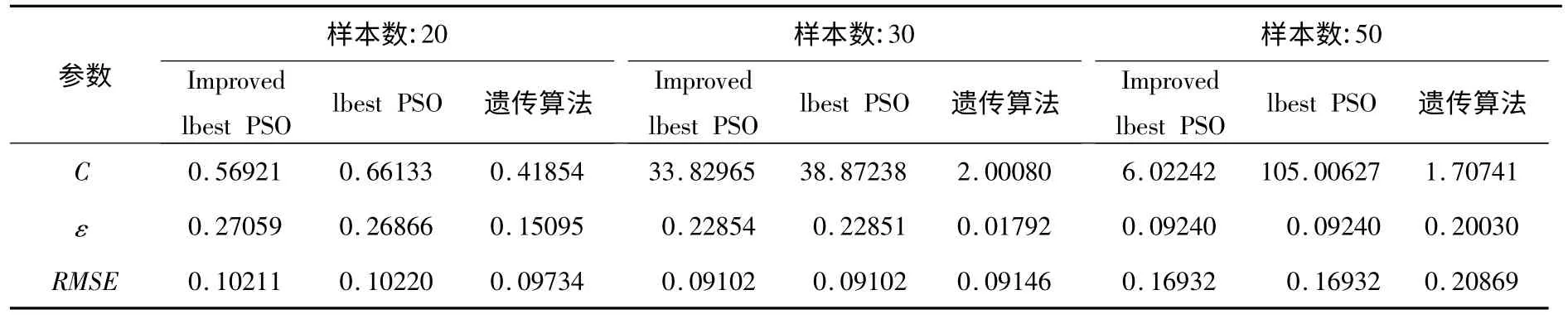
表1 参数C、ε 的优化结果Table 1 Optimization results of the parameters C and ε

图2 为适应度函数和粒子群多样性的变化情况。从图2(a)可知，Improved lbest PSO 算法的收敛速度比lbest PSO 算法更快;从图2(b)可知，Improved lbest PSO 算法保持着较高的多样性，而lbest PSO 算法的多样性则逐渐下降为0，这表明Improved lbest PSO 算法得到的参数更可信。上述现象证明了本文引入的变异操作、自适应惯性因子使得Improved lbest PSO 算法的性能优于lbest PSO 和遗传算法。

表2 为LSM、MLE、lbest PSO-SVR、GA-SVR和Improved lbest PSO-SVR 对上述加工中心故障密度函数的参数估计结果。各方法估计误差都在10%以下，但Improved lbest PSO-SVR 模型的相对误差小于5%，并且小于其他方法的估计误差。

图2 改进前、后lbest PSO 算法的性能对比Fig.2 Performances comparison between the lbest PSO algorithm and improved lbest PSO algorithm

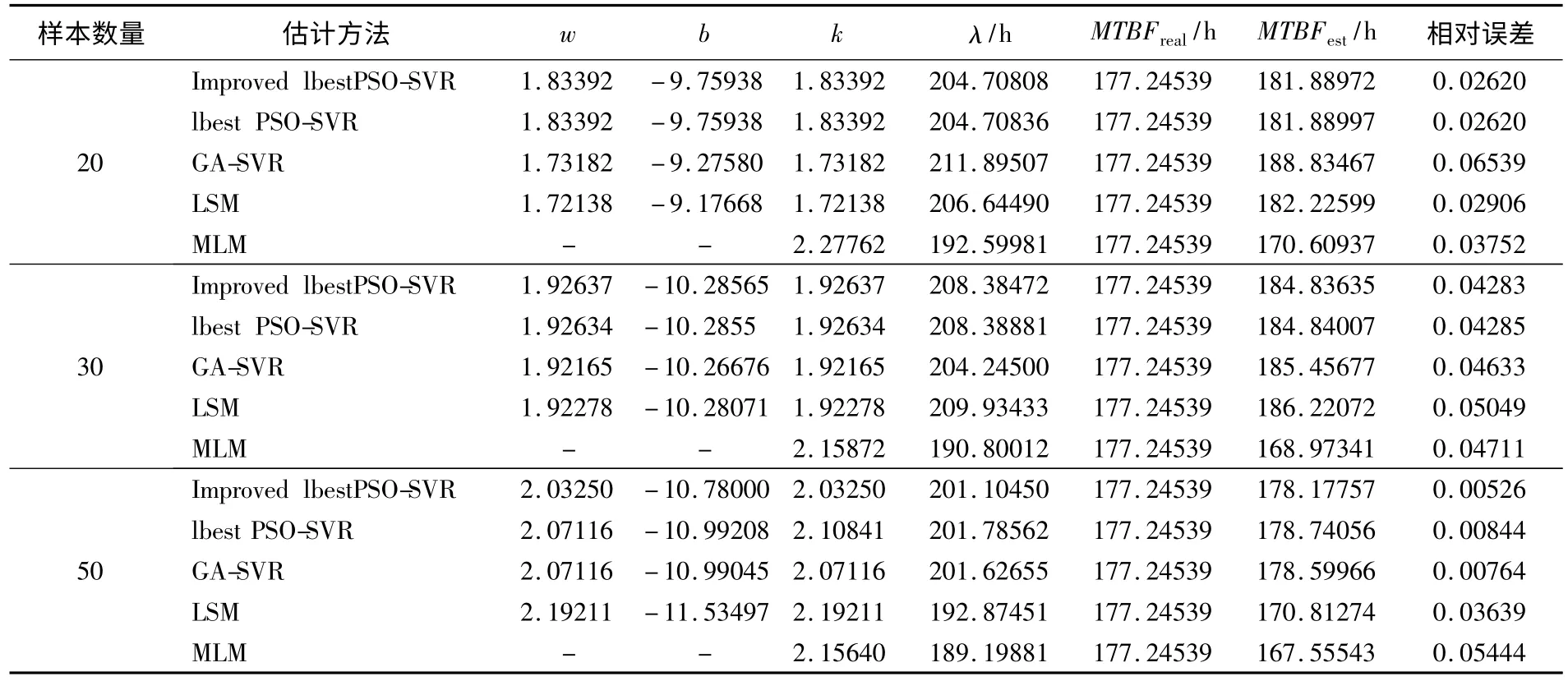
表2 LSM、MLE、SVR 的估计结果Table 2 Estimation results of LSM，MLE，SVR

图3(a)、图4(a)、图5(a)分别表示l=20，l=30 和l=50 时，Improved lbest PSO-SVR 模型的估计结果，其中，最佳SVR 模型所需的支持向量机数量分别是13、4、12，并且得到的回归直线与数据拟合良好。图3(b)、图4(b)、图5(b)表示LSM、MLE、Improved lbest PSO-SVR 得到的故障时间间隔分布函数。从图中可知，上述各方法都能较好地估计故障分布函数的参数，但是Improved lbest PSO-SVR 估计的故障分布函数与真实的故障分布函数最接近。因此，Improved lbest PSO-SVR 性能优于LSM、MLE、lbest PSOSVR、GA-SVR。

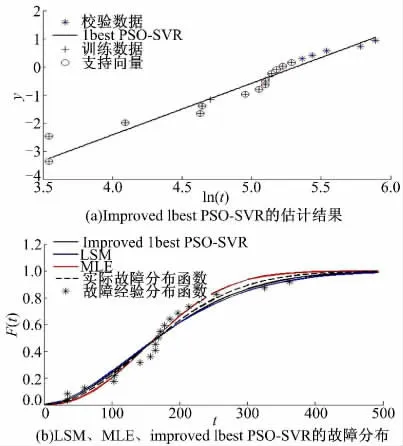
图3 样本数量l=20 时，各方法的估计结果Fig.3 In the l=20 case，estimation results of every method

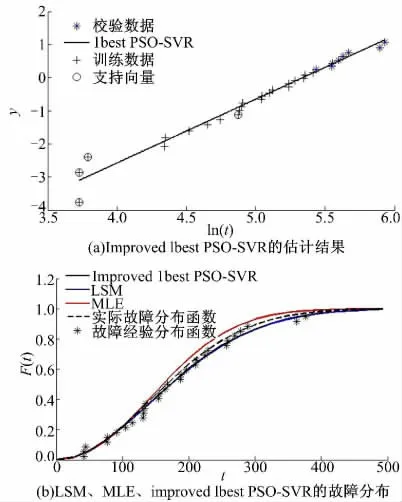
图4 样本数量l=30 时，各方法的估计结果Fig.4 In the l=30 case，the estimation results of every method

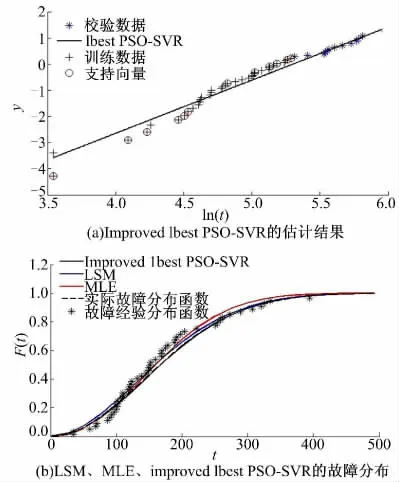
图5 样本数量l=50 时，各方法的估计结果Fig.5 In the l=50 case，the estimation results of every methods

4 应 用

某系列加工中心的44 条故障间隔时间数据如图6(a)所示。根据3.2 节的线性化处理方式，故障间隔时间数据的线性处理结果如图6(b)所示。从图6(b)可知，线性处理后的数据基本在一条直线上，因此可判断该系列加工中心的故障间隔时间服从威布尔分布。

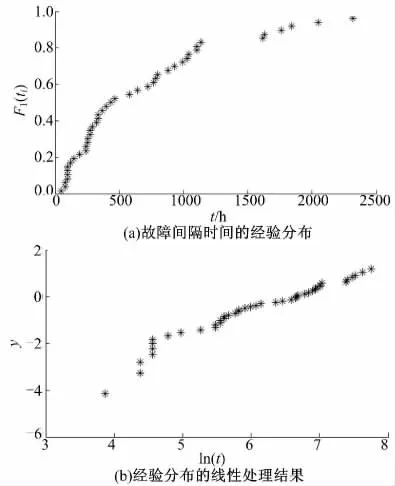
图6 某加工中心的故障间隔时间Fig.6 Fault time intervals of a actual machining center

采用Improved lbest PSO-SVR 模型对该加工中心的可靠性模型进行参数估计，其中Improved lbest PSO 算法的参数设置参见第3 节。此外，将故障间隔时间分为两组:训练组(含33 个元素)和校验组(含11 个元素)。Improved lbest PSOSVR 模型的估计结果如下:w =0.988;C =0.186;b=－6.521;ε=0.064;k=0.988;MTBF/h=735.693;λ/h=734.288。

图7 为利用Improved lbest PSO-SVR 模型估计得到的回归直线。从图7 可知，最佳SVR 模型所需的支持向量机数量为24，同时SVR 模型能自动地剔除故障样本中的异常样本。由Improved lbest PSO-SVR 得到的该加工中心的故障分布函数和可靠度函数的估计结果如图8 所示。同时利用Improved lbest PSO-SVR 模型估计出的参数值可以确定该加工中心的故障密度函数。利用式(5)可得，该机床的MTBF 估计值为735.693 h。这一估计结果将为该加工中心的可靠性增长提供基础依据。

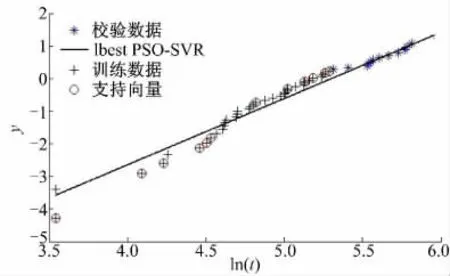
图7 Improved lbest PSO-SVR 估计结果Fig.7 Estimation results of improved lbest PSO-SVR

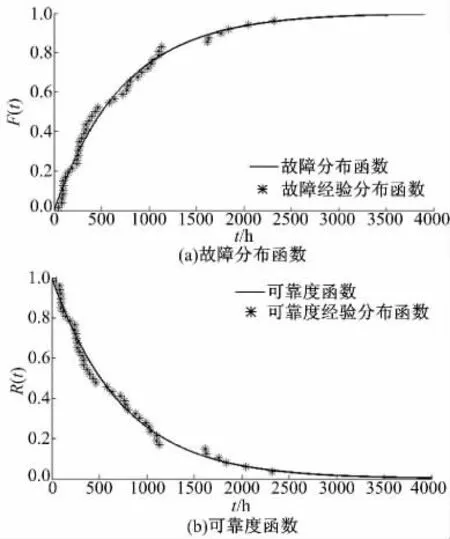
图8 某加工中心的可靠性估计结果Fig.8 Reliability assessment results of a actual machining center

5 结 论

(1)提出了改进的粒子群优化支持向量回归模型，并将其应用于可靠性领域，成功地对加工中心可靠性模型的参数进行了估计，其估计精度优于最小二乘法、最大似然估计法、原局部最优粒子群优化算法和遗传算法优化的支持向量回归模型，由此建立的加工中心可靠性模型具有较高的可靠性评估精度。

(2)引入的变异操作、自适应调整惯性因子提高了改进的局部最优粒子群优化算法的全局寻优能力和收敛速度，使其优于原局部最优粒子群优化算法和遗传算法。同时改进的局部最优粒子群优化算法优化后的支持向量回归模型具有较高的参数估计精度。

［1］杨兆军，陈传海，陈菲，等.数控机床可靠性技术的研究进展［J］.机械工程学报，2013，49(20):130-139.Yang Zhao-jun，Chen Chuan-hai，Chen Fei，et al.Progress in the research of reliability technology of machine tools［J］.Journal of Mechanical Engineering，2013，49(20):130-139.

［2］Balakrishnan N，Kateri M.On the maximum likelihood estimation of parameters of Weibull distribution based on complete and censored data［J］.Statistics＆Probability Letters，2008，78(17):2971-2975.

［3］Wu H C.Fuzzy reliability estimation using Bayesian approach［J］.Computers ＆ Industrial Engineering，2004，46(3):467-493.

［4］Vapnik V.Statistical Learning Theory［M］.New York:Wiley，1998.

［5］杨兆军，李小兵，许彬彬，等.加工中心时间动态可靠性建模［J］.机械工程学报，2012，48(2):16-22.Yang Zhao-jun，Li Xiao-bing，Xu Bin-bin，et al.Time dynamic reliability modelling of machining center［J］.Chinese Journal of Mechanical Engineering，2012，48(2):16-22.

［6］Bryan D.The Weibull Analysis Handbook［M］.ASQ Quality Press，2006.

［7］Smola Alex J，Bernhard S.A tutorial on support vector regression［J］.Statistics and Computing，2004，14(3):199-222.

［8］吴坚，赵阳，何睿.基于支持向量机回归算法的电子机械制动传感器系统故障诊断［J］.吉林大学学报:工学版，2013，43(5):1178-1183.Wu Jian，Zhao Yang，He Rui.Fault detection and diagnosis of EMB sensor system based on SVR［J］.Journal of Jilin University(Engineering and Technology Edition)，2013，43(5):1178-1183.

［9］Kennedy J，Mendes R.Population structure and particle swarm performance［C］∥Proceedings of the 2002 Congress on Evolutionary Computation，Honolulu HI，USA，2002:1671-1676.

［10］寇晓丽，刘三阳.基于模拟退火的粒子群算法求解约束优化问题［J］.吉林大学学报:工学版，2007，37(1):136-140.Kou Xiao-li，Liu San-yang.Particle swarm algorithm based on simulated annealing to solve constrained optimization［J］.Journal of Jilin University(Engineering and Technology Edition)，2007，37(1):136-140.

［11］王凌，刘波.微粒群优化与调度算法［M］.北京:清华大学出版社，2008.

［12］Engelbrecht A P.Fundamentals of Computational Swarm Intelligence［M］.Hoboken:John Wiley ＆Sons，2006.

［13］Lins I D，Moura M C，Zio E，et al.A particle swarm‐optimized support vector machine for reliability prediction［J］.Quality and Reliability Engineering International，2012，28(2):141-158.