基于出行时间可靠性的支路网络均衡分析

徐光明，王英姿，2，史 峰，秦 进

(1.中南大学 交通运输工程学院，长沙410075;2.湖南大学 土木工程学院，长沙410082)

0 引 言

城市交通网络用户均衡分析方法［1-2］和长期习惯性用户均衡分析方法［3-4］在城市交通组织中具有重要意义。用户均衡分析使得路径出行时间达到用户均衡;长期习惯性用户均衡分析在给定出行时间可靠的基础上使得路径出行时间达到用户均衡。由于支路路段较窄，可靠性较差，人们通常更愿意选择干道出行，所以，对支路网络而言，长期习惯性用户均衡分析具有特殊意义。

通行能力降级程度是道路网络的属性之一。相比于支路路段，更小的通行能力降级程度通常会导致干道路段平均饱和度更大一些。为了描述网络通行能力的不确定性，反映因自然灾害、恶劣天气、交通事故、道路维护等造成的随机通行能力降级，提出了出行时间可靠性的概念。Sumalee等［5］针对通行能力降级路网在一定可靠度下研究了用户均衡模型。Lo 等［3-4］通过构建长期习惯性均衡模型，针对多类风险意识群体，研究了通行能力降级路网中的出行时间预算问题，从降级网络和可靠性的角度深化了均衡分析的研究内容。

支路网络的均衡分析与一般意义的城市交通网络均衡分析存在较大差异，这是因为在一些支路路段上双向车流不分道行驶，虽然能够双向调剂使用路段通行能力，但路段通行能力与双向流量比例相关，越对称的双向流量的路段通行能力越小。Wang 等［6］利用元胞自动机模型模拟分析了双向支路路段的通行能力，获得其在不同方向流量比例分布下的路段通行能力、车辆平均速度与路段宽度之间的关系曲线，以及在不同方向流量比例分布下主路和辅路饱和流量、车辆平均速度与路段宽度之间的关系曲线。史峰等［7］进一步提出了双向支路路段通行能力依赖于路段宽度、单车道通行能力、双向流量比例等因素的近似解析公式，扩展了双向支路路段费用的解析表达式。

本文注意到支路网络中随机通行能力降级现象比干道网络更为严重的规律性，结合出行时间的可靠性研究了支路网络均衡问题。通过分析双向支路路段通行能力特征，结合扩展的支路路段的出行时间函数，针对各类路段通行能力降级特征，分别描述各类路段能力降级参数，在长期习惯性均衡模型基础上，构建了基于出行时间可靠性的城市支路网络均衡分析模型。设计了逐个起点分步实施的相继平均法，通过将交通分配的常规相继平均法进行分拆，求解该模型，并进行了相应的算例分析。

1 考虑支路双向干扰和出行时间可靠性的支路网络均衡问题

在城市道路网络N=(V，A ∪B1∪B2)中，V 为节点集，V={v1，v2，…，vn};A 为干道路段集;B1为单行道支路路段集;B2为不分道行驶支路路段集。

当路段a ∈A ∪B1∪B2时，C－a 为路段a 的通行能力上限;θa∈(0，1)为路段通行能力降级参数;路段a 的实际通行能力Ca为随机变量，在区间中服从均匀分布。显然，降级参数θa越大，能力降级程度越小。一般来说，干道路段的通行能力降级参数最大，单向支路路段次之，双向支路路段最小。

当a ∈A ∪B1时，为常数;当a ∈B2时，根据文献［7］，为双向支路路段a 与反向路段的共同通行能力，可用如下公式表示:

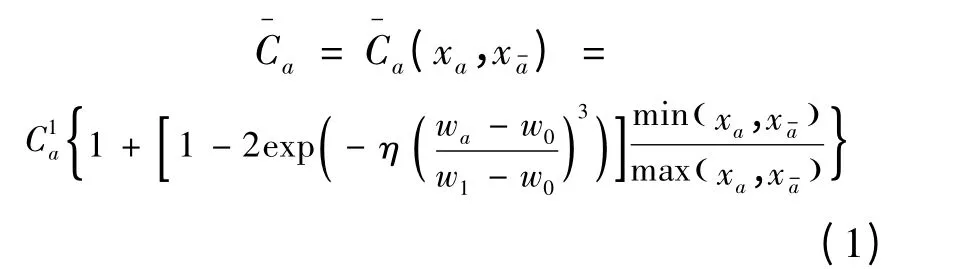
当a ∈A ∪B1时，出行时间采用标准BPR 函数:

式中:ta0为路段a 的自由流出行时间;α 和β 为参数，显然Ta也是随机变量。

当a ∈B2时，出行时间采用BPR 函数的拓展形式:

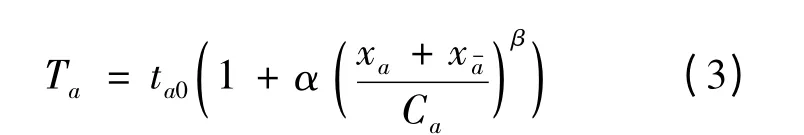
RS ⊂V×V 为O-D 需求点对集，qrs，(r，s)∈RS 为O-D 需求。

基于出行时间可靠性的支路网络均衡分析问题面向支路网络，考虑路网随机通行能力降级和支路双向干扰，在保证可靠度ρ 的情况下，以路径出行时间预算作为路径费用，对已知交通需求进行用户均衡交通分配。

2 基于出行时间可靠性的支路网络均衡模型

记Krs为O-D 对(r，s)之间的路径集，fp为路径p ∈Krs上的流量。从双向支路路段通行能力方面扩展Lo 等［3-4］的思想，假设不同路段通行能力相互独立，则路段费用的期望和方差分别为:

由中心极限定理，路径p 的出行时间Tp=近似地服从正态分布，数学期望E(Tp)和方差σ(Tp)2分别为:

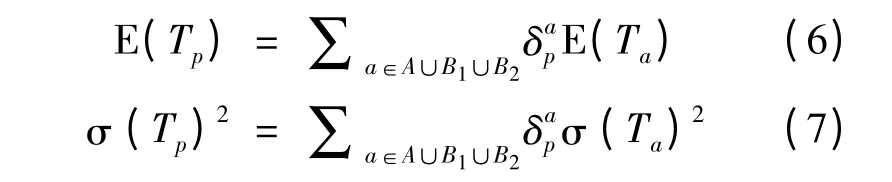
出行者在路径p ∈Krs上基于可靠度ρ 的出行时间预算为:

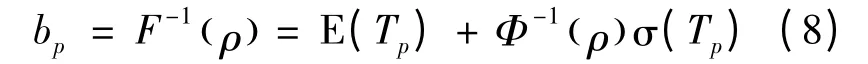
在降级路网中，用户以出行时间预算最短为准则选择路径，由Wardrop 第一原理，在支路网络中任意点对之间最小出行时间预算πrs与路径出行时间预算bp、路径流量fp之间满足如下关系:

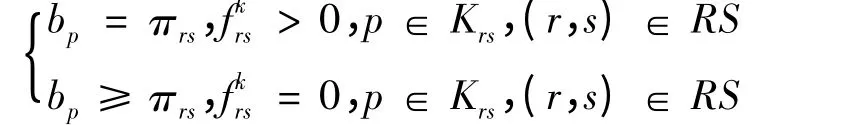
因此，基于出行时间可靠性的支路网络用户均衡问题可通过以下不等式组求解:

式(4)～式(15)等价于数学规划模型:

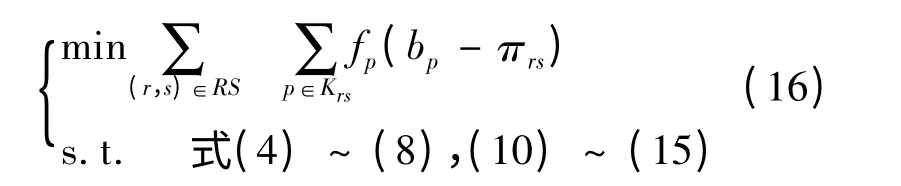
由于数学规划模型的目标函数非负，所以当且仅当最优目标函数值为零时达到用户均衡。

3 本文算法

基于出行时间可靠性的支路网络用户均衡数学规划模型与常规基于出行时间可靠性的用户均衡模型的差异，在于双向支路路段费用的数学期望E(Tp)和方差σ(Tp)的表达式不同，由于路径费用的不可加性，所以采用路径配流方法和相继平均法设计模型的求解算法。

由于双向支路路段的通行能力与双向流量比例有关，使得基于出行时间可靠性的城市支路网络均衡分析的数学规划模型不是凸规划，如果对所有O-D 流的全有全无分配同时实施相继平均处理，则可能导致支路路段双向流量比例大幅振荡，通行能力也相应地大幅振荡，难以保证算法的收敛性。为了解决这个问题，对常规的相继平均法进行分解，逐个起点相继平均处理，这样可以明显降低双向流量比例的振荡幅度，达到提高收敛速度的目的。

路径配流的适用性及相关问题已被广泛讨论［8-12］。由于路径费用的不可加性，难以在全体路径集内求解，为此，先求取没有重复点的k-最短路径集，再在该路径集中求解出行时间预算最短路径。综上所述，设计求解算法如下。

算法1 基于出行时间可靠性的支路网络用户均衡交通分配算法

输入:支路网络N=(V，A ∪B1∪B2);单向支路路段通行能力参数;双向支路路段通行能力参数和η，w0，w1，wa;θa，a ∈A ∪B1∪B2;O-D 需求qrs，(r，s)∈RS;可靠度ρ;k-最短路集参数k;收敛参数ε。

输出:流量xa，a ∈A ∪B1∪B2;流量fp，p ∈Krs，(r，s)∈RS 和时间预算πrs，(r，s)∈RS。

4 算例分析

含支路路段的网络如图1 所示，由17 个节点构成，所有双实线为干道路段(除了路段(3，11)、(11，7)、(7，1)的通行能力上限为2400 pcu/h 以外，其他干道路段的通行能力上限均为1600 pcu/h)，所有单实线段为支路路段(路段宽度均为4.85 m)，具有箭头的支路路段为单行道，其箭头指向为单向行驶方向，其他支路路段为双向不分道行驶，干道路段双向分道行驶，图中数字表示各路段的自由流时间，单位为min(干道路段双向具有等值能力和自由流出行时间，图中仅列出单方向数据)。交通需求量如表1 所示。支路路段的单向单车道通行能力均为C1a=800 pcu/h。

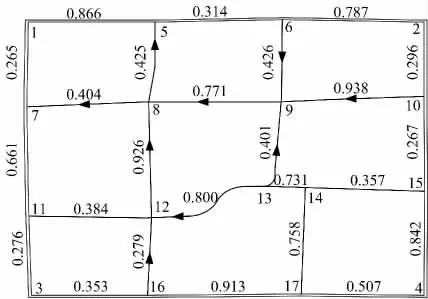
图1 算例网络Fig.1 Test network

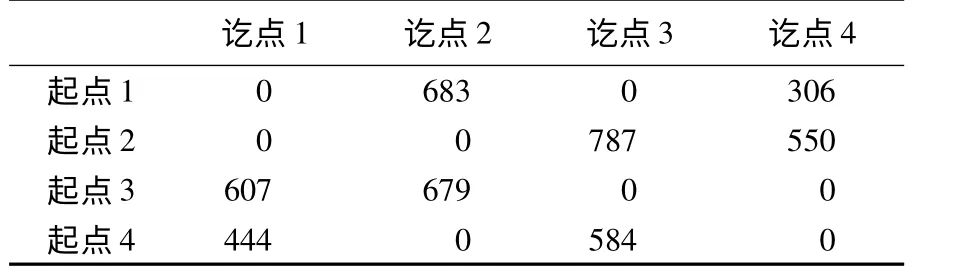
表1 交通需求(pcu/h)Table 1 Traffic demands(pcu/h)

无论是干道路段还是支路路段，均取α =0.15，β=4，可靠度ρ=0.9，路段降级参数为:

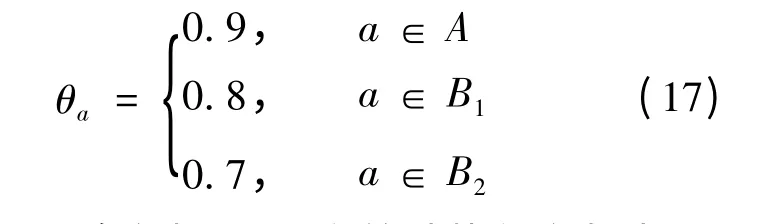
以上是网络参数设置，在算法执行参数中，设置k-最短路集参数k=5，收敛参数ε=10－5。考虑多种交通需求水平，以表1 交通需求为基础，分别按照η 的倍数确定需求。利用算法1 分别求解各种需求进行交通分配，其路段分类平均饱和度的变化趋势如图2 所示。

从图2 可以看出:路段平均饱和度都随着需求水平的增加而单调增加，干道平均饱和度几乎与需求水平等比例增加，支路平均饱和度随需求水平的增长速度相对平缓。

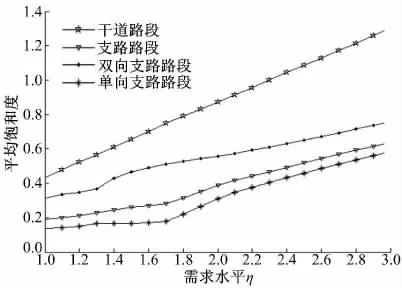
图2 路段平均饱和度与需求水平η 的关系曲线Fig.2 Relation curves between the average saturation of road sections and the demand level η

总体来看，干道平均饱和度高于支路平均饱和度、双向支路路段平均饱和度高于单向支路路段平均饱和度。产生这种现象的原因有两个:其一为网络结构所致(一些支路不便于利用)，其二为支路路段能力降级程度更大。

图3 展示了网络中各双向路段流量、通行能力关于需求水平的变化趋势，图中的正向表示标明弧段的相同方向，反向则是与之相反的方向，比如在路段(11，12)的子图中，正向为点11 至点12的方向，反向为点12 至点11 的方向。

由文献［4］可知，对于这些宽度仅为4.85 m的路段，双向行驶通行能力低于单向行驶通行能力，并且随着双向流量的对称性增加通行能力进一步减小。路段(11，12)和(14，15)的双向流量都较大，组织双向行车是合理的，除了较低的需求水平外，双向流量趋于对称，通行能力趋于下降，并且在需求水平η=3 时都已处于饱和状态。至于路段(13，14)和(14，17)，除了较低需求水平外都是单向流量，这两个路段的饱和度都较低。

最后，再分析一下不同可靠度对出行者选择干道和支路出行的影响。在可靠度ρ =0.9 和ρ=0.2 两种情形下，干道和支路路段平均饱和度与需求水平的关系曲线如图4 所示。显然，在任何一个需求水平上，可靠度ρ=0.9 对应的干道平均饱和度较大，支路的平均饱和度较小，平均饱和度的这种大小关系随着需求的增加几乎等比例增加。当可靠度ρ=0.2 时，与可靠度ρ=0.9相比，支路平均饱和度增加，干道平均饱和度减少。相比之下，干道平均饱和度的差异性没有支路的显著，其原因在于干道路段通行能力远高于支路路段通行能力。由此看来，在较高可靠度的期望下，出行者更倾向于选择干道而不选择支路出行;或者说，越保守的出行者选择支路出行的概率越小。

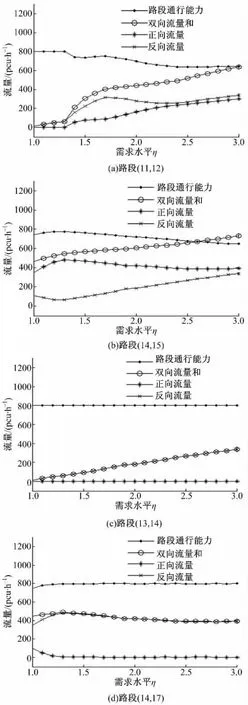
图3 双向支路路段通行能力、双向流量和、正反方向流量与需求水平的关系曲线Fig.3 Relation curves between the demand level η and the capacity，total two-way flows，traffic flows with two different directions in two-way branch road sections

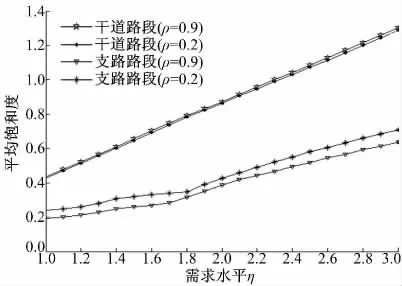
图4 不同可靠度下路段平均饱和度与需求水平η 的关系曲线Fig.4 Relation curves between the average saturations of road sections under different travel time reliabilities and the demand level η

5 结 论

(1)在随机通行能力降级的城市支路网络中，由于双向路段通行能力与双向流量比例相关，可以在长期习惯性均衡模型基础上，增加双向路段通行能力特征，构建基于出行时间可靠性的城市支路网络均衡分析模型。

(2)由于双向路段的通行能力特征，使得基于出行时间可靠性的城市支路网络均衡分析的数学规划模型不是凸规划，为了提高收敛性，可逐个起点分步实施相继平均法，以降低每一步的波动，提高算法收敛性。

(3)由于干道通行能力降级程度较支路更小，在同等可靠度条件下，干道路段平均饱和度比支路更大。在支路网络交通组织优化中，只要合理描述路段能力降级参数，便可获得合理的饱和度状态，更真实地反映了支路网络出行的可靠性特征。

(4)在不同的可靠度要求下，出行者对干道和支路选择结果是有差异的。在较高可靠度的期望下，出行者更倾向于选择干道、而不选择支路出行;或者说，越保守的出行者选择支路出行的概率越小。

［1］Sheffi Y.Urban Transportation Network:Equilibrium Analysis with Mathematical Programming Methods［M］.New York:Prentice Hall，1985.

［2］黄海军.城市交通网络平衡分析-理论与实践［M］.北京:人民交通出版社，1994.

［3］Lo H K，Tung Y K.Network with degradable links:capacity analysis and design［J］.Transportation Research Part B，2003，37(4):345-363.

［4］Lo H K，Luo X W，Siu B.Degradable transport network:Travel time budget of travelers with heterogeneous risk aversion［J］.Transportation Research Part B，2006，40(9):792-806.

［5］Sumalee A，Watling D P.Travel time reliability in a network with dependent link modes and partial driver response［J］.Journal of the Eastern Asia Society for Transportation Studies，2003，5:1686-1701.

［6］Wang Ying-zi，Long Dong-fang，Shi Feng.Cellular automation model for analyzing the capacity of branch road section［J］.Journal Central South University of Technology，2011，18(5):1744-1749.

［7］史峰，王英姿，徐光明，等.考虑支路路段双向车流相互影响的交通网络均衡分析［J］.中国公路学报，2013，26(3):137-142.Shi Feng，Wang Ying-zi，Xu Guang-ming，et al.Traffic flow equilibrium analysis of urban road traffic system with bi-directional flow＇s effect of local road［J］.China Journal of Highway and Transport，2013，26(3):137-142.

［8］Lo H K，Chen A.Traffic equilibrium problem with route-specific costs:formulation and algorithms［J］.Transportation Research Part B，2000，34(6):493-513.

［9］Chen A，Lo H K，Yang H.A self-adaptive projection and contraction algorithm for the traffic assignment problem with path-specific costs［J］.European Journal of Operational Research，2001，135(1):27-41.

［10］Han D，Lo H K.Solving non-additive traffic assignment problems:a descent method for co-coercive variational inequalities［J］.European Journal of Operational Research，2004，159(3):529-544.

［11］Xu M，Chen A，Qu Y，et al.semismooth newton method for traffic equilibrium problem with a general nonadditive route cost［J］.Applied Mathematical Modelling，2011，35(6):3048-3062.

［12］Chen A，Zhou Z，Xu X.A self-adaptive gradient projection algorithm for the nonadditive traffic equilibrium problem［J］.Computer＆Operations Research，2012，39(2):127-138.