多车道环形交叉口车头时距分布模型

曲昭伟，段宇洲，宋现敏，陶鹏飞，邢 岩

(吉林大学 交通学院，长春130022)

0 引 言

环形交叉口作为一种特殊的交通控制设施，在通行能力、延误以及安全性等方面都有着独特的优势。车头时距作为联系微观交通和宏观交通的桥梁，不仅是微观仿真模型的基本输入参数，同时也是预测通行能力的基础，直接影响着交通系统模型的精确程度。Ha 等［1］将车头时距的概率分布模型精确地划分为单一模型、组合模型和混合模型3 类。目前存在的两种混合模型为Buckley 提出的半泊松分布和Cowan 和Branston所提出的GQM 模型［2-3］。针对双车道公路，基于对车辆行驶状态的分类，常玉林等［4］提出了改进的M3 分布模型。Zhang 等［5］提出了一种新的参数估计方法，采用GQM 模型和DDNED 模型对高速公路数据进行拟合检验。臧晓冬等［6］利用绝对值韦布尔模型对城市快速路合流区的车头时距进行了建模。Al-Ghamdi［7］通过划分流量界限，在快速路和城市干线车头时距分析中证明了爱尔朗分布的优良拟合性。陶鹏飞等［8］针对快速路路段的车头时距构建了包含负指数分布和正态分布的混合模型。韩萍［9］初步建立了环形交叉口的车头时距混合模型。He 等［10］建立了移位负指数分布乘以高斯分布的综合概率分布模型，使车头时距和速度从宏观上得到结合。Mauro 等［11］从统计意义上阐释了移位对数正态分布，并结合实际交通问题验证了其实用性。刘明君［12］通过对信号交叉口处排队消散进行研究，提出了基于风险分析的释放车头时距模型。

综上，目前所研究的大都是针对高速公路、城市快速路及一般路段的车头时距的结果，而对于环形交叉口车头时距的研究成果相对较少。且由于单车道环岛车辆运行情况相对简单，而多车道情况下由于车道之间的差异性对整个环岛的影响更为突出，所以对多车道环岛的车头时距研究更加迫切。

本文针对不同类型环岛的不同区域和不同车道，利用多种分布模型对车头时距进行拟合，并利用最大似然法和Levenberg-Marquardt 法来估计参数，采用单样本Kolmogorov-Smirnov(KS)检验来比较各个模型之间的优劣。并通过双样本KS 检验对不同组合的车头时距分布情况进行了探讨，为环形交叉口系统的基本特性研究提供了参考。

1 数据采集及预处理

选取长春市赛德广场和新民广场作为调查对象，其中，赛德广场为无信号控制，新民广场为单停车线信号控制。两者均为多车道大型环岛，环岛平均直径大于150 m。采用录像调查方式，选取调查地点周边高层进行俯拍，并采用视频处理软件Corel VideoStudio 对车头时距进行人工提取，精度可达0.04 s。按照车流的运行方式，将环形交叉口的区域划分为环流区和交织区。其中环流区车辆行为相对简单，主要为环道内车辆的绕环行为，而交织区中的车辆行为相对复杂，大量的车辆交织行为对通行能力产生了较大影响。如图1 所示，断面A 所处的位置为环流区，断面B 所处的位置为交织区。为了叙述方便，将最内侧车道定义为车道1，相邻车道为车道2，以此类推。选取赛德广场仙台大街南段至南湖大路东段、新民广场工农大路北段至延安大街段作为研究路段，在正常气候和交通条件下进行数据采集，对主要数据进行统计分析，如表1 所示。

图1 区域划分示意图Fig.1 Diagram of area dipartition

由表1 可以看出，两种控制方式下，在环流区，平均车头时距从内车道向外车道有递增趋势;对于交织区，由于新民广场的车流量较大，三条车道的平均车头时距相差较小，最大相差为15.96%;但在赛德广场，由于无信号控制，车辆为了避免在外侧车道中受进口车辆的干扰便倾向于在内侧车道行驶，平均车头时距也呈由内到外递增的趋势。为了更加直观地分析两个环岛的车头时距情况，绘制出箱线图，如图2 所示。

图2 中，按照箱线图所计算的可信度区间，原样本数据中有异常值存在。赛德广场中从交织车道到环流车道，车头时距分布呈逐渐扩大趋势，而新民广场各个车道的分布形式则较为集中，同标准差的结果一致。

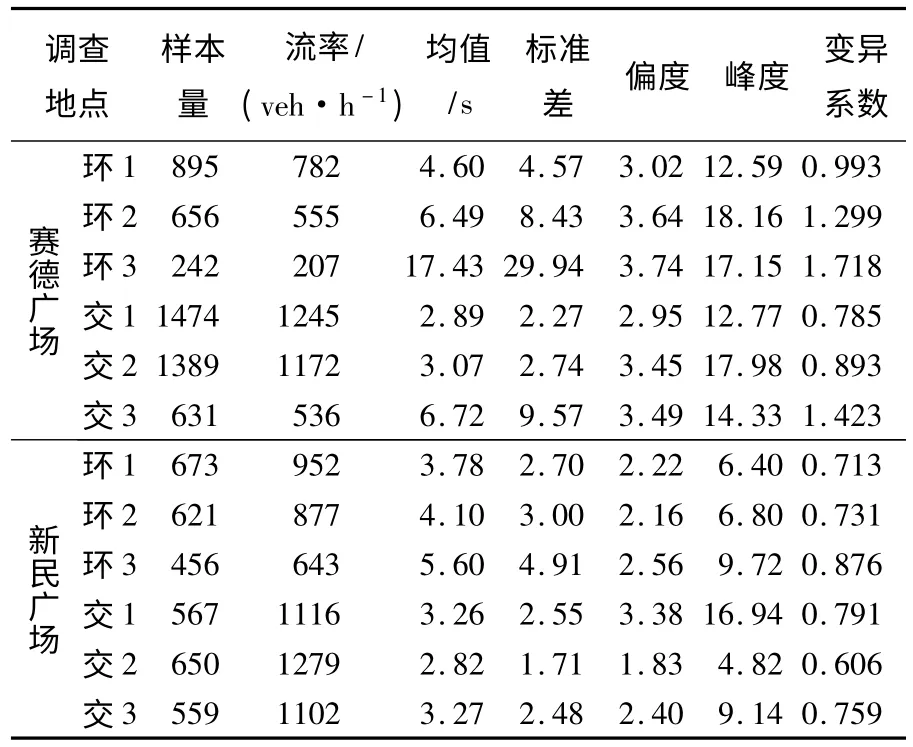
表1 不同区域车道的车头时距描述统计特性Table 1 Statistic description of headway of different lanes

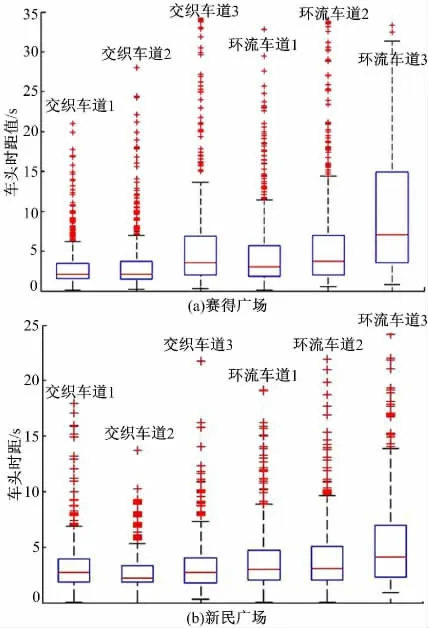
图2 各车道车头时距箱线图Fig.2 Boxplot of different headways

为了精确地得到各个车道的车头时距分布情况，以实际调查数据为样本绘制出累计概率分布图，如图3 所示。从图3 中可以看出:对于不同的控制方式，其分布形式差异较大;相对而言，信号控制方式所得到的车头时距分布情况更为集中，而无信号控制方式由于车流在入口处呈随机到达，所以车流的分布较为分散。此外，还可以看出，车道由内到外，出现大时距的可能性逐渐增加。

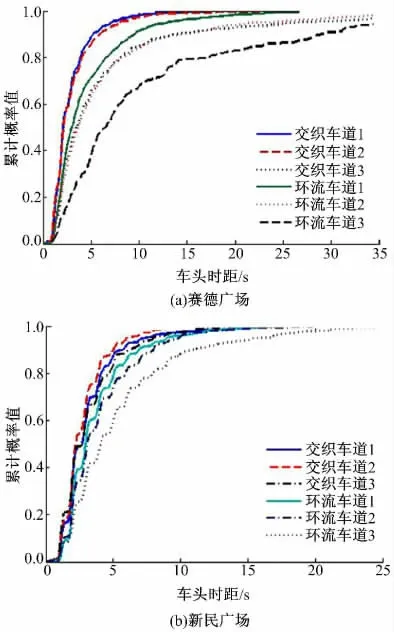
图3 调查地点样本累计概率分布图Fig.3 Cumulative probability distribution of the survey sample

2 分布模型及参数估计

对公路交通的车头时距描述中，经常采用韦布尔分布、对数正态分布等基本形式，部分学者也指出用Cowan M3 模型来拟合环岛车道的车头时距分布较为合适［13］。为了更加精确地描述车头时距，Wasielewski 提出Buckley 所建立的半泊松分布将更加适合描述车头时距［14-15］。而Branston［3］根 据 排 队 系 统 提 出 了GQM 模 型，Cowan［2］也提出了适合一般情况的M4 分布模型，Zhang 等［5］对这两种分布模型进行了简单的推导，结果表明两者实际上为同一形式的不同表达。但如式(1)(2)所示，不论是半泊松分布模型还是GQM 模型，由于其本身函数定义的复杂性和待定参数较多，在实际应用过程中受到限制，如半泊松分布模型需对跟驰车头时距进行拉普拉斯变换，所以本文只对Cowan M3 分布进行研究，其基本形式如式(3)所示。

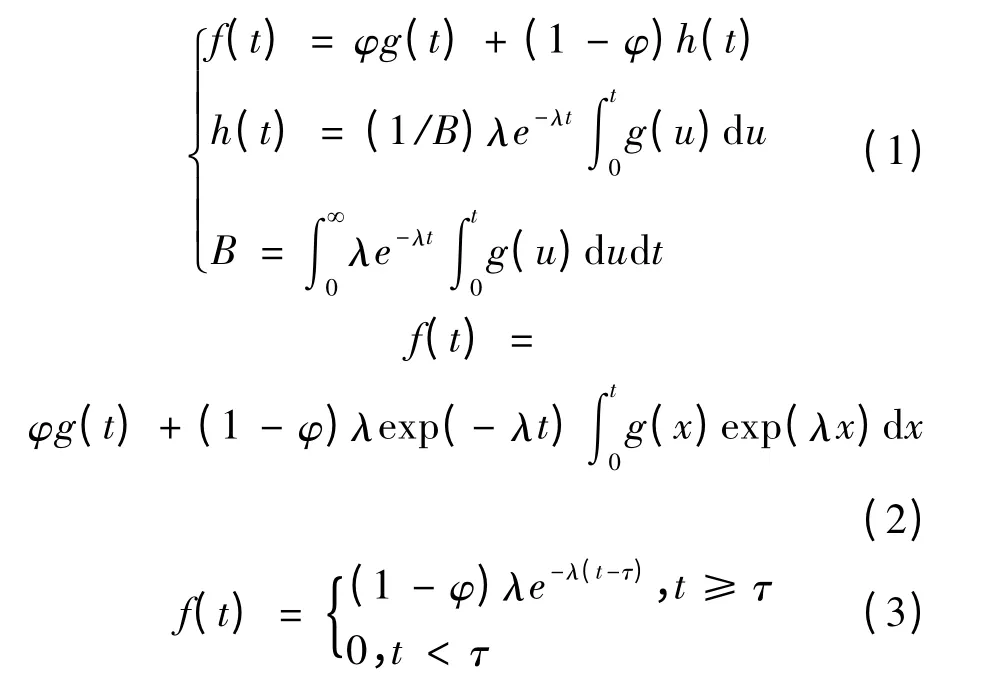
式中:f(t)为概率密度函数;φ 为跟驰流比例;g(t)为跟驰车流的概率密度函数;h(t)为自由流概率密度函数;λ 为衰减常量;τ 为最小车头时距。

Jang 用JohnsonSB 模型对郊区干线的车头时距分布进行了拟合［16-17］，由于此模型中带有两个形状参数，能根据实际情况而做出灵活调整，其基本模型如式(4)所示:

式中:z=(x－ξ)/λ;x 为车头时距变量，范围值为［ξ，ξ+λ］;γ 为形状参数;δ 为另一形状参数，δ ＞0;λ 为尺度参数，λ ＞0;ξ 为位置参数。

广义极值分布(Generalized extreme value distribution)的概率密度函数如式(5)所示:

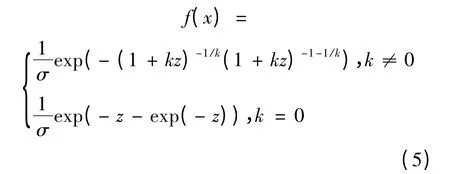
式中:z ≡(x－μ)/σ，σ 为尺度参数，且σ ＞0;μ为位置参数;k 为形状参数。

Griffiths 和Hunt［18］提出了双移位负指数模型(DDNED)，其概率密度函数如式(6)所示:

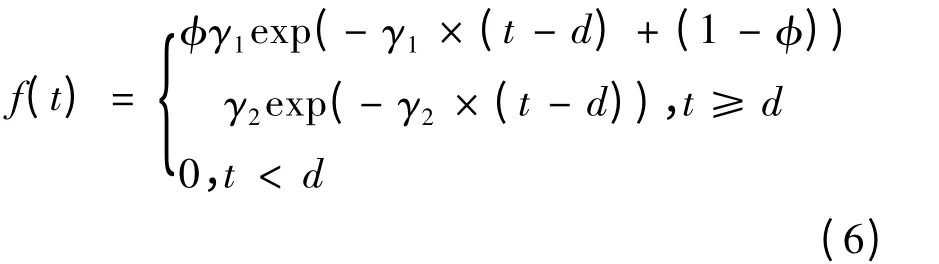
式中:φ 为权重系数，0 ＜φ ≤1;γ1和γ2为流量影响系数;d 为移位参数。

最大似然估计方法(MLE)对参数预测效果较为显著，本文采用MLE 和Levenberg-Marquardt法［19-20］对3 种模型的参数进行了非线性回归分析预测，参数估计值如表2 所示。其中，α、β、γ 分别代表形状参数、尺度参数和位置参数。

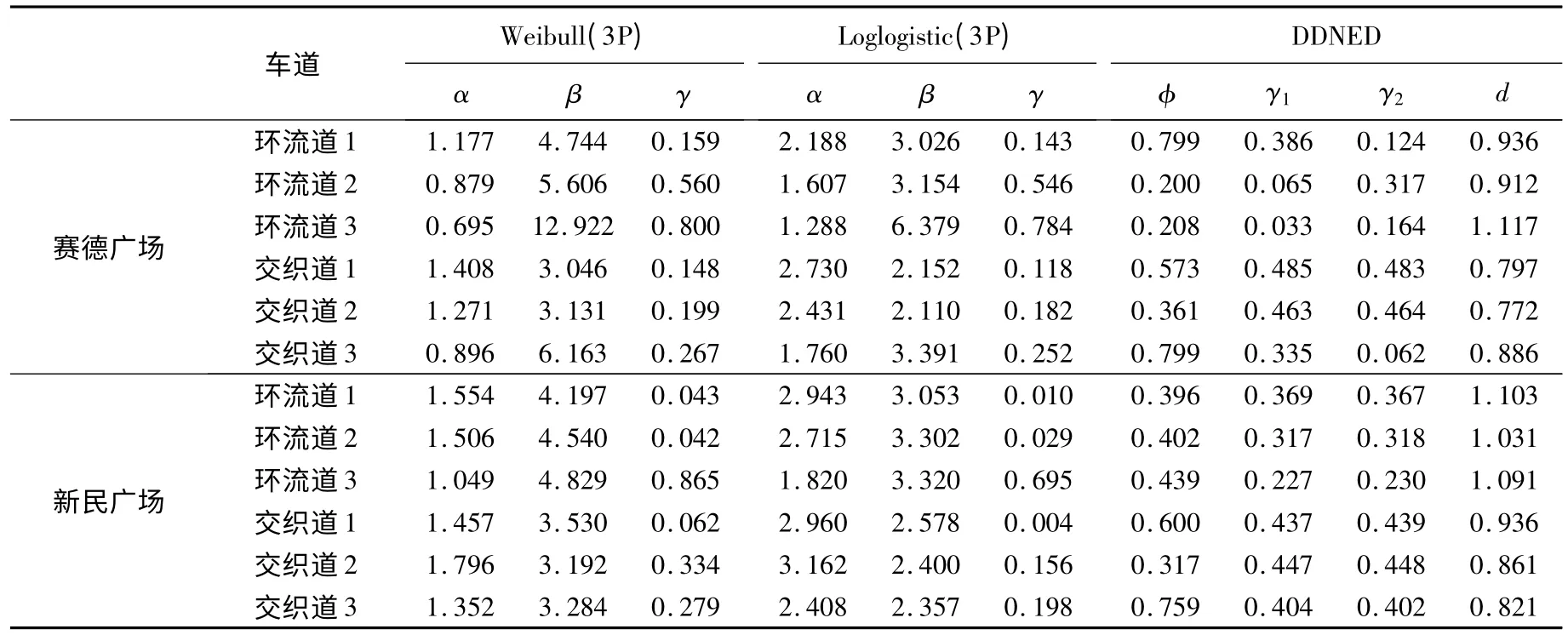
表2 模型参数估计值Table 2 Estimated values of model parameters

3 分布拟合比较和检验

选取赛德广场和新民广场的不同区域位置的车头时距数据作为样本集，利用上述方法对车头时距分布模型进行拟合。为了对分布模型的拟合性能进行定量比较，选用单样本KS 检验对拟合效果进行定量测试，其中选用0.05 对应的显著性水平的临界值进行检验，检验结果如表3 所示。为了更形象地表现分布特性，选取概率密度函数图和P-P 图进行表达。其中，P-P 图表示经验分布累计概率和理论模型累计概率之间的关系，点集越趋于线性表明其理论分布函数越接近真实分布。在模型参数标定的基础上，选取几条典型车道进行拟合对比分析。

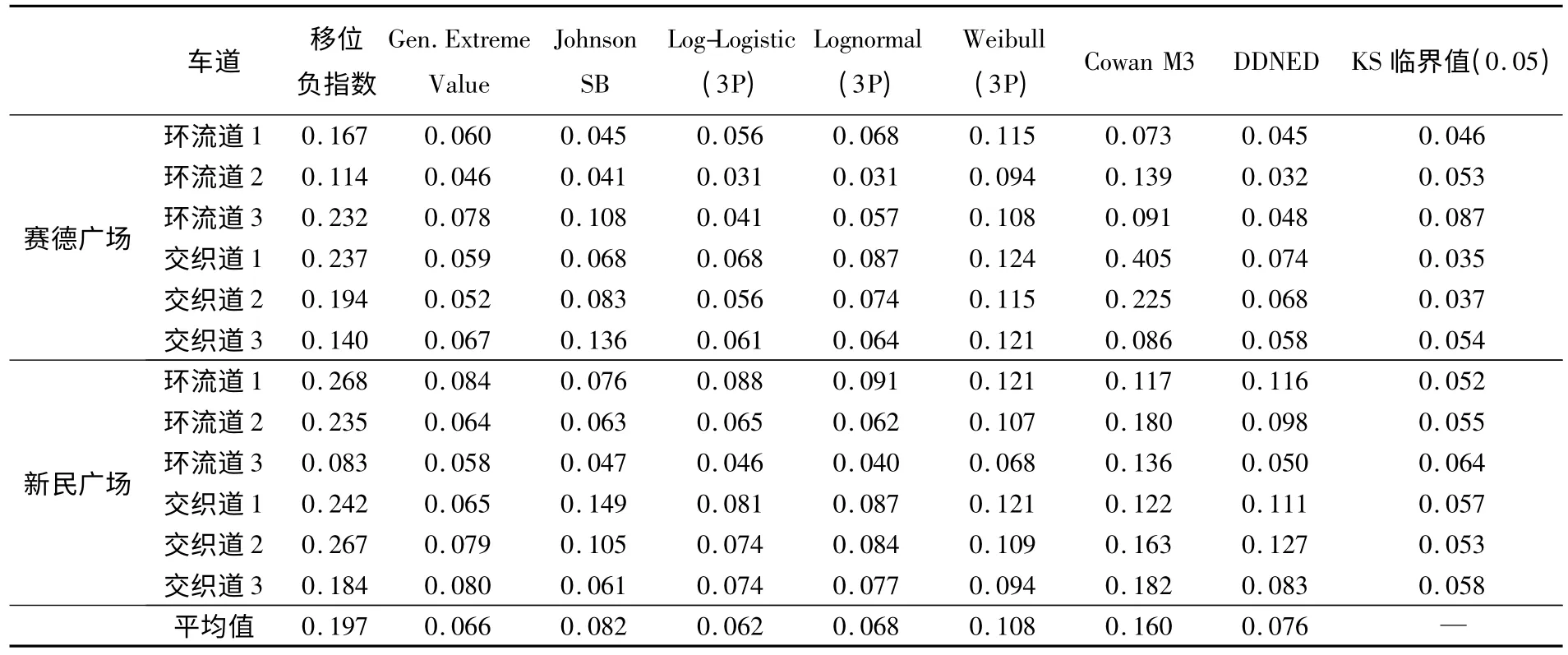
表3 各种模型的拟合优度K-S 检验值Table 3 Goodness of fit test for various models

首先选取赛德广场的环流车道2 进行分析，结合图4(a)(b)和表3 中的数据，移位负指数分布、Cowan M3 分布和Weibull 分布拟合效果较差，而其他几种分布模型的拟合效果较好，最大KS 检验值为0.46，小于检验临界值，图4(b)的P-P 图也呈现出这种趋势。图4(c)(d)为赛德广场的交织车道2 的概率分布拟合图，其中移位负指数的拟合效果较差，结合KS 检验值，极值分布模型中的检验值为0.052，而Cowan M3 的检验值为0.225，差距较大，从侧面也体现了分布模型对结果影响的重要性。从图4 可以看出，P-P 图反映出几种分布模型对环流车道2 的拟合效果要优于对交织车道2 的拟合效果，表3 的KS 检验结果中也证实了这种趋势。

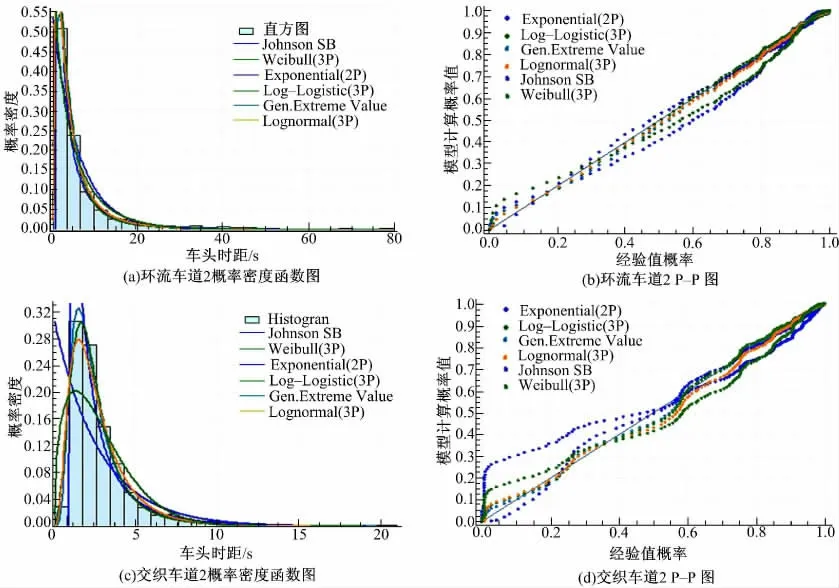
图4 赛德广场环流车道2 和交织车道2 的概率分析图Fig.4 Probability distribution of circulating lane 2 and weaving lane 2 at Saide square

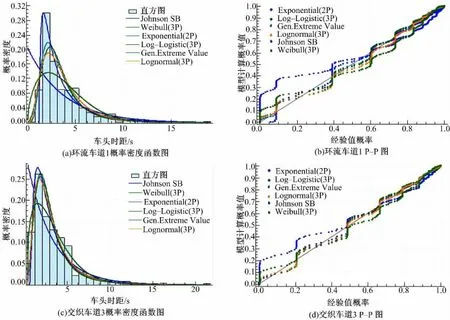
图5 新民广场环流车道1 和交织车道3 的概率分析图Fig.5 Probability distribution of circulating lane 1 and weaving lane 3 at Xinmin square

图5 为新民广场的环流车道1 和交织车道3的概率分析图。对于环流车道1，用Johnson SB模型所得到的KS 检验值最小，为0.076;而交织车道3 中，用Johnson SB 模型同样达到的最优的拟合效果，KS 检验值最小。但可能是受到参数估计方法的精度影响，所得到的结果并未通过KS检验。结合P-P 图分析可知，当车头时距较小时，理论累计分布概率均小于经验累计分布概率值，此时拟合的效果稍差，但是这种差异的波动性会随着车头时距的增大而逐渐减小。

采用类似方法对其他车道的车头时距分布情况进行分析，分析结果如表3 所示。从平均水平上分析，移位负指数效果最差，KS 检验平均值为0.197，而移位对数logistic 分布效果最好，KS 检验平均值为0.062。从各个车道的角度进行分析，Gen.Extreme Value 分布、Johnson SB 分布、移位Log-Logistic 分布、移位 Lognormal 分布和DDNED 分布的表现性能较好;而移位负指数分布、Cowan M3 分布和Weibull 分布的检验效果稍差，对应于不同车道处的KS 临界值，其都未能通过检验。相比而言，由于环流区车流运行形式较为简单，车辆换道等行为相对较少，所以用本文的几种分布模型对其拟合的效果相对较好。而由于交织区的车辆受到其他车辆汇入或驶出的影响，车头时距的分布情况较为复杂，传统的分布模型如移位负指数分布等拟合效果较差，无法满足拟合精度要求;对于混合分布的拟合，由于参数估计方法本身的不足，虽然拟合精度较传统分布模型已有很大提高，但部分结果还是未能通过检验，需对模型参数进一步标定。

综上，对于不同的控制类型以及不同的区域条件，上述模型中均有能够合理表达车头时距分布状况的模型，但不同条件下各个模型具有适应性差异。例如，对于赛德广场的环流区，DDNED分布均能达到一个较好的效果，最大KS 检验值小于0.048，而移位对数正态分布和移位对数logistic 分布在环流道2 和环流道3 的拟合效果较好;对于赛德广场的交织区，广义极值分布和DDNED 的检验效果优于其他分布形式。对于新民广场，受信号控制的影响其车流的到达形式也发生了变化，对于环流区，Johnson SB 模型和移位对数正态分布模型的拟合效果较好;而对于交织区的不同车道，其拟合形式变化较大，对于交织车道1、2、3，其最优拟合分布模型分别为广义极值分布、移位对数logistic 分布和Johnson SB 分布。所以，在实际应用中应根据不同的条件选用合适的分布模型，并且进行精确的参数标定，为交通系统的运行提供准确的参考。

4 车道间分布模型相关性检验

以上分析均是将不同的分布模型应用于不同车道，独立进行分析的。为从整体上把握环形交叉口的车头时距分布情况，假设各个车道之间独立分布，对两两车道间的分布情况进行分析，采用双样本KS 检验法对各个车道之间的分布相关性进行检验。用矩阵来表示各车道间的相关性，其中，矩阵的行分别为［{环流车道1}，{环流车道2}，{环流车道3}，{交织车道1}，{交织车道2}，{交织车道3}］，列为行的转置项。原假设H0为两个样本总体分布相同，用F1(X)和F2(X)表示两个样本的累计经验分布函数，则KS 统计量为，临界值的计算如式(7)所示:

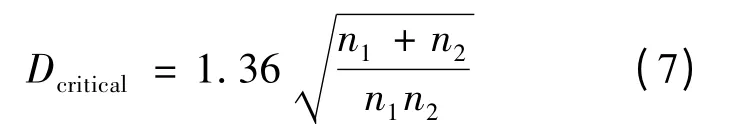
式中:n1、n2为样本量。

以新民广场为例，判断矩阵用A表示，临界矩阵用B 表示，检验矩阵用C 表示。若A［i，j］＜B［i，j］，则C［i，j］=1，接受原假设，否则拒绝原假设。检验矩阵结果如C 所示，其中矩阵元素1 表示两者分布相同，0 表示两者分布不同。

由矩阵C 可以看出，对于新民广场，环流车道1 和环流车道2 之间的分布类型近似相同。交织车道1 和交织车道2，交织车道1 和交织车道3之间的分布也近似相同。类似地可得到赛德广场的判断矩阵、临界矩阵以及检验矩阵分别如矩阵D、E、F 所示。从结果可以看出，赛德广场只有交织车道1 和交织车道2 之间的分布类似，其他车道的车头时距的分布都为不同形式。

为了对同区域同车道在不同控制类型下的分布特性进行分析，采用同样的方法，对新民广场和赛德广场的环流车道和交织车道进行双样本KS检验，结果如表4 所示。经计算得到的KS 统计值均大于临界值，所以拒绝原假设，即分布形式不相同。可见受信号控制的影响，车流在环形交叉口内运行的形式发生了变化，车头时距分布形式亦发生了改变。

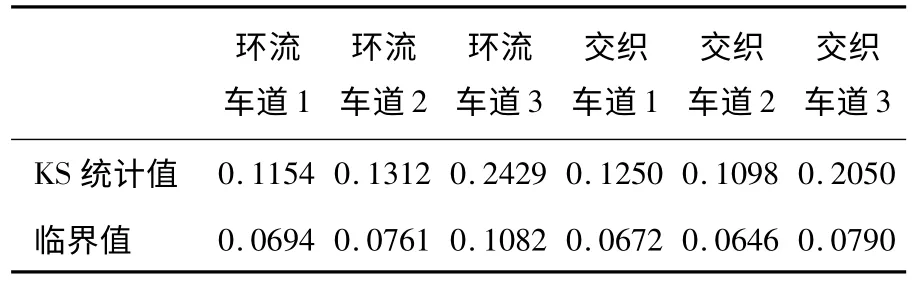
表4 赛德广场/新民广场同车道之间双侧KS 检验Table 4 Two sample KS test at Saide/Xinmin square

5 结束语

通过对不同控制类型的环形交叉口的不同区域的车头时距进行采集，结合最大似然估计方法和Levenberg-Marquardt 法等参数估计方法，采用8 种分布模型对其分布形式进行拟合，并通过KS检验对模型的拟合性能进行定量测试。此外，利用双样本KS 检验分析了车道间的相关性。结果表明，不同控制类型下的不同区域中的不同车道，其车头时距分布形式均有所不同，应选用不同的分布模型并对其进行精确标定。

［1］Ha D H，Aron M，Cohen S.Time headway variable and probabilistic modeling［J］.Transportation Research Part C:Emerging Technologies，2012，25:181-201.

［2］Cowan R J.Useful headway models［J］.Transportation Research，1975，9(6):371-375.

［3］Branston D.Models of single lane time headway distributions［J］.Transportation Science，1976，10(2):125-148.

［4］常玉林，王炜，邓卫，等.双车道公路车头时距分布模型研究及应用［J］.东南大学学报，1999，29(6):108-112.Chang Yu-lin，Wang Wei，Deng Wei，et al.Research of the headway distribution models on two-lane highways and their applications［J］.Journal of Southeast University，1999，29(6):108-112.

［5］Zhang Guo-hui，Wang Yin-hai，Wei Heng，et al.Examining headway distribution models with urban freeway loop event data［J］.Transportation Research Record，2007:141-149.

［6］臧晓冬，周伟.城市快速路互通立交合流区车头时距分布特性［J］.北京工业大学学报，2010，36(7):961-965.Zang Xiao-dong，Zhou Wei.Time headway distribution characteristics of merging area on urban expressway interchanges［J］.Journal of Beijiing University of Technology，2010，36(7):961-965.

［7］Al-Ghamdi A S.Analysis of time headways on urban roads:case study from Riyadh［J］.Journal of Transportation Engineering，2001，127(4):289-294.

［8］陶鹏飞，王殿海，金盛.车头时距混合分布模型［J］.西南交通大学学报，2011，46(4):633-638.Tao Peng-fei，Wang Dian-hai，Jin Sheng.Mixed distribution model of vehicle headway［J］.Jounal of Southwest Jiaotong University，2011，46(4):633-638.

［9］韩萍.环形交叉口交通流运行特性［D］.长春:吉林大学交通学院，2011.Han Ping.Traffic operation characteristics of roundabout［D］.Changchun:College of Transportation，Jilin University，2011.

［10］He Shu-yan，Guan Wei，Ma Ji-hui.Observed timeheadway distribution and its implication on traffic［C］∥Proceedings of the 12th International IEEE Conference on Intelligent Transportation Systems，St.Louis，USA，2009:803-808.

［11］Mauro R，Branco F.Some proposed models as regards vehicular time headway［C］∥Transportation Research Board，Washington DC，USA，2010:2-4.

［12］刘明君.基于混合交通流的信号交叉口机动车车头时距研究［D］.北京:北京交通大学交通运输学院，2010.Liu Ming-jun.Modeling on discharge headway with heterogeneous traffic at signalized intersections［D］.Beijing:School of Traffic and Transportation，Beijign Jiaotong University，2010.

［13］Hagring O.Estimation of parameters in distribution of headways in roundabouts［J］.Journal of Transportation Engineering，2002，128(5):403-411.

［14］Wasielewski P.An integral equation for the semi-Poisson headway distribution model［J］.Transportation Science，1974，8(3):237-247.

［15］Wasielewski P.Car-following headways on freeways interpreted by the semi-Poisson headway distribution model［J］.Transportation Science，1979，13(1):36-55.

［16］Jang Jinhwan，Park Changsoo，Kim Byunghwa，et al.Modeling of time headway distribution on suburban arterial:case study from South Korea［J］.Procedia-Social and Behavioral Sciences，2011，16:240-247.

［17］Jang J.Analysis of time headway distribution on suburban arterial［J］.KSCE Journal of Civil Engineering，2012，16(4):644-649.

［18］Griffiths J D，Hunt J G.Vehicle headways in urban areas［J］.Traffic Engineering＆Control，1991，32(10):458-462.

［19］姚荣涵，王殿海，李丽丽.机动车车头时距分布的韦布尔修正模型［J］.吉林大学学报:工学版，2009，39(2):331-335.Yao Rong-han，Wang Dian-hai，Li Li-li.Revised Weibull revision model of headway distribution for motor-vehicle［J］.Journal of Jilin University(Engineering and Technology Edition)，2009，39(2):331-335.

［20］Hung W T，Tian F，Tong H Y.Discharge headway at signalized intersections in Hong Kong［J］.Journal of Advanced Transportation，2003，37(1):105-117.