两难区引导系统激活时间的确定

贾洪飞，杨 东

(吉林大学 交通学院，长春130022)

0 引 言

黄灯启亮时陷入两难区的车辆既无法在停车线前安全停车也无法在红灯启亮前通过交叉口［1］。针对两难区问题，设计相应的规避系统十分必要，其中，绿灯延长系统(Green extension system，GES)是主要的规避系统之一［2］。GES 在高速车辆陷入两难区时延长绿灯，在达到最大绿灯延长时限或低速车辆陷入两难区之前结束绿灯，尽可能地降低车辆陷入两难区的风险。Yi［3］提出一种车辆跟踪的概念，通过车路通信技术确定最需要提供保护的区域，采用延长绿灯的措施规避车辆陷入两难区。Li 等［4］利用马尔科夫状态转移矩阵预测达到最大绿灯延长时限之前陷入两难区的车辆数，通过与当前陷入两难区的车辆数进行对比，决定是否延长绿灯。储浩等［5］基于智能车路系统，通过延长绿灯时间和信息提示的方法避免车辆陷入两难区。同时，研究人员对如何合理布设GES 系统也进行了深入研究［6］。然而，GES 系统依赖固定参数(如接近速度)进行布设，由于驾驶员或车辆具有不同的属性，导致车辆仍然存在陷入两难区的风险。

随着智能化交通工具的应用，实时、准确地获取各类交通信息已十分便利［7］。应用这些信息，可以构建两难区引导系统［8］，从而在黄灯启亮前确定车辆行驶行为，规避两难区。Moon［9］设计了一种车载两难区警示系统，通过在黄灯启亮前某一时刻激活车载设备，为驾驶员提供警示信息，辅助驾驶员决定是否通过交叉口。然而，预警系统的设计包括激活时间等仍然依赖固定的接近速度等参数。同时，基于警示信息的规避系统没有为驾驶员提供具体的驾驶策略，辅助作用有限。车载两难区规避系统尤其是系统激活时间(系统激活时距黄灯启亮剩余时间)的设定对于提升系统性能至关重要。鉴于此，本文在介绍一种基于提前引导的规避系统的基础上，通过分析系统激活时间对车辆引导的影响，提出了一种激活时间的确定方法，以便更科学、合理地布设引导系统。

1 基于提前引导的两难区规避系统

图1 为两难区引导系统流程;图2 为信号交叉口两难区示意图。图2 中，V 为接近速度;AB、BC 分别为某一车辆的两难区和可通行区长度;w为交叉口宽度;L 为车辆长度;γ 为全红时长。

如图1 所示，两难区引导系统流程包括5 个步骤［8］:①信息收集，黄灯启亮前利用车路协同技术获取车辆及时空状态信息，如车速、车辆与停车线之间的距离、黄灯启亮剩余时间、黄灯时长等，并且当前车存在时，前车的车辆状态信息及行驶行为也将被获取;②两难区状态分析，如图2 所示，两难区的存在将交叉口上游分为两难区、可通行区和可停车区3 个区域，在这一步骤，系统将分析黄灯启亮时车辆所处的区域;③确定行驶行为，当前车的行驶行为是通过交叉口时，车辆的行驶行为将通过两难区引导算法确定，引导算法根据获取的信息和车辆两难区状态，计算引导策略(加速策略—车辆加速至黄灯启亮后匀速通过交叉口;减速策略——车辆在恰当的时间减速停车;匀速策略——车辆保持当前的速度并匀速通过交叉口)，当前车减速停车时，车辆的行驶行为将通过警示信息确定，提醒驾驶员停车等待;④实现引导，对于通过引导策略确定的行驶行为，车辆将借助纵向控制系统实现车辆引导［10］，而对于通过警示信息确定的减速停车行为将由驾驶员自身完成;⑤信息发布，为了辅助后车确定行驶行为，利用无线通信方式，车辆通过广播等获取与行驶行为相关的信息。

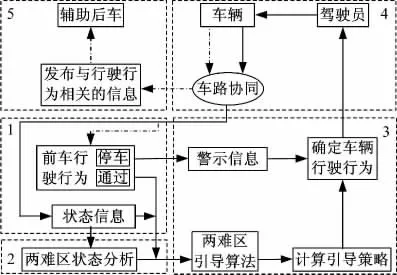
图1 两难区引导系统流程Fig.1 Flow of dilemma-zone avoidance-guiding system

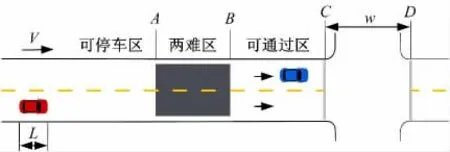
图2 信号交叉口两难区示意图Fig.2 Sketch map of dilemma zone at signalized intersection

不同于GES 系统，两难区引导系统在黄灯启亮前某一时刻被激活，引导车辆在规避两难区的前提下通过交叉口或安全停车。为避免较短或较长的激活时间给车辆引导带来的影响，需要设置合理的激活时间。本文根据车辆不同的接近速度，分两种情况分析了激活时间对车辆应用加速策略和减速策略的影响。

2 激活时间对车辆引导的影响

为了增加系统应用的广泛性，文中考虑了全红信号，即黄灯后增加一段全红时长γ，要求车辆在黄灯结束前通过停车线并在全红信号内通过交叉口［11］。这种情况下，接近速度不同，两难区边界的计算方式也不同。

(1)接近速度V ≥(w+L)/γ

这一情形下，黄灯结束时位于停车线的车辆可以在全红信号内通过交叉口，且两难区边界的计算公式为:

式中:V(τ)为黄灯启亮时的车速;dmax为车辆最大减速度;δ 为驾驶员反应时间(文中为纵向控制系统延迟1 s)。

在给定激活时间和相同车速的条件下，若使在黄灯启亮时位于两难区左边界(图2 中A 点)的车辆能够使用加速策略通过交叉口，则位于该两难区内其他位置的车辆也一定能够通过加速引导通过交叉口。因此，考虑黄灯启亮时位于两难区左边界的车辆应采用加速策略，使得加速后的车辆在黄灯启亮时到达可通行区，数学表达式为:

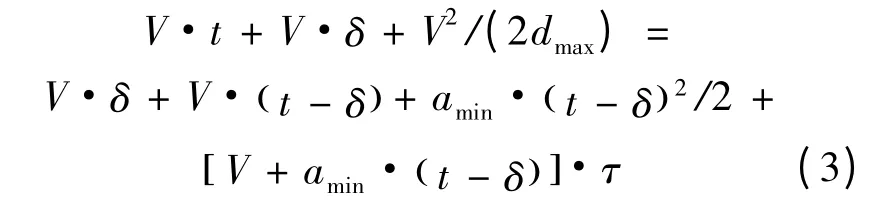
式中:t 为激活时间(黄灯信号启亮剩余时间);amin为车辆规避两难区所需的最小加速度。

为了保证驾驶舒适性，限定本文中的加速度不能超过舒适加速度acomfort(0.315 m/s2)［12］。由式(3)得:

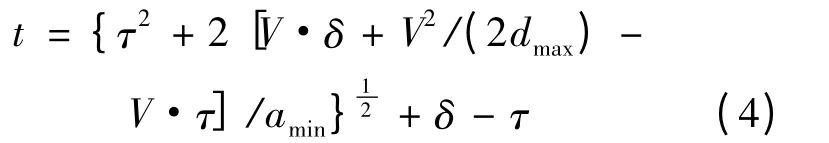
从式(4)中可以看出，当车速满足V ＞max{2dmax(τ－δ)，(w+L)/γ}时，激活时间t 关于车速V 是单调递增的。因此，对于将在黄灯启亮时位于两难区左边界，并且使用acomfort加速后车速小于路段限速Vlocal的车辆，激活时间设置得越长，可通过舒适加速度加速引导并到达可通行区的车辆的接近速度越大。文中通过给出实际算例说明这一结论，交叉口及车辆参数为:黄灯时长3 s、全红时长2 s、交叉口宽度30 m、车长6 m、限速27 m/s。激活时间为10 ～16 s 时，接近速度与最小加速度的关系如图3 所示。可见，激活时间越长，可引导的车辆的最大接近速度越大;当激活时间不超过14 s 时，随着激活时间的增大，可以使用舒适加速度acomfort实现加速引导的车辆的接近速度增大;然而，当激活时间超过14 s 时，虽然可引导的接近速度在增大，但由于使用acomfort加速后车速超过Vlocal，所以，此时加速引导车辆所使用的最小加速度小于acomfort。

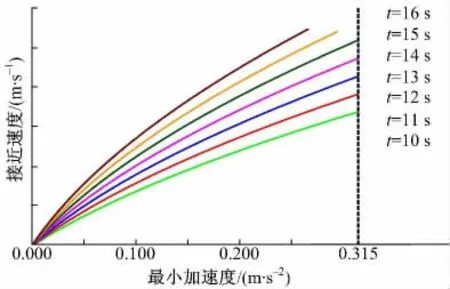
图3 不同激活时间对应的接近速度与最小加速度关系Fig.3 Relationship of approaching speed and minimum acceleration rate under different activation time

当接近速度V ≥(w+L)/γ 时，由于驾驶员舒适性和路段限速等因素的限制，并不是所有将要陷入两难区的车辆都存在一个有效的加速策略。当车辆不具备加速条件时，两难区引导算法将为车辆计算一个减速策略［8］。

考虑将在黄灯启亮时陷入两难区(图2 中AB)的车辆，立即执行减速策略的数学表达式为:

式中:S(τ)为系统分析车辆两难区状态时，t 秒后车辆与停车线之间的距离，且S(τ)＜AC;d 为减速策略中使用的减速度，考虑到驾驶员舒适性，文中d=0.5dmax。

由式(5)可知，当给定车速V 时，激活时间t越长，S(τ)的值越小。这说明，对于同一车速的车辆，只有设置足够长的激活时间，才可以保证原本在黄灯启亮时位于两难区右边界(图2 中B 点)的车辆，能够通过减速引导在停车线前安全停车。将位于B 点的车辆的S(τ)=BC 带入到式(5)，整理可得:

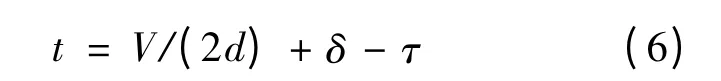
从式(6)可以看出:激活时间t 关于车速V 是单调递增的。因此，当接近速度V ≥(w+L)/γ时，激活时间设定的越长，可通过减速策略引导停车的车辆的接近速度越大。

(2)接近速度V ＜(w+L)/γ

这一情形下的车辆在全红信号内不可通过交叉口，且两难区边界的计算公式(2)转换为:

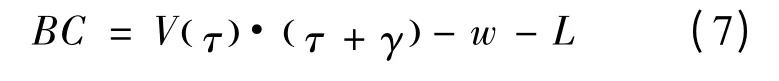
该情形下，原本在黄灯启亮时位于两难区左边界，且加速后能够通过交叉口的车辆应满足:

整理得:

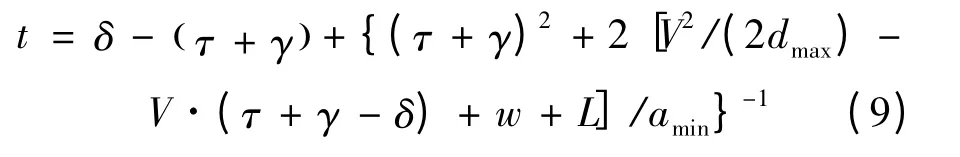
由于低速车辆完成加速后，车速不会超过路段限速，因此，只考虑车辆使用acomfort的情形。从式(9)可以看出:当V ＜min{(w+L)/γ，dmax(τ+γ－δ)}时，激活时间t 关于接近速度V 是单调递减的。因此，激活时间设定的越长，原本在黄灯启亮时位于两难区左边界、可以通过acomfort加速引导并在红灯启亮前通过交叉口的车辆的接近速度V 就越小。

考虑接近速度V ＜(w+L)/γ 时，激活时间对应用减速策略的影响。将式(7)带入式(5)，整理可得:

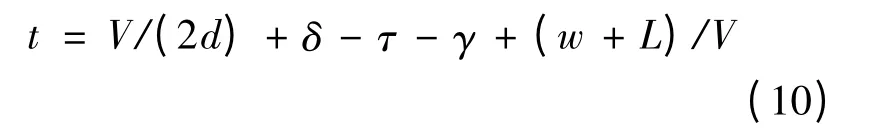
由式(10)可知，当接近速度V ＜(w+L)/γ且位于速度值较小的范围区间时，激活时间t 关于接近速度V 是单调递减的。因此，在这种情形下，激活时间设定的越长，可通过减速引导的车辆的接近速度越小。

综合以上分析，对于黄灯启亮时陷入两难区的车辆来说，激活时间越长，系统可加速或减速引导的车辆的速度范围越大，即处于不同速度区间(接近路段限速和低速)的车辆都可以通过加速策略或减速引导策略规避两难区。然而，设置较长的激活时间扩大了引导范围，因此，需要更多的路侧设备来实现引导系统，增加了系统布设成本。相反，设置较短的系统激活时间，又可能导致加速策略中的最小加速度超过acomfort而放弃加速，从而增加车辆停车等待产生的时间延迟。

3 激活时间的确定

根据激活时间对车辆引导影响的分析，在确定激活时间时，应充分考虑车辆应用加速策略和减速策略各自所需的激活时间，并选取其中的较大者作为最终的激活时间。

3.1 应用加速策略时所需激活时间的确定方法

存在全红信号时，对于将在黄灯启亮时位于两难区左边界的车辆，应用加速策略可能会面临下列3 种情形，激活时间应确定为max{ti}，i =1，2，3，其中，ti为每种情形对应的激活时间。

情形1 接近速度不小于(w+L)/γ

在这一情形下，车辆只需加速后在黄灯结束时到达停车线，即可保证在全红信号内通过交叉口，因此，应依据式(4)确定激活时间。由式(1)和式(2)得，当AB ＞0 时两难区存在，即:

车辆应用加速策略时确定的激活时间，至少应保证黄灯启亮时位于两难区左边界的车辆使用acomfort加速后速度不高于路段限速并通过交叉口，记求出的激活时间为ttemp，该激活时间对应的最大临界速度记为Vmax。结合对式(4)的分析，对于黄灯启亮时陷入两难区且V ＞d(τ－δ)的车辆，延长激活时间可以引导接近速度更大的车辆，并且能够保证最小加速度在舒适范围内，这里的d(τ－δ)为式(4)等号右边项根号内关于V 的函数取最小值时对应的车速。因此，在ttemp基础上，为确定该情形下需要的激活时间，文中给出了一种增益模型。

当系统激活时间为tα时，对于某一给定的车速为V(Vmax＜V ＜Vlocal)且可利用加速引导通过交叉口的车辆，在系统分析车辆两难区状态时，可知tα秒后该车速的车辆与停车线之间的最远距离为Sα;当系统激活时间延长至tβ时，系统分析两难区状态时，可知tβ秒后该车速的车辆与停车线之间的最远距离为Sβ，即激活时间的延长，使得系统在分析车辆两难区状态时，接近速度为V 且原本在黄灯信号启亮时位于Sα与Sβ之间的车辆，具备了加速条件。将系统激活时间延长带来的可引导范围的增加定义为系统增益，增益概率为P。黄灯信号启亮时车辆与停车线间的最远距离为:

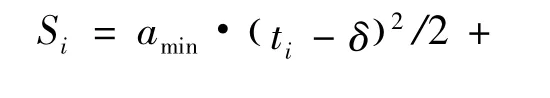
当V ＞Vmax时，若车辆加速后达到路段限速，则amin＜acomfort。因此，激活时间为tα时，amin=(Vlocal－V)/(tα－δ);激活时间为tβ时，amin=(Vlocal－V)/(tβ－δ);将amin代入式(12)后得到激活时间由tα延长至tβ时，对应的Sα和Sβ的计算公式为:

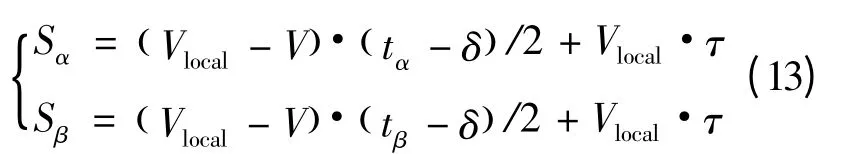
式中:V ＞Vmax。

假设系统分析车辆两难区状态时，激活时间后车辆与停车线之间的距离S'以及接近速度V都是随机变量，且位置与速度相互独立，其概率密度函数分别为f(S')、f(V)，则:

增益概率为:

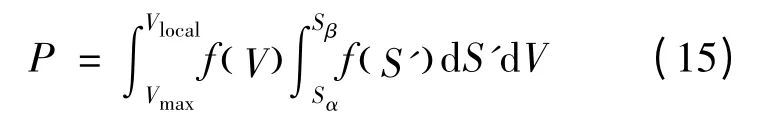
本文将P≤0.001 约定为小概率事件，当系统激活时间增加1 s 时，若P≤0.001，表明延长激活时间后增益不明显，激活时间将维持原值;否则，系统激活时间增加1 s 并再次检验P，直至小概率事件出现［13］。

情形2 接近速度小于(w+L)/γ，加速后不小于(w+L)/γ

在这一情形下，应依据式(4)确定激活时间。由式(1)和式(7)得，两难区存在的条件为:

且当:( τ +γ－δ)2－2( w+L )/dmax＜0 成立时式(16)恒成立，即两难区恒存在，整理得:

(1)恒存在两难区

依据式(3)，当情形2 出现时，若激活时间t有解，接近速度至少需满足:

且:

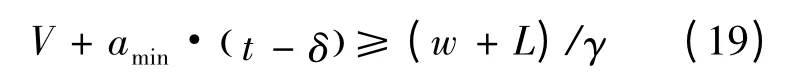
依据式(17)不等号右边项，可得式(19)不等号右边项不小于式(18)不等号右边项，因此，恒存在两难区时，部分车辆的接近速度会导致情形2 出现。具体地，依据式(4)和式(19)可得临界速度Vlimit，当Vlimit≤V ＜(w+L)/γ 时，情形(2)出现，其中:

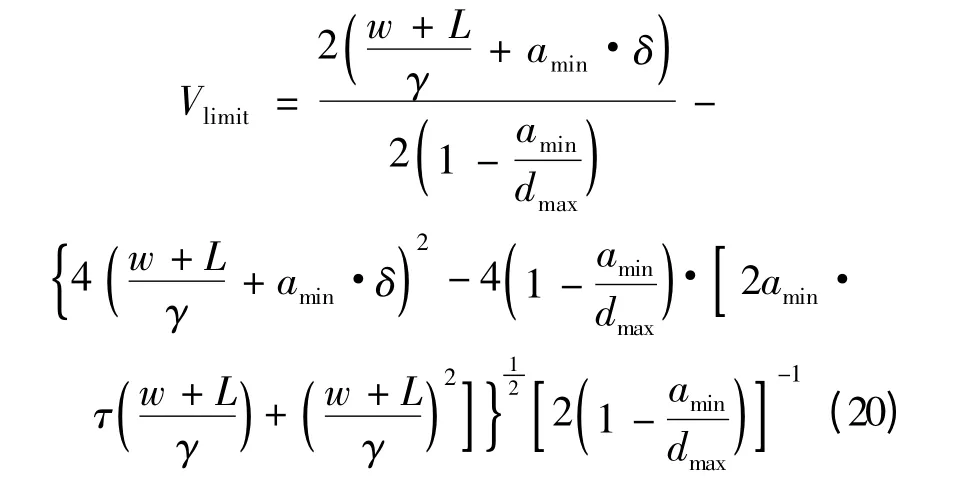
(2)不恒存在两难区

在这一情形下，若情形2 出现，则要求(w+L)/γ ＞2d(τ－δ)。依据式(4)和式(19)，情形2出现的条件为存在两难区且V 属于［Vlimit，(w+L)/γ］。

结合情形1 中的分析，无论是否恒存在两难区，激活时间均需依据式(4)计算，并且由于情形2 出现时V ＞2d(τ－δ)，结合对式(4)的分析，这一区间的接近速度正比于激活时间，因此，情形1下计算得出的激活时间可以引导情形2 中的车辆通过交叉口，即恒有t1＞t2。

情形3 接近速度小于(w+L)/γ，加速后仍小于(w+L)/γ

在这一情形下，两难区存在条件与情形2 的一致，不同的是，应依据式(9)确定激活时间。

(1)恒存在两难区

情形3 出现时，加速后的车速仍小于(w+L)/γ，即:

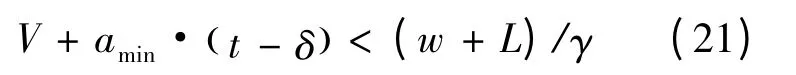
将式(9)代入式(21)得:

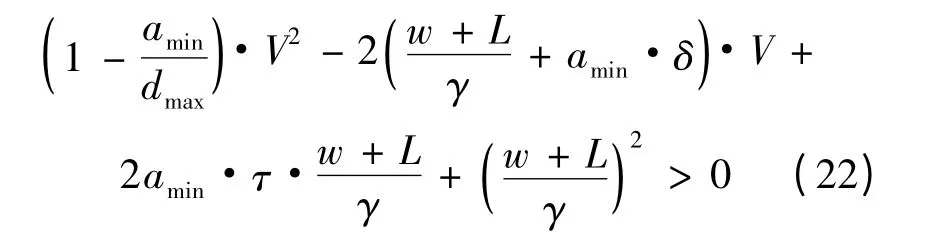
结合对情形2 的分析，恒存在两难区时，2d(τ－δ)＜(w+L)/γ，可证V=(w+L)/γ 时，式(22)左项恒小于0。对于接近速度小于(w+L)/γ 的车辆，依据式(22)可求得一个与情形2 中数值相等的Vlimit，且Vlimit＜(w+L)/γ;当恒存在两难区且V ∈(0，Vlimit)时，情形3 出现。依据式(9)，激活时间t3=max{(t| V=0)，(t| V=Vlimit)}。

(2)不恒存在两难区

这一情形下，式(16)有两实根Vlower、Vupper。(w+L)/γ 与2d(τ－δ)之间的关系决定了(w+L)/γ与Vlower、Vupper间的大小关系。若(w+L)/γ ＞2d(τ－δ)，则情形3 出现的条件为存在两难区且V ∈(0，Vlimit)。依据式(9)，激活时间取两难区存在的速度区间端点对应函数值的最大值。

若(w+L)/γ ≤2d(τ－δ)，则(w+L)/γ ∈(Vlower，Vupper)，且情形3 出现时，V ∈(0，Vlower)，激活时间t3=(t|V=0)。

根据以上的分析，应用加速策略时需要的激活时间tacc应取情形1 和情形3 中的最大值，即tacc=max{t1，t3}。

3.2 应用减速策略时所需激活时间的确定方法

当车辆不具备加速条件时，系统将为车辆提供一个减速策略。由于接近速度V ＜(w+L)/γ时，上述情形2 和情形3 中确定的激活时间能够保证满足该速度条件的车辆通过加速引导规避两难区。因此，接近速度V ＜(w+L)/γ 时，不需要再计算应用减速策略需要的激活时间。对于接近速度同时满足V ＞(w+L)/γ 和V ＞2d(τ－δ)(两难区存在条件)，并且在黄灯启亮时将位于两难区右边界(图2 中B 点)的车辆，由式(6)可知，当车 速 满 足V ∈［max{2dmax(τ － δ)，(w +L)/γ}，Vlocal］时，激活时间t 关于车速V 是单调递增的，因此，为了可减速引导的车辆的接近速度范围更大，激活时间确定为tdec=(t|V=Vlocal)。基于此确定的激活时间能够保证加速前接近速度大于(w+L)/γ，并且速度满足两难区存在条件的车辆，在不具备加速条件时，都可以有一个减速的引导策略。最后，两难区引导系统的激活时间应确定为t=max{tacc，tdec}。

4 算例分析

首先，计算应用加速策略时情形1 对应的激活时间t1。根据式(4)，在黄灯启亮时位于两难区左边界的车辆可以使用acomfort(0.315 m/s2)加速后不超过Vlocal(27 m/s)，且通过交叉口的最大临界速度Vmax=22.78 m/s，对应的激活时间ttemp=14.4 s。考虑到信号控制方案中各信号时长一般为整数，为了实现统一和增加可操作性，对激活时间作向上取整处理，即ttemp=15 s，对应的最大临界速度Vmax=22.85 m/s。假设接近速度、黄灯启亮时车辆与交叉口之间的距离分别服从正态分布N ～(24，32)、N～(35，232)［14］，依据提出的增益模型，计算激活时间延长后的增益概率，结果如图4 所示。

从图4 可以看出，激活时间由15 s 延长至26 s 的过程中，每个时间步长内系统的增益概率逐渐降低，并向0 趋近。其中，16 s 时增益概率P=2.02×10－4，低于0.001，意味着激活时间由15 s延长至16 s 时，系统获得增益的可能性很低。因此，系统激活时间维持t1=15 s 不变。由于情形1中计算的激活时间能够引导情形2 中的车辆通过交叉口，因此，情形2 下的激活时间不予计算。

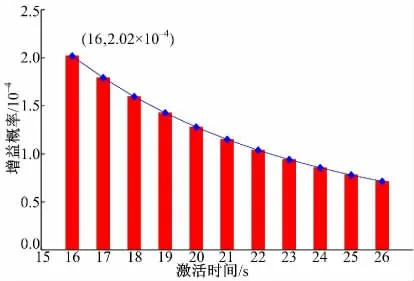
图4 激活时间与增益概率变化趋势Fig.4 Variation between activation time and gain probability

图5 (a)描绘了激活时间为15 s、速度为22.85 m/s且将在黄灯启亮时位于两难区左边界的车辆以0.295 m/s2的加速度加速并通过交叉口时的行驶轨迹。如图5(b)所示，激活时间由15 s缩短至14 s 时，该车辆在黄灯启亮时驶入可通行区并在红灯启亮前通过交叉口所需的最小加速度为0.335 m/s2，不满足驾驶员舒适性，这与图3 中反映的对于同一车辆，激活时间越小所需最小加速度越大的结论一致。

其次，计算应用加速策略时情形3 下的激活时间t3，由于(w+L)/γ=18 m/s，dmax(τ+γδ)2/(2γ)=12 m/s，因此，给定的参数满足式(17)，即情形3 下恒存在两难区，依据式(18)可求得Vlimit=13.82 m/s;。依据式(8)可求得(t|V=0)=11.9 s，(t|V=Vlimit)=6.2 s。因此，情形3下系统激活时间t3=max{(t|V=0)，(t|V=13.82)}=11.9 s，即当系统激活时间不小于11.9 s 时，对于接近速度较低、黄灯启亮时陷入两难区且使用acomfort加速后速度不超过18 m/s 的车辆，引导系统可通过加速策略引导其通过交叉口。结合情形1 和情形3 的计算结果，应用加速策略时所需的激活时间tacc=max{t1，t3}=15 s。

再次，依据式(6)计算得到应用减速策略时所需的激活时间tdec=(t|V=27)=6.5 s。

最后，若在给定的交叉口布设两难区引导系

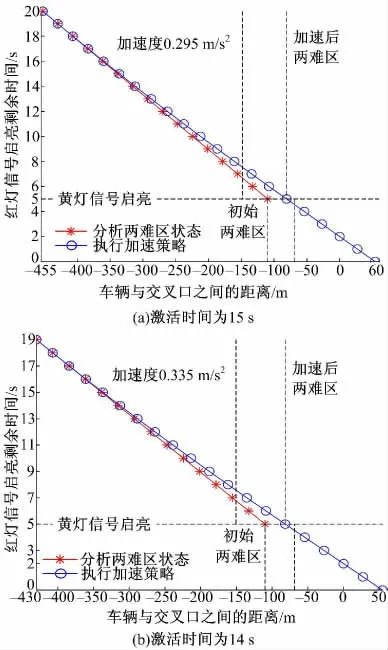
图5 不同激活时间对应的车辆行驶轨迹Fig.5 Vehicle trajectories under different activation time统，系统激活时间应设置t=max{tacc，tdec}=15 s。

5 结束语

在描述基于提前引导的两难区规避系统的基础上，分析了系统激活时间对车辆引导的影响:激活时间越长，系统可加速或减速引导的车辆的速度范围越大，但可能会增加系统布设成本。系统激活时间越短，可能导致部分车辆因加速策略中加速度不满足舒适条件而放弃加速，增加车辆停车等待产生的时间延迟。对于属于不同范围的接近速度，应用加速策略或减速策略所需的激活时间也不同，文中对此进行了分类讨论，并提出了激活时间的确定方法。算例分析表明，本文方法可以确定合理的系统激活时间，为智能交通环境下两难区引导系统的布设提供了依据。

［1］Sharma A，Bullock D，Peeta S.Estimating dilemma zone hazard function at high speed isolated intersection［J］.Transportation Research Part C:Emerging Technology，2011，19(3):400-412.

［2］Zegeer C V.Effectiveness of green-extension systems at high-speed intersections，research report 472［R］.Lexington:Kentucky Department of Transportation，1977.

［3］Yi P.Application of IntelliDrive information system to enhance high-speed safety［J］.Journal of Transportation Research Board，2011，2215:105-112.

［4］Li P F，Abbas M M，Pasupathy R，et al.A new dilemma zone protection algorithm based on the vehicle，trajectories prediction and markov process［C］∥Transportation Research Board 89th Annual Meeting，Washington DC，2010.

［5］储浩，杨晓光，朱彤，等.基于智能车路系统的交叉口主动交通安全技术研究［J］.交通与计算机，2008，26(4):135-139.Chu Hao，Yang Xiao-guang，Zhu Tong，et al.Active traffic safety technology in intersection based on intelligent vehicle-infrastructure syste［J］.Journal of Transport Information and Safety，2008，26(4):135-139.

［6］Si J，Urbanik T，Han L.Effectiveness of alternative detector configurations for option zone protection on highspeed approaches to traffic signals［J］.Transportation Research Record，2007，2035:107-113.

［7］Gozalvez J，Sepulcre M，Bauza R.IEEE 802.11p vehicle to infrastructure communications in urban environments［J］.IEEE Communications Magazine，2012，50:176-183.

［8］Yang D，Jia H F，Tang M.Realization of a dilemmazone guiding algorithm at signalized intersections［J］.IEEE Transactions on Intelligent Transportation Systems，2014:2333-2339.

［9］Moon Y J.Functional requirements for in-vehicle dilemma zone warning system at signalized intersections［J］.Transportation Research Record，2002，1800:62-68.

［10］Rajesh R.Vehicle Dynamics and Control［M］.New York:Springer-Verlag，2011.

［11］Liu C，Herman R，Gazis D.A review of the yellow interval dilemma［J］.Transportation Research Part A，1996，30(5):333-348.

［12］ISO2631-1-1997.Mechanical vibration and shock-evaluation of human exposure to whole-body vibration-part 1:general requirements［S］.

［13］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京:高等教育出版社，2008.

［14］Saito T，Ooyama N，Sigeta K.Dilemma and option zones，the problem and countermeasures-characteristics of zones，and a new strategy of signal control for minimizing zones［C］∥Third International Conference on Road Traffic Control，London，1990:137-141.