幂函数过渡段复合变幅杆振动特性的研究
2015-06-12张宁宁
□ 张宁宁
渭南师范学院 物理与电气工程学院 陕西渭南 714000
功率超声振动系统通常是由超声变幅杆、换能器和工具杆组成,其中变幅杆是决定聚集能量和放大振幅的最关键元件。目前对于各种单一形状及其不同组合的变幅杆研究较多[1-6],但对于三段以上变幅杆计算各性能参数时,如应用传统计算方法,各参数的求解繁琐、复杂。本文应用传输矩阵方法[5],计算复合三段式幂函数变幅杆的频率方程和放大系数,并以前后段长度相等为例作进一步分析,利用ANSYS软件进行模态分析,结果表明,谐振频率和放大系数模拟值与计算值误差都较小,说明本文理论的正确性,其结果可为此类变幅杆的频率修正提供理论依据和参考。
1 幂函数形复合变幅杆理论分析
图1为幂函数形复合变幅杆的示意图,其中Ⅰ和Ⅲ为等截面棒大小段部分,Ⅱ为幂函数形变截面棒部分,大小端横截面积分别为 s1、s2,其面积函数为 s(x)=将作用在变幅杆输入端及输出端的力及振动速度分别记为 F1、、 F2、, 幂函数截面半径为:(其中形状参数a=(N-1),大小端半径比
单一幂函数形变幅杆的等效四端网络各参量分别为 [7]:
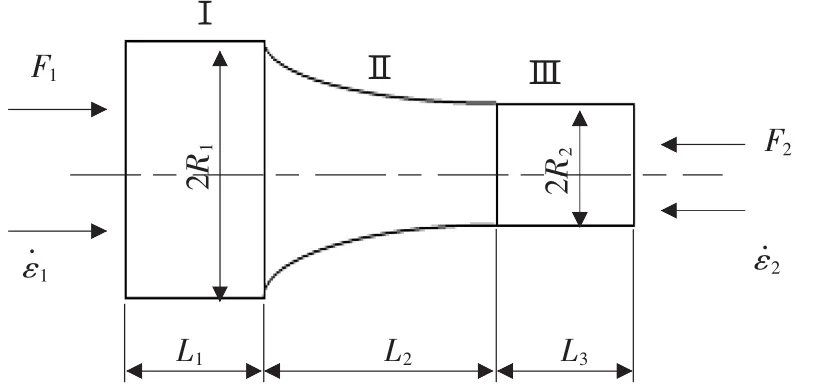
▲图1 幂函数形复合变幅杆
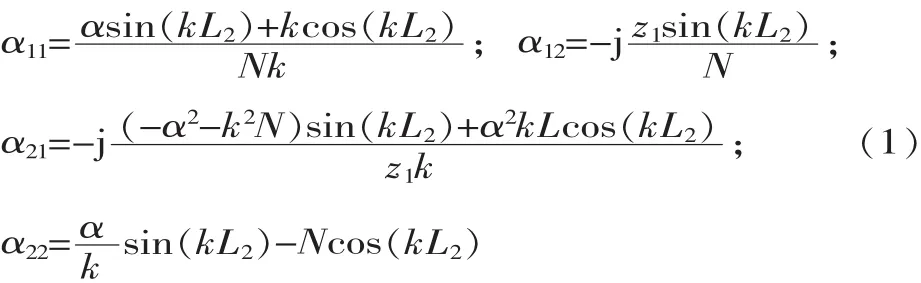
应用传输矩阵理论[5]可得到如下关系式:

式中:k 为波数;z1=ρCs1,z2=ρCs2,ρ、C 分别为材料密度及纵波速度;A11、A12、A21、A22分别为复合变幅杆的等效四端网络各参量。
当两边界自由时,即F1=F2=0,得A12=0,通过矩阵运算可得:
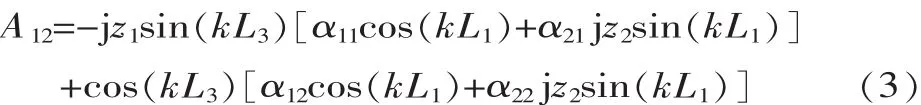
由此可得到具有幂函数过渡段形状的阶梯形变幅杆频率方程:
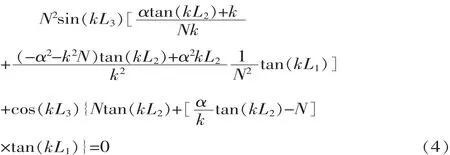
同理由矩阵运算得放大系数为:
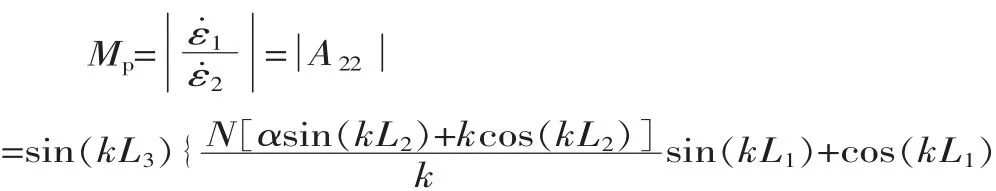

2 数值分析
两端长度相等而截面不同的阶梯形变幅杆,它的振幅放大系数最大[8],因此研究kL1=kL3的具有幂函数形过渡段的阶梯形复合变幅杆显得更具有实际意义。作为例子,对kL1=kL3的复合变幅杆进行分析,将kL1=kL3代入式(4),其频率方程变为:
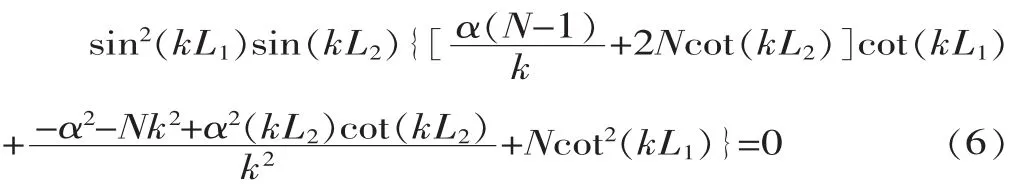
以N为参变量,由上式即可描绘出在谐振条件下变幅杆过渡段参数kL2与阶梯杆参数kL1之间的相互关系曲线,如图2所示。由图可知,当kL2<1.5时,随N的增大,kL1随kL2的增大而下降较快,当kL2>1.5 时,随N的增大,kL1随kL2的增大而下降较慢,并且 N愈大,这种现象愈明显。
同样把kL1=kL3代入式 (5),其振幅放大系数变为:
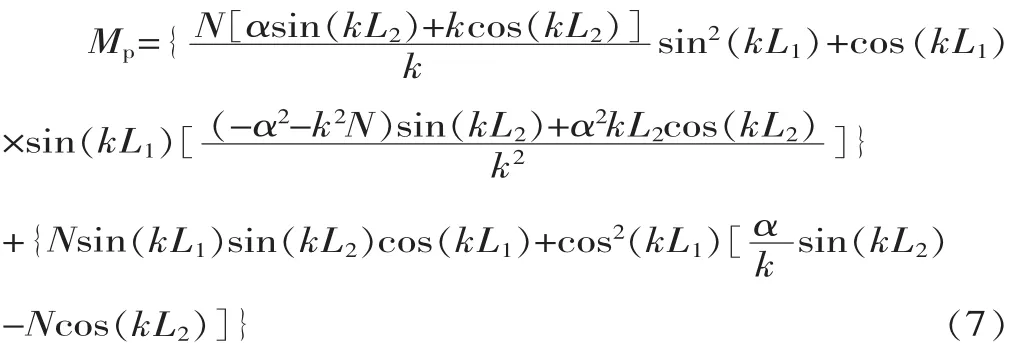
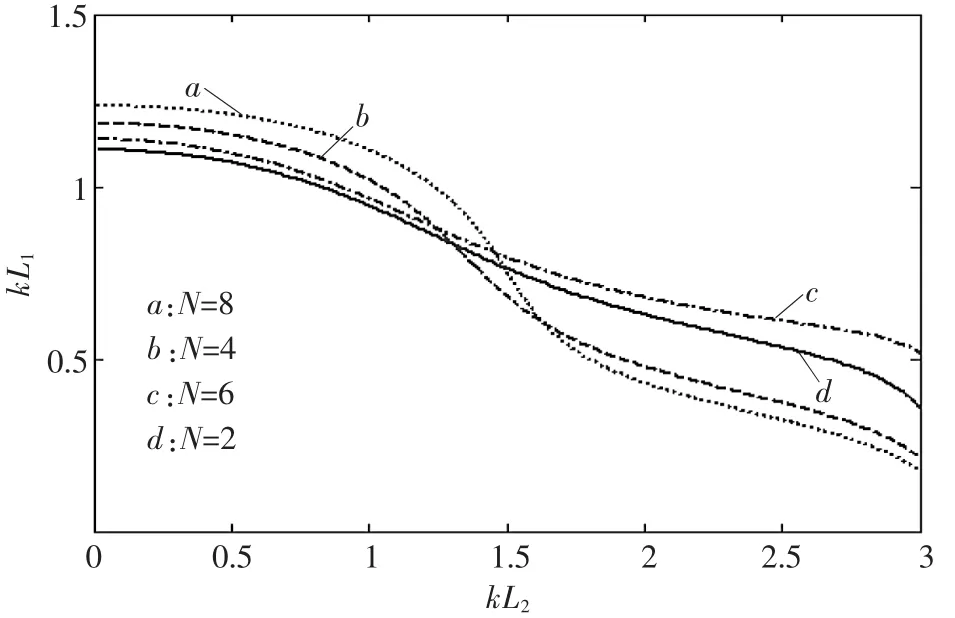
▲图2 谐振条件下kL1与kL2的关系曲线族
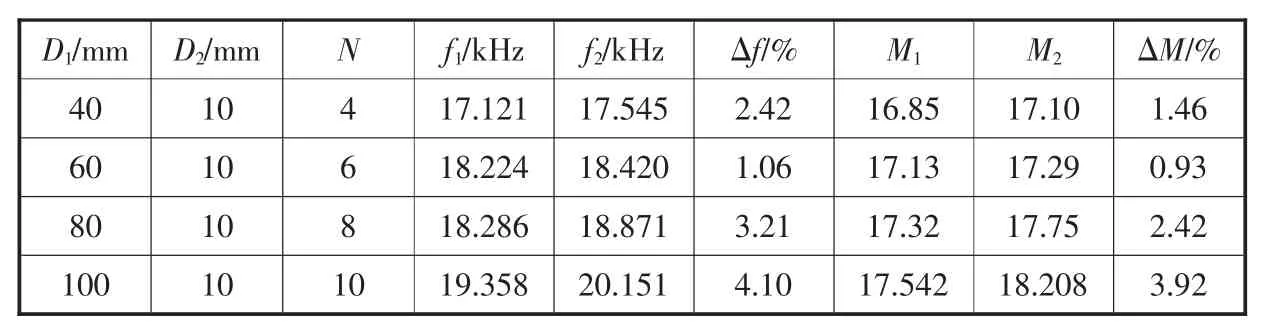
表1 N不同时模拟值与计算值的比较

表2 N相同、L2不同时模拟值与计算值的比较
为了验证本文中所得结论的准确性,取变幅杆材料为45号钢,杨氏模量E=216 GPa,泊松比σ=0.28;密度 ρ=7.84×103kg/m3。 用 ANSYS有限元模态分析,并与理论值进行比较,表1为N不同时模拟值与计算值的比较,表2为N相同、L2不同时模拟值与计算值的比较。表中:D1和D2分别为变幅杆大端和小端的直径,f1和f2分别代表理论计算频率和ANSYS模拟频率,是频率的相对误差,M1为理论放大系数,M2为模拟放大系数,为放大系数的相对误差。
由表1可以看出,随着N的增加,频率与放大系数都在增大,通过比较还可以看出,不论是谐振频率还是放大系数,模拟值与计算值的相对误差都较小,表明本文理论的正确性。由表2可以看出,当N相同、过渡段长度L2不同时,谐振频率与放大系数的模拟值与计算值的相对误差还是较小,同时还可以看出,随着L2的增加,谐振频率和放大系数都不断减小,这为此类变幅杆的频率修正提供了理论依据和参考[9-13]。
3 结论
利用传输矩阵推导了幂函数形复合变幅杆的频率方程和放大系数,分析了过渡段对放大系数及频率特性的影响,在此基础上又用有限元软件ANSYS进行了模态分析,验证了本文计算的正确性,与数值法相比,大大简化了计算过程,物理意义也比较明显。
[1] 万德安,刘春节.超声变幅杆的模态分析[J].机械与电子,2004,33 (4):l0-13.
[2] 阮世勋.超声弯曲谐振杆准确计算和应用的几个问题[J].应用声学,1990,9(4):29-34.
[3] 林书玉.纵一扭复合振动模式指数型复合超声变幅杆的研究[J].应用声学,1997,16(5):42-46.
[4] K H j Seah,Y S Wong,L C Lee.Design of Tool Holders for Ultrasonic Machining Using FEM [J] .Journal of Materials Processing Technology,1993,37:801-816.
[5] 高洁.复合多段式变幅杆优化设计及声学特性分析[J].陕西师范大学学报 (自然科学版),2006,34(4):44-46.
[6] 林忠茂.超声变幅杆的原理和设计[M].北京:科学出版社,1987.
[7] 高健,晨曦.大尺寸矩形截面幂函数复合变幅杆的研究[J].声学技术,2009,28(6):807-810.
[8] 梁召锋,林书玉.余弦形过渡段阶梯形变幅杆研究[J].陕西师范大学学报(自然科学版),2003,31(4):34-35.
[9] 许龙,林书玉.幂函数超声变幅杆的研究[J].陕西师范大学学报(自然科学版),2007,35(5):49-51.
[10]姚文苇,林书玉,王亚雄.指数形负载超声变幅杆频率方程与放大系数的研究[J].陕西师范大学学报(自然科学版),2005,33(3):53-54.
[11]贺西平,程存弟.几种常见形状函数超声变幅杆性能参量的统一表达式[J].陕西师范大学学报(自然科学版),1994,22(3):29-32.
[12]林书玉.超声换能器的原理及设计[M].北京:科学出版社,2004.
[13]原丰霞,张慧君,朱国良.基于ANSYS的超声变幅杆的优化设计[J].机械工程师,2004(11):24-26.
