任意边界条件三维弹性矩形厚板结构振动分析

张羽飞，杜敬涛，杨铁军，朱明刚，刘志刚

(哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨150001)

在工程实际中，研究矩形板结构的振动问题具有重要意义，国内外众多学者开展了研究工作。在现有研究中，大多数分析方法都是基于经典板理论或相关近似算法，如经典板理论、一阶剪切变形板理论以及高阶剪切变形板理论。

近几十年来，忽略剪切变形的经典薄板理论广泛用于板结构振动分析，Leissa等［1-2］基于该理论在研究任意边界条件薄板振动特性领域做出了卓越贡献。然而，随着板厚度增加，经典板理论由于忽略剪切变形将会导致计算频率高于振动系统的真实频率。1951年，Mindlin等首先提出采用三维弹性理论分析板振动问题［3-4］，他在经典理论基础上引入修正系数κ近似剪切变形。但是这种假设与板结构厚度方向剪切应力的实际分布存在差异，计算结果不包括系统在厚度方向的对称模态，分析厚板振动特性效果较差。

基于三维弹性理论厚板结构振动分析日益为人们所关注。虽然有限元法能够对此类问题求解，然而由于随着分析频率升高需要网格加密，以及几何参数改变时需要重新建模等不足，不能很好满足人们对三维厚板振动问题的分析与优化。文献［5-12］应用微分求积法分析了经典边界条件板结构三维振动特性。Leissa等［13-14］使用里兹法求解了矩形厚板模态特性。杨正光等［15］采用状态方程法获得了简支边界功能梯度三维矩形板自由振动精确解。杨亚政等［16］给出了四边简支各向同性层合板自由与强迫振动表达式。现有研究多是针对对称经典边界，选取适当的基函数以满足边界条件，并不能灵活地适应边界条件的改变及约束刚度变化。

近来，文献［17-18］采用二维改进傅里叶级数法对弹性边界约束下矩形薄板结构的面内振动与弯曲振动问题进行了分析。本文将二维改进傅里叶级数法扩展为三维，对矩形厚板结构沿3个坐标轴方向的位移场进行建模，并应用瑞利－里兹法求解未知傅里叶系数，分析了三维弹性矩形厚板的自由及强迫振动特性。通过与现有文献中的结果以及NASTRAN软件计算结果进行对比，验证了本方法的有效性和正确性，并且不受边界条件的限制。

1 三维弹性矩形厚板建模

1.1 问题描述

如图1所示，矩形厚板长度为a，宽度为b，厚度为c(在三维弹性理论框架下，当厚度很大时，可以代表更为一般的三维弹性体)。根据三维弹性理论应力状态，在边界表面任一点处存在正应力和另外2个方向的切应力，为此相应引入3个方向的线性弹簧，以实现边界约束的平衡/协调条件，通过调节弹簧的刚度值可以实现任意经典边界条件及其组合。其中，约束边界表面上的任意点位置均存在沿3个坐标轴方向分布的3种类型约束弹簧。例如，k1y1和k3y1表示分布在y=b边界上的切向约束弹簧，k2y1表示法向约束弹簧。

图1 三维弹性矩形厚板模型及坐标系统Fig.1 Three-dimensional elastic thick plate and the coordinate system

在矩形板三维振动分析中，边界约束通常施加在x=0，a和y=0，b这4个侧面位置，其余2个面处于自由状态。以y=b边界表面为例，各种经典边界条件表示如下:

1.2 三维位移场的改进傅里叶级数描述

最近，文献［19］以封闭舱室空间噪声预报为背景，成功地提出任意阻抗壁面条件下矩形封闭空间声学特性分析的三维改进傅里叶级数法，本文将该方法进一步拓展应用至矩形厚板结构的三维振动分析问题，即矩形厚板结构中沿3个不同坐标轴方向的振动位移场函数可以表示为

式中:λamx=mxπ/a，λbmy=myπ/b，λcmz=mzπ/c。这里引入6个补充函数是为了克服三维厚板结构的位移函数在6个边界表面可能存在的求导不连续，这样，位移函数就可以满足任意的边界条件，并且将显著改善解的收敛性。

1.3 三维板结构振动问题求解

本文将采用基于能量原理的瑞利－里兹方法对未知系数进行求解。三维矩形厚板系统拉格朗日函数可以写为

式中:V表示系统总势能，T表示系统总动能，Wext表示外部激励对板结构所做的功。

根据三维弹性力学理论，总势能可以表示为

式中:G为剪切刚度，μ为泊松比。在任意边界条件下分析厚板结构的振动特性仅需改变上式中的边界约束弹簧刚度系数即可。

厚板结构的总动能为

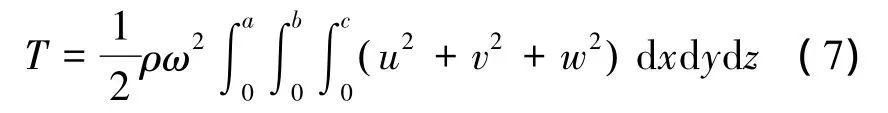
式中:ρ为板结构的密度，ω表示振动角频率。

在板结构上施加一个集中力F，则外部激励对板结构所做的功可以表示为

式中:Fx、Fy及Fz分别表示力向量沿x、y及z轴方向的分量，(xe，ye，ze)表示其作用位置。

将位移函数(4)代入系统拉格朗日函数(5)中，通过瑞利－里兹法即可得到关于傅里叶级数的未知系数的21个线性方程。厚板结构系统振动微分方程可以进一步写成矩阵的形式:

通过求解系统方程(9)，即可获得板结构位移响应函数中的所有未知系数，进一步将方程等号右边的力向量设置为零，通过求解标准矩阵特征值问题，还可以求得三维矩形厚板结构的模态参数。将各阶特征向量代入式(4)的位移函数中，便可得到各个固有频率下的模态振型分布。

2 计算结果及分析

本节将会给出一些具体的数值算例，首先对本方法的有效性进行验证，接着再对矩形厚板结构的三维振动进行进一步的分析。在所有算例中，矩形厚板在x轴方向的长、宽、高分别为a、b、c，材料参数分别为:杨氏模量 E=7×1010N/m2;密度 ρ= 2 700 kg/m3以及泊松比μ=0.3。频率参数采用文献中通常使用的γ，其定义为

式中:D=Ec3/[12( 1－μ2)]表示板结构的抗弯刚度。

2.1 全自由边界下矩形厚板自由振动

首先考虑完全自由的边界条件，即所有边界约束弹簧的刚度值设置为零的情况。在实际计算中，3个方向上的位移仅包括前(Mx+1)×(My+1)×(Mz+ 1)项，一般来讲，如果模型的三边相对几何尺寸增大，某一方向上的傅里叶级数截断数也要随之增加，以保证解的快速收敛性。表1中的数值计算结果为满足2种不同厚宽比的FFFF方形板的频率参数，截断数设置为Mx=My=10，Mz=5。通过对比可见，现有理论计算结果与文献中数据及有限元计算结果吻合良好，而与经典板理论计算结果相差较大;当厚度进一步增加至一般弹性体情况时，可以发现本文方法依然有效，而经典板理论已不能给出此种情况的正确模态参数。

表1 不同厚宽比下FFFF方形板频率参数Table 1 Frequency parameters for square FFFF plate of different aspect ratios

2.2 钳支边界下板自由振动的收敛性

为了检验本方法的收敛性，任意厚宽比下的CCCC方形板模态特性参数列于表2。通过设置所有边界约束弹簧的刚度值为无穷大(实际计算中采用1015)，即可模拟钳支边界。通过与文献［14］及NASTRAN计算的结果对比可见，对于任意厚度的CCCC方形板，本方法结果收敛迅速。为了获得较为精确的结果，傅里叶级数的截断数应随着板结构厚度方向的几何尺寸一同改变。表中还给出了经典板理论计算结果，通过对比可见，不考虑板结构厚度方向分布的剪切应力会导致计算结果偏大。

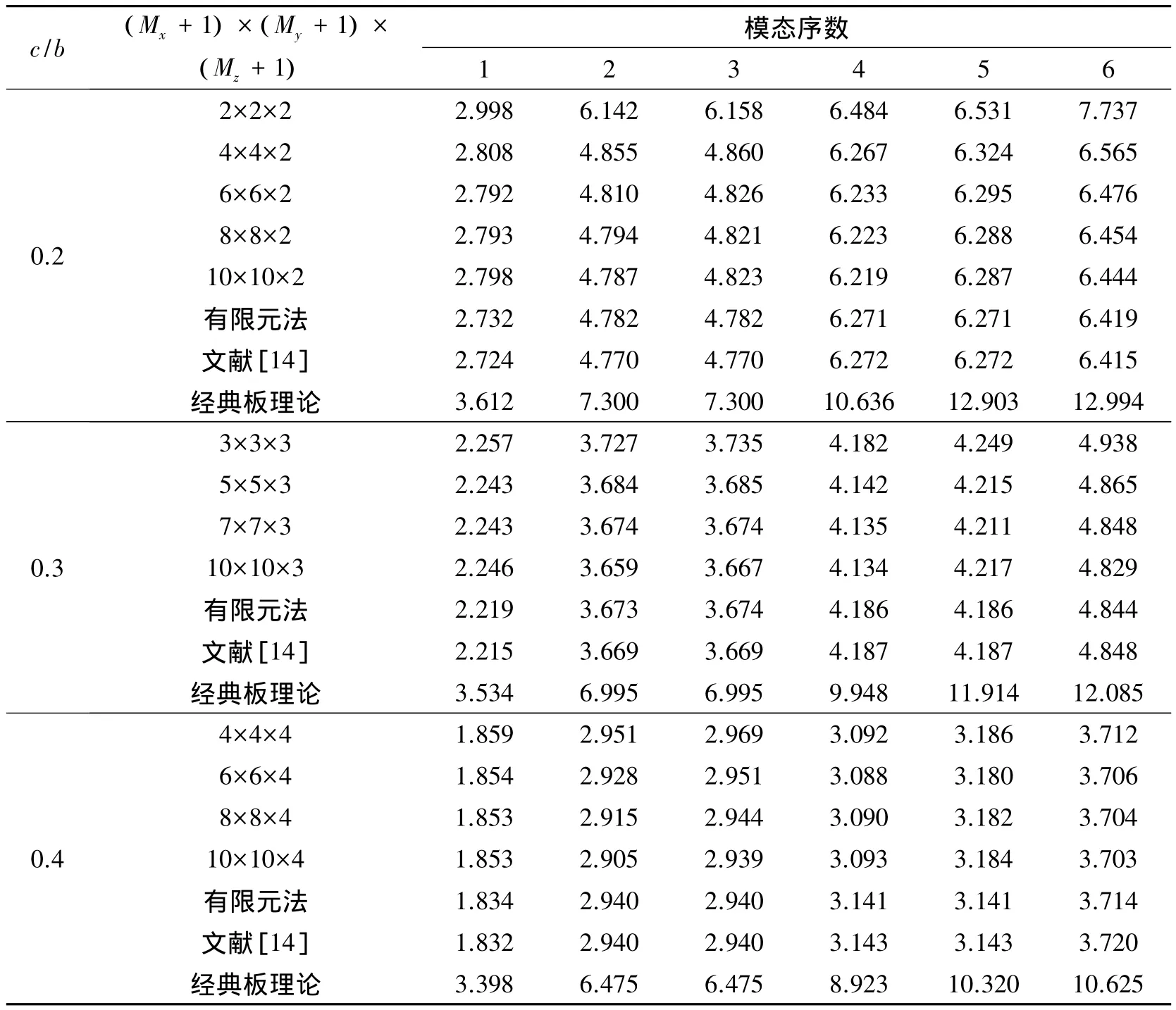
表2 任意厚宽比下CCCC方形板频率参数Table 2 Frequency parameters for square CCCC plate of different aspect ratios

2.3 简支边界下矩形厚板自由振动

另一种经典边界即为简支边界，表3给出了任意厚宽比下SSSS方形板的频率参数。该结果与文献［20］结果和NASTRAN计算结果能够很好的吻合，最大偏差不超过1.4%。

表3 任意厚宽比下SSSS方形板频率参数Table 3 Frequency parameters for square SSSS plate of different aspect ratios

2.4 经典组合边界下矩形厚板振动分析

在现有的文献中，矩形厚板的三维振动分析主要针对于对称边界条件，并且计算过程中，当厚板结构的边界条件发生改变时，需要修改位移函数或理论方程，对问题进行重新推导与求解。本文在矩形板结构的各个边界表面均引入3种约束弹簧，可以简单方便地描述任意类型边界条件，当结构边界条件发生改变时，无需对问题重新推导。接下来给出了厚板结构在非对称边界条件FSSS下的振动特性，见表4。

由表4中的数据可以看出，采用改进傅里叶级数法计算的结果与NASTRAN计算结果吻合良好，证明该方法的有效性和正确性。如理论部分所述，在求解结构模态过程中，将系统控制方程特征向量代入至位移函数中，便可得到各个固有频率下的模态振型分布，图3给出厚宽比c/b=0.3时，FSSS方形板的前6阶模态振型。

表4 任意厚宽比下FSSS方形板频率参数Table 4 Frequency parameters for square FSSS plate of different aspect ratios

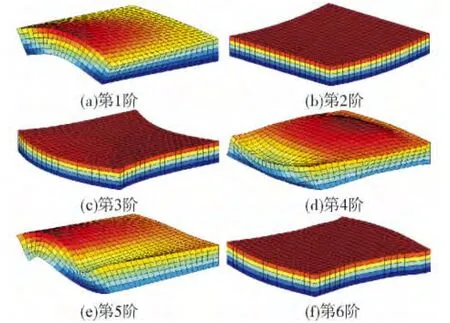
图3 厚宽比c/b=0.3的FSSS方形板前6阶振型Fig.3 The first six mode shapes of FSSS square plates with the aspect ratio c/b=0.3

2.5 弹性约束边界下矩形厚板振动分析

为了更全面地分析矩形厚板结构的三维振动，在下面的算例中，进一步考虑弹性约束边界条件。假设在板结构的4个边界表面上，存在法向约束为零，切向约束为弹性约束，这种弹性约束边界条件表示为SSSS(k)。表5给出了当约束弹簧刚度系数k=1011N/m时，任意厚宽比下SSSS(k)方形板结构的频率参数。表中本方法计算结果与有限元法计算结果吻合良好，这表明，针对弹性约束边界条件来说，本方法是准确有效的，并且具有计算时间短，收敛速度快等优势。

表5 任意厚宽比下SSSS(k)方形板频率参数Table 5 Frequency parameters for square SSSS(k)plate of different aspect ratios

图4给出了厚宽比c/b=0.2的SSSS(k)方形板结构在外力激励下强迫振动加速度响应。其中，F的大小为1 N，沿x轴方向作用于(3a/10，3b/10，0)处。为了避免模态共振处发生数值不稳定的问题，在仿真计算中通过复杨氏模量引入结构阻尼η= 0.01，即Ê=E(1+jη)。通过对比可见，本文方法与有限元法曲线基本吻合，差异主要集中在共振峰处，并且随着频率升高，差距加大，原因是为了缩短计算时间，在使用有限元软件时，不能将网格划分过细，影响了计算精度。

图4 厚宽比c/b=0.2的SSSS(k)方形板(9a/10，9b/ 10，c)处振动加速度响应Fig.4 Vibrational acceleration response at point(9a/ 10，9b/10，c)of SSSS(k)square plates with the aspect ratio c/b=0.2

3 结论

将一种三维改进傅里叶级数法拓展应用于任意边界条件下矩形厚板的振动特性分析，基于三维弹性理论并结合瑞利－里兹法求解了任意边界条件下矩形厚板的自由与强迫振动问题，获得了可靠而有效的计算结果，并得到如下结论:

1)基于三维弹性理论应力状态，为满足弹性边界约束的平衡/协调条件，引入3种类型的线性弹簧，相应改变边界弹簧刚度系数即可实现各种边界条件的任意切换。

2)所构建的改进傅里叶级数位移形式具有良好的收敛特性与预报精度，当厚度进一步增加至一般弹性体时，通过相应增加此方向上的截断项数能够实现本文方法对三维弹性体的振动特性预报。

3)给出了三维矩形厚板在非对称边界条件下的模态数据，本文方法成功避免了当边界条件改变时其它方法所需要对位移函数和理论描述的形式修改与重新推导，相比文献中的计算方法更加简便直观，更为适合三维矩形厚板振动特性分析。

4)求解了矩形厚板结构在弹性约束边界条件下自由及强迫振动问题的解析解，为后续工程中相关厚板结构振动特性分析及响应快速预报提供了有力手段。

［1］LEISSA A W.The free vibration of rectangular plates［J］.Journal of Sound and Vibration，1973，31(3):257-293.

［2］LEISSA A W.Recent research in plate vibrations:classical theory［J］.The Shock and Vibration Digest，1977，9(10): 13-24.

［3］MINDLIN R D.Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates［J］.ASME Journal of Applied Mechanics，1951，18(1):31-38.

［4］MINDLIN R D，SCHACKNOW A，DERESIEWICZ H.Flexural vibrations of rectangular plates［J］.Journal of Applied Mechanics，1956，23:430-436.

［5］BELLMAN R，CASTI J.Differential quadrature and longterm integration［J］.Journal of Mathematical Analysis and Applications，1971，34(2):235-238.

［6］BELLMAN R，KASHEF B G，CASTI J.Differential quadrature:a technique for the rapid solution of nonlinear partial differential equations［J］.Journal of Computational Physics，1972，10(1):40-52.

［7］CIVAN F，SLIEPCEVICH C M.Application of differential quadrature to transport processes［J］.Journal of Mathematical Analysis and Applications，1983，93(1):206-221.

［8］MALIK M，BERT C W.Three-dimensional elasticity Solutions for free vibrations of rectangular plates by the differential quadrature method［J］.International Journal of Solids and Structures，1998，35(3/4):299-318.

［9］LIEW K M，HUNG K C，LIM M K.Three-dimensional vibration of rectangular plates:Variance of simple support conditions and influence of in-plane inertia［J］.International Journal of Solids and Structures，1994，31(23):3233-3247.

［10］LIEW K M，HUNG K C，LIM M K.Free vibration studies on stress-free three-dimensional elastic solids［J］.Journal of Applied Mechanics，1995，62(1):159-165.

［11］LIEW K M，HUNG K C，LIM M K.Three-dimensional vibration of rectangular plates:effects of thickness and edge constraints［J］.Journal of Applied Mechanics，1995，182 (5):709-727.

［12］HAN J B，LIEW K M.Numerical differential quadrature method for Reissner/Mindlin plates on two-parameter foundations［J］.International Journal of Mechanical Sciences，1997，39(9):977-989.

［13］LEISSA A，ZHANG Zhongding.On the three-dimensional vibrations of the cantilevered rectangular parallelepiped［J］.Journal of the Acoustical Society of America，1983，73(6):2013-2021.

［14］ZHOU D，CHEUNG Y K，AU F T K，et al.Three-dimensional vibration analysis of thick rectangular plates using Chebyshev polynomial and Ritz method［J］.International Journal of Solids and Structures，2002，39(26):6339-6353.

［15］杨正光，仲政，戴瑛.功能梯度矩形板的三维弹性分析［J］.力学季刊，2004，25(1):15-20.

YANG Zhengguang，ZHONG Zheng，DAI Ying.Three dimensional elasticity analysis of a functionally graded rectangular plate［J］.Chinese Quarterly of Mechanics，2004，25(1):15-20.

［16］杨亚政，刘华.层合板自由振动和强迫振动的三维精确解［J］.力学与实践，2008，30(1):23-26.

YANG Yazheng，LIU Hua.Three-dimensional exact solution for free and forced vibrations of multilayered plates［J］.Mechanics in Engineering，2008，30(1):23-26.

［17］DU Jingtao，LI W L，JIN Guoyong，et al.An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges［J］.Journal of Sound and Vibration，2007，306(3/4/5):908-927.

［18］LI W L，ZHANG Xuefeng，DU Jingtao，et al.An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports［J］.Journal of Sound and Vibration，2009，321(1/2):254-269.

［19］DU J T，LI W L，LIU Z G.Acoustic analysis of a rectangular cavity with general impedance boundary conditions［J］.The Journal of the Acoustical Society of America，2011，130(2):807-817.

［20］LIM C W，LIEW K M，KITIPORNCHAI S.Numerical aspects for free vibration of thick plates Part I:Formulation and verification［J］.Computer Methods in Applied Mechanics and Engineering，1998，156(1/2/3/4):15-29.