挖掘机动臂结构应力分布快速预测
2015-06-12沈振辉杨拴强沈培辉
沈振辉, 杨拴强, 沈培辉
(1.福建江夏学院,福建 福州 350108;2.福建船政交通职业学院,福建 福州 350007)
0 引 言
动臂是挖掘机工作装置主要构件之一。动臂结构的应力响应不仅是评价结构设计是否合理的重要标准之一,也是结构优化设计的主要约束条件之一。然而,现有的研究方法在求解结构应力时普遍存在以下问题:
1)对于结构复杂的机械零部件,直接建立结构应力响应函数难度大,求解困难,采用结构有限元分析的方法能够降低结构应力求解难度,在一定程度上提高求解效率,但现有结构优化方法中,对结构应力的求解采用循环调用有限元分析软件重复进行实体建模、网格划分、边界加载、分析计算、结果提取等过程[1-2],系统建模难度大,求解效率低;
2)为降低建模难度,提高建模效率和求解速度,对模型进行简化和降阶的方法得到了广泛应用[3-7],但此方 法 降 低 了 求 解 精 度,甚 至 形 成“人为”应力集中点,且依然无法避免优化过程中对有限元分析模块的频繁调用,无法形成真正意义上的高效分析;
3)人工神经网络与通用有限元分析相结合方法显著提高了结构优化求解效率[8-10],但动臂属复杂机械结构件,各结构变量间受几何形状约束耦合性强,缺乏有效的神经网络训练教师样本抽样方法,样本分布均匀性差、代表性差,且现有结构应力神经网络预测模型只能预测结构最大应力,难以预测结构应力分布状态。动臂虽属复杂机械结构,但不同结构驱动参数及不同工况下,应力最大值出现的位置依然具有典型的规律性。通过提取可能出现结构最大应力值的特征区域,能够实现对动臂结构应力分布的预测。
综合上述分析,探讨高效、可靠的神经网络预测模型教师样本抽样方法和动臂结构应力特征区域提取方法,研究动臂结构应力分布快速预测机制,构建动臂结构应力分布快速预测模型,具有重要的理论与现实意义。
1 应力分布快速预测机制
针对现有动臂结构应力响应求解存在求解机制复杂、求解效率低、难以快速求解结构应力分布状态,结构抽样中样本代表性差,分布均匀性差等不足,基于神经网络模型的结构应力分布快速预测机制如图1所示。
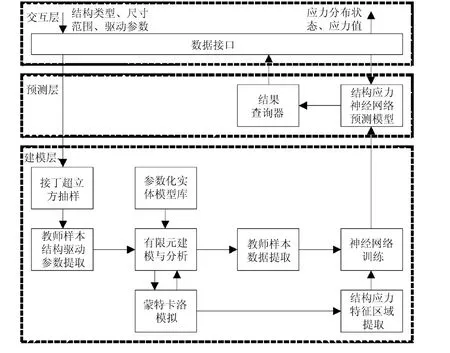
图1 结构应力分布快速预测机制框架
图1 中,结构应力分布的预测机制由交互层、预测层和建模层组成。交互层提供良好的数据接口,实现工程师及其他模块与系统的交互。预测层是结构应力快速预测的核心层,结构类型、尺寸范围及结构驱动参数等通过交互层输入后传递给预测层,预测层根据结构驱动参数调用结构应力神经网络预测模型快速预测各应力特征区域内应力值,由结果查看器对预测结果进行规整,进而以图表、数据等多种形式将结构应力值及分布状态反馈回交互层。建模层负责完成预测层结构应力神经网络预测模型的建模,包括拉丁超立方抽样、教师样本结构驱动参数提取、参数化实体模型库、有限元建模与分析、蒙特卡洛模拟、教师样本数据提取、结构应力特征区域提取和结构应力神经网络训练等模块。
拉丁超立方抽样不仅具有抽样覆盖面广、效率高、可以实现任何样本容量要求等优点,而且还能有效避免正交设计、均匀设计等方法产生的动臂结构畸形问题。因此,引入拉丁超立方抽样技术能够有效解决现有动臂结构应力预测中存在的教师样本均匀性差、模型泛化性差、预测精度低等不足。
针对现有结构应力预测模型中难以预测结构应力分布情况的不足,通过蒙特卡洛模拟提取动臂结构应力特征区域及各个区域内的局部最大应力值,能够有效预测动臂结构应力分布情况,为动臂结构优化提供重要参考依据。为提高教师样本结构应力计算效率,采用自动化动臂结构有限元建模与分析技术,在参数化实体模型库的基础上,综合利用Pro/Engineer强大的参数化实体建模能力及Pro/TOOLKIT二次开发技术、ANSYS的高效有限元分析能力及其与Pro/Engineer的无缝接口,实现自动化动臂结构的三维实体建模、有限元建模与分析及计算结果的提取。
在上述机制下,将神经网络模型用于结构应力分布快速预测的基本步骤为:
1)通过蒙特卡洛模拟确定动臂结构各应力特征区域;
2)将动臂结构驱动变量作为输入变量,构成人工神经网络的输入层,而将通用有限元分析得到的各应力特征区域局部最大应力值作为输出变量,构成人工神经网络的输出层;
3)根据拉丁超立方抽样确定教师样本,利用自动化动臂结构有限元分析模块对教师样本进行计算,得到教师样本的理论输出;
4)用教师样本的输入和输出训练人工神经网络。这样,人工神经网络就如同一个黑箱模型,只要给定输入,就能得到相应的输出,既可以作为独立程序,也可以嵌入到结构优化程序中。由于教师样本数量远远少于迭代次数,因此,相对于优化迭代过程中频繁调用有限元分析而言,对教师样本进行有限元分析具有工作量小、效率高的优点。
2 动臂结构样本均匀抽样
动臂结构属复杂机械结构,在特定的机构参数条件下,随机组合的结构驱动参数可能导致生成的动臂结构为畸形结构。畸形动臂结构属不合理样本,在进行有限元分析前应予以剔除。直接采用一般随机抽样方法确定动臂结构样本时,剔除不合理动臂结构后难以保证剩余样本集中各样本结构参数分布的均匀性。因此,有必要探讨有效的抽样方法和不合理样本的剔除方法。
确定动臂结构神经网络预测模型教师样本时,样本数量越多,预测精度越高,但过多的样本数量将导致动臂结构有限元分析代价过高。拉丁超立方抽样给出无偏的或偏度很小的系统参数估计值,其方差较之简单的随机采样也显著减小,可以在抽样较少的情况下获得较高的计算精度。由于动臂几何结构约束难以直接用数学模型进行表达,采用拉丁超立方抽样确定动臂结构样本时,畸形动臂结构样本的剔除方法有以下两种:
1)直接抽样法。在所有参数的取值范围内进行拉丁超立方抽样,得到样本集y1。在y1的基础上,剔除结构畸形动臂,从而得到合适规模的样本集y2。
2)分阶段抽样法。在导致动臂结构产生畸形的参数中进行拉丁超立方抽样,得到样本集y1。在y1的基础上剔除结构畸形动臂得到合适规模(设为N个)的相关参数的样本集y2。最后将y2与其它参数联立进行N个样本的拉丁超立方抽样,得到样本容量为N的样本集y3。
为了比较以上两种方法的优劣性,以最简单的二维变量为例进行结构抽样。x1,x2为耦合结构驱动变量,x1∈[5,15],x2∈[10,20]。为模拟几何约束,假设当x2∈[14,16]时结构畸形。采用直接抽样法时,设置初始样本容量为20进行拉丁超立方抽样后,得到样本容量为16的样本集,样本分布散点图及变量抽样频率图如图2所示。
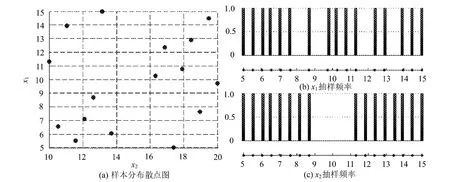
图2 直接抽样法样本分布散点图及变量抽样频率图
采用分阶段抽样法时,设置初始样本容量为20进行拉丁超立方抽样后,得到样本容量为16的样本集,样本分布散点图及变量抽样频率图如图3所示。
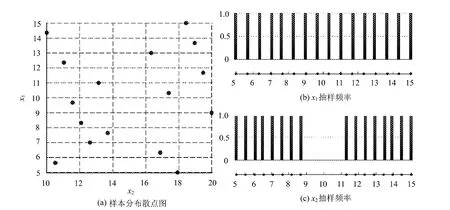
图3 分阶段抽样法样本分布散点图及变量抽样频率图
通过对比可知,两种方法都能保证不连续变量在合理取值范围内均匀抽样,但对其他连续变量的抽样,分阶段抽样法较直接抽样法均匀。
基于上述分析,采用分阶段抽样法对动臂结构进行抽样,能够有效保证教师样本分布的均匀性。
3 结构应力特征区域确定
结构应力特征区域局部最大应力值构成动臂结构应力分布预测神经网络的输出节点。特征区域选择合理与否决定了结构应力分布预测的可靠性。针对动臂结构应力特征区域的确定问题,引入基于蒙特卡洛模拟的特征区域查找方法。蒙特卡罗模拟是一种经典的实验模拟方法,它通过随机变量的统计试验或随机模拟求解问题的近似解。
根据拉丁超立方抽样确定的动臂结构样本,基于自动化动臂结构有限元分析策略,以GB9141-88中给定反铲工作装置静态应力试验的4种工况为计算工况,进行蒙特卡罗模拟。通过分析蒙特卡罗模拟得到的动臂应力响应样本数据可知,在4种计算工况中,随着动臂结构驱动参数不同,动臂结构应力分布也不同,但对样本总体而言,动臂结构最大应力值出现的位置具有明显的区域性。因此,将各个区域定义为动臂结构应力特征区域,通过比较各应力特征区域内局部最大应力值,可得到相应计算工况下结构应力的分布情况。对动臂结构而言,出现结构最大应力的特征区域如图4所示。
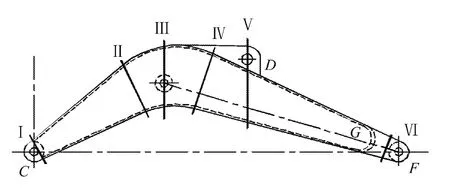
图4 动臂结构应力特征区域分布
其中,应力特征区域共有6个,各应力特征区域的位置分别如下:
1)应力特征区域Ⅰ为同时过上盖板与转台铰接座焊缝处及下盖板与转台铰接座焊缝处的截面;
2)应力特征区域Ⅱ为同时过上盖板后段与中端焊缝处及下盖板后段与中端焊缝处的截面;
3)应力特征区域Ⅲ为过动臂液压缸铰接点B并垂直CF连线的截面;
4)应力特征区域Ⅳ为同时过上盖板前段与中端焊缝处及下盖板前段与中端焊缝处的截面;
5)应力特征区域Ⅴ为过斗杆液压缸铰接点D并垂直CF连线的截面;
6)应力特征区域Ⅵ为垂直于BF连线,并过该连线和前盖板交点G与斗杆铰点F中点的截面。
蒙特卡罗模拟中,6个不同工况下不同结构驱动参数的结构应力分布图如图5所示。

图5 应力分布蒙特卡罗模拟典型分布图
4 应力分布快速预测模型构建
GB9141-88中给定了反铲挖掘机工作装置静态应力试验的4种工况。在进行动臂结构应力分析时,应综合4种计算工况,找出结构最大应力及其所在位置。因此,在构建动臂结构应力分布预测神经网络模型时,应分别针对4种工况建立4个预测模型。但对4个预测模型而言,网络结构一致,只是教师样本数据不同。
基于上述应力特征区域,可构建动臂结构应力分布预测神经网络模型,如图6所示。

图6 各计算工况下动臂结构应力分布预测神经网络模型
该网络为3层BP神经网络,充分发挥BP神经网络的非线性映射能力。网络的输入层为动臂结构驱动参数。对于不同用途的预测模型,输入层节点数有所不同。一般地,输入层节点包含所有的动臂结构驱动参数。但当预测模型用于结构优化时,由于结构优化变量往往仅是结构驱动参数中的部分参数,为提高模型预测精度,输入层节点数仅包含优化变量,节点数少于驱动参数个数。网络输出层节点为6,分别对应6个特征应力区域的局部最大应力值。中间节点数的确定有经验取值范围,但不同的节点数,网络预测精度不同。因此,中间节点的个数由神经网络训练时,在取值范围内根据最优模型的中间节点数确定。
基于上述模型,以GB9141-88中给定的第一种计算工况为例,对某机构参数下的动臂结构应力分布预测进行建模。其中,动臂结构驱动参数共21个,即模型输入层节点数为21,输出层节点数为6。基于Matlab神经网络工具箱进行建模及优化后确定中间层节点数为15。计算工况一模型训练过程曲线如图7所示。

图7 计算工况一模型训练过程曲线
模型经过376次迭代后收敛。重新抽取20个测试样本对模型进行测试,各样本在6个应力特征区域内局部最大值预测相对误差曲线如图8所示。
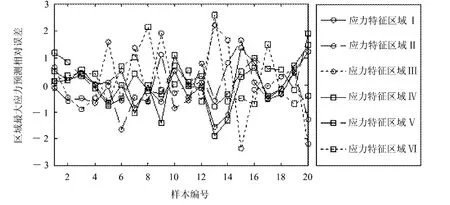
图8 预测模型训练过程精度变化曲线
最大误差<±5%,预测精度符合工程要求,且结构最大应力值所在位置预测结果与实际完全一致。从而验证了模型在预测最大应力发生位置与最大应力值的可行性和有效性。
5 结 语
1)针对现有动臂结构优化方法中存在的动臂结构应力响应求解效率低、难以求解动臂结构应力分布状态等不足,提出了基于应力特征区域的动臂结构应力分布快速预测机制,建立了结构应力分布快速预测机制框架。
2)针对动臂结构驱动参数随机组合可能出现结构畸形的问题,提出基于拉丁超立方抽样的分阶段抽样法,不仅保证了样本集中结构合理样本的数量,而且保证了样本分布的均匀性,提高了神经网络的泛化能力。
3)基于GB9141-88中给定的4种工况,通过蒙特卡罗模拟,提取了动臂结构上的6个应力特征区域,构建了某机构参数驱动下,各种工况动臂结构应力分布快速预测神经网络模型,实现了动臂结构应力分布的有效、快速预测。
[1] Mehmet Yener.Design of a computer interface for automatic finite element analysis of an excavator boom[D].Turkey:Middle East Technical University,2005.
[2] Kaung Lim,Eun-Ho Choi.An approximate optimization method for large-scaled design problem by distributed process based on the internet[C]//6th World Congresses of Structural and Multidisciplinary Optimization.[s.l.]:Riode Janeiro,2005.
[3] Perdahclolu D A,Geijselaers H J M,Ellenbroek M H M,et al.Dynamic substructuring and reanalysis methods in a surrogate-based design optimization environment[J].Structural and Multidisciplinary Optimization,2012,45:129-138.
[4] Queipo N V,Haftka R T,Shyy W,et al.Surrogate-based analysis and optimiazation[J].Aerospace Sciences,2005,41:1-28.
[5] 于兰峰,王金诺.基于遗传算法和神经网络的塔机结构动态优化设计[J].中国机械工程,2008,19(1):61-63.
[6] 文桂林,崔中,彭克立.基于近似模型的高速磨床零部件结构优化设计研究[J].中国机械工程,2009,20(8):906-910.
[7] 胡朝辉,成艾国,王国春,等.多学科优化设计在拼焊板车门轻量化中的应用[J].中国机械工程,2010,21(4):495-499.
[8] Vanderplaats G N.Structural optimization for statics,dynamics and beyond[J].Journal of the Brazilian Society of Mechanical Sciences and Engineering,2006,28(3):316-322.
[9] 黄康,张宏梅,陈科,等.人工神经网络在结构优化设计中的应用[J].机械设计,2004,21(12):18-20.
[10] 任远,白广忱.针对近似建模的前馈神经网络训练算法[J].工程设计学报,2009,16(2):122-128.
