一类拟线性抛物型偏微分方程初边值问题的逐层优化算法

张正林

（宿州学院 数学与统计学院，安徽 宿州 050000）

0 引 言

建立偏微分方程的一般步骤如下：首先要确定研究的系统和边界，从所研究的系统中划出一小微元，确定自变量与因变量；根据物理规律分析邻近部分和这个微元部分的相互作用，抓住主要因素，略去非主要因素，应用守恒定律用算式表达出这种相互作用在一个短时间里如何影响物理量；经简化整理得到偏微分方程。因为无论是初始条件中的数据，还是边界条件中的数据，甚至方程中的非齐次项，都是由实验测得，必定存在误差，如果该微小误差带来解的很大变化，这个定解问题已经没有多大的实际意义。如果给出矛盾的定解条件，解显然是不存在的。在数学上认为由实际工程问题导出的定解问题存在唯一且稳定的解，此定解问题是适定的［1］。分离变量法是求解偏微分方程常用的基本方法之一，该法将偏微分方程分离变量后化为求解含参变量常微分方程的边值问题。通常是要求出参数的值，使常微分方程边值问题对于所求出的参数值有非零解，这就是本征值问题。本征值问题是分离变量法求解数学物理方程的核心［2－7］。

1 一类拟线性抛物型偏微分方程的初边值问题

当判别式Δ＝B2－4AC＞0时，从方程（1）可以求得两个实函数解

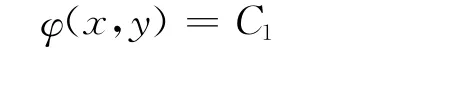
及

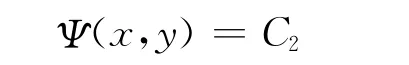
也就是说，偏微分方程（1）有两条实的特征线，于是，令

做变换并代入原方程原偏微分方程变为：

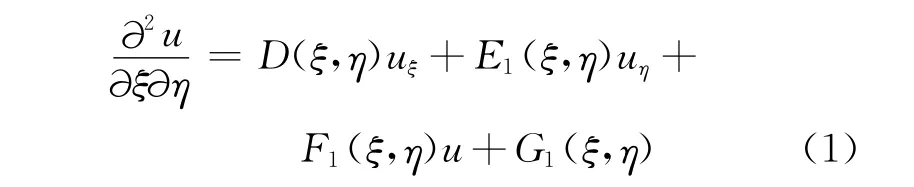
此方程称为双曲线偏微分方程的第1种标准形式，或者进一步作变换α＝ξ＋η，β＝ξ－η，偏微分方程变为：

此方程称为双曲型偏微分方程的第2种标准形式

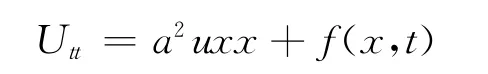
波动方程即为双曲型偏微分方程。

原方程为

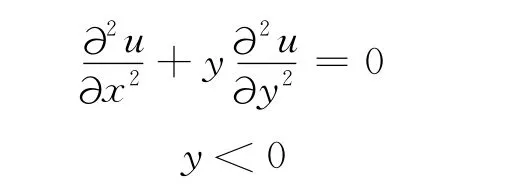
在y＜0的区域中，其判别式Δ＝B2－4AC＝0－4y＞0，所以方程为双曲型。

其特征方程为

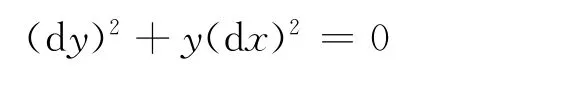
即

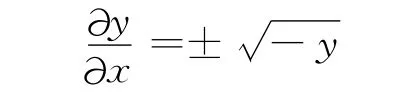
该微分方程的解为

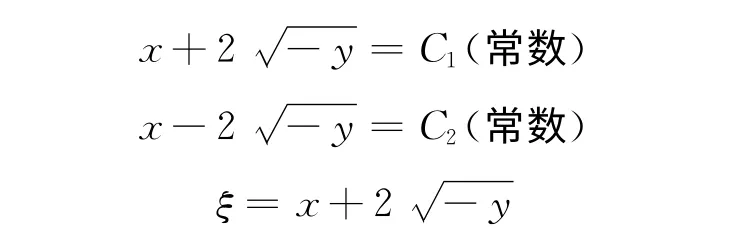
代入原方程得

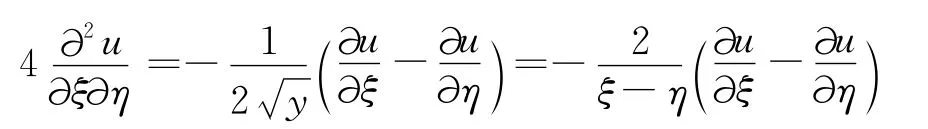
所以原偏微分方程化简为下列标准形式：

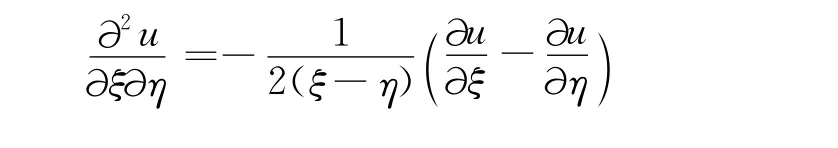
2 一类拟线性抛物型偏微分方程初边值问题的逐层优化算法

在周期性外源引起的输运问题或周期性外力作用下的振动问题，经过很多周期以后，初始条件引起的自由输运或自由振动衰减到可忽略。这时的输运或振动完全是周期性外源或外力引起。处理这类问题时，完全可忽略初始条件的影响。这类问题称为没有初始条件的问题。如在输运问题里，如果区域周围的温度或浓度是稳定的，那么经过较长时间后，区域内的温度或浓度会趋于稳定，不要误解为温度或浓度是均匀的，而是问题与时间变量无关“u≠u（t）”。这时输运方程可简化为拉普拉斯方程，没有初始条件的问题［8－10］。

试将方程

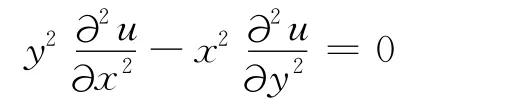
化为标准方程。

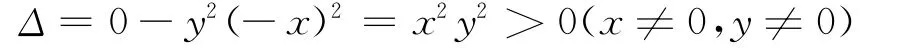
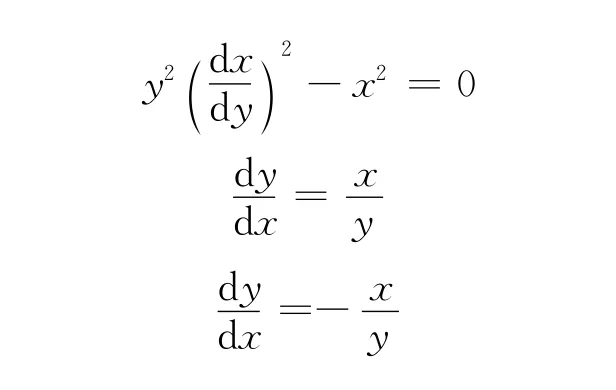
积分，得到两组积分曲线

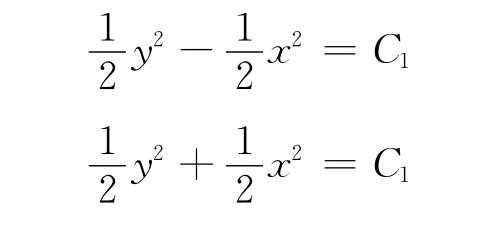
做变换

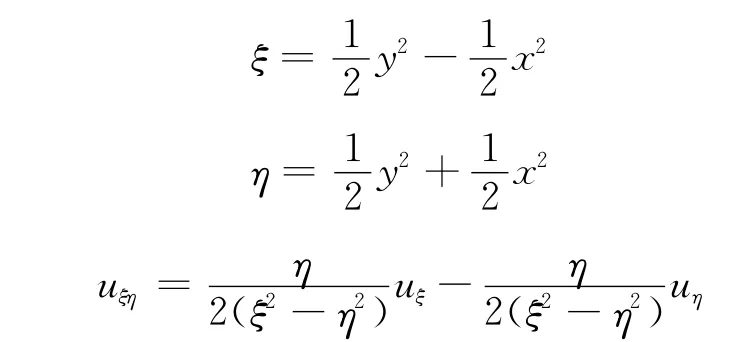
抛物型偏微分方程。

当判别式Δ＝B2－4AC＝0时，方程（2）一定有重根，所以特征曲线是一族实函数曲线。其特征方程的解为

因此令ξ＝φ（x，y），η＝y作变换，则原方程变为

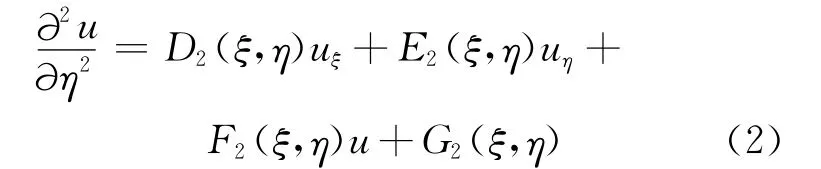
此方程称为抛物型偏微分方程的标准形式。

抛物型方程又可记为

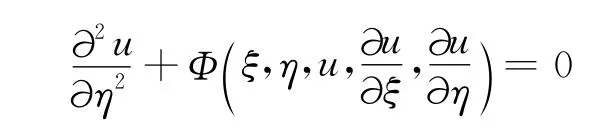
原偏微分方程为

其判别式Δ＝B2－4AC＝4x2y2－4x2y2＝0，所以特征方程为抛物型，其特征方程为

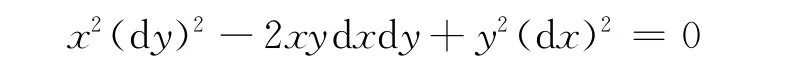
上式又可变形为

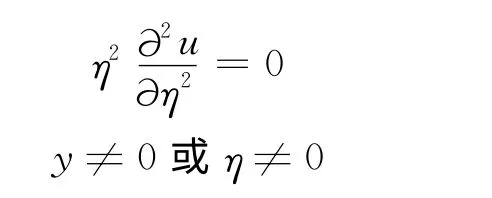
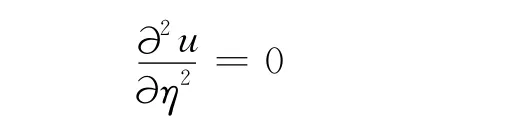
分离变量法正是利用了驻波的一个特点。既然每个特解都是满足泛定方程和边界条件的，那么一开始就可以把特解分离变量的因式之积代入泛定的方程，结合边界条件确定它们的函数形式，然后叠加成为一般解。由此产生了分离变量法。分离变量法求解偏微分方程的步骤大致分为4步：

1）把待求的特解命为变量分离的因式之和代入齐次泛定方程。把求解的偏微分方程分解为几个常微分方程；

2）关于空间坐标的常微分方程与齐次边界条件构成本征值问题，解此本征值问题，确定本征值和相应的本征函数；

3）再求解其余常微分方程的解，与本征函数相乘，找到满足边界条件的特解，将所有特解叠加成为一般解；

4）最后使用初始条件或边值条件由傅里叶级数确定一般解的叠加系数，从而得到定解问题的解。

［1］ 马亮亮，刘冬兵.高维非齐次时间分数阶电报方程的基本解［J］.四川师范大学学报：自然科学版，2015（1）：77－83.

［2］ 张媛媛，王宏伟.具扰动阻尼项波动方程的整体吸引子［J］.重庆师范大学学报：自然科学版，2015（2）：68－71.

［3］ 范乐乐，钟华.一类非线性延迟抛物偏微分方程的紧致差分格式［J］.数学的实践与认识，2015（3）：206－213.

［4］ 刘文斌，刘冬兵.高维非齐次时间分数阶扩散－波动方程的解析解问题［J］.数学的实践与认识，2015（4）：227－231.

［5］ 张媛媛，王宏伟.具耗散项非线性发展方程整体解的存在唯一性［J］.江西师范大学学报：自然科学版，2014（1）：51－53.

［6］ 赵清海，陈潇凯，林逸.基于扩散张量偏微分方程的拓扑优化过滤方法［J］.中国机械工程，2013，22：3057－3061.

［7］ 曲娜，化存才.一类非线性耦合Burgers方程组的一种差分格式［J］.高等学校计算数学学报，2013（3）：263－272.

［8］ Gennadii A Bocharov，Fathalla A Rihan.Numerical modelling in biosciences using delay differential equations［J］.Journal of Computational and Applied Mathematics，2012（1）：134－138.

［9］ W H Enright，Min Hu.Continuous Runge－Kutta methods for neutral volterra integro－differential equations with delay［J］.Applied Numerical Mathematics，2013（2）：321－330.

［10］ Desmond J Higham，Tasneem Sardar.Existence and stability of fixed points for a discretised nonlinear reaction－diffusion equation with delay［J］.Applied Numerical Mathematics，2013（1）：234－239.