基于PFM改进模型对中国非上市银行的信用风险评估

陈俐伶等

[摘要]在介绍基本的PFM模型的基础上，根据中国的实际情况对模型进行调整和完善，并选择深、沪上市的商业银行和11家非上市银行作为研究对象，基于2013年样本银行的财务数据和股票交易数据，检验和实证该模型在中国非上市银行信用风险的适用性。实证结果表明改进的PFM模型对中国非上市银行的信用评估具有一定的预测能力。

[关键词]PFM；信用风险；非上市银行

[DOI]1013939/jcnkizgsc201529211

银行业稳定性一直备受关注，自从次贷危机以来，国外金融机构陆续倒闭和破产，仅银行破产的数量就达到了将近829家。伴随着中国银行破产法相关法规的即将出台，我国众多中小型银行破产的可能性不可否认，一旦发生经营危机，就可能陷入倒闭的深渊。最近几年，国内外已经在信用风险研究上取得了大量成果。在此大背景下，我国现面临的紧要任务就是建立适于我国中小银行的信用风险评价模型。

大量实证研究表明，KMV模型是当前国内外学术界和实业界公认的信用风险度量模型之一，尤其适用于金融类和银行违约风险监测类，但其信用风险评级主要针对上市公司 。1999年KMV公司基于KMV模型和大量各行业上市公司数据库的基础上开发出适用于非上市公司信用风险度量的模型PFM（Private Firm Model），并之后公布了该模型的部分技术信息。通过大量对PFM模型的实证研究，其在欧洲和北美地区具有较强的预测能力。

国内关于使用PFM模型进行有效的信用风险评估很少需要完善。其中一些学者研究表明，与其他只以企业账面信息为基础数据的信用风险度量模型相比，PFM模型具有一定的优越性，但其在中国的预测准确率较低，对我国金融机构的信贷决策仅具有指导意义。

本文研究的目的就是探索适用于我国中小银行违约风险评估的技术，特别是针对非上市的中小银行。近些年，适用于这类企业的信用评估研究很少，本文在PFM模型的基础上，采用随机效应历史数据拟合方法进行修改和完善，利用深沪上市的商业银行和11家非上市银行作为研究对象，使用2013年样本银行的财务数据和股票交易数据，计算中国非上市银行的违约概率，并用检测曲线对其评估进行验证。

1PFM模型介绍

PFM模型是在KMV模型计算上市公司违约距离的基础上重新开发出来的一种运用于非上市公司的模型。在KMV模型中，公司违约看作公司资产价值驱动的事件过程——即公司资产价值的波动性会在一定程度上影响到公司的违约风险，这二者之间是相关联的，其中心思想很简单：企业只有当其债务高于整体的资产价值时才会发生违约事件（见图1）。

图1KMV模型思想

1.1PFM模型

对非上市公司来说，因其并不具有公开上市的股票或者债券，模型计量所需的关键数据就难以获得，不能直接得到估算。PFM模型指出，同地区、同行业、同规模的非上市公司的资产市场价值及资产价值波动率的变化和与其类似的上市公司的这一变化具有强烈的相关性。在操作中，可以根据非上市公司的情况，找出资料库中同一地区、行业具有相近EBITDA（Earnings Before Interest，Tax，Depreciation and Amortization）的所有上市公司，用中位数法取其资产市场价值作为非上市公司资产的市场价值。由此，我们可以通过与样本非上市公司各方面相似的上市公司的股权价值和其财务报表中的部分数据来估算非上市公司违约概率所需的关键变量。

PFM模型计算步骤主要分为三步：第一，估计资产价值和资产价值波动率；第二，计算违约距离；第三，计算违约概率。主要参数计算如下：

（1）估计非上市公司资产价值VA和资产价值波动率σA

第一步，用KMV模型计算公式计算上市公司资产价值（VA）、资产价值波动率（σA）。其关系采用布莱克—斯克尔斯期权定价模型定义，即：

VE=f（VA，σA，L，r，t）=VAN（d1）-Le-rtN（d2）（1）

其中：

d1=[SX（]ln（VA/Le-/rt）+[SX（]1[]2[SX）]σ2At[]σA[KF（]t[KF）][SX）]d2=d1-σA[KF（]t[KF）]

式中，VE为公司股票的市场价值；L为公司负债的账面价值；VA为公司资产市場价值；t为债务期限；σA为资产收益标准差；r为无风险利率；N（x）为标准正态分布函数。

资产的波动性与公司股票的波动性存在如下关系：

σE=ηE，AσA=（VA/VE）ΔσA（2）

其中ηE，A表示为股票价值对公司资产的弹性；△为期权的避险比率，也就是N（d2），所以

σE=g（VA，σA，L，r，t）=[SX（]N（d1）VAσA[]VE[SX）]（3）

因此，结合1.1和1.3两个方程可以求解上市公司资产的市场价值VA和资产价值的波动率σA。

第二步，以中位数对比法估计非上市公司VA、σA。首先以行业类别分组上市公司，通过计算非上市公司的PR和S，找出与该值相近的数家同行业的上市公司。再进行排序，将中位数所对应的上市公司的资产市值和资产波动率作为非上市公司的VA、σA。

（2）估计非上市公司的违约距离（DD）

违约距离是度量信用违约风险的指标，它代表着位于资产价值分布概率均值点与发生违约临界点间的距离。其表示为在T时刻公司资产市场价值到违约临界点的距离，并由将来预期资产价值收益的标准差进行调整，它可以表述为如下形式：

DD=[SX（]E[JB（[]VT[JB）]]-L[]σAT[SX）]=[SX（]V0eμT-L[]V0σA[KF（]t[KF）][SX）]（4）

从公式看出，其关键在于估计非上市公司违约点。违约距离不是一个标准化的测度方法，无法用于不同公司间的对比。因此需要引入预期违约概率来评估公司的信用状况。

（3）估计非上市公司的预期违约率EDF

在Merton模型的基本假设中仅对此做了假定，即公司资产价值波动动态过程符合对数正态分布。这样一来，此假设是否存在合理性本身就存在疑虑。出于对此的考究，主要采用了由历史数据估计得出具有统计意义预期违约概率的创新方法。其中统计意义预期违约率是基于统计方法得出的结果，被称为统计意义预期违约频率。即：

EDF=[SX（]初始时违约距离存在两个标准偏差而一年后确实发生违约的公司数量[]初始时违约距离存在两个标准偏差的公司总数[SX）]

1.2模型修正

PFM模型在国际上认为是有效的信用风险计量技术，但由于技术保密措施，具体计算方法并未得到完全公布。PFM模型以西方成熟的资本市场信用风险记录数据库为基础构建而成的，其适用性和完善性明显与我国宏观经济环境有一定出入。所以，本文结合国内外信用风险学术领域的研究成果并充分考虑我国特殊的国情，对PFM模型做出了改进和修正。

1.2.1非上市公司违约点的确定

经研究发现公司负债总额和流动负债之间必有某一点是公司的信用违约点，并且这个值的变动对计算预测的准确性影响很大。本文对于违约点的研究需要保证其适应中国股票市场的整体环境，以及能够最大化适应本文研究对象的特点，并且能够最大程度地提高模型预测能力。

本文根据中小银行数据特征，其违约点符合线性特征，表示如下：

DP=STD+ω×LTD（5）

其中ω为0到1之间某个数。STD为短期负债，LTD为长期负债。

对不同行业的研究对象来说最优的ω的取值是不同的。基于本文以中小非上市银行为主要研究对象，结合李金婷实证研究中国商业银行处于成长期特点相适应的违约点的选取方法，得出最大化适应中小非上市银行的违约点值。大量实验研究表明，行业银行ω应该选取025。该值应用于中国商业银行比KMV公司推荐设定的05得出的预测结果更加准确。由此得到的违约点在计算违约距离结果中更加客观的区分出商业银行各自的信用水平。

1.2.2估计非上市公司的VA、σA方法

基本PFM模型的中位數对比法的使用前提是假设公司财务报表相关指标与公司资产价值及其波动率之间具有较强的线性关系，实际上这种运算方法仅遵循粗略且简略的对应关系，特别是针对选取规模大小和获利能力相似的上市公司，该办法过于随意。同时鉴于我国上市银行业数量较少，中位数对比法很难实现。

因此，为了能精确的计算非上市公司的VA、σA，需要建立回归模型从而对上市公司样本数据进行统计计量分析。本文将建立资产价值与PR面板数据、账面总资产之间的回归模型，通过将相应的财务指标参数带入，通过拟合回归得出非上市银行的VA、σA。由于PR数据集不但能扩大样本银行数据容量使得回归结果更加准确有效，而且其含有具有时间序列的数据特征特别适用于研究样本总体的历史变化异动情况。本文采用的回归模型为：

VA=α1+β1（[SX（]EBITDA[]TA[SX）]）+γ1{ln（TA）}（6）

σA=α2+β2（[SX（]EBITDA[]TA[SX）]）+γ2{ln（TA）}（7）

其中，α、β、γ均为回归参数，TA为账面总资产。通过回归得到参数值，代入样本非上市中小银行对应的财务数据，估计得出其资产价值及波动率。

2基于PFM模型的实证研究

2.1样本选取

本研究的计算期为2013年全年。数据的选择对检验结果的精确程度有很大的影响。本文所需的数据主要有三大类：

第一，从wind金融数据库（上海万得资讯科技有限公司）获取的上市商业银行的证券市场数据（2013年全年股票日收盘价）和财务报表数据（营业利润，折旧，摊销，利息费用等）。样本包括工农中建交五大银行，浦发、中信等股份制银行以及北京银行等地方性银行共16家在沪、深交易所上市的国内商业银行。

第二，非上市银行的财务数据，由于我国中小银行数量大，且规模过小、机制不健全等原因导致财务信息披露不完全，数据的获取较为困难。同时得到的评估结果需要对比，所以选取非上市银行的前提是其之前得到过其他评级机构的评级。此数据主要来自样本非上市银行的年报中披露的财务报表等，具体数据见表1。

2.2参数设定

为了更好地进行信用评估研究并对其结果进行分析，我们假设研究过程中所引用的上市银行和非上市银行的财务报表准确、真实、可信。

2.2.1上市银行股权价值波动率估计

本文采用广义自回归条件方差模型——（GARCH），从历史数据中估计股权价值波动率。GARCH是一种时间序列建模技术，其运用在资产利润等经济理论中被证明是具有显著的适用性。因此，GARCH模型在金融领域运用十分广泛。通过前人大量研究得出的结论，GARCH（1.1）模型在我国股市的效果最为显著，最符合我国证券市场的特点。

GARCH（1.1）模型表达式为：

yt=C+εt（8）

σ2t=K+G1σ2t-1+A1ε2t-1（K>0，G1，A1≥0）（9）

其中，G1和A1分别代表滞后系数以及回报系数。在实际操作中，可以通过MATLAB中的GARCH工具箱得出相关参数，从而得到股权价值日收益波动率。股票日收益波动率与年收益波动率的关系为：σE=σn×[KF（]N[KF）]，其中N表示一年中的交易天数，2013年的交易天数为N=238。

对16家上市商业银行2013年全年股票日收盘价进行数据处理，得到样本上市银行股票日收益波动率和年收益波动率，见表3。由于股票收益波动率时间序列稳定性较好，所以我们用股票收益波动率来表示股价波动率。

2.2.2上市银行股权价值估计

本文16家样本上市银行均完成股权分置改革，即股权价值=基准日收盘价×总股本。由此得出上市银行在基准日（2013年12月31日）的股权价值在表3中列出。

2.2.3上市银行的资产价值VA和资产价值波动率σA

为了使运算更方便，假定计算违约距离的时间为t=1。无风险利率采用中国人民银行发布的2013年定期整存整取（年）存款利率，即r=3.50%。

本文在MATLAB中对方程组（1.1）和（1.3）进行求解，主要采用Newton-Raphson技术给出初值进行连续迭代方式求解。此种方法最大的好处是能使计算值控制在有效误差范围内。表4是运算获得的VA、σA的描述性统计。图2是当迭代次数为20时，运算获得的估计值与实际值的相对误差图。由图可以看出其中大部分银行的相对误差很小，因此采用该技术可获得相对准确的资产价值及波动率。

2.2.4非上市中小银行的资产价值VA和资产价值波动率σA的估计

根据模型修正的方法，在MATLAB中主要对方程组1.6和1.7采用随机效应最小二乘法进行拟合回归。然后根据拟合回归得到的参数和表达式，代入非上市银行2013年相关财务数据，可得到非上市银行资产价值和资产价值波动率结果见表5。

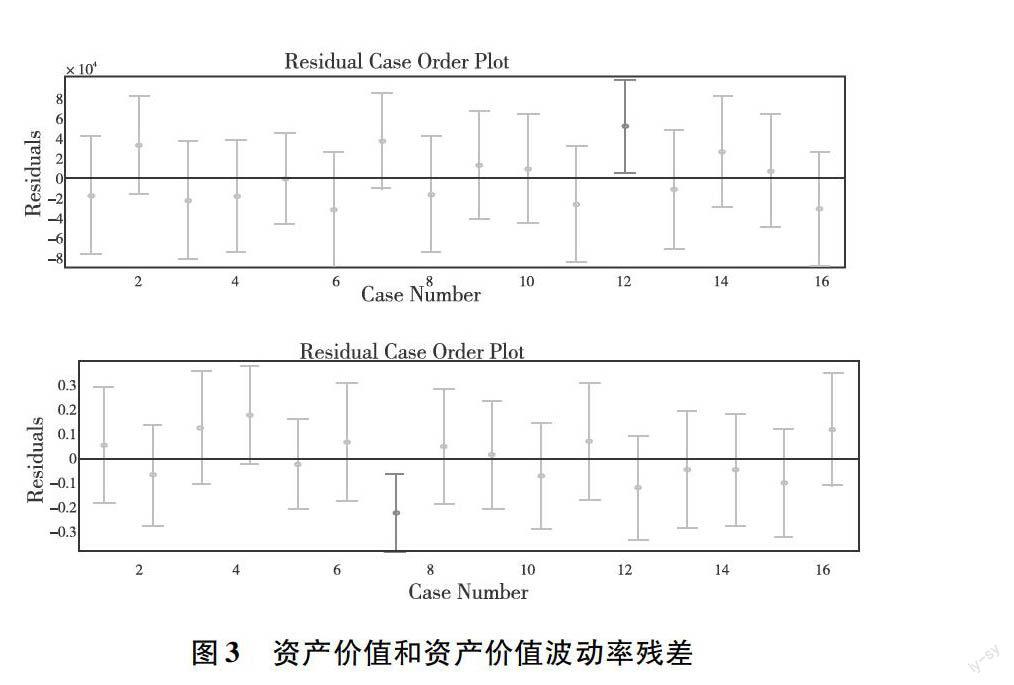
对最小二乘拟合进行拟合优度计算，图3分别表示资产价值和资产价值波动率的残差图。从图可以看出拟合模型总体表现良好，总体拟合优度>09，则拟合程度比较高。说明上市公司的总资产和EBITDA能很好地反映其资产的市场价值。

2.2.5非上市公司违约点确定

根据之前模型修正的公式（1.6）计算得出的违约点结果如表6所示。

2.2.6违约距离DD以及预期违约概率EDF的计算

假定银行未来一段时间的资产不会得到扩张，其资产增值为0，则违约距离和违约概率可以表示成：

DD=[SX（]VA-L[]VAσA[SX）]EDF=[1-N（DD）]×100%

从而计算得出预期违约距离DD和违约概率EDF如表7所示。

2.3结果验证

标准普尔（S&P）是国际上最权威的评级机构之一，其风险评级标准参照了违约概率。根据相应映射关系，我们将改进PFM模型求得的非上市银行的EDF与PFM模型和中诚信国际给出的依据S&P信用等级对应的非上市银行相应评级，其对比见图4。

通过以上数据对比，我们可以看出相比于基本PFM模型，改进后的PFM模型得出的EDF評级结果能较好地反应样本银行的信用等级。当然，免不了部分银行的信用评级仍然存在一定的误差。其主要原因中诚信国际信用评级在银行信用评级方面衡量了银行获得外部支持下的还款能力，这涉及银行所在地区以及各银行自身的外部资源，与银行的背景有很大的关系。尽管如此，这一结果仍能在一定程度上表明改进后的PFM模型对我国非上市商业银行评级适用性，对我国中小银行的信用评级有很大的指导作用。

3结论

本文在基本PFM模型的基础上加以修正和完善，利用wind数据库所获得的内地上市16家商业银行在2013年全年的股价信息以及样本银行的财务报表数据，采用MATLAB 进行运算得出具有代表性的非上市银行的违约概率，并与标准普尔评级进行对比，从而论证得出改进后的PFM模型对我国非上市银行的信用评级有一定的适用性。

当然，虽然PFM模型的修正和计量方法还有很多不完善的地方，但是该模型在中国的预测准确性不高的原因主要还有以下四点：第一，中国缺乏关于商业银行信用风险记录的大型数据库，这就限制了对本文对非上市银行信用风险估计的应用及验证，同时也是中国信用风险研究比较落后的原因之一；第二，中国股市出于规范和发展阶段，股价对上市公司的信息反映不充分，非理性和主观操纵的因素较多，导致股票市场有效性不强；第三，PFM模型中的关键计算步骤以及计算方法并不完全公开，其主要由于提出该基本模型的公司是以盈利为目的，因此在未来的学术研究上需加强对其中参数的关键计算公式和细节进行进一步的研究和拓展；第四，最后由于我国对中小非上市银行进行评级的国际大型评级机构很少，所以进行评估选用的仅仅是中诚信国际发布的2013年样本非上市银行的评级报告，缺乏权威性和实际可对比性。综上所述，本文研究主要目的则是希望中国对中小银行甚至中小非上市企业的信用状况进行重视，同时也为此类企业的评级提供借鉴的思路。

参考文献：

[1]Lee WCRedefinition of The KMV Models Optimal Default Point Based on Genetic Algorithms——Evidence from Taiwan[J].Expert Systems with Applications，2011，38（8）：10107-10113.

[2]彭大衡，张聪宇银行信用风险演变的KMV模型分析——以五家中小商业银行为例[J].经济数学，2009（3）：60-69

[3]Lin L，Lou T，Zhan NEmpirical Study on Credit Risk of Our Listed Company Based on KMV Model[J].Applied Mathematics，2014，5（13）：2098

[4]张泽京，陈晓红，王傅强基于 KMV 模型的我国中小上市公司信用风险研究[J].财经研究，2007，33（11）：31-40

[5]Nyberg M，Sellers M，Zhang JPrivate Firm Model-Introduction to the Modeling Methodology[J].KMV LLC，2001.

[6]戴志锋，张宗益，陈银忠基于期权定价理论的中国非上市公司信用风险度量研究[J].管理科学，2006，18（6）：72-77

[7]Crosbie P，Bohn JModeling Default Risk[J].2003.

[8]应千凡中国非上市公司信用风险度量研究[D].杭州：浙江大学，2007

[9]李金婷上市商业银行信用风险评价中违约点设定公式研究——以招商，浦发，华夏，民生，深发展为例[J].中国新技术新产品，2009（1）

[10]周杰修正的 KMV 模型在上市公司信用风险度量中的应用分析[J].财会通讯：综合（下），2009（5）：8-10

[11]鲁炜，赵恒珩，刘冀云KMV 模型关系函数推测及其在中国股市的验证[J].运筹与管理，2003，12（3）：43-48

[12]罗光熹，周安，王艳花应用Newton-Raphson法计算水化物生成温度[J].天然气工业，1989，9（2）：63-67