一种提高傅立叶算法分辨率和精度的方法研究*

2015-06-11陈钊，符娆，雷利

机械研究与应用 2015年2期

陈钊，符娆，雷利

(中国飞行试验研究院，陕西西安 710089)

0 引言

在传统的傅立叶变换算法中，选取的分析数据长度和频率分辨率有直接关系，而在实际工程应用中，如果选取的分析数据长度过短，则频率分辨率过低，而且可能导致计算的幅值小于真实值，产生较大的误差，如果选取分析数据长度较长，会提高分辨率，但会引发新的问题，在该段数据内，信号的频率不一定是稳定的，依然会导致计算结果误差过大［1］，提高分辨率还有一种常用的做法是补零，该方法也可以有效的提高频率分辨率，但是该方法不能提高计算精度［2］。

笔者针对这个问题，提出了一种改良的傅立叶算法，在不增加分析数据长度的同时，提高算法的分辨率和精度。

1 算法原理

对于任何一个函数f(t)，展开成三角形式的傅立叶级数为:

根据三角函数的正交性，公式(1)中的个性系数如下［3］:

笔者对公式(1)进行改良，增加一个新的参数m，新的傅立叶算法公式为:

根据三角函数的正交性，公式(2)中的个性系数如下:

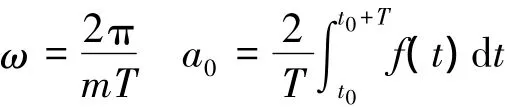
2 仿真计算

现产生一组仿真振动信号为:

如果分析数据点数 N和采样率 fs一样，均取8192，那么分辨率即为1 Hz，采用传统的傅立叶方法进行分析，得到频谱图如图1所示。

图1 传统傅立叶算法对仿真数据分析结果

信号存在160.5 Hz和360 Hz两个频率，傅立叶分析时，由于160.5 Hz处在分辨率所在的160 Hz和161 Hz之间，其分析结果与实际值产生了非常大的误差，信号实际幅值为10，而分析结果仅为6.356，只有实际值的63.56%，误差高达36.44%，这个误差已经超出了大部分工程分析的可接受范围，而360 Hz恰好在分辨率所在频率上，计算结果与实际幅值非常接近，误差仅为0.44%。

而在实际工程中，振动信号的频率很难恰好出现在分辨率所在频率上，因此必须提高分析精度，才可以得到更加准确的振动幅值。传统的分析方法中，提高分辨率的方法是增加分析数据长度，而增加数据长度则可能带来很多新的问题。

现采用改良后的傅立叶分析方法对仿真信号进行分析，取m=0.1，即将分辨率提高10倍，由原来的1 Hz提高到0.1 Hz，分析结果如图2所示。

从图2的分析结果可以看出，改良后的傅立叶算法在360 Hz频率的分析结果与传统的傅立叶分析结果一致，而在160.5 Hz的频率，改良后的傅立叶算法分析结果幅值为 10.01，与真实结果 10只误差了0.1%，精度得到了很大的提升。

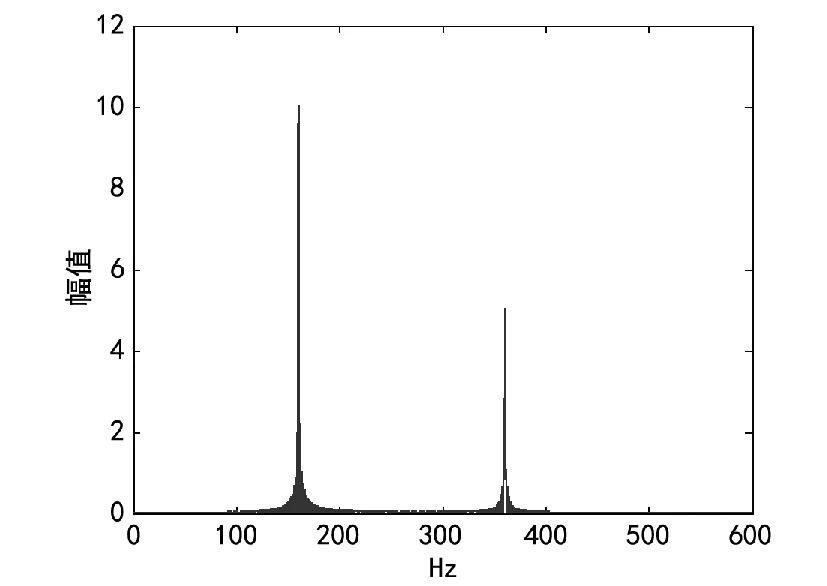
图2 改良傅立叶算法对仿真数据分析结果

3 对航空发动机实际振动数据进行分析

在某型发动机试飞过程中，曾经发生发动机空中停车故障，现提取该发动机空中停车期间的振动数据，分别采用传统傅立叶法分析和改良后的傅立叶算法对该数据进行分析，如图3、4所示。

图3 传统傅立叶法分析结果

图4 改良后傅立叶法分析结果

该数据采样率为12 500，每次分析数据长度为8192，即分辨率为1.35 Hz，改良后的傅立叶法分析分辨率为0.1 Hz。两种方法分析结果对比可以发现，不管采用传统的方法还是改良后的傅立叶法，计算出来的燃发器振动幅值和动力涡轮振幅幅值的变化规律都是一致的，但是两种方法计算出来的幅值大小有一定的区别，具体差别如表1所列。

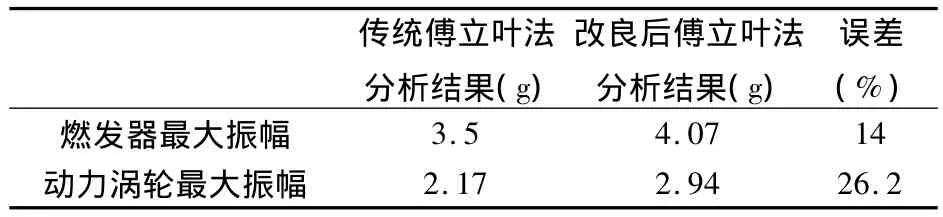
表1 两种分析方法对比结果

从表2的对比结果可以看出，两种方法的计算结果存在很大的差别，改良后的傅立叶法分析结果都比传统的傅立叶法分析结果大，根据仿真计算的经验，传统傅立叶法的分析结果在很多时候都可能降低振动的幅值，使处理结果小于真实振动幅值，因此认为改良后的傅立叶法分析结果更为可信，在整个发动机空中停车的过程中，燃发器最大振动幅值应为4.07 g，动力涡轮的最大振幅为2.94 g。

4 改进后的傅立叶法存在问题和解决方法

改进后的傅立叶法可以很大程度上提高数据处理精度，但是会产生很大的运算量，如果取m=0.1，运算量会是传统傅立叶算法的10倍，在工程上会存在很多问题，笔者提出一个解决方法，具体流程如图5所示。

如对仿真信号的分析，可首先采用传统的傅立叶算法进行分析，根据传统的傅立叶算法结果，可以确定振动信号的频率在160 Hz和360 Hz左右，而后可选取158 ～162 Hz，358 ～362 Hz，这两个区间段采用改良后的傅立叶法进行分析，分别取0.1 Hz。采用这种方法，既可以准确的得到振幅幅值，又不产生较大的运算量。