浅谈检测分析质量控制中的精密度问题

2015-06-11王秀萍刘发现王淑华马春香刘春榉

化工科技 2015年5期

王秀萍，刘发现，杨帆，王淑华，马春香，刘春榉

(1.中国石油吉林石化公司研究院，吉林吉林 132021；2.中国石油吉林石化公司合成树脂厂，吉林吉林 132022；3.中国石油吉林石化公司，吉林吉林 132022；4.中国石油吉林石化公司炼油厂，吉林吉林 132022；5.天津灯塔涂料有限公司，天津 300400)

质量控制是实验室确保检测结果准确的一个重要环节，在实验室资质认定评审准则和实验室认可准则中都突出强调了结果质量控制的问题，而且指出了质量控制的方法，如定期使用有证标准物质、实验室间的比对、使用相同或不同方法进行重复检测和对存留样品进行再检测[1-2]等。这些方法如何运用，运用过程中精密度的问题应如何考虑，准则中并未给出明确的指导，因而在实验室质量控制活动中有可能偏颇，可能存在着只考察结果的准确度或可比性而忽略了对精密度的要求。作者对标准物质验证和2个结果比对中精密度的问题重点加以阐述。

1 一组数据精密度的可接受性判定

1.1 2次平行测定结果的允差

精密度符合要求是质量控制活动中检验结果可比性以及检验结果准确性的前提。

2次平行测定结果的允差也称重复性/限，用r表示，常常在标准中给出，如标准GB/T 2441.1—2008《尿素的测定方法第1部分总氮含量》规定“平行测定结果的绝对差值不得大于0.10%[3]”，即总氮含量2次平行测定结果的允差(重复性/限)r=0.10%。r=2.83σr，σr称为室内标准偏差，因此室内标准差σr=0.10%/2.83=0.035%。

如果考察2个平行测定结果的精密度是否可接受，用标准允差衡量即可。平行测定结果的绝对差值小于等于允差，其精密度即符合要求。

1.2 n次测定值的临界极差

在质量控制活动中常常在重复性条件下测定多个数据进行统计处理。n个测试结果的临界极差[4]判定公式见式(1)。

xmax-xmin≤CR0.95(n)

(1)

CR0.95(n)=f(n)σr

(2)

xmax、xmin分别为一组测定数据中最大值和最小值，CR0.95(n)为临界极差，f(n)为临界极差系数。

n个测试结果的极差(xmax-xmin)小于等于临界极差，则表示这几个测试结果的精密度符合要求。

例如依据 GB/T 2441.1—2008测定尿素中总氮含量，同一个样品在重复性条件下测定了6次，测定结果分别为46.43%、46.36%、46.29%、46.38%、46.44%和46.36%，则6次测定结果的极差xmax-xmin=46.44%-46.29%=0.15%，σr=0.10%/2.83=0.035%，查表[4]可知f(n)=4.0，则CR0.95(6)=f(6)σr=4.0×0.035%=0.14%，xmax-xmin>CR0.95(6)，所以此组数据精密度不能满足要求。这样的一组数据不能再进一步评价其均值的准确度或可比性。

2 单次测定值的限定

2.1 标准物质验证

用有证标准物质监控检测质量(也称为标准物质验证)可以对检测过程的人、机、料、法、环等因素进行检查监控，是很好的质量控制手段。用有证标准物质监控检测质量时，按照测定样品的方法测定有证标准物质，用式(3)进行评价。

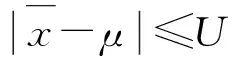
(3)

标准物质铜溶液的证书标识结果见表1。根据表1计算出绝对不确定度U=3.00 μg/mL×1%=0.03 μg/mL。

表1 原子吸收分光光度计检定用标准物质(铜溶液)

标准物质铜溶液6次测定结果见表2。

表2 测定标准物质铜溶液结果

根据式(3)计算得到

显然，测定标准物质铜溶液满足式(3)。

根据表1 的数据以及不确定度评定过程选用的置信概率可知，标准物质铜溶液中铜质量浓度量值为一范围，即3.00±0.03 μg/mL，其置信概率为95%，由此说明20次测定数据中只允许1次测定值超过此范围，而表2显示的6次数据中有1次超过3.00±0.03 μg/mL，属于小概率事件，是不应该出现的，因而示例中单次测定值不符合要求。单次测定值不符合要求，评价平均值没有意义。

如果采用式(3)评价标准物质的测定结果，单次测定值应满足 |xi-μ|≤U，其中xi为单次测定值。

2.2 2个数据比较

2个比对结果也可以用标准中规定的允差(重复性/限)作为衡量的尺度，如硬脂酸锌中锌含量的测定，标准HG/T 3667—2012 《硬脂酸锌》中规定“锌含量2次平行测定结果的允许差不大于0.30%”。假设采用2种方法测定的结果分别为4.31%和4.13%，二者结果之差为0.18%，根据标准HG/T 3667—2012允差规定可以判定，2个方法测定结果是可以接受的，因为不同方法测定结果之间的允许差一定大于0.30%。

如果仅仅考虑2个方法的一对测定值或是2个方法的平均值，上述判定结果的可接受性可能是假象，因为尽管每对单次测定值或平均值之差绝对值满足重复性要求，但若方法1的所有单次测定值都高于或低于方法2的单次测定值，2种方法之间则显然存在系统误差。为此，运用该方法评价比对结果时，2组结果的单次测定值应相互交叉，随机分布，不能是不相交的2条线。在此基础上，再考察2个结果或2组均值的可比性。