子午线轮胎固有频率和阻尼辨识的数值与实验研究*

冯希金，危银涛，朱光苗，陈亚龙

(1.清华大学 汽车工程系,北京 100084；2.青岛大学 应用技术学院,山东 青岛 266061)

轮胎是汽车与地面接触的唯一部件，汽车的NVH性能与轮胎有紧密的关系，许多学者在这方面做了大量的研究[1-6]，在这些研究中轮胎常被简化成由粘壶和弹簧组成的阻尼结构，但并没有给出轮胎阻尼辨识方法。在用来评估车辆的平顺性和舒适性的先进轮胎模型[7]如Ftire、RMODK模型时，也用到了轮胎在各阶模态下的固有频率和阻尼比等参数，因此辨识轮胎的固有频率和阻尼比是进行车辆NVH性能研究和开展轮胎振动噪声分析的一项重要工作。

轮胎是由多种橡胶和帘线组成的复合材料结构，轮胎的NVH特性受橡胶材料、帘线材料的性能影响，也受轮胎的充气压力等工作条件的影响。自从人们认识到轮胎的NVH特性的重要性后，许多学者利用实验或者解析理论模型的方法对轮胎的固有频率和阻尼特性进行了研究。Reiter等[8]在实验室内对斜交卡车胎的振动和由各阶振动带来的噪声进行了测量和研究，得到了各阶径向振动模态所对应的固有频率，考察了气压对固有频率的影响。管迪华等[9]采用模态实验方法来研究轮胎固有频率和阻尼特性，Potts等[10]采用弹性基座上的细环模型，推导出了轮胎各阶固有频率的求解公式，并与实验结果进行了对比。葛建敏等[11]开发了测量轮胎水平阻尼和垂直阻尼的实验设备，研究了阻尼随着气压和速度的变化关系，并形成了简单计算公式。Seokyong等[12]采用带简单花纹的瞬态有限元模型和刚性环模型研究了轮胎振动和阻尼特性。

上述轮胎振动和阻尼的研究多采用解析方法和实验方法，解析方法多采用刚性环模型，无法将计算结果和轮胎的真实结构直接关联起来，缺乏轮胎阻尼比解析分析和实验研究的对比。

本文采用Abaqus软件结合实验来进行卡车子午胎的振动和阻尼特性的研究，橡胶材料模型采用了超弹性模型和黏弹性模型，建立了光面胎轮胎模型，模型中还考虑了单元类型对固有频率的影响。最后采用分量法对仿真得到的频率响应函数进行处理，得到了轮胎的阻尼固有频率和各阶阻尼比。在实验室内进行了轮胎的固有频率和各阶阻尼比的实验，实验结果和仿真计算结果非常接近，证明了仿真方法的可靠性。

1 动力学问题的有限元求解方法

根据动力学系统的基本理论[13]，求解动力学响应的基本方程，见式(1)。

(1)

如果忽略阻尼的影响，并使上式的右端项为零，则式(1)进一步简化为式(2)。

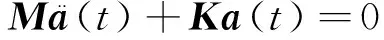
(2)

式(2)为系统的自由振动方程，由此可以求解出系统的无阻尼固有频率和模态。

2 模态参数提取的分量法

2.1 单自由度系统阻尼比求解

根据振动模态分析与参数辨识理论[14]，黏性单自由度系统频响函数的实部表达式为式(3)。

(3)

(4)

(5)

从而可以得到：

(6)

从式(6)可见，只要从实频图上得到固有频率ωr和2个极值频率ω2和ω1，就可以得到阻尼比ξ。

2.2 模态参数辨识的分量分析法

模态参数辨识的分量分析法正是利用了频响函数的的上述特点来进行参数辨识的。对一个具有N自由度的黏性阻尼系统，在p点激励，在L点测量响应，其频响函数可表示为式(7)。

(7)

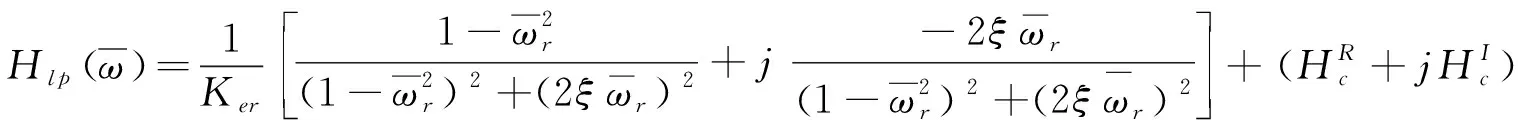
(8)

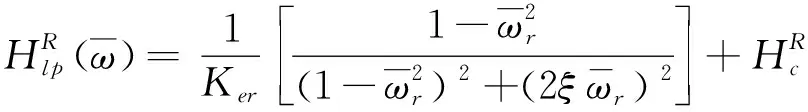
(9)

如果忽略剩余模态的影响，则式(9)与单自由度的公式类似，因此可以从实频图上读取第r阶模态的固有频率ωr以及2个极值点的频率ω1和ω2，根据式(6)计算得到各阶模态的阻尼比。

3 轮胎有限元模型的建立

3.1 光面轮胎有限元模型

图1和图2分别表示光面胎的二维有限元模型和三维有限元模型，为了保证分析结果的可靠性，网格划分比较细，二维有2 252个节点，2 094个单元，将二维模型绕轮胎轴旋转120份，得到轮胎三维模型。

图1 二维有限元模型图

图2 三维有限元模型

3.2 单元类型的选择

为了考察单元类型对固有频率的影响，在光面轮胎的有限元模型中分别采用了2种类型的单元模拟橡胶材料：减缩积分单元C3D8R和杂交单元C3D8H。对于轮胎中的带束层、胎体层、冠带层、钢丝圈等复合材料，采用Rebar单元模拟，在Abaqus中二维的Rebar单元类型是SFMGAX1，三维的Rebar单元类型是SFM3D4R。

3.3 材料参数的确定

3.3.1 橡胶的超弹性模型和超弹性材料参数的确定

硫化橡胶是一种超弹性材料，其材料本构模型种类比较多，最常用的有Mooney-Rivlin模型、Yeoh模型、Neo-Hookean模型等。由于Neo-Hookean模型的优点是只有一个材料常数，并且具有无条件稳定性，一种变形方式下的应力应变曲线拟合的材料常数能用来预测其它变形方式的应力应变曲线。根据本文研究工作的特点，选用Neo-Hookean模型，采用单轴拉伸实验数据进行曲线拟合得到材料参数。

3.3.2 橡胶的黏弹性模型和黏弹性参数的确定

橡胶材料的另一个特点是黏弹性，正是由于橡胶具有黏弹性，所以才使轮胎具有了阻尼特性，因此要进行轮胎的动态特性分析并求解其阻尼，必须考虑橡胶的黏弹性。一般采用Prony级数模型表达橡胶的黏弹性。

3.3.3 钢丝帘线的材料参数和Rebar单元参数的确定

钢丝帘线等骨架材料的材料特性用各向同性材料来模拟，带束层、胎体层、冠带层等复合材料采用代表骨架材料的Rebar单元嵌入到橡胶单元中来实现。Rebar单元的材料参数包括单根帘线截面积、帘线间距、方向角，这些参数都可以从轮胎生产工艺参数上得到。

3.4 边界条件和载荷条件

轮胎的充气压力采用标准充气压力830 kPa，轮辋采用标准轮辋。本文的分析中共有3个载荷步，第1个载荷步是给轮胎安装轮辋和充气；第2个载荷步是采用LANZCOS方法进行轮胎的无阻尼固有频率的提取；第3个载荷步是对轮胎上的某一点进行正弦激励，激励力为式(10)。

F=1 000sinwt

(10)

图3给出了激励点(A点)和响应点(B点)的位置，通过提取响应点的实频图来辨识阻尼固有频率和阻尼比。

图3 有限元仿真中的激励点和响应点

4 轮胎的模态实验

为了验证有限元仿真结果的可靠性，进行了轮胎的振动模态实验，如图4所示。给轮胎充气到标准气压830 kPa，连轮辋一起固定在轴上，采用单点激励，多点测量的方法来测试轮胎的响应，轮胎一周共布置16个测量点，测得的信号用设备自带软件进行处理，可以得到各阶固有频率、振动模态和阻尼比。

图4 轮胎的振动模态实验

5 结果与讨论

5.1 仿真得到的振动模态形状与实验得到的振动模态形状的对比

图5～图9给出了不同阶次的径向振动模态形状与实验测得的径向振动模态形状的对比，可以看出计算得到的模态形状和实验得到的形状完全一致。

图5 径向一阶振动模态示意图

图6 径向二阶振动模态示意图

图7 径向三阶振动模态示意图

图8 径向四阶振动模态示意图

图9 径向五阶振动模态示意图

5.2 阻尼固有频率、无阻尼固有频率与实测固有频率的对比

阻尼固有频率的计算以及阻尼比的计算，按照2.2所述的方法进行。根据轮胎有限元仿真的结果，输出响应点的位移响应的实频图(如图10所示)，然后根据实频图采用2.2的方法计算各阶模态的阻尼固有频率以及2个极值点的频率，从而根据式(4)来计算得到各阶模态的阻尼比。

频率/HzA、B、C、D、E为第1～5阶径向模态的正共振点，A′、B′、C′、D′、E′为第1～5阶径向模态的反共振点图10 响应点的位移响应的实频图

从表1可以看到，阻尼固有频率与实测频率相比，基本很接近，最大的误差在径向二阶固有频率，其误差不到5%。轮胎的阻尼对固有频率的影响较小，最大误差在第一阶，为0.5 Hz。

从表1还可以看到，一般无阻尼固有频率大于阻尼固有频率。但在高阶时阻尼固有频率接近甚至大于无阻尼频率。

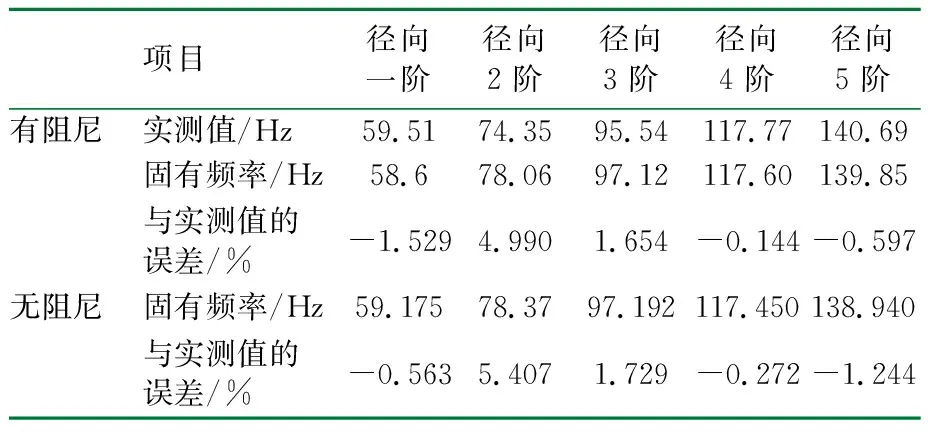
表1 阻尼固有频率、无阻尼固有频率与实测固有频率的对比

5.3 阻尼比与实测阻尼比的比较

进一步采用分量法求解其各阶阻尼比，将计算求得的阻尼比和实验测量得到的阻尼比对比，结果如表2所示。

表2 计算得到的阻尼比与实验结果的比较

从表2可见，阻尼比的计算结果和实测结果之间误差在10%左右，最大达到23.7%。低阶的阻尼比误差较小，高阶阻尼比误差较大，之所以造成这个现象，是因为高阶下响应点的位移衰减过快，从而导致从位移实频曲线来推算阻尼比有较大误差。

6 结 论

(1) 结合轮胎有限元分析和轮胎模态实验，提出了一种轮胎固有频率和阻尼比的快速可靠辨识方法，得到了比较好的频率和阻尼的辨识精度，是一种简单可行的方法。

(2) 模态分量法辨识得到的轮胎阻尼固有频率与实测结果相比误差很小，对阻尼比的辨识误差在10%左右，高阶下误差达到23.7%，因此该方法只适合求解低阶阻尼比，高阶阻尼比还需要探索其它方法。

参 考 文 献：

[1] Mavros G.A Study on the influences of tyre Lags and suspension damping on the instantaneous response of a vehicle[J].Journal of Automobile Engineering,2008,222(4):485-498.

[2] Dohrmann C R.Dynamics of a tre-weel-sspension asembly[J].Journal of Sund and Vibration,1998,210(5):627-642.

[3] HuseyinAkcay,SemihaTurkay.Influence of tire damping on actively controlled quarter-Car wuspensions[J].Journal of Vibrations and Acoustics,2011,133(5):1-6.

[4] Junghsen Lieh.Tire damping effect on ride quality of vehicles with active control suspensions[J].Journal of Vibration and Acoustics,2009,131(3):1-6.

[5] Scavuzzo R W,RichardsT R,CharekL T.Tire vibration modes and effects on vehicle ride quality[J].Tire Science and Technology,1993,21(1):23-39.

[6] Captain K M,Boghani A b,Wormley D N.Analytical tire models for dynamic vehicle simulation[J].Vehicle System Dynamics,1979,8(1):1-32.

[7] 危银涛,Michael Kaliske,黄友剑.轮胎橡胶制品先进力学[M].北京:清华大学出版社,2013:96-132.

[8] Reiter W F,Jr.Resonant sound and vibration characteristics of a truck tire[J].Tire Science and Technology,1974,2(2):130-141.

[9] Dihua G,Weidong W,Aiqian Z.Tire modeling for vertical properties by using experimental modal parameters[J].SAE Paper No.980252.

[10] Potts G R,Bell C A,Charek L T,et al.Tire vibrations[J].Tire Science and Technology,1977,5(4):202-225.

[11] Jianmin G,Gall R,Zuomin W.Dynamic damping and stiffness characteristics of the rolling tire[J].Tire Science and Technology,2001,29(4):258-268.

[12] SeokyongChae,Moustafa EI-Gindy,Mukesh Trivedi,et al.Dynamic response predictions of a truck tire using detailed finite element and rigid ring models[C]//Proceedings of IMECE04,2004 ASME International Mechanical Engineering Congress and Exposition,November 13-20,2004,Anaheim,California USA.

[13] 王勖成．有限单元法[M]．北京:清华大学出版社，2003：468-520．

[14] 傅志方.振动模态分析与参数辨识[M]．北京：机械工业出版社，1990：132-136.