T形截面三维编织复合材料细观结构分析及弯曲性能预测
2015-06-10于陈陈代艾波张小萍
于陈陈, 瞿 畅, 邓 婕, 代艾波, 张小萍
(南通大学 机械工程学院, 江苏 南通 226019)
T形截面三维编织复合材料细观结构分析及弯曲性能预测
于陈陈, 瞿 畅, 邓 婕, 代艾波, 张小萍
(南通大学 机械工程学院, 江苏 南通 226019)
根据矩形组合截面三维编织复合材料四步法编织原理,分析了T形截面编织物的纱线运动规律;按照载纱器的水平运动规律确定了纱线的空间运动轨迹,并用控制体积法建立T形截面交接区域的特殊细观结构模型。在假设纱线截面为椭圆形等理想状态下,建立了编织工艺参数之间的数学关系。运用弯曲刚度合成法预测出T形截面三维编织复合材料的弯曲性能,用MatLab编写了弯曲模量的计算程序。结果表明:弯曲模量随编织角的增大而减小,随纤维体积含量的增加而增大,三维五向T形截面梁的弯曲性能优于三维四向的。最后将预测结果与实验结果进行比较分析,结果证实用弯曲刚度合成法预测T形截面三维编织复合材料的弯曲性能是可靠的。
三维编织; T形截面; 细观结构; 弯曲性能
三维编织复合材料具有良好的整体性能、合理的力学结构及较高冲击和断裂容限扩张能力,其应用日益广泛[1]。研究三维编织复合材料的力学性能,可为其设计制造及应用提供理论参考。实际工程应用中,许多复合材料制件常常在弯曲载荷下工作,研究复合材料的弯曲性能显得尤为重要[2]。目前,在三维编织复合材料弯曲性能预测及实验研究方面已取得一些研究成果。如陈利等[3]基于经典层合板理论,提出了三维四向编织复合材料弯曲性能的一种预测方法;王波等[4-5]分别采用三点弯曲和四点弯曲试验测试了三维四向编织复合材料的弯曲性能,并运用刚度合成法预测裁剪所得的三维四向编织复合材料的弯曲模量;李典森等[6]采用改进的刚度平均化方法,对三维多向编织复合材料的各单胞及各层的弹性性能进行预测与分析,并推导出材料的弯曲模量;Zhang等[7-8]利用声发射技术对L形和矩形截面三维编织复合材料的弯曲性能进行了比较,并分析了交接区域细观结构对弯曲性能的影响;陈光伟等[9]以三维编织复合材料T形截面梁为研究对象,对其抗弯性能进行了数值模拟,分析了纤维束的交织结构和细观结构参数对T形截面梁抗弯性能的影响;董纪伟等[10]从基于小参数渐进展开的多尺度均匀化理论出发,对三点弯曲作用下3种单胞内应力分布进行了数值模拟。Zhao等[11-12]对四步法三维编织复合材料矩形梁不同应力水平下的弯曲疲劳性能进行实验研究,并对其弯曲疲劳性能进行了有限元分析。张中伟等[13]对三维编织复合材料 T 型梁进行准静态三点弯曲测试,得出了筋高处纤维的断裂是导致材料最终失效的主要破坏模式的结论。
上述这些研究主要集中在矩形截面的编织复合材料,实际工程应用中,工字梁、口字梁、T型梁等矩形组合截面三维编织复合材料是工程使用中承受弯曲载荷的重要结构件,研究矩形组合截面三维编织复合材料的弯曲性能对工程材料的高效、安全使用具有指导意义。本文以T形截面三维编织复合材料为例,建立了矩形交接区域的特殊细观模型,并采用弯曲刚度合成法预测了T形截面三维编织复合材料的弯曲性能,分析了编织参数对弯曲性能的影响规律。
1 T形截面三维编织物的细观结构
研究矩形组合截面三维编织复合材料的力学性能,要以矩形截面编织物的细观结构为基础。由于矩形组合截面编织物与矩形截面编织物的编织工艺不同,导致矩形组合截面编织物中存在特殊的细观结构。本文通过分析纱线在编织过程中的运动规律,运用控制体积法分析并建立了T形截面编织物的细观结构模型。
1.1 纱线的运动规律
T形截面1×1样式的编织物采用四步法编织而成,图1为三维四向T形截面编织物的排纱图。
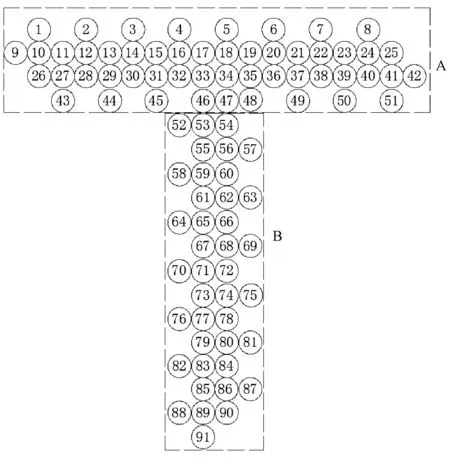
图1 三维四向T形梁排纱图Fig.1 Arrangement of yarn in 3-D 4-directional braided composites of T beam
把T形截面看作由横向矩形A和纵向矩形B组合而成,分别对2个矩形截面进行编织,1~4步编织矩形A。第1步,矩形A中不同列的纱线交替向上或向下运动一个纱线的位置;第2步,矩形A中不同行的纱线交替向左或向右运动一个纱线的位置;第3、4步分别与第1、2步的运动相反;5~8步编织矩形B;第5步,矩形B中不同列的纱线交替向上或向下运动一个纱线的位置;第6步,矩形B中不同行的纱线交替向左或向右运动一个纱线的位置,第7、8步分别与第5、6步的运动相反;一共8步完成1个编织循环,形成1个花节高度h。经过若干个编织循环后,载纱器回到最初的排纱位置。图2示出部分载纱器的运动规律,图中粗虚线边框内部为两矩形的交接区域。

图2 纱线水平运动规律Fig.2 Yarns movement in horizontal direction. (a)Movement of carrier ; (b)Movement of carrier ④; (c)Movement of carrier ; (d) Movement of carrier ; (e) Movement of carrier

1.2 交接区域的细观结构
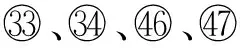
1)假设纤维束截面形状为椭圆形,短轴为d,并且沿轴线方向保持不变;
2)编织纱线在水平面的投影与预制件厚度方向的夹角为φ;
3)编织结构均匀稳定,纱线处于挤紧状态;
4)忽略编织过程中纱线产生的弯曲情况。
1.2.1 交接内部单胞
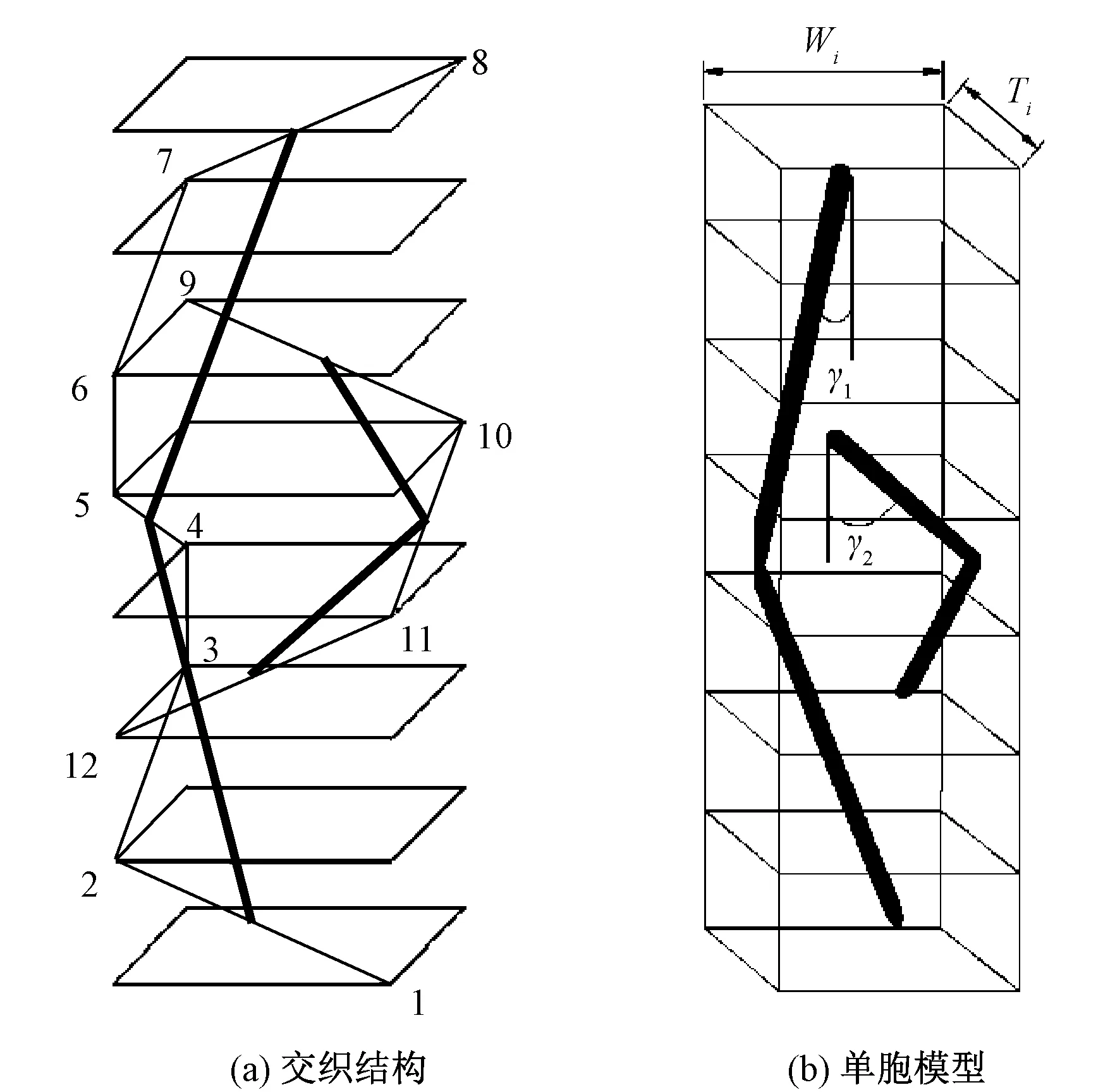
图区域交织结构和单胞模型Fig.
图3(b)示出交接区域内部单胞的单胞模型。设内部单胞的宽度和厚度分别用Wi、Ti表示,γ1、γ2为内部编织角。根据上述假设和图3中所示的几何关系,可得到以下数学关系:
(1)
1.2.2 交接角胞S
同样方法可得交接角胞S的交织结构和单胞模型,如图4所示。设单胞模型的宽度和厚度分别用Ws、Ts表示,α1、α2表示内部编织角,可得到以下数学关系:
(2)

图区域交织结构和单胞模型Fig.4 Yarn structure (a) and unit cell (b)
1.2.3 交接角胞C
交接角胞C的交织结构和单胞模型如图5所示。设单胞的宽度和厚度分别用Wc、Tc表示,β1、β2、β3为内部编织角。根据基本假设和图中所示的几何关系,得到以下数学关系:
(3)
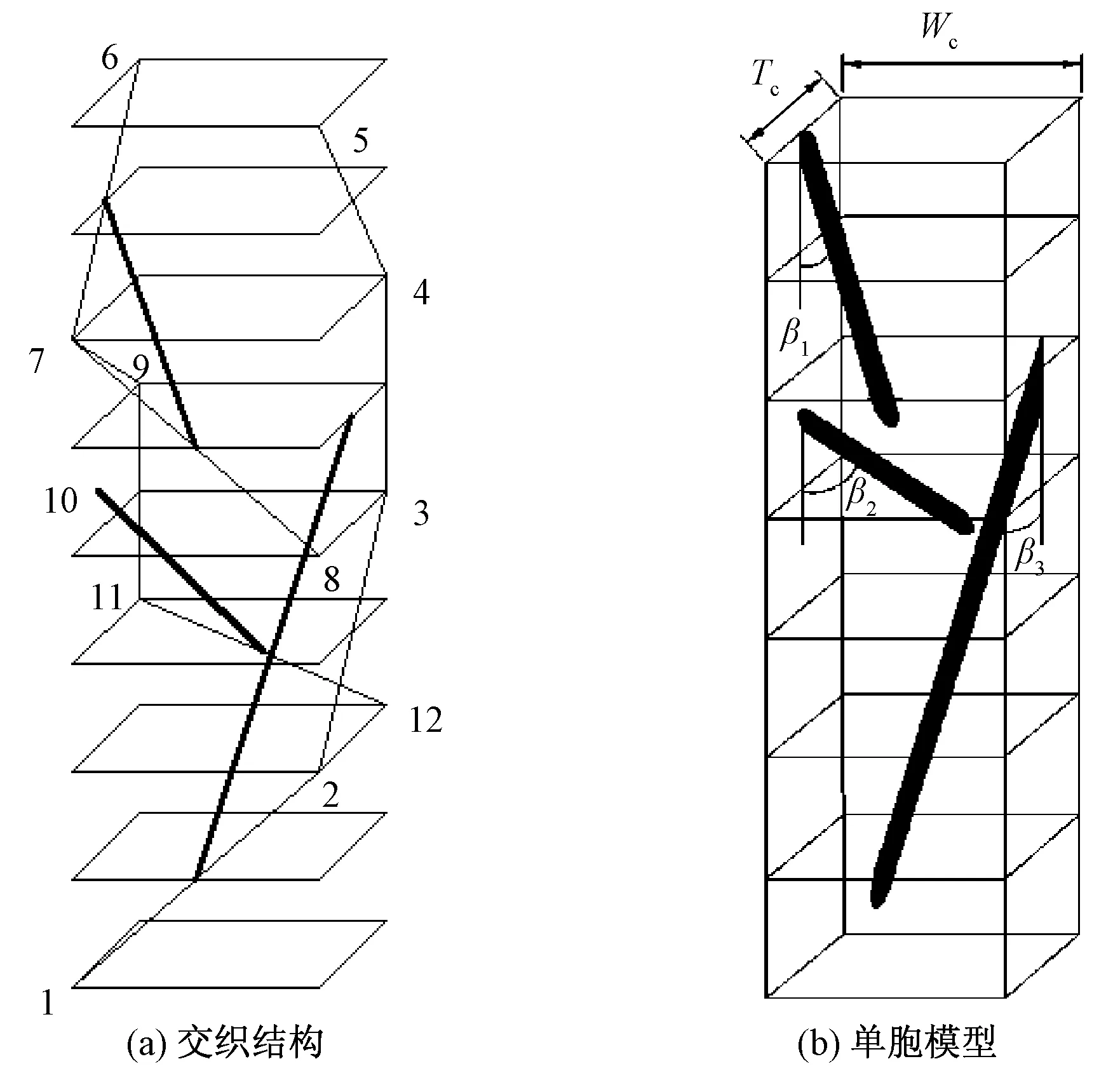
图区域交织结构和单胞模型Fig.5 Yarn structure (a) and unit cell
2 弯曲模量预测
目前对三维编织复合材料弯曲性能的预测主要有理论分析方法和有限元方法,对矩形组合截面三维编织复合材料,在有限元软件中建立完整的纱线结构,进行离散化处理求解,计算量庞大,不具可行性。本文利用文献[6]的基本思想,把矩形组合截面的三维编织物分成不同的矩形层,基于以上建立的单胞模型,运用弯曲刚度合成法预测T形截面三维编织复合材料的弯曲性能。
2.1 用弯曲刚度合成法的弯曲模量预测
将T形截面的三维编织复合材料试件分为表面层、内部层、交接层等5个部分,如图6所示。其中:表面层1由横向矩形宽度方向的表面单胞和棱角单胞组成;内部层1由横向矩形厚度方向的表面单胞和内部单胞组成;交接层由横向矩形宽度方向的表面单胞、棱角单胞及交接内胞、交接角胞S、交接角胞C组成;内部层2由纵向矩形厚度方向的表面单胞和内部单胞组成;表面层2由纵向矩形宽度方向的表面单胞和棱角单胞组成。在等应变条件下,通过坐标变换计算出各类单胞的刚度矩阵及单胞的纵向弹性模量,再根据各层的单胞构成情况,通过体积比计算出各层的刚度矩阵与弹性性能,进而预测整个试件的弹性模量。
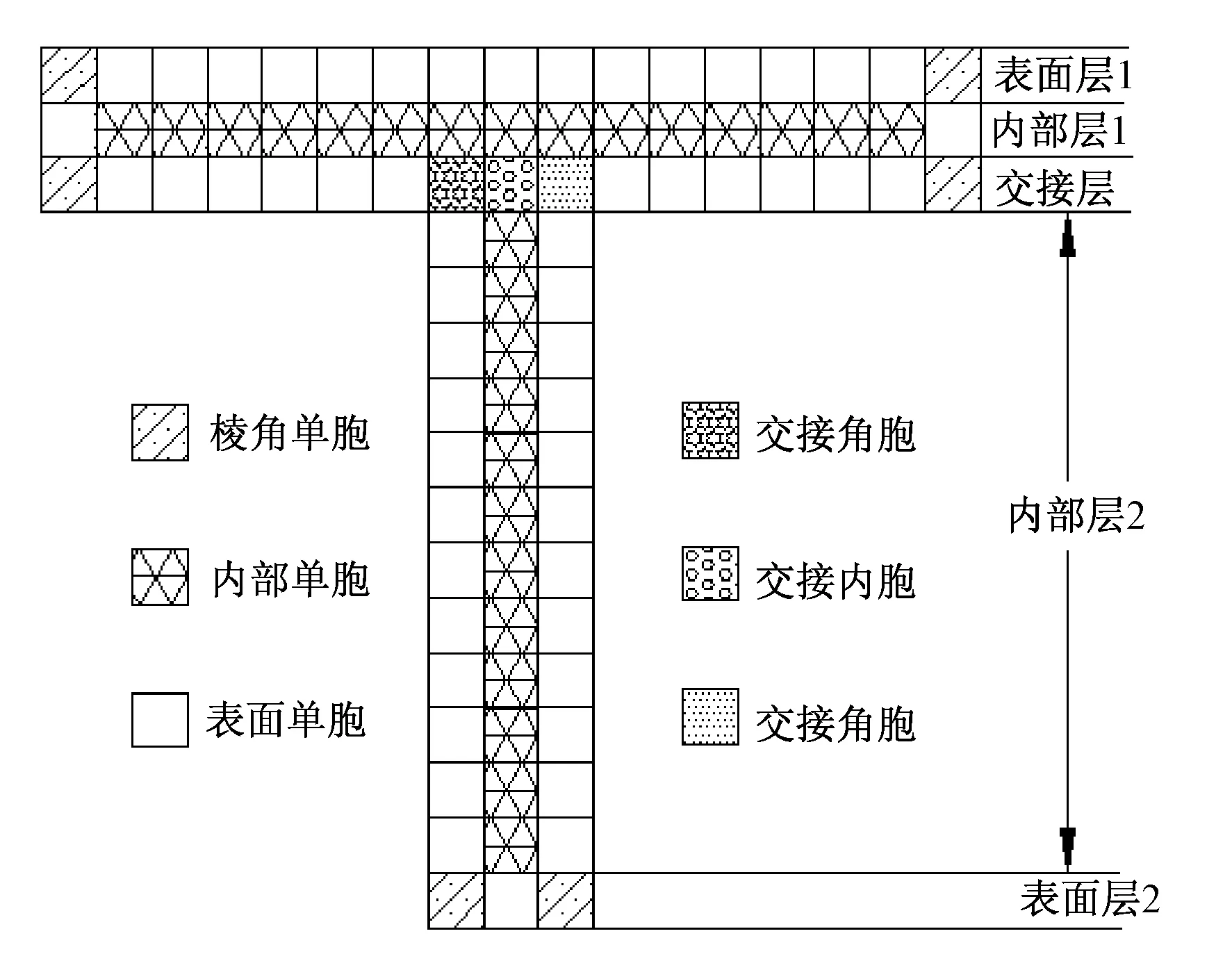
图6 T形截面分层Fig.6 Cross section of T beam
对纯弯曲试件,如果2个假设成立:1)平面假设,即弯曲时弯曲前原为平面的梁的横截面变形后仍保持平面,同一横截面的不同层之间保持相同的转角;2)纵向纤维间无正应力,则运用刚度合成法可得到
(4)
式中:E为T形截面三维编织复合材料的弯曲模量;Iy为T形截面的惯性矩;Ezk为每个矩形层Z向的弹性模量;Ik为每个矩形层的惯性矩。具体求解过程如下。
1)采用分解组合法,确定T形截面编织复合材料预制件各单胞的数量和分布。按图6所示的分层方法,共有6种单胞类型,假设分解后的矩形截面形状的主体纱为mk×nk(k=1,2),则内部单胞个数
(5)
表面单胞个数
(6)
交接内胞个数为n2-1,其余单胞个数及分布如图6所示。
2)根据各单胞的结构及编织参数之间的数学关系,计算各单胞纤维体积分数以及各单胞占整个预制件的体积百分比。矩形交接区域的3种单胞模型如前所述,其余区域的内部单胞、棱角单胞等参考常规矩形截面中的单胞模型。
3)运用刚度平均法计算各单胞的刚度矩阵。纤维束为横观各向同性材料,有5个独立的弹性常数,由纤维的弹性常数(弹性模量、泊松比等)写出单向复合纤维束的刚度矩阵,通过坐标变换将不同方向的纤维束刚度矩阵加权平均,再与基体的刚度矩阵线性相加,得到各个单胞的刚度矩阵。
4)根据每种单胞在矩形层中所占的体积百分数,计算各层的刚度矩阵,预测各层的弹性常数。
5)根据每个矩形层及T形截面尺寸求解惯性矩。
6)用MatLab编写预测T形截面三维编织复合材料弯曲模量的计算程序。
2.2 预测结果与分析
本文所预测的材料为三维编织玻璃纤维/树脂基复合材料,基体材料为环氧618,增强物为E1200玻璃纤维束。图7示出按上述方法预测的T形试件弯曲模量随编织角的变化规律,其中纤维体积含量为45%。从图中可看出,随着编织角的增加,弯曲模量逐渐减小。
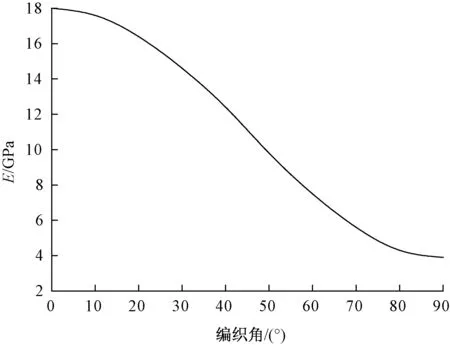
图7 弯曲模量E随编织角的变化情况Fig.7 Bending modulus variation with braiding angle
T形截面编织物中虽然存在特殊的细观结构,但是内部单胞、棱角单胞、表面单胞这3种单胞仍然占大多数,他们的数量及弹性性能是T型梁弯曲性能的重要影响因素,图8示出3种单胞弹性性能的比较结果。由图可见:内部单胞、棱角单胞、表面单胞的弹性性能均随编织角的增大而减小;棱角单胞、表面单胞的弹性模量略大于内胞的弹性模量。
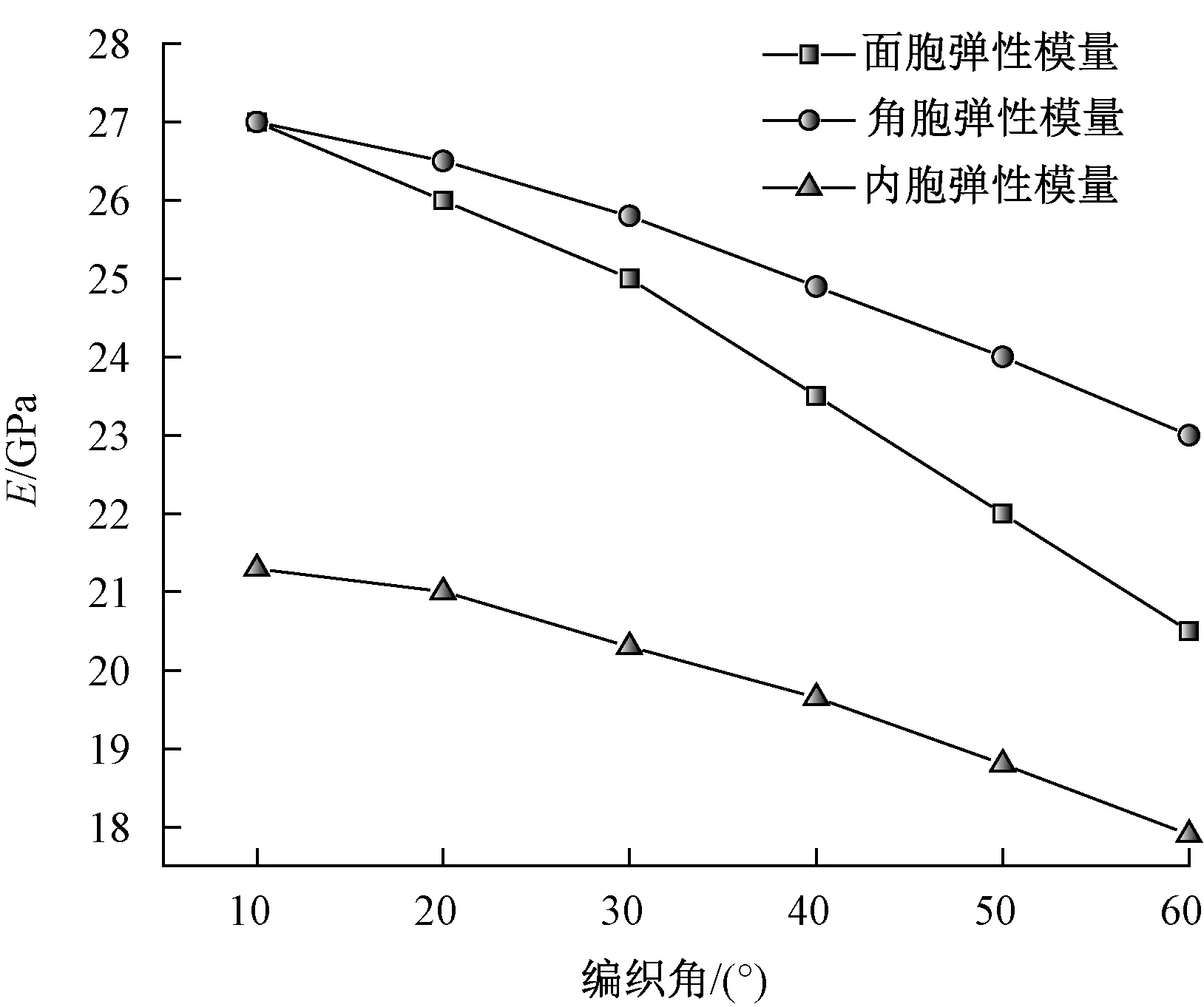
图8 不同单胞弹性模量的比较Fig.8 Comparison of elastic modulus of different cells
图9示出弯曲模量随纤维体积含量的变化规律。纤维体积含量越高,弯曲模量越大;编织角一定时,不同纤维体积含量的T形三维编织复合材料的弯曲模量变化比较均匀,差值δ近似恒定,得到的曲线图近似于几组平行线。材料的弯曲模量与材料的拉伸弹性性能有关,由内部单胞计算的等效弹性性能随编织角的增大,Z向等效弹性性能逐渐减小,弯曲时Z向的抗拉性能降低,则弯曲模量变小;当纤维体积含量增加时,材料的整体性能增强,抗弯能力提高,弯曲模量变大。

图9 弯曲模量随纤维体积含量的变化情况Fig.9 Bending modulus variation with fiber volume fraction
3 结果与分析
为验证预测结果的可靠性,本文对T形截面复合材料试件进行了三点弯曲试验,试件采用(RTM)成型,增强纤维为E1200玻璃纤维,基体为环氧618树脂,固化剂为苯二甲胺,增塑剂为邻苯二甲酸二丁酯。树脂与基体的配方质量比为10∶2∶1 (环氧树脂∶固化剂∶增塑剂)。2组试件分别为三维四向(试件编号分别为:TW2045D4、TW3545D4)和三维五向(试件编号分别为TW2045D5、TW3545D5),编织角分别为20°和35°,纤维体积含量为45%,每组试件各3个。试验在美斯特万能电子试验机上进行,图10为测试方法示意图。
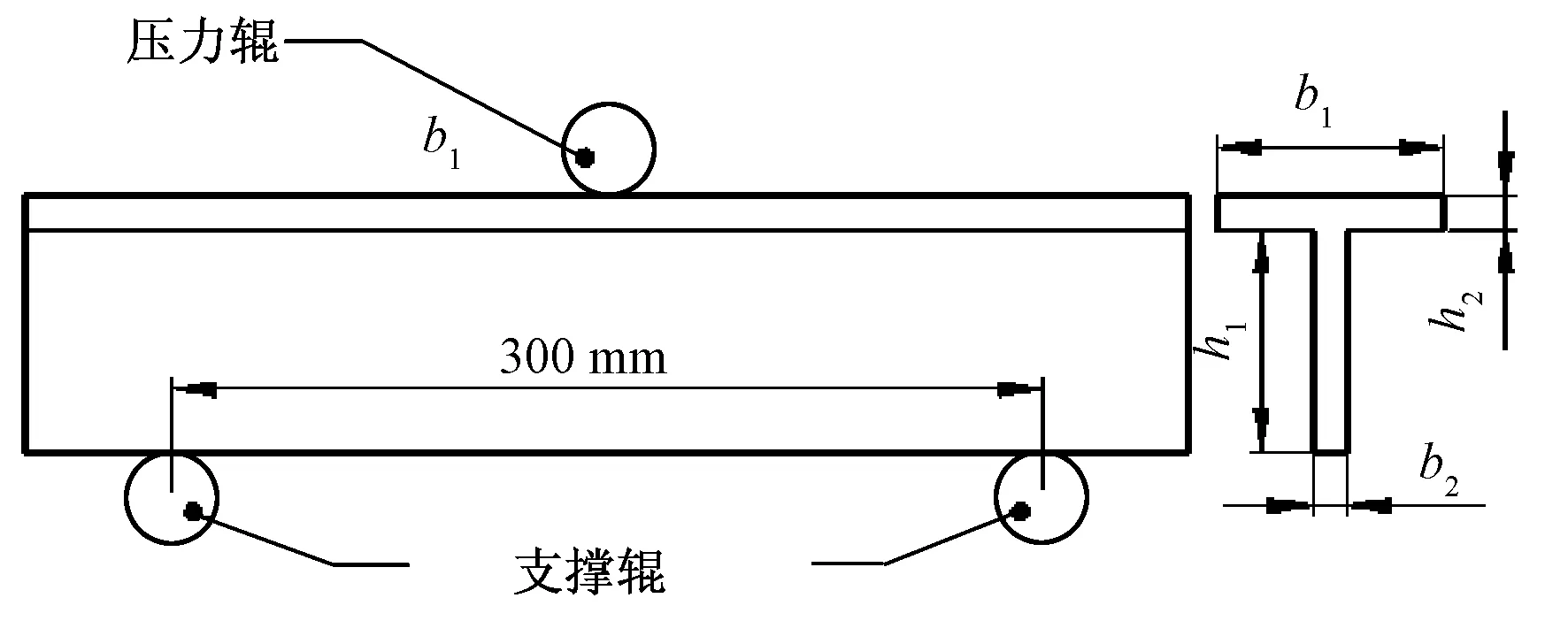
图10 三点弯曲试验示意图Fig.10 Schematic diagram of three-point bending test
试验中采用3个相同直径的金属圆辊,材料筋高朝下放置在2个支撑辊上,2支撑辊间距为300 mm。试件长500 mm,截面尺寸b2=h2=4 mm,b1=h1=26 mm。试验机由计算机控制加载,压辊的加载速率为2 mm/min,传感器自动采集数据,加载过程,载荷随时间线性增加,记录不同载荷作用时试件的最大挠度,计算弯曲模量。每组试件取3次试验的平均值作为最终结果,如表1所示。从表可看出:试件TW2045D4的弯曲模量为14.45 GPa,大于试件TW3545D4的弯曲模量12.26 GPa,符合预测趋势,即随着编织角的增大弯曲模量减小;试件TW3545D5的弯曲模量18.23 GPa,大于试件TW3545D4的弯曲模量12.26 GPa,尽管试件的数量较少,但是2组试件的比较能体现出三维五向的弯曲性能优于三维四向。
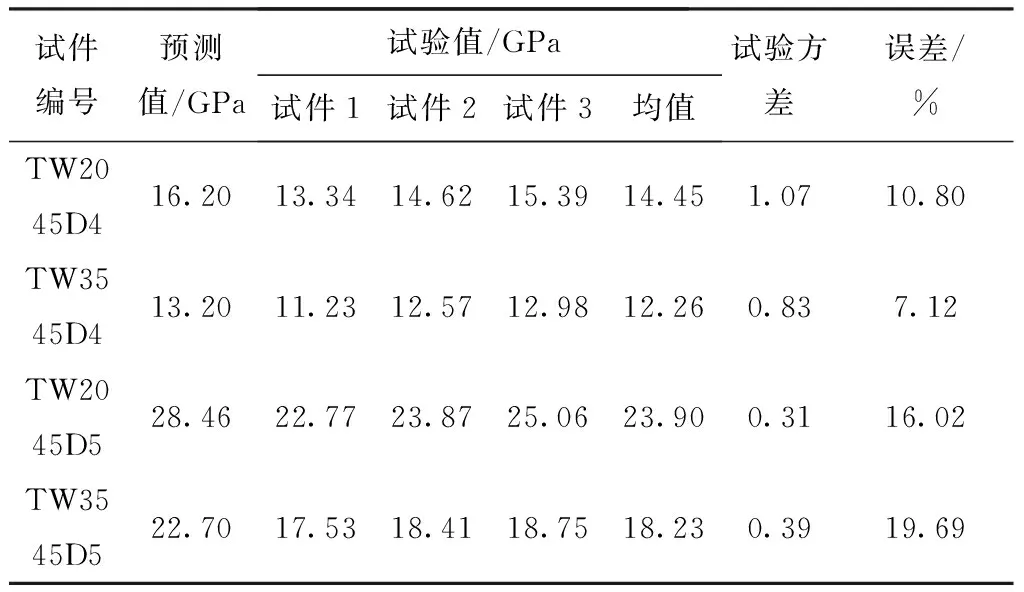
表1 弯曲试验结果
2组试验结果都可看出,试验值小于理论预测值。分析原因为:一方面是理论计算时把材料设定为理想状态,并作出很多假设,这使得理论值本身就会比试验值偏大;同时,当制备的试件截面尺寸较小时,由于棱角单胞及表面单胞不可忽略,仅用内部单胞预测等效弹性模量势必存在误差。另一方面试件的质量是影响试验结果的重要影响因素,在试件制作过程中,从编织到预制件的复合成型不确定因素很多,试件结构是否均匀、注胶过程中是否存在气泡、固化时间和温度的差异都会对试件质量产生影响。上述原因使得理论预测值和试验值存在一定的差异,但4组数据并无显著性差异,运用弯曲刚度合成法预测弯曲模量仍能获得有价值的结论,对T形截面复合材料的工程应用具有重要的参考价值。
4 结束语
本文根据矩形组合截面编织物的编织工艺,通过分析载纱器的水平运动规律,得到编织纱线的空间路径,运用控制体积法建立了T形截面三维编织复合材料交接区域的特殊细观模型。以此细观结构为基础,运用刚度合成法,预测了T形截面三维编织复合材料的弯曲性能,用MatLab编写了预测弯曲模量的参数化运算程序。由计算结果分析了弯曲模量随编织参数的变化规律,并进行了弯曲性能试验,试验结果与预测结果进行了比较分析。虽然弯曲刚度合成法预测的弯曲模量与试验值存在一定的偏差,但在实际工程使用中,预测值依然具有重要的参考价值。
FZXB
[1] 练军,顾伯洪. 三维编织复合材料动态冲击性能的数值模拟[J]. 纺织学报,2011, 32(1):41-50. LIAN Jun,GU Bohong.Numerical simulation of dynamic performance of three-dimensional braided compo-sites[J]. Journal of Textile Research,2011, 32(1):41-50.
[2] 程灿灿,刘兆麟. 三维编织复合材料弯曲性能研究进展[J]. 产业用纺织品,2012(4):1-5. CHENG Cancan, LIU Zhaolin. Progress in research on flexural properties of 3D braided composites[J]. Technical Textiles, 2012(4):1-5.
[3] 陈利,李嘉禄,李学明. 三维四向编织复合材料弯曲性能的预测[J]. 天津工业大学学报,2003,22(2):1-5. CHEN Li, LI Jialu, LI Xueming. Prediction of the bending properties of three-dimensional four-directional braided composite[J]. Journal of Tianjin Polytechnic University,2003,22(2):1-5.
[4] 王波,矫桂琼,陶亮,等. 三维编织T300/QY9512弯曲性能的实验研究[J].西北工业大学学报,2003,21 (5):552-555. WANG Bo, JIAO Guiqiong, TAO Liang,et al. Bending experiment investigation of 3-D braided T300/QY9512 composite[J]. Journal of Northwestern Polytechnical University,2003,21 (5):552-555.
[5] 王波,矫桂琼,陶亮. 三维编织复合材料弯曲性能分析[J].固体力学学报,2004,25(1):75-79. WANG Bo, JIAO Guiqiong, TAO Liang. Flexure property analysis of three-dimensional braided composite[J].Chinese Journal of Solid Mechanics, 2004,25(1):75-79.
[6] 李典森,许晓燕,卢子兴,等. 三维多向编织复合材料弯曲模量的理论预测[J]. 机械强度,2008,30(4):623-627. LI Diansen, XU Xiaoyan, LU Zixing,et al. Theoretical prediction for the bending modulus of three-dimensional and multi-directional braided composites[J]. Journal of Mechanical Strength, 2008,30(4):623-627.
[7] ZHANG Wei, DING Xin, LI Yuling. Microstructure of 3D braided preform for composites with complex rectangular cross-section[J]. Journal of Composite Materials, 2007,41(25):2975-2983.
[8] ZHANG Wei, DING Xin, LI Yuling. Calculation and design of parameters for four-step 3D braided preform with complex rectangular cross sections[J]. Journal of Industrial Textiles,2008, 38(2):139-150.
[9] 陈光伟,陈利,李嘉禄,等. 三维多向编织复合材料T型梁抗弯应力分析[J]. 纺织学报,2009, 30(8):54-58. CHEN Guangwei, CHEN Li, LI Jialu, et al. Study on flexural stress of T beam of 3-D multidirectional braided composites[J].Journal of Textile Research,2009, 30(8):54-58.
[10] 董纪伟,冯淼林,陈文,等. 基于均匀化理论的三维编织复合材料弯曲细观应力数值模拟[J].材料科学与工程学报,2010,28(6): 801-806. DONG Jiwei, FENG Miaolin, CHEN Wen, et al. Homogenization-based method for simulating micro bending stress of 3-D braided composites[J]. Journal of Materials Science and Engineering, 2010,28(6): 801-806.
[11] ZHAO Qiang, JIN Limin, JIANG Lili,et al.Experimental characterizations of bending fatigue of a four-step 3-D braided rectangular composite under different stress levels[J]. Journal of Reinforced Plastics and Composites, 2011,30(18):1571-1582.
[12] SUN Baozhong, LIU Ruiqiang, GU Bohong.Numerical simulation of three-point bending fatigue of four-step 3-D braided rectangular composite under different stress levels from unit-cell approach[J].Computational Materials Science, 2012,65:239-246.
[13] 张中伟,严静. 三维编织复合材料 T 型梁弯曲疲劳性能研究[J]. 玻璃钢/复合材料,2014(4):42-45. ZHANG Zhongwei, YAN Jing. Bending fatigue behavior of 3D braided composite T-beam [J].Fiber Reinforced Plastics/Composites, 2014(4):42-45.
Micro-structure analysis and bending property prediction of three-dimensional braided composites with T section
YU Chenchen, QU Chang, DENG Jie, DAI Aibo, ZHANG Xiaoping
(College of Mechanical Engineering, Nantong University, Nantong, Jiangsu 226019, China)
According to the 4-step braiding principle of preforms with complex rectangular cross section, the yarns paths in braided preforms with T section were analyzed. The spatial paths of yarns were speculated in accordance with the movements of carriers. By the volume-control method, the special micro-structure model in the join region of composites with T section was established. Assuming the yarn cross-section is an ellipse and under other ideal conditions, the mathematical relationship between braiding parameters was deduced. The bending modulus was predicted by the MatLab program which was developed based on bending stiffness synthesis method. The results showed that bending modulus decreased with braiding angle increasing and increased with fiber volume increasing, and bending property of T beam of three dimensional five directional braided composites was superior to T beam of three dimensional four directional braided composites. Finally, compared with the experimental results, the validity of bending property predicted by this method was verified.
three-dimensional braiding; T section; micro-structure; bending property
10.13475/j.fzxb.20140403808
2014-04-12
2015-03-12
南通市应用研究计划项目(BK2012006)
于陈陈(1990—),男,硕士生。主要研究方向为虚拟仿真。瞿畅,通信作者,E-mail:xu.ch@ntu.edu.cn。
TS 181
A
