基于改进K-SVD和非局部正则化的图像去噪

杨爱萍,田玉针,何宇清,董翠翠

(天津大学电子信息工程学院,天津300072)

基于改进K-SVD和非局部正则化的图像去噪

杨爱萍,田玉针,何宇清,董翠翠

(天津大学电子信息工程学院,天津300072)

K-奇异值分解(K-SVD)算法在强噪声下的去噪性能较差。为此,提出一种新的图像去噪算法。使用相关系数匹配准则和噪声原子裁剪方法改进传统K-SVD算法,提高原算法的去噪性能,将非局部正则项融入图像去噪模型,并采用非局部自相似性进一步改善图像的去噪效果。实验结果表明,与传统K-SVD算法相比,该算法在提高同质区域平滑性的同时,能保留更多的纹理、边缘等细节特征。

图像去噪;稀疏表示;奇异值分解;正交匹配追踪算法;字典优化;非局部自相似性

1 概述

基于稀疏表示的图像去噪成为近年来该领域的前沿研究课题。其主要利用过完备字典［1-3］的冗余性对图像进行稀疏表示,能够有效地捕捉图像的结构特征,在去除噪声的同时更好地保持图像信息。其中,文献［4］提出K-奇异值分解(K-Singular Value Decomposition,K-SVD)原子库训练和稀疏表示方法,在去除轻度图像噪声方面表现出较好的去噪性能。但在噪声污染较严重的情况下,其图像恢复效果并不理想,当用带噪图像本身作为训练样本时,面临信号特征提取和噪声抑制之间的矛盾,得到的字典中往往含有大量噪声原子。

另一方面,基于字典学习的K-SVD去噪算法,只是利用待处理图像块内部的信息进行独立稀疏编码,没有充分考虑与其他样本图像的相关信息,如块与块之间的重叠性、相似性等,对先验信息的表达能力不足。另一方面在过完备字典上的稀疏分解是潜在不稳定问题,容易产生视觉伪像。

针对上述问题,在研究基于K-SVD字典学习的图像去噪算法基础上,本文将相关系数匹配准则［5］和字典裁剪方法相结合,考虑到图像一般存在大量的重复模块,位于不用位置的图像块往往表现出很强的非局部自相似性［6-7］。为了充分利用图像的非局部自相似性信息,提出将非局部自相似性作为一个约束正则项融入到图像去噪模型,得到基于改进K-SVD字典学习和非局部正则化的图像去噪算法。

2 基于稀疏表示的图像去噪

设数字图像用矩阵Y∈ℝN表示,大小为N×N,字典矩阵D由L个N维向量的dij组成,dij称为字典原子。当D给定时,图像Y可表示为字典原子的线性组合:

其中,αij为 Y在字典 D上的稀疏表示系数;矩阵R(M)是经过 M项逼近后的残差项。本文采用 KSVD方法进行字典训练得到的字典D,并将其用于图像去噪。用矩阵X表示原始图像,则图像的去噪模型为:

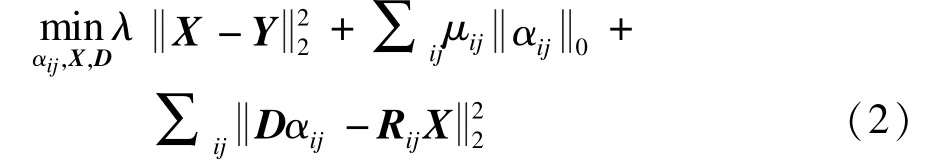
去噪过程为:初始化字典D和图像X,利用正交匹配追踪(Orthonormal Matching Pursuit,OMP)［8-9］算法求得稀疏表示系数αij;其次,根据得到的稀疏系数αij,利用K-SVD算法更新字典D;最后,当D和系数αij均达到要求时,根据下式求得去噪图像:

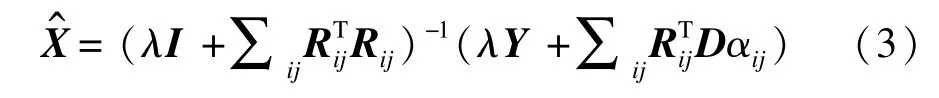
其中,I为单位矩阵;X^表示去噪后的图像矩阵。

3 K-SVD算法优化

K-SVD算法得到的是全局过完备字典。但是在强噪声的情况下,字典中含有大量与噪声匹配的噪声原子,导致在字典学习训练过程中,无法达到有效去除噪声的目的。本文对基于K-SVD的字典学习方法进行改进。一方面,在稀疏编码环节,引入相关系数匹配准则,提取更多有意义的结构训练得到更优的字典,实现对图像信号更准确的逼近;另一方面,基于噪声原子剪裁对训练字典进一步优化。将上述2种方法相结合得到改进K-SVD算法,形成一种有效的字典训练方法。

3.1 基于相关系数匹配准则的稀疏编码

稀疏编码在字典学习中计算信号在给定字典下的稀疏表示系数。为了得到自适应性强的字典,通常选择含噪图像本身作为训练样本,由此就会导致信号提取和噪声抑制相矛盾的问题。

目前,字典学习方法的迭代停止准则多采用基于残差信号能量的迭代停止标准［10-11］。但是,当噪声强度和信号维数 n变大时,该准则将过早终止OMP迭代,导致遗漏了有用信号。文献［5］研究了相关函数局部最大值与信号特征之间关系,在此基础上提出了一种新的基于相关系数匹配的停止准则。定义匹配因子为第j次迭代时残差信号矩阵Rj-1f和字典原子gγ之间的相关系数:

匹配因子的最大值会随着信号的不断提取而降低,当信号的有用信息已被全部提取完毕,即残差信号中基本上没有有用信息时,匹配因子的最大值也就降到了理想值,此时,停止OMP迭代。假设Tm为设定的阈值,则停止准则如下:

3.2 基于噪声原子剪裁的字典优化

当训练样本采用含噪图像块时,基于K-SVD方法训练得到的字典中含有与噪声匹配的噪声原子,噪声原子的存在将严重影响图像的去噪质量。因此,需要尽可能地从字典中删除这些噪声原子对字典进行优化,其核心问题是如何对噪声原子进行检测。文献［12］提出利用假设检验来检测噪声原子,其利用信号原子至少在一个方向上相关性很强,而纯噪声原子在各个方向上的相关性都几乎没有。存在相关性的方向上特征向量的方差会很小,即各个方向的特征向量的方差会有所差别。

本文采用Bartlett检验法［12］,设vi是特征向量的方差。用Bartlett检验测试原子在4个方向上的特征向量的方差vi是否相等或者至少有2个原子的方差不等,定义Bartlett检验统计量为:

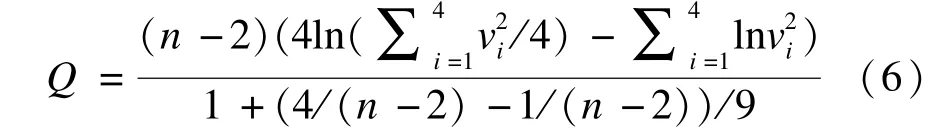
对原子库中的原子进行判断,若某原子满足Q＜χ2(α;3),则认为该原子只含有噪声成分,并从原子库中删除,其中,χ2(α;3)表示自由度为3的chi-平方分布的上α百分点位置。与传统的字典优化方法不同［13］,上述方法只是从字典中删除噪声原子,不会影响字典的信息原子,提高了去噪后的图像质量。

3.3 改进的K-SVD字典训练方法

将基于相关系数匹配准则的稀疏编码方法以及噪声原子剪裁方法相结合,用于K-SVD字典训,得到一种改进的K-SVD字典训练方法。

字典的学习是通过稀疏编码和字典更新2个步骤交替进行来完成。整个学习过程分为2个阶段:阶段1得到一个初始字典;阶段2对字典进行优化。在阶段1,运用传统的K-SVD的方法进行字典训练,用OMP算法进行稀疏编码,以残差能量值小于n(Cσ2)作为终止条件。阶段2运用相关系数匹配准则进行稀疏编码,并对阶段1的字典进行优化。算法步骤如下:

(1)得到一个初始字典

设定初值:如果σ＜5,则令maxiter=5;否则,令maxiter=10。

当j＜maxiter时,循环执行以下步骤:

2)字典更新:对每个原子进行SVD分解。

(2)对字典进行优化设定初值:令maxiter=6, Tm=0.06,α=0.01。

当j＜maxiter时,循环执行以下步骤:

2)字典更新:对每个原子进行SVD分解。

3)字典优化:进行噪声检测并删除噪声原子。

4 图像的非局部自相似性

如前所述,K-SVD字典学习去噪方法,只是利用图像块内部信息进行独立稀疏编码,并没有充分考虑其他样本图像的相关信息,对先验信息的表达能力不足;同时,过完备字典下的稀疏分解是潜在不稳定问题。因此,有必要在去噪模型中引入正则化项。考虑到图像一般存在大量的重复模块,不同位置的图像块往往表现出很强的自相似性。为了充分利用图像的非局部自相似性信息,本文提出将其作为一个正则化先验约束项融入到图像去噪模型。

文献［14-15］提出非局部均值滤波(Nonlocal Means Filtering,NLF)去噪方法。设矩阵Y为含噪图像,给定像素 i,其 NLF滤波强度值定义为NLF(i),它由像素点周围搜索窗内像素点的权重构成。像素i相对于像素j的权重记为w(i,j),权重值由这些像素之间的相似性决定,相似性的计算是通过以这些像素为中心的块之间的高斯l2距离。例如,设i和j分别为大小为b×b的图像块矩阵Ni,Nj的中心像素,并假设j位于像素i的大小为L×L的搜索窗内。w(i,j)的计算公式为:

其中,S(i)表示归一化系数;h=0.5σ2是高斯核的控制因子;σ高斯核的标准差。对图像矩阵Y的各个像素计算器权重w(i,j),得到权重矩阵W,根据上述定义建立一个非局部正则化项(Nonlocal Regularization,NR)［7,16］:

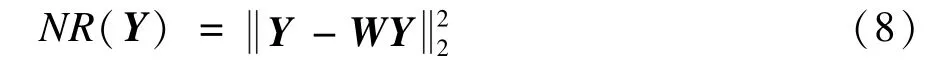
5 本文算法

本文提出基于改进的K-SVD字典学习,将图像的非局部自相似性作为图像先验信息融入到基于稀疏表示的图像去噪模型中,即将式(8)添加到式(2)中,得到新的去噪模型:

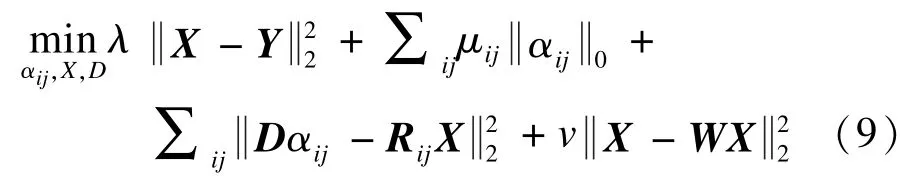
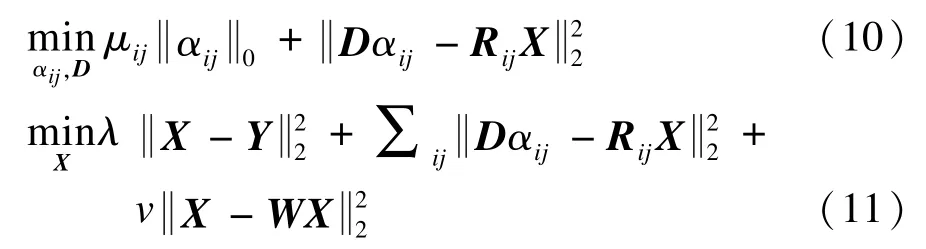
为解决第一个子问题,先初始化原始图像的估计,即令X=Y。采用块协调最小化方法求解这个子问题,可分为2个步骤:(1)初始化字典D∈ℝn×K(K＞n)为超完备的DCT字典,根据已知的X和D,采用基于相关系数匹配准则的OMP算法进行稀疏编码得到稀疏表示系数αij;(2)在已知X,D和αij的情况下,采用改进K-SVD的字典学习算法更新过完备稀疏表示字典和稀疏表示系数ij,此步骤迭代J次。

为解决第2个子问题,先利用式(7)的方法计算自相似性权重矩阵W。然后将更新后的过完备稀疏表示字典矩阵、稀疏表示系数ij以及权重矩阵W代入下式,得到原始图像的估计矩阵X^:

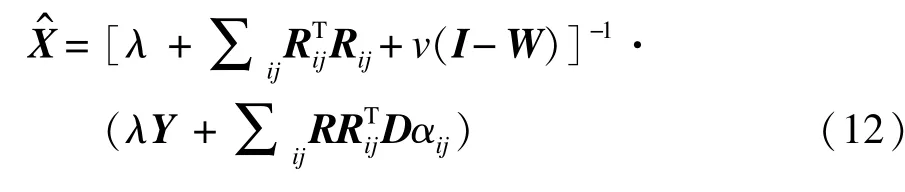
6 实验结果及分析

为了验证本文算法的有效性,本节将其与同类方法K-SVD［11］、改进K-SVD(K-SVD_N)、NLM［6］进行比较。测试图像为512×512像素的灰度图像Lena、Barbara、Boat和256×256像素的灰度图像Cameraman、Peppers。添加均值为0、标准差为σ的高斯白噪声。字典矩阵D的原子数目K=256,训练图像块大小取值范围是6～16,这里取6×6, K-SVD算法迭代次数J取10。Langrage乘子和残差因子的取值均与高斯噪声方差有关,根据文献［1］,分别设为λ=30/σ,Tm=(1.15σ)2。根据实验经验,令非局部正则项参数b=7,L=21。

图1给出了4种算法对Boat图像去噪后的峰值信噪比(Peak Signal to Noise,PSNR)曲线。表1给出了4种算法在不同噪声强度下的去噪结果,其中,加粗的数据为在相同情况下,PSNR值最高的数据。由表1和图1可知,本文算法明显优于其他3种算法。同一噪声强度下,本文提出的K-SVD-N-NL算法比改进的K-SVD算法(New K-SVD,K-SVD-N)、非局部均值算法(Non-local Mean,NLM)去噪后PSNR值大。随着噪声强度σ的增大,本文算法优势更加突出,当噪声强度很高时,优势可达3 dB～4 dB。

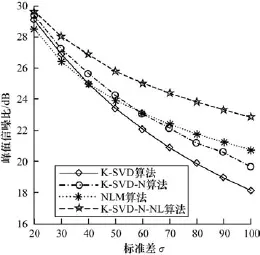
图1 去噪图像PSNR曲线

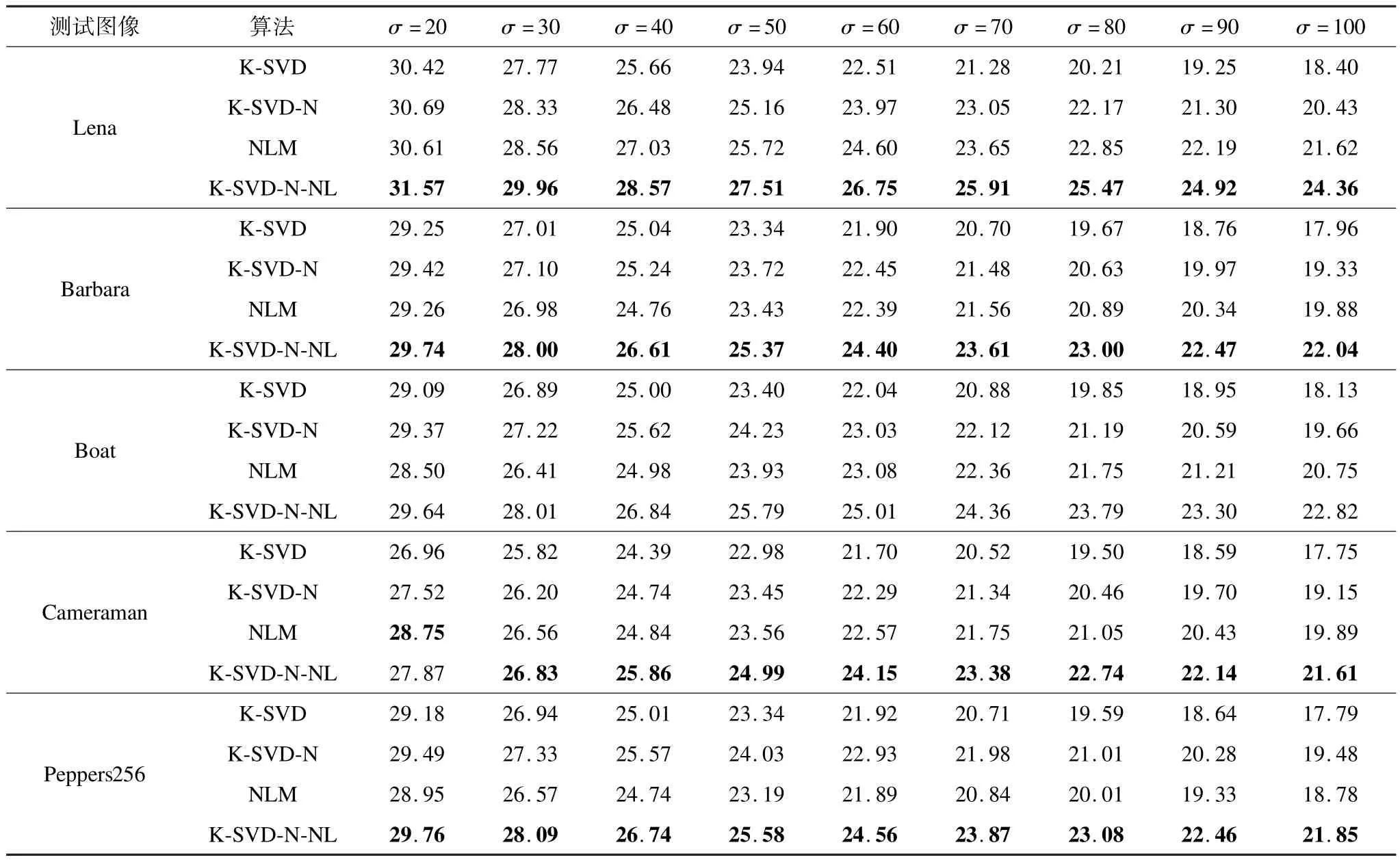
表1 去噪图像的PSNR值比较dB

图2为σ=30时,4种算法对Lena图像去噪后的效果图,图3为局部放大效果。在噪声强度一定时,K-SVD-N算法虽然保持了纹理边缘结构,但是容易在平滑区造成褶皱现象;NLM算法去除了大部分噪声,但造成图像的过平滑,纹理结构不清晰,如头发纹理变得不清晰;本文算法不但去除了平滑区的噪声,减轻了平滑区的褶皱现象,并较好地保持了边缘纹理等细节信息。

图2 σ=30时4种算法的去噪效果

图3 去噪图像局部放大结果

需要说明的是,本文算法是在改进K-SVD算法的基础上添加了非局部自相似约束,即式(9)中最后一项,因此,本文算法的复杂度略有增加。

7 结束语

为了对噪声强度较大的图像进行去噪,本文提出一种基于稀疏表示和非局部正则项的去噪算法。该算法不仅考虑了图像特征提取和噪声原子抑制,在字典训练中引入基于相关系数匹配的稀疏编码和基于原子库裁剪的字典优化,同时还考虑了图像的非局部自相似性,在去噪模型中引入非局部正则化项。实验结果表明,与同类去噪算法相比,该算法不但去除了平滑区的噪声,减轻了平滑区的褶皱现象,而且能较好地保持边缘纹理等细节信息。今后将研究如何在保证去噪效果的同时,加快算法的运行速度。

［1］Elad M.Sparse and Redundant Representations:From Theory to Applications in Signal and Image Processing［M］.Berlin,Germany:Springer,2010.

［2］Candes E J,Donoho D L.Recovering Edges in Ill-posed Inverse Problems:Optimality of Curvelet Frames［J］. Annals of Statistics,2002,30(3):784-842.

［3］孙林慧,杨 震.基于数据驱动字典和稀疏表示的语音增强［J］.信号处理,2011,27(12):1793-1800.

［4］Aharon M,Elad M,Bruckstein A M.K-SVD and Its Non-negative Variant for Dictionary Design［C］// Proceedings of International Society for Optics and Photonics.San Diego,USA:Society of Photo-optical Instrumentation Engineers,2005.

［5］Lee R J,Nicewander W A.Thirteen Ways to Look at the Correlation Coefficient［J］.The American Statistician, 1988,42(1):59-66.

［6］Chen Lixia,Liu Xujiao.NonlocalSimilarity Based Coupled Dictionary Learning for Image Denoising［J］. Journal of Computational Information Systems,2013, 9(11):4451-4458.

［7］Zhang Jian,Liu Shaohui,Xiong Ruiqin,et al.Improved TotalVariation Based Image Compressive Sensing Recovery by Nonlocal Regularization［C］//Proceedings of IEEE InternationalSymposium on Circuitsand Systems.Washington D.C.,USA:IEEE Press,2013: 2836-2839.

［8］Donoho D L,Tsaig Y,Drori I,et al.Sparse Solution of Underdetermined Systems ofLinearEquations by StagewiseOrthogonalMatching Pursuit［J］.IEEE Transactions on Information Theory,2012,58(2): 1094-1121.

［9］赵海峰,鲁毓苗,陆 明,等.基于快速稀疏表示的医学图像压缩［J］.计算机工程,2014,40(4):233-236.

［10］Protter M,Elad M.ImageSequenceDenoising via Sparse and RedundantRepresentations［J］.IEEE Transactions on Image Processing,2009,18(1):27-35.

［11］Elad M,Aharon M.Image Denoising via Sparse and Redundant Representation over Learned Dictionaries［J］.IEEE Transactions on Image Processing,2006, 15(12):3736-3745.

［12］Bartlett M S.Properties of Sufficiency and Statistical Tests［J］.Proceedings of the Royal Society of London. Series A,Mathematical and Physical Sciences,1937, 160(901):268-282.

［13］Mazhar R,Gader P D.EK-SVD:Optimized Dictionary Design for Sparse Representations［C］//Proceedings of the 19th IEEE International Conference on Pattern Recognition.Washington D.C.,USA:IEEE Press,2008:1-4.

［14］Buades A,Coll B,Morel J M.A Review of Image Denoising Algorithms,with a New One［J］.Multiscale Modeling&Simulation,2005,4(2):490-530.

［15］刘晓明,田 雨,何 徽,等.一种改进的非局部均值图像去噪算法［J］.计算机工程,2012,38(4):199-201.

［16］Dong Weisheng,Zhang Lei,Shi Guangming,et al. Nonlocally Centralized Sparse Representation for Image Restoration［J］.IEEE Transactions on Image Processing,2013,22(4):1620-1630.

编辑 刘 冰

Image Denoising Based on Improved K-SVD and Non-local Regularization

YANG Aiping,TIAN Yuzhen,HE Yuqing,DONG Cuicui
(School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China)

In view of the poor performance of the K-Singular Value Decomposition(K-SVD)denoising method,a new algorithm is proposed.The denoising performance is improved by the refined K-SVD method with the help of the correlation coefficient matching criterion and dictionary cutting method.By combining the non-local self-similarity as a constrained regularization into the image denoising model,the performance is further enhanced.Experimental results show that compared with traditional K-SVD method,this algorithm can effectively improve the smoothness of homogeneous regions with preserving more texture and edge details.

image denoising;sparse representation;Singular Value Decomposition(SVD);Orthonomal Matching Pursuit(OMP)algorithm;dictionary optimization;non-local self-similarity

1000-3428(2015)05-0249-05

A

TP391

10.3969/j.issn.1000-3428.2015.05.046

国家自然科学基金资助项目(61372145)。

杨爱萍(1977-),女,副教授、博士,主研方向:图像处理;田玉针,硕士;何宇清,讲师、博士;董翠翠,硕士。

2014-04-30

2014-07-07E-mail:yangaiping@tju.edu.cn

中文引用格式:杨爱萍,田玉针,何宇清,等.基于改进K-SVD和非局部正则化的图像去噪［J］.计算机工程,2015, 41(5):249-253.

英文引用格式:Yang Aiping,Tian Yuzhen,He Yuqing,et al.Image Denoising Based on Improved K-SVD and Non-local Regularization［J］.Computer Engineering,2015,41(5):249-253.