一种新的灰度非均匀图像分割模型

王 瑜,闫 沫

(1.西安航空学院机械学院,西安710077;2.西安建筑科技大学机电工程学院,西安710055)

一种新的灰度非均匀图像分割模型

王 瑜1,闫 沫2

(1.西安航空学院机械学院,西安710077;2.西安建筑科技大学机电工程学院,西安710055)

基于局部区域的主动轮廓分割模型在针对灰度非均匀图像进行分割时,容易受到初始轮廓曲线位置的影响,且基于水平集模型的数值实现速度较慢。为此,提出一种新的图像分割模型。该模型采用局部符号差能量项作为曲线演化的驱动力,为减少模型对初始轮廓曲线位置的依赖,采用全局凸分割策略,得到一个离散化的凸分割模型,该模型包含Mumford-Shah分割模型中的二次光滑项,使分割后的区域更加平滑,使用split Bregman迭代算法进行数值实现。实验结果表明,与局部二值拟合模型、局部符号差能量模型相比,该模型能对灰度非均匀图像进行较准确的分割,具有较快的运算速度和较好的鲁棒性。

图像分割;局部区域;灰度非均匀;主动轮廓模型;split Bregman迭代

1 概述

图像分割是图像处理领域中所要研究的基本问题。在过去的数10年间出现了许多基于不同理论的分割算法。其中,基于水平集(Level Set,LS)算法的主动轮廓模型(Active Contour Model,ACM)以其坚实的理论基础和较好的分割效果受到研究人员的广泛关注。它的基本思想是:在一定的条件下,利用驱动力引导水平集轮廓曲线朝着目标边界进行演化。根据驱动力的不同,主动轮廓模型大致分为基于边界的模型［1-3］和基于区域［4-6］的模型。基于边界的模型通常对噪声和弱边缘较为敏感,基于区域的模型使用了全局信息,因此,相比前者具有更好的分割效果。

在现实生活中,由于成像设备本身或者光照变化等因素的影响,自然图像往往表现出灰度非均匀性。这使得基于无边界主动轮廓(Active Contours Without Edges,ACWE)［4］的分割模型在针对非均匀图像进行分割时,往往无法获得满意的效果。针对该类问题,Mumford-Shah(MS)模型［7］表现出较好适应性,然而由于MS模型本身是非凸的,算法容易陷入局部极小点。同时,该模型的求解较为困难,算法运行速度较慢。近年来以ACWE模型为基础的基于局部区域的主动轮廓模型相继被提出［8-11］。这类模型在曲线演化的驱动力中加入了局部区域的灰度信息,使得这些模型具有局部可分离性。在针对非均匀图像时,获得了较好的分割结果。然而在这些模型中,一个严重的缺陷是它们都对初始轮廓的位置较为敏感。为了获得较好的分割效果,往往需要精心挑选初始轮廓曲线的位置,这大大限制了该类模型在实际中的应用。另一方面,由于曲线的演化需要考虑局部区域信息,因此采用水平集方法进行曲线演化时,每次迭代都需要进行大量计算,这使得算法的演化速度很慢。针对这些问题,文献［12］提出一种基于区域的局部符号差(Local Signed Difference,LSD)能量的主动轮廓模型。该模型由于同时考虑局部区域的信息和聚类顺序,因此受水平集初始轮廓曲线影响较小。另一方面,LSD能量项仅需计算一次,因此,模型的求解时间很快,几乎可以与经典的ACWE模型相比较。文献［12］同时指出该模型的局限是要求目标区域同背景区域相比更亮或更暗,对具有细密纹理的图像也无法获得满意的结果。

针对这些模型的限制,本文提出一种新的分割模型,将LSD能量项作为数据项,在模型中采用全变分(Total Variation,TV)项作为分割边界的正则项,引入MS模型的二次光滑项。由于该项具有较好的平滑作用,因此对于具有细密纹理、明暗变化复杂的图像具有较好的分割效果,为了减少对初始轮廓曲线位置的依赖,新的分割模型采用基于全局凸分割(Globally Convex Segmentation,GCS)方法［13］的实现策略。使用该策略从一个连续的主动轮廓模型出发得到一个离散化的凸分割模型,由于模型本身是凸的,因此最优解不受初始化的影响。在数值实现方面,采用split Bregman迭代算法［14］进行快速求解。

2 局部符号差能量模型

受到局部二值拟合(Local Binary Fitting,LBF)模型［9］的启发,文献［12］提出LSD能量项。令Ω⊂R2为图像的定义域,局部前景聚类和背景聚类可以表示如下:

其中,Ωf,Ωb分别表示轮廓曲线所围成的前景区域和背景区域,核函数Ka,x(y)定义为:

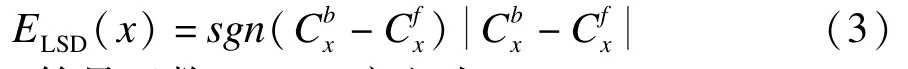
其中,符号函数sgn(x)定义为:

将式(1)代入式(3),可以得到在位置x的像素的LSD能量项如下:

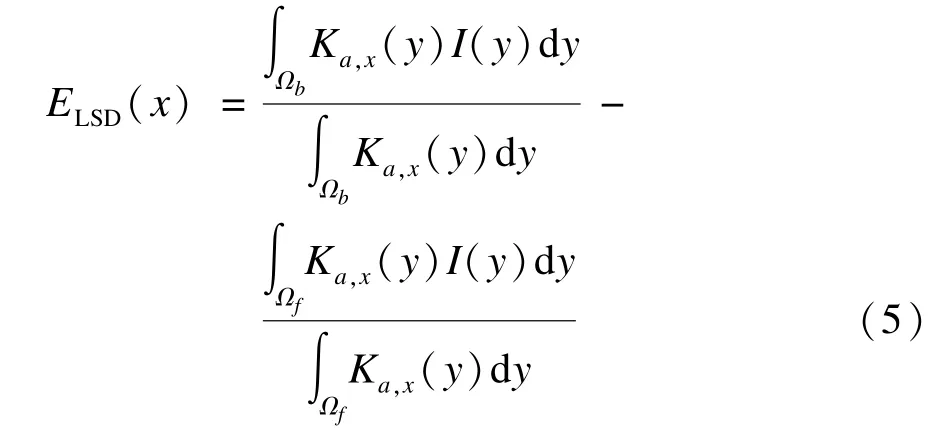
所有LSD局部能量定义为在整个图像定义域内的加权积分:

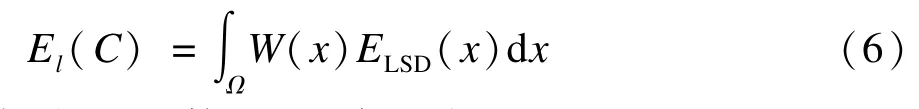
其中,权重函数W(x)定义为:

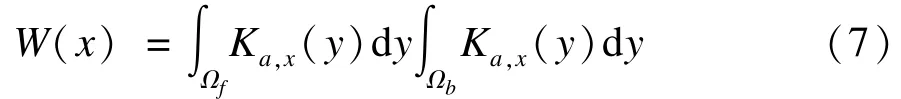
结合式(5)～式(7),整幅图像的LSD能量可以写为:

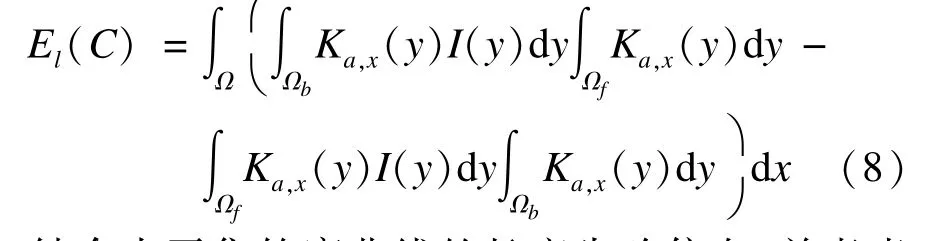
结合水平集轮廓曲线的长度先验信息,并考虑曲线演化过程中水平集函数需要满足符号距离函数(Signed Distance Function,SDF),文献［12］提出的最终能量泛函为:

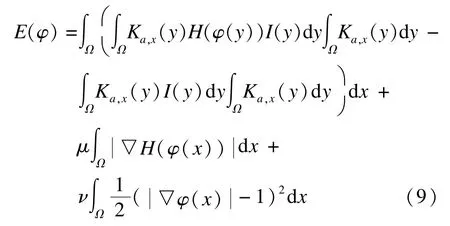
利用梯度下降法对式(9)所表示的能量泛函最小化,可以得到:

其中,外力项F为:

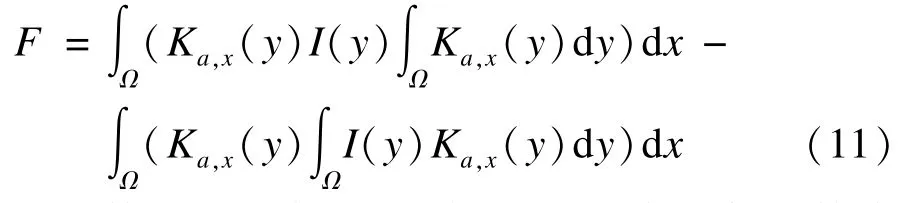
由于外力项F与φ无关,因此在水平集函数演化的过程中仅需计算一次,从而大大提高了算法的运算速度。

3 本文模型

由于传统的主动轮廓模型往往是非凸的,这使得它们很容易陷入局部最优解。图像分割的效果往往和水平集初始轮廓位置的好坏相关。针对这一困难,文献［13］提出了全局凸分割方法,要求能量泛函模型是凸的。由于模型的凸性,使其不受初始轮廓位置的影响而具有全局最优解。除此之外,模型的求解可以采用快速求解策略。最著名一个求解策略就是采用split Bregman迭代求解。文献［14］第一次将split Bregman迭代求解策略应用到图像分割中,从而获得了巨大的成功,其算法运行速度极快。由于文献［14］模型以ACWE模型为基础,因此无法适用非均匀图像的分割问题。本文在LSD模型的基础上结合GCS方法,采用split Bregman迭代求解,既保留了LSD模型的局部分割性,又具有全局凸分割的特性。

为了应用GCS方法,将式(10)中最后一项去掉,令μ=1,方程简化为:

根据GCS方法,式(12)的稳态解等价于下面的简化流方程:

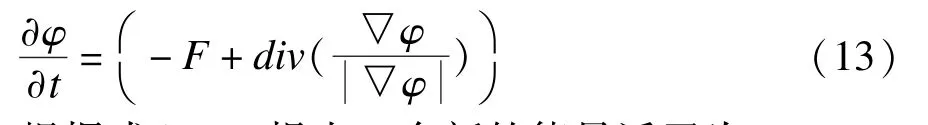
根据式(13),提出一个新的能量泛函为:

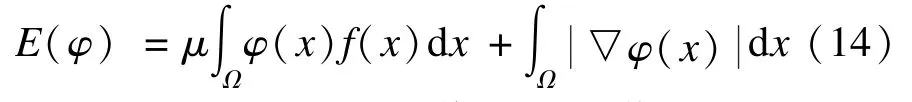
为了增强对非均匀图像的平滑作用,引入MS模型中的光滑项,使分割图像满足分片光滑性。于是,最终能量泛函为:

其中,外力项f(x)为:

为了应用split Bregman迭代算法对式(15)进行求解,将式(15)改写为离散形式式(17),图像分割问题转换为求解函数φ,使得能量泛函E(φ)最小:

可以看出式(17)是凸的。应用split Bregman方法,令dx=▽xφ,dy=▽yφ,得到一个约束优化问题:

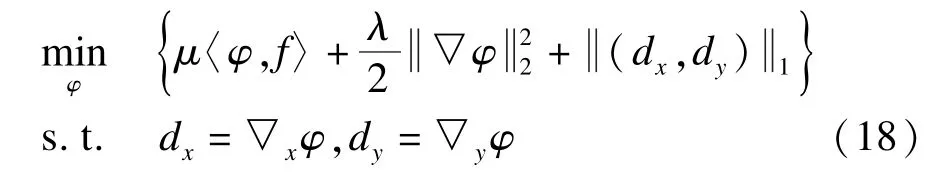
通过将上式转换为无约束优化问题,得到:

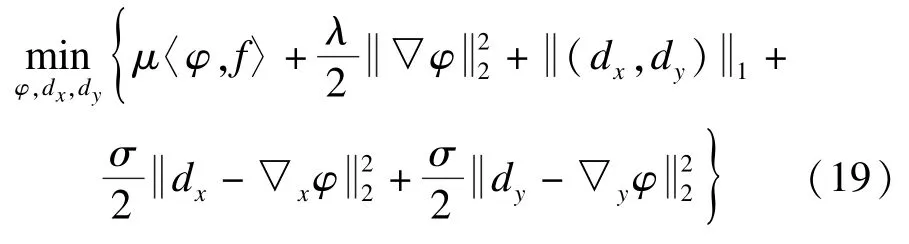
采用split Bregman迭代求解,并且强制约束条件,有:

对式(20)可以通过分别对φ和(dx,dy)进行交替最小化求解。这等价于求解下面2个优化子问题:

对式(23)最小化,其优化条件满足欧拉-拉格朗日(E-L)方程,可以写为:

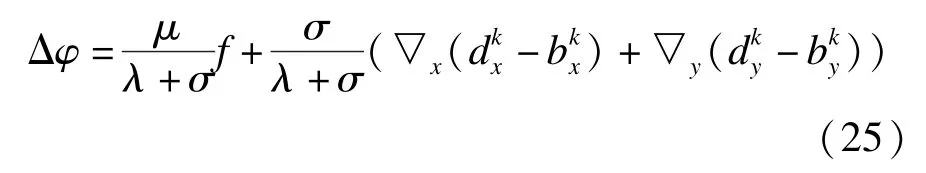
式(24)的最小化可以采用收缩算子式(13)计算得到:

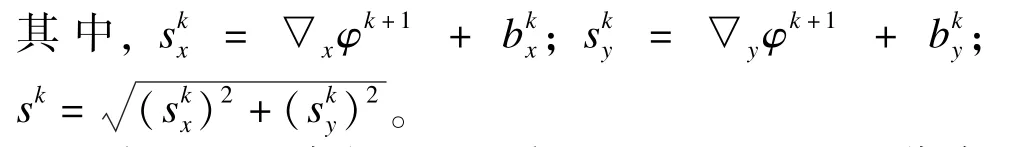
式(25)的求解,可以采用Gauss-Seidel迭代求解,其数值实现如下:

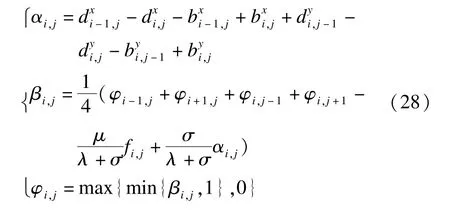
4 实验结果与分析

针对多幅灰度非均匀的真实图像进行了实验比较,用来验证本文模型的可靠性。实验环境为Core2 2.4 GHz CPU,2.00 GB RAM,Matlab 2011b。实验参数的选取除个别图像外,选取统一的参数μ=2,λ=1,σ=1,程序终止的条件为误差ε=10-3。实验一共分为3组:在第1组实验中,针对初始轮廓曲线的位置对图像分割的影响进行比较;在第2组实验中,选取灰度极不均匀、目标明亮差异较大、具有细密纹理的图像进行比较;在第3组实验中,在不同噪声级别下进行分割实验,验证本文模型在噪声干扰存在时的分割效果。

在图1中,选取相同的初始轮廓曲线位置(图中用虚线方框表示)进行比较(除去第2行第1列图像,这是因为若选取和下面相同的初始轮廓曲线位置时,LBF模型无法得到有效的分割结果),较粗的曲线为最终目标边界。

图1 初始轮廓曲线的位置对图像分割的影响

从图1(b)中可以看到,由于初始轮廓曲线的位置设置不当使LBF模型造成了误分割;从图1(c)中可以看到,LSD模型极大改善了这一现象,分割结果受初始轮廓曲线位置的影响较小;从图1(d)可以看出,本文模型在保持LSD模型优点的同时引入了MS模型中的二次平滑项。针对第3幅血管图像,可以看到,本文模型分割结果更加准确。在本组实验中第1幅图像中μ=15;第2幅、第4幅图像中μ=5。

图2中第1幅图像为一幅灰度极不均匀的图像,目标的右下部分几乎和背景一致;第2幅图像为一幅真实的红外图像,目标区域的明暗差异较大;第3幅、第4幅图像为Berkeley数据库中的自然图像,第3幅图像中飞机机身同尾翼具有明显的灰度差,第4幅图像前景和背景区域具有细密的纹理信息。

图2 复杂图像的分割比较

从图2中可以看到,虽然LSD模型受轮廓初始位置的影响较小,但是由于该模型对于目标的灰度具有一定的要求,即目标或者比背景更亮,或者比背景更暗。

由于第1幅图像中目标的右下部和背景的灰度几乎一致,因此无法满足LSD模型对目标灰度的要求,因此分割失败。第2幅图像目标中既包含比背景更亮的部分,也包含比背景更暗的部分,前、背景变化较为复杂,也造成了 LSD模型分割失败。第4幅图像中具有较为细密的纹理信息,这导致LSD模型分割失败。本文模型在实验中得到了较好的分割结果。通过大量实验发现,除了图1、图2中的初始轮廓外,本文模型不受初始轮廓位置的影响,可以随意选取初始轮廓曲线的位置,在本组实验中第1幅图像中μ=30。

表1、表2分别为图1、图2中图像分割运行时间比较,其中,从左至右的4幅图像分别为图像1～图像4。由于本文模型采用误差来控制程序收敛,而水平集模型实现采用迭代次数控制收敛,2类模型实现在迭代次数上没有可比性,因此没有进行相应比较。可以看到,由于LSD模型中符号距离差能量仅需计算一次,因此其运算速度比LBF模型更快。本文模型采用全局凸分割方法,使用split Bregman迭代进行快速求解,驱动力由于采用了LSD能量项,因此也仅需计算一次。可以看到,本文模型同LBF模型、LSD模型相比,其运算速度更快。

表1 图1中各模型迭代次数和运行时间对比

表2 图2中各模型迭代次数和运行时间对比

图3利用本文模型针对不同噪声级别干扰进行相应实验。

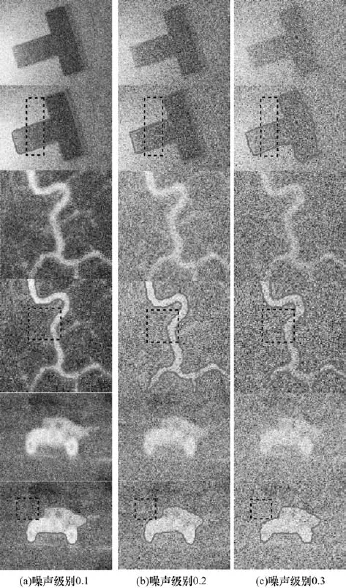
图3 不同噪声等级下的分割结果

图3 中从上到下分别为不同噪声图像及其对应的分割结果。图3(a)在原始图像中添加均值为0、标准差为0.1的高斯白噪声;图3(b)添加了均值为0、标准差为0.2的高斯白噪声;图3(c)添加了均值为0、标准差为0.3的高斯白噪声。从图3可以看到,随噪声等级的提高,图像本身越来越不清晰,其对应的分割效果越来越差。在实验中,仍然选取同前面实验中一致的初始轮廓位置,以验证本文模型的鲁棒性。从图3可以看到,图3(a)虽然存在噪声,但由于噪声级别不高,本文模型仍然获得了较为满意的分割结果。随着噪声的进一步提高,图3(b)本文模型获得的分割结果较图3(a)差,边界也不够光滑,但其分割结果基本可以接受。随着噪声的进一步提高,图3(c)本文模型得到的分割结果最差,边界不够光滑,在一些边界上出现了较大的分割误差,如图3中第2行、第4行中的第3幅分割结果。从实验结果可以看到,在一定噪声范围内,本文模型能够获得较为满意的分割结果,对噪声干扰具有一定的鲁棒性。

5 结束语

本文提出一种新的灰度非均匀图像分割模型。采用LSD能量项作为曲线演化的驱动力,集成了MS模型中的二次光滑项,由于模型本身是凸的,因此可以采用全局凸分割方法,并利用split Bregman迭代算法进行数值求解。实验结果表明,该模型的分割结果不受初始轮廓曲线位置的影响,且具有较强的鲁棒性。然而,本文模型是基于前景、背景两区域分割的模型,今后将进一步研究适用于多区域分割的模型。

［1］高向军.一种向量场卷积外力加速的GAC模型［J］.计算机工程,2012,38(17):192-195.

［2］Gao Xinbo,Wang Bin.A Relay Level Set Method for Automatic Image Segmentation［J］.IEEE Transactions on System,Man and Cybernetics,Part B:Cybernetics, 2011,41(2):518-525.

［3］Zhang Kaihua,Zhang Lei,Song Huihui,et al.Reinitialization Free Level Set Evolution via Reaction Diffusion［J］.IEEE Transactions on Image Processing, 2013,22(1):258-271.

［4］Tony C,Vese L.Active Contours Without Edges［J］.IEEE Transactions on Image Processing,2001,10(2):266-277.

［5］杨名宇,丁 欢,赵 博,等.结合邻域信息的Chan-Vese模型图像分割［J］.计算机辅助设计与图形学学报,2011,23(3):413-418.

［6］Brown E,Tony C,Bresson X.Complete Convex Formulation of the Chan-Vese Image Segmentation Model［J］. International Journal of Computer Vision,2012,98(1): 103-121.

［7］Mumford D,Shah J.OptimalApproximations by Piecewise Smooth Functions and Associated Variational Problems［J］.Communications on Pure and Applied Mathematics,1989,42(5):577-685.

［8］郑 锦,仙 树,李 波.基于形状约束和局部演化的二值水平集运动目标分割［J］.电子与信息学报, 2013,35(5):1037-1043.

［9］Li Chunming,Kao Chiu-Yen,Gore J,et al.Minimization of Region-scalable Fitting Energy for Image Segmentation［J］.IEEE Transactions on Image Processing,2008, 17(10):1940-1949.

［10］Zhang Kaihua,Song Huihui,Zhang Lei.Active Contours Driven by Local Image Fitting Energy［J］.Pattern Recognition,2010,43(4):1199-1206.

［11］林亚忠,李 新,张会奇,等.基于局部特性的分割校正模型改进［J］.计算机工程,2014,40(8):229-232.

［12］Wang Lingfeng,Wu Huaiyu,Pan Chunhong.Region-based Image Segmentation with Local Signed Difference Energy［J］.Pattern Recognition Letters,2013,34(6):637-645.

［13］Tony C,Esedoglu S,Nikolova M.Algorithms for Global MinimizersofImage Segmentation and Denoising Models［J］.SIAM Journal on Applied Mathematics, 2006,66(5):1632-1648.

［14］Goldstein T,Bresson X,Osher S.Geometric Application of the Split Bregman Method Segmentation and Surface Reconstruction［J］.SIAM Journal on Scientific Computing,2010,45(1/3):272-293.

编辑 刘 冰

A New Segmentation Model of Gray Non-uniform Images

WANG Yu1,YAN Mo2
(1.School of Mechanical Engineering,Xi’an Aeronautical University,Xi’an 710077,China;
2.College of Mechanical and Electrical Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,China)

Local region-based Active Contour Model(ACM)is easily influenced by the location of the initial curves when it segments images with intensity inhomogeneity and its numerical implementation based on Level Set(LS)method is lower.For this,a new segmentation model is proposed in this paper.The model includes the Local Signed Difference (LSD)energy as data driven term for curve evolution.In order to reduce the dependence on the location of the initial curve,a Globally Convex Segmentation(GCS)scheme is used to derive a discrete convex segmentation model.The new model includes a second order smooth term from Mumford-Shah segmentation model to make the segmented regions smoother.It uses split Bregman iterations to get a fast numerical implementation.Compared with the Local Binary Fitting (LBF)model,LSD model,experimental results show that the model can segment images with intensity inhomogeneity correctly,and is more efficient and more robust.

image segmentation;local region;gray non-uniform;Active Contour Model(ACM);split Bregman iteration

1000-3428(2015)05-0232-05

A

TP391.06

10.3969/j.issn.1000-3428.2015.05.043

王 瑜(1981-),女,讲师、硕士,主研方向:模式识别,机器视觉;闫 沫,讲师、博士研究生。

2014-11-21

2015-01-03E-mail:wangyu.xh@163.com

中文引用格式:王 瑜,闫 沫.一种新的灰度非均匀图像分割模型［J］.计算机工程,2015,41(5):232-236,242.

英文引用格式:Wang Yu,Yan Mo.A New Segmentation Model of Gray Non-uniform Images［J］.Computer Engineering, 2015,41(5):232-236,242.