基于响应面法的转向驱动桥空心半轴轻量化优化设计*

汪朝晖,朱发渊,吕 密,陈 思

(1.武汉科技大学机械自动化学院，武汉 430081；2. 重庆建设工业(集团)有限责任公司，重庆 400054)



2015248

基于响应面法的转向驱动桥空心半轴轻量化优化设计*

汪朝晖1,朱发渊1,吕 密2,陈 思1

(1.武汉科技大学机械自动化学院，武汉 430081；2. 重庆建设工业(集团)有限责任公司，重庆 400054)

提出了一种基于数值优化与有限元模拟相结合的汽车转向驱动桥空心半轴轻量化设计方法。以半轴各段的壁厚、长度和过渡角为设计变量，半轴质量最小化为优化目标，2阶约束模态频率和半轴花键末端圆角过渡处等效应力为约束条件，建立了半轴轻量优化模型。利用正交试验设计得到10个设计变量和3个水平的数值模拟试验组合。采用最小二乘法建立了响应面近似模型，并利用序列二次规划算法对模型进行了迭代优化。结果表明：轻量化优化后的变径全空心半轴质量比初始设计减少约16.7g，半轴2阶约束模态频率增加约0.6Hz，且半轴花键末端圆角过渡处和最小轴径处的等效应力值均低于半轴材料的抗扭强度。

空心半轴;轻量化设计;正交试验设计;最小二乘法;响应面模型

前言

汽车轻量化设计是节约能源消耗的重要途径，研究表明：汽车运动部件质量每减轻1%，则可节油2%[1]。转向驱动桥半轴是汽车最重要的运动零部件之一，它对汽车的驱动性能和运行稳定性有重要影响。传统的转向驱动桥半轴结构轻量化优化设计主要是依据工程经验，其试验研究难度较大，设计周期冗长。因此，采用新的轻量化优化方法设计转向驱动桥半轴势在必行。

国内外诸多学者在保证汽车传动轴工作可靠的基础上引入材料低载强化特性获取新型传动轴结构，取得了较好效果。文献[2]中以材料40Cr的低载强化特性为依据，设计出空心传动轴，并对轻量化的传动轴进行强度校核及模态对比分析，验证了设计可行性；文献[3]中在传动轴结构优化过程中，以最佳累积强化效果为目标，根据设计应力分布区间与结构低载强化特性区间的对应关系获取了结构尺寸参数，验证了结构轻量化设计的有效性。但以上传动轴轻量化设计并不是轴类零部件最优化结构，其空心传动轴内径值不变，在一定程度上没有达到节约材料的目的。

国内外学者通常是寻找合适的替代模型来对具体的工程问题进行优化。文献[4]中在白车身开发早期引入结构轻量化思想，建立隐式全参数化白车身优化设计近似模型，通过多学科优化获取了白车身零件形状、尺寸、位置与厚度等各参数之间的最佳组合；文献[5]中选择拉丁超立方试验抽样数据，并在考虑多变量和处理近似误差的基础上，使用稀疏响应面法评估各种结构机械的可靠性；文献[6]中利用基于移动最小二乘的响应面法建立了机械结构可靠性分析的近似模型，结果表明：对于随机变量其基于移动最小二乘的近似响应面函数更加高效和准确。

本文中以当前利用材料低载强化特性理论自主研发的新型转向驱动桥变径空心半轴作为进一步轻量化设计对象，将数值优化方法与有限元模拟技术相结合，利用正交试验设计得到试验样本数据，通过最小二乘法对试验设计数据进行拟合，获取具有较好预测精度的半轴轻量化的近似模型，并采用序列响应面优化方法对近似模型进行优化。本文中通过改变空心半轴的径向厚度、缩径段长度及其过渡角，寻找一组合适的半轴管参数，使空心半轴在满足汽车驱动性能和稳定性的前提下质量最小，研究结果可为汽车驱动系统半轴及其相关零部件的轻量化优化设计理论及方法奠定基础。

1 基于响应面法的优化方法

1.1 二次响应面近似模型

工程实践的大部分优化设计问题中，其目标函数与设计变量之间的函数关系是未知的。而以试验设计为基础的统计处理技术-响应面法(response surface method,RSM)可较精确地建立目标函数与设计变量之间的近似数学预测模型[7]。

2阶多项式响应面近似模型具有良好的连续性和可导性，具有易于实现快速寻优等特点，因而在工程实际中得到广泛应用[8]。本文中采用的近似模型为

(1)

式中：n为设计变量数;xi和xj为第i和第j个设计变量；βi，βii和βij为回归系数；ε为误差项。

其矩阵形式为

Y=βX+λ

(2)

式中：X为设计变量矩阵；Y为试验实际响应矩阵；β为回归系数矩阵；λ为误差项矩阵。

设b=[b1,b2,…,bk]T为β=[β1,β2,…,βk]T的最小二乘估计，由最小二乘法可知，[b1,b2,…,bk]T应使全部观察值yi与回归值yi1的偏差平方和Q达到最小。

(3)

由微积分学的极值定理可知，b=[b1, b2,…, bk]T应是式(4)方程组的解，解方程组即可得到式(5)所示的多项式系数的无偏估计[9]。

(4)

b=(XTX)-1XTY

(5)

式中：b0和bj分别为回归系数β0和βj的无偏估计；b为回归系数的无偏估计矩阵；X为设计变量矩阵；Y为试验实际响应矩阵。

1.2 序列二次规划优化算法

序列二次规划算法源于拟牛顿法，是最简单的约束非线性规划算法[10]，工程上常见的具有不等式约束的非线性规划问题一般表示为

(6)

序列二次规划的原理为在当前的迭代点xk处作泰勒展开，将目标函数的二次近似及约束函数的一次近似构成一个如式(7)所示的子二次规划问题，然后通过求解这个二次规划获得下一迭代点xk+1。

(7)

式中：k为迭代次数；dk为第k次迭代的优化搜索方向；Bk是正定矩阵，初始化时为单位矩阵。解式(7)所示的子二次规划问题，得到的dk就是搜索方向，沿搜索方向进行一维搜索，确定步长ak，然后按式(8)的格式进行迭代，最终得到非线性约束问题的最优解[11]。

xk+1=xk+akdk

(8)

2 正交试验设计

试验设计是构建响应面近似模型必不可少的环节，其主要作用是研究设计参数对响应的影响。由于全面试验空间巨大，导致数值模拟和优化迭代时间很长，因此，须要在整个设计空间选取有限数量能尽可能反映设计空间特性的样本点，以提高运算效率。

正交试验设计是研究和处理多因素试验的一种科学的方法，其思想是均匀分散和整齐可比，以减少试验次数，提高试验精度[12]。首先，利用合理的正交表安排少量试验，获得反映全面试验的分析信息；其次，采用方差分析等数理统计方法对试验分析结果进行处理，从多个因素中获得主、次要因素及其对试验的影响规律，得到更为科学和合理的结论。

由图1 所示的三因素三水平试验的立体图可以看出，采用正交表安排的试验，具有均衡分散、整齐可比、代表性强和效率高的特点。

3 半轴轻量化优化模型

由半轴使用经验和轻量化的多学科优化问题可知，在半轴结构安全设计学科中主要考虑其在使用过程中承受着较大的交变载荷，其结构必须具有足够的静强度和刚度来满足其疲劳寿命、装配和使用的要求。另外，半轴的低阶模态振型是其能否正常工作的重要性能之一，必须有合理的动态特性来达到控制振动与噪声的目的。

文献[13]中对变径空心半轴的研究表明：半轴的1阶约束模态为刚体模态，真正意义上的约束模态是从第2阶模态振型开始的。因此，本文中考虑以空心半轴端花键圆角过渡处等效应力、半轴2阶约束模态和半轴质量为设计响应，其轻量化优化设计问题的数学模型可表示为

(9)

式中：m(d)为半轴质量；fq为半轴的2阶约束模态值；[f]为半轴的2阶约束模态许用极限；σr为半轴在满载工况下的最大应力值；[σ]为半轴在满载工况下的许用强度极限；d为设计变量矩阵。

采用上述有限元数值模拟和响应面建模相结合的方法，在不改变图2所示的变径空心半轴材料及外形尺寸的前提下对其进行轻量化优化设计。

变径空心半轴材料为34MnB5，标准为DIN 10305-2，编号为1.1166，等级为N级，试验测得半轴材料34MnB5的相关特性参数如表1所示。

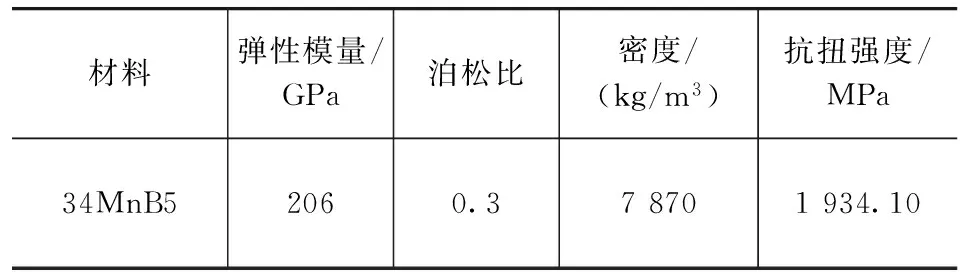
表1 材料特性参数

4 半轴轻量化优化计算

4.1 试验方案

对于本文中空心半轴轻量化优化问题，考虑到半轴使用经验和前期的数值模拟结果，最终选用10个设计变量，每个变量取3个水平，得到如表2所示的数值模拟试验组合。考虑到正交表的选用规则，选用L27(311)正交表来安排数值模拟试验，留有1空列作为试验误差衡量试验的可靠性。

表2 数值模拟试验因子及其水平

4.2 数值模拟结果分析

变径空心半轴的三维有限元模型如图3所示，其中图3(a)为整轴模型，图3(b)为轴端模型。由于轴端花键齿部位结构较不规则，故采用10节点的四面体单元，半轴其他规则部位则采用20节点的六面体单元；在极限载荷下的半轴静态有限元模型节点个数为152 738，单元数为103 258；在约束下的模态分析有限元模型节点个数为46 220，单元数为27 574。因半轴内端花键与三销式滑移节连接确保其能沿轴向移动，故本文中约束空心半轴内端花键节点的5个自由度。在其空心半轴外端施加极限转矩Tmax=3 700 N·m，转矩载荷加载于花键处，加载位置为花键的单侧斜面。

在对试验结果进行方差分析时，如果误差自由度(dfe)很小，F检验灵敏度很低，即使因素对试验指标有影响，用F检验也判断不出来[13]。本文中为了增大误差自由度，提高F检验灵敏度，在进行显著性检验之前，先比较各因素方差与误差方差，若MSf小于2MSf，将这些因素的偏差平方和与自由度并入误差的偏差平方和与自由度，使误差的偏差平方和与自由度增大，从而提高F检验的灵敏度。

半轴质量响应的方差分析如表3所示。由分析结果可知：T6和L2的F值分别为12.504和19.731，大于F0.01(2，16)=6.23，对目标函数的影响高度显著；T2和α1的F值分别为4.480和6.004，大于F0.05(2，16)=3.63，对目标函数的影响显著；T7的F值为3.127，大于F0.1(2，16)=2.67，对目标函数的影响比较显著。其余设计变量对目标函数的影响很小，基本可以忽略。因此，经过方差分析，筛选出T6，L2，T2，α1和T7作为设计变量，构建轻量化优化设计的数学模型，半轴轻量化优化设计的规模将很大程度上得到减小。

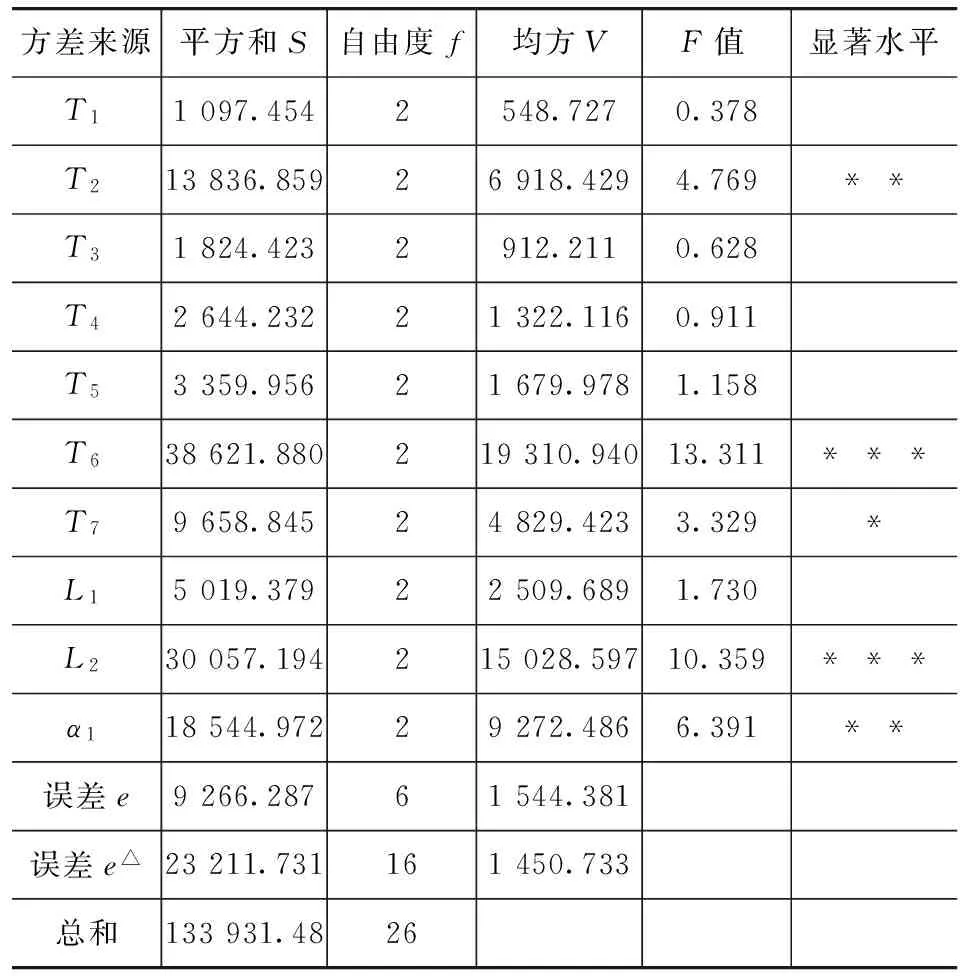
表3 半轴质量响应方差分析结果

4.3 响应面预测模型与优化

运用本文中提出的轻量化优化设计方法，建立了变径空心半轴质量m的响应面近似模型：

m=(10.1239+0.0105T2-0.6737T6-0.0298T7-

0.016172L2+0.0588α1+0.8651T2T6+0.6604T2T7+

0.5691T6T7-0.0340T2L2-0.0293T7L2-0.1630T2α1+

0.2794T6α1+0.3008T7α1+0.0039L2α1-0.0349T22+

3.9167T62-1.6042T72)×103

(10)

方差分析检验了多项式响应面的精度，其R2为0.951，Ra2为0.979。由此可知，该二次多项式响应面近似模型的拟合精度较好，能精确反映目标函数与设计变量之间的数学关系，可用它来替代物理有限元模型。利用序列二次规划算法(SQP)对上述多项式响应面近似模型进行迭代优化计算，整个优化过程仅需4次迭代就可收敛并得到最优解，优化前后半轴设计变量及其响应的初始值和优化值见表4。

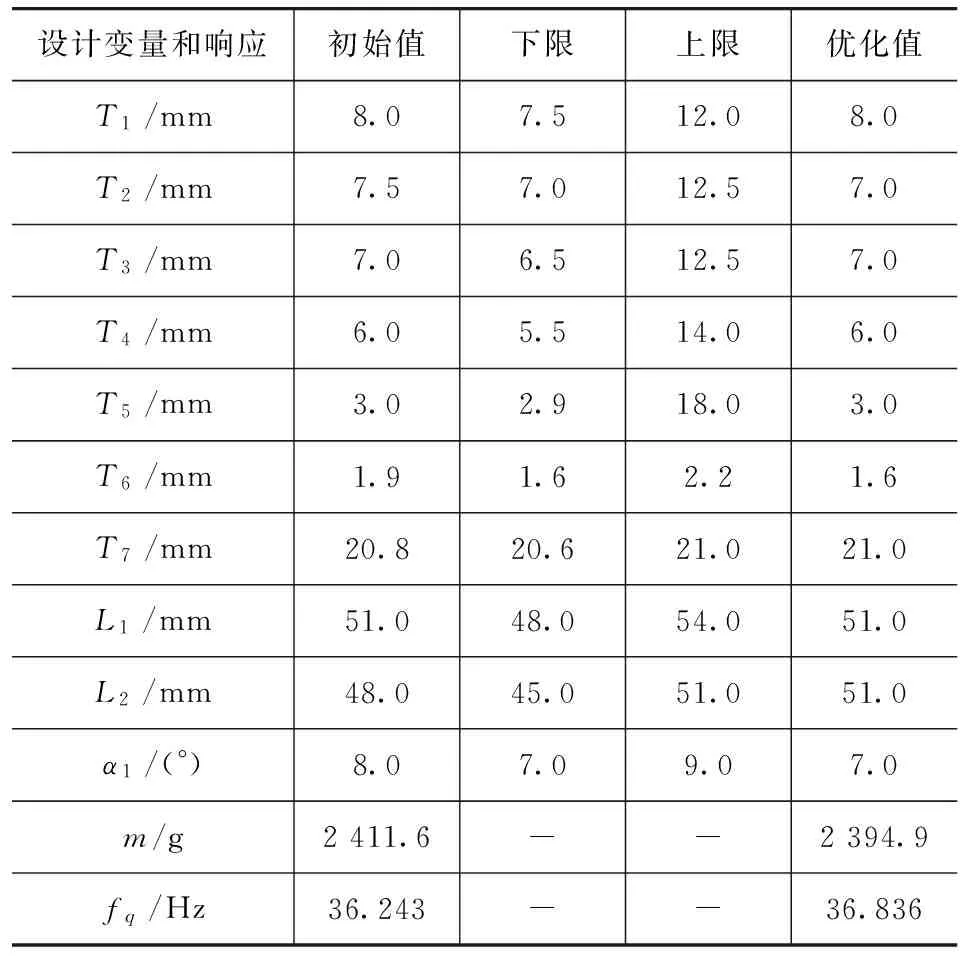
表4 设计变量和响应值的初始值和优化值

由表4可知，通过对采用最小二乘拟合得到的半轴质量多项式响应面近似模型进行优化，使半轴质量比初始设计时减少约16.7g，较好地降低了半轴的质量，它将对汽车的节能减排起到较为重要的作用；半轴的2阶约束模态值增加了约0.6Hz，这将一定程度上改善汽车的乘坐舒适性能和平顺性能。

新型轻量化优化设计的半轴在极限转矩下的等效应力云图如图4所示，等效应力最大值发生在一小部分半轴花键圆角过渡处，等效应力大于1 500MPa的范围很小，基本集中在花键圆角过渡部位。这是由于半轴在传递工作转矩时，各花键齿近似受到单侧均布载荷，所以在靠近半轴端面的键齿齿面应力较小，齿形截面通过圆角过渡到光轴圆截面，引起应力局部增大。但由于花键自身齿数较多，键齿受力均匀，所以圆角过渡处应力梯度较小。半轴花键末端圆角过渡处和最小轴径处的等效应力值均低于半轴材料的抗扭强度1 934.10MPa，新型轻量化优化设计的半轴满足强度设计要求。

5 结论

在满足综合机械性能的前提下，为获得质量较小的转向驱动桥变径空心半轴，提出并建立了一种基于有限元数值模拟和近似响应面法的半轴轻量化优化设计方法。

(1)采用正交试验设计采集数值模拟数据，基于最小二乘拟合法建立多项式响应面近似模型，并将其引入到半轴轻量化优化设计中，可以较为准确地描述设计变量与设计目标之间的关系。

(2)在较好地满足静态扭转刚度和强度要求下，建立了变径空心半轴轻量化优化设计的响应面近似模型，运用该多项式响应面近似模型进行优化计算，并结合序列二次规划优化算法分析了半轴管参数对半轴质量的影响。

(3)在满足半轴工作安全性设计的同时，较好地达到了半轴质量较小的优化目标，缩短了优化设计周期，并且相对于原半轴结构，左右两半轴的频率较好地达到一致，有效提升了整车舒适性。

[1] Reginald T. Trends in Automotive Light Weighting[J]. Metal Finishing, 2013, 111(2): 23-25.

[2] Zheng S L, Xu H H, Feng J Z, et al. Lightweight Design of Automobile Drive Shaft Based on the Characteristics of Low Amplitude Load Strengthening[J]. Chinese Journal of Mechanical Engineering, 2011, 24(6): 1111-1114.

[3] 储军, 郑松林, 冯金芝, 等. 基于低幅锻炼载荷的累积强化效果模型[J]. 机械工程学报, 2011, 47(16): 30-34.

[4] 史国宏, 陈勇, 杨雨泽, 等. 白车身多学科轻量化优化设计应用[J]. 机械工程学报, 2012, 48(8): 110-114.

[5] Roussouly N, Petitjean F, Salaun M. A New Adaptive Response Surface Method for Reliability Analysis[J]. Probabilistic Engineer Mechanics, 2013, 32(4): 103-115.

[6] Kang S C, Koh H M, Choo J F. An Efficient Response Surface Method Using Moving Least Squares Approximation for Structural Reliability Analysis[J]. Probabilistic Engineer Mechanics, 2010, 25(4): 365-371.

[7] Zhao W T, Qiu Z P. An Efficient Response Surface Method and Its Application to Structural Reliability and Reliability-based Optimization[J]. Finite Elements in Analysis and Design, 2013, 67(5): 34-42.

[8] Ye L, Yang M, Xu L, et al. Optimization of Inductive Angle Sensor Using Response Surface Methodology and Finite Element Method[J]. Measurement,2014, 48(2): 252-262.

[9] Allaix D, Carbone V. An Improvement of the Response Surface Method[J]. Structural Safety, 2011, 33(2): 165-172.

[10] 徐敬华, 张树有, 沈炜良. 基于序列二次规划的动态可局部称重方法[J]. 中国机械工程, 2009, 20(8): 892-895.

[11] Guo C H, Bai Y Q, Jian J B. An Improved Sequential Quadratic Programming Algorithm for Solving General Nonlinear Programming Problems[J]. Journal of Mathematical Analysis and Applications, 2014, 409(2): 777-789.

[12] 王平, 郑松林, 吴光强. 基于协同优化和多目标遗传算法的车身结构多学科优化设计[J]. 机械工程学报, 2011, 47(2): 102-108.

[13] Joardar H, Das N S, Sutradhar G, et al. Application of Response Surface Methodology for Determining Cutting Force Model in Turning of LM6/SiCPMetal Matrix Composite[J]. Measurement, 2014, 47(1): 452-464.

Lightweight Optimization Design of the Hollow Half Shaft of Steering Drive Axles Based on Response Surface Method

Wang Zhaohui1, Zhu Fayuan1, Lü Mi2& Chen Si1

1.CollegeofMechanicalEngineering,WuhanUniversityofScienceandTechnology,Wuhan430081;2.ChongqingConstructionIndustrial(Group)Co.,Ltd.,Chongqing400054

A lightweight design method is proposed for the hollow half shaft of a vehicle steering drive axle based on the combination of numerical optimization and finite element simulation. An optimization model for the lightweighting of half shaft is set up with the thicknesses and lengths of different parts and the transitional angle of half shaft as design variables, minimizing the mass of half shaft as optimization objective, and the 2ndorder constrained mode frequency and the equivalent stress at the filleted corner of spline end as constraints. A numerical simulation experiment combination of ten design variables with three levels each is determined by using orthogonal experimental design, a response surface approximation model for the half shaft is established by using least squares method, and an iteration optimization is conducted on the model with sequential quadratic programming algorithm. The results show that after lightweighting optimization the mass of hollow half shaft reduces by 16.7g, the frequency of 2ndorder constrained mode increases by 0.6Hz, and the equivalent stresses at both the filleted corner of spline end and the location with smallest diameter are lower than the torsional strength of half shaft material.

hollow half shaft; lightweight design; orthogonal experimental design; least square method; response surface model

*重庆市科技攻关计划项目(CSTC2014YYKFB0187)和武汉科技大学研究生创新创业基金(JCX0018)资助。

原稿收到日期为2014年5月8日，修改稿收到日期为2014年8月21日。