汽车轮胎性能矛盾相容的新非自然平衡轮廓设计的研究*

杨 建,王国林,万治君

(江苏大学汽车与交通工程学院风神江大车轮研究所，镇江 212013)



2015239

汽车轮胎性能矛盾相容的新非自然平衡轮廓设计的研究*

杨 建,王国林,万治君

(江苏大学汽车与交通工程学院风神江大车轮研究所，镇江 212013)

在酒井秀男和Frank非自然平衡轮廓设计理论的基础上，提出了新的充气轮胎非自然平衡轮廓积分方程。采用不同理论对11.00R20和385/65R22.5两种规格载重车子午线轮胎进行胎体轮廓设计。利用ABAQUS软件从轮胎磨损、滚动阻力和抓地力等方面，对采用3种不同轮廓理论设计的两种规格轮胎的性能进行对比分析，并与现行设计轮胎的性能进行对比。结果表明，Frank非平衡轮廓设计理论有利于提升轮胎磨损性能；酒井秀男非平衡轮廓设计理论有利于降低轮胎滚动阻力和提高轮胎抓地力；而新非自然平衡轮廓设计理论则可提升轮胎的整体性能，解决了轮胎不同性能间相互矛盾的难题。与现行设计轮胎相比，新非自然平衡轮廓理论设计的轮胎，在减小磨损、降低滚动阻力的同时提高了轮胎的抓地力。

轮胎；轮廓设计；非自然平衡轮廓理论；矛盾性能

前言

据统计，2013年我国轮胎产量达9.65亿条，成为轮胎生产第一大国。但与国外品牌相比，国内生产的轮胎品质仍存在较大差距。此外，许多国家和地区相继出台了轮胎标签法规，对轮胎安全、燃油消耗和绿色环保性能等提出了明确要求和实施期限[1]。但目前我国生产的轮胎尚不能完全达到标签法的要求[2]。因此，亟须对轮胎产业进行转型升级，提升轮胎产品的竞争力。

为提升轮胎性能，国内外学者从橡胶配方[3-5]、花纹结构[6-11]和胎体轮廓[12-13]等方面开展了大量的研究。然而，汽车轮胎性能间存在诸多不相容的矛盾，如耐磨性、滚动阻力和抓地力是轮胎最主要的性能，但这三者间相互制约且矛盾突出，三者的关系被称为“魔鬼三角”[14]，即提升轮胎的某一性能将会降低其它性能。如胶料配方中添加白炭黑或硅在提升轮胎抓地性能的同时会降低胎面胶的耐磨性能[4]；减小接地区橡胶变形可降低滚动阻力，但同时也会降低接地区橡胶与地面的仿形能力，降低了轮胎的抓地性能[8-9]。上述研究已证明胶料配方、花纹结构和胎体轮廓等直接影响轮胎的磨损、滚动阻力和抓地力等性能，但以往研究只针对轮胎的单一性能，很少考虑轮胎多性能间的相互影响，未能解决轮胎性能间的不相容性难题。

本文中融合了酒井秀男和Frank非自然平衡轮廓设计理论的特点，提出新的轮胎充气非自然平衡胎体轮廓积分方程。以11.00R20和385/65R22.5两种规格载重子午线轮胎为研究对象，利用3种非自然平衡轮廓理论对其进行胎体轮廓设计。利用ABAQUS软件，从轮胎磨损、滚动阻力和抓地力方面对2种规格3种不同轮廓理论设计的轮胎性能进行研究，并与现行设计的轮胎性能进行对比分析。为从胎体轮廓设计角度突破轮胎性能间的不相容性难题提供设计依据和理论指导。

1 子午线轮胎的非自然平衡轮廓设计

1.1 轮胎的新非自然平衡轮廓理论

胎体轮廓形状直接决定其内部受力和行驶状态，从而影响轮胎磨损、安全性和滚动阻力等一系列性能指标。以往的轮胎轮廓设计采用自然平衡轮廓法，即假设轮胎充气后轮廓不变，且胎体帘布层所受张力呈均匀分布，但该理论不能充分模拟轮胎的使用状态。非自然平衡轮廓理论的提出为高性能轮胎轮廓设计提供了指导，对提升轮胎性能具有实际意义[15]。

诸多非自然平衡轮廓理论之一的提出者酒井秀男考虑了带束层和加强层结构对轮胎轮廓的影响，并提出压力分担率的概念，认为在胎冠和下胎侧部位，轮胎的内压并非完全由胎体帘布承担，相反大部分的压力是由带束层和加强层承担[16]。Böhm和Frank基于薄膜-网格理论对子午线轮胎断面形状进行了研究，提出轮胎断面主曲率半径是以带束层角度、胎体帘线角度、断面最宽点半径和带束层压力分担率为参数，以半径和径向角为函数的表达式；Frank认为胎体与带束层之间的压力分担率按梯形曲线分布比抛物线更接近实际，且压力分担率在带束层宽度区域内可近似地看为常数[17]。结合酒井秀男和Frank非自然平衡轮廓理论的特点，文献[18]中对2种理论进行了有效的融合修正，并利用有限元方法证实了在带束层宽度范围内带束层压力分担率近似为常数，同时考虑到充气状态下轮胎下胎侧的加强层对胎体压力分担的作用不可忽视，在此基础上，提出了新的轮胎充气非自然平衡轮廓的积分方程，即胎冠部位轮廓曲线由Frank提出的曲线方程求得，胎侧中间部位和下胎侧部位的轮廓曲线由酒井秀男提出的曲线方程求得，并用轮胎断面宽度ym作为中间量将2种理论融合修正。子午线轮胎断面轮廓曲线如图1所示。

各部分轮廓曲线的计算公式如下：

(1)

式中：yd为带束层宽度；rd为带束层端点至旋转轴半径；rm为轮胎最宽点至旋转轴半径；rk为胎冠点至旋转轴半径；ζ=1-τ0，τ0为带束层压力分担率；ym为轮胎断面宽度；r为轮廓点至旋转轴的距离；a为带束层压力分担率形状系数。

(2) 胎侧中间部位(图1中D-E区间)

(2)

(3) 下胎侧部位(图1中E-B区间)

(3)

其中

式中：re为加强层上端至旋转轴半径；rb为胎圈中心至旋转轴半径；τe为加强层压力分担率。通过对式(1)～式(3)积分可得胎体轮廓曲线。

1.2 胎体轮廓曲线绘制

当已知轮胎胎体轮廓关键设计参数ym,rd,rk,re,rb,τ0和τe时，利用式(1)～式(3)积分方程可得胎体轮廓曲线；同时利用专用软件可方便、准确地绘制出任意规格的子午胎的非自然平衡胎体轮廓曲线[18]，如图2所示。

1.3 轮胎的非自然平衡轮廓绘制与对比

本文中从窄基轮胎(高扁平比)和宽基轮胎(低扁平比)中分别选择11.00R20和385/65R22.5进行胎体轮廓设计，并将2种规格的3种不同非平衡轮廓设计的胎体轮廓与现行设计轮胎的胎体轮廓进行对比分析，其轮胎胎体轮廓关键设计参数如表1所示(新非自然平衡轮廓理论设计简称新设计)。

根据表1的设计参数，利用本文中编制的专用软件绘制了2种规格轮胎所对应的3种非平衡轮廓设计的胎体轮廓曲线，并与现行设计轮胎轮廓曲线进行了对比，如图3所示。

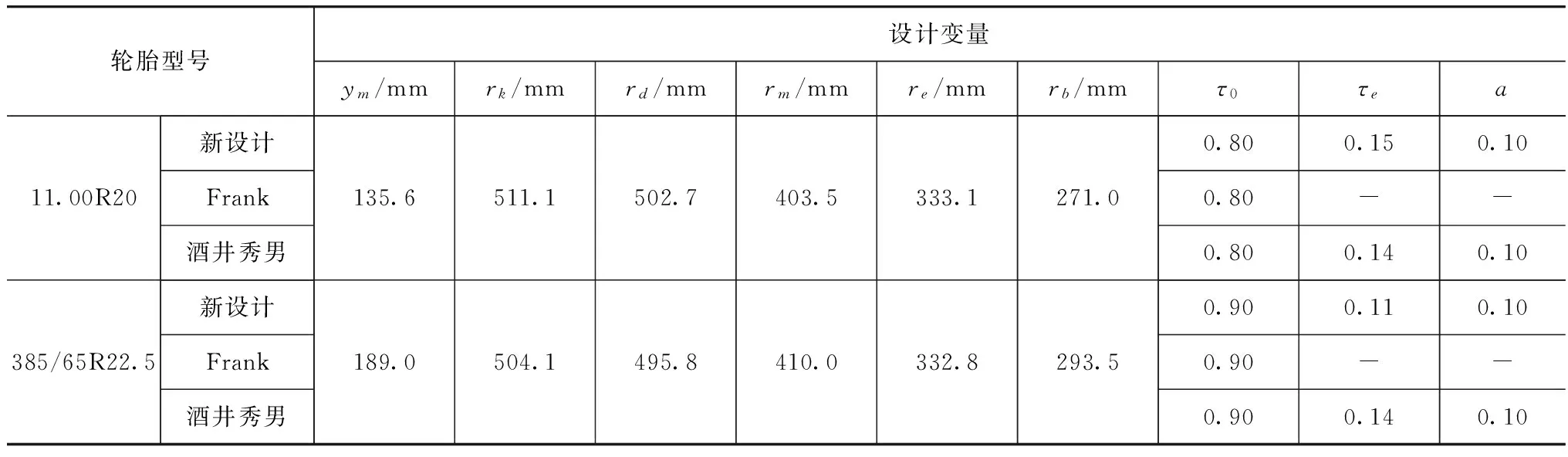
表1 胎体轮廓的关键设计参数

由图3可以看出，对11.00R20轮胎而言，现行设计轮胎轮廓与酒井秀男设计轮胎胎体轮廓基本重合，只在胎圈部位稍有差异；依据酒井秀男和Frank的非平衡轮廓理论设计的胎体轮廓曲线整体较为相似，胎冠弧和胎侧部分基本重合；但在下胎侧区域，由于Frank的设计理论没有考虑加强层的作用，所以当充气压力完全由胎体承担时，将导致轮廓曲线向内凹陷且轮胎的子口宽度得不到有效控制；新非自然平衡轮廓理论设计的轮廓曲线与其他轮廓曲线相比差别较大，其胎面曲线更平坦，胎肩曲率更大，胎侧曲线更平直，从而增加了胎侧的长度。对385/65R22.5轮胎而言，3种非平衡轮廓理论设计的胎体轮廓各不相同。现行设计轮胎轮廓与Frank设计轮廓基本重合，只在胎圈部位稍有差异；在水平轴以上部位，新非自然平衡轮廓理论设计、Frank理论设计和现行设计的胎面曲线均较为平坦，新非平衡轮廓设计的轮廓曲线，其胎肩曲率更大，胎侧曲线更平直；酒井秀男设计的轮廓，其胎面弧度与胎侧曲率均较大，从而缩短了胎侧的长度。

2 不同轮廓理论设计的轮胎性能分析

将图3中2种规格4种轮廓设计的胎体轮廓曲线导入CAD中，根据轮胎设计标准，采用较为普遍的“3+0°”带束层结构，设计轮胎的材料分布图。本文中对Frank理论的设计弊端做了适当处理，在胎圈部位采用现行设计进行替代，且考虑到制造成本和变量控制，外轮廓和胎面轮廓均采用现行设计，其各断面材料分布如图4所示。

由于轮胎磨损、滚动阻力和抓地力均与轮胎的接地特性相关，所以本文中利用图4的轮胎断面材料分布图建立有限元模型，其中橡胶部分采用CGAX3H与CGAX4H单元模拟；轮胎钢丝帘线采用SFMGAX1单元模拟；轮辋和路面定义为解析刚体；同时考虑路面与胎面和胎圈与轮辋之间的摩擦。利用ABAQUS软件对轮胎的磨损、滚动阻力和抓地力进行数值分析，探索不同理论设计的轮廓对轮胎性能的影响规律。

2.1 轮胎静态接地压力分布试验

为验证所建有限元模型的有效性，采用T-SCAN型轮胎接地压力分析系统，分别对11.00R20和385/65R22.5现行设计轮胎进行了接地压力分布试验，有限元分析与试验测试结果如图5所示。

由图5可知，无论是接地形状还是接地压力分布，有限元分析结果和试验结果表现出了良好的一致性，说明本文中所建的有限元分析模型具有较高的精度。

2.2 磨损性能有限元分析

2.2.1 轮胎接地区摩擦功计算方法

由于橡胶的黏弹特性，轮胎与路面在接触过程中，不可避免地存在能量损耗。当只考虑摩擦的影响和胎面变形时，能量耗散E的计算公式[19]为

(4)

其中s=xi+yj

(5)

式中：τ为胎面接地点切向力；s为轮胎胎面接地点位移；l为轮胎接地印痕长度。文献[19]中验证了该计算方法的准确性。

当轮胎处于纵滑状态时，y=0，则：

s=x

(6)

考虑轮胎胎面在黏着区的变形，由式(4)可得接地点能量耗散为

(7)

式中：x1为滑移区滑移起始点的横坐标；τa为黏着区内一点的切向力；S为滑移率；μ为轮胎与路面的摩擦因数；P(x)为滑移区接地点接地压力。

2.2.2 边界条件设定

当轮胎自由滚动时，其与路面处于黏着状态，存在微小滑移，轮胎产生很小的磨损；当轮胎处于制动或驱动状态时，轮胎与路面处于相对滑动和黏着的双重状态，轮胎会产生磨损。文献[20]中指出轮胎自由滚动工况的发生频率为80%，为轮胎磨损的主要贡献者。因此，可通过计算2种规格4种轮廓设计的轮胎自由滚动时接地面的摩擦能量损失来比较它们的磨损性能，边界条件设定如表2所示，其中滑移率的选取参照文献[20]。

表2 轮胎磨损的边界条件设定

2.2.3 仿真结果分析

2种规格4种不同轮廓设计的轮胎在自由滚动过程中的摩擦能量损失如表3所示。

表3 轮胎摩擦能量损失

由表3可知，对不同规格的轮胎，3种非平衡轮廓设计的轮胎的摩擦能量损失呈现相同的变化趋势，酒井秀男非平衡轮廓轮胎的摩擦能量损失最大，新非平衡轮廓轮胎的摩擦能量损失最小。与酒井秀男和Frank非平衡轮廓轮胎相比，新非平衡轮廓设计的11.00R20轮胎摩擦能量损失分别降低了7.08%和3.57%；新非平衡轮廓设计的385/65R22.5轮胎摩擦能量损失则分别降低了44.74%和22.55%。这是由于新非自然平衡轮廓设计的轮胎具有平坦的胎面轮廓和近似平直的胎侧，从而减小了胎肩厚度，可有效抑制由于胎肩增厚生热量过高、散热困难造成胎肩开裂和轮胎使用寿命降低的情况。另外，趋于平直的胎侧，在充气过程中通过胎体的变形能有效抑制胎肩处的膨胀，从而避免接地过程中胎肩处的应力集中，使轮胎的接地压力分布更加均匀，防止出现胎肩偏磨现象。385/65R22.5轮胎与地面摩擦能量损失比11.00R20轮胎低，这是由于前者具有更大的接地面积，在相同负荷的情况下，接地压力较小，致使产生滑移的区域也较后者小。

图6为2种规格4种不同轮廓设计的轮胎的摩擦功分布。由图6可知，轮胎自由滚动时，接地面摩擦功分布主要集中在轮胎接地区前、后端的胎肩处，并非轮胎接地压力较大的胎面中心处，并且沿着滚动方向，前端比后端略大，这是由于滚动阻力的存在使轮胎的接地中心略往前进方向移动，从而使接地面前进方向的前端产生的滑移量较其它部位要大。由此可以看出，轮胎自由滚动时，接地能量损耗不仅与接地压力有关，而且与接地区橡胶的滑移距离有关，故不能简单地认为轮胎接地压力越大，轮胎的摩擦能量损失越大，并且增加轮胎的接地面积，一定程度上有利于降低轮胎的磨损。此外，由表3可知，对于11.00R20轮胎，酒井秀男理论、Frank理论和新非平衡轮廓理论设计的轮胎的摩擦能量损失分别比现行设计的轮胎增加了2.95%，减小了0.8%和减小了4.34%；而对于385/65R22.5轮胎，酒井秀男、Frank和新非平衡轮廓轮胎的摩擦能量损失分别比现行设计轮胎增加了35.9%，减小了3.03%和减小了24.9%。

2.3 滚动阻力有限元分析

2.3.1 轮胎滚动阻力数值计算

轮胎总的滞后能量损失

ELOSS=∑QiVi

式中：Vi为轮胎橡胶体积；Qi为轮胎单位体积橡胶的迟滞损失量。

通常将轮胎截面单元的应力应变状态沿轮胎一周方向的分布作为该单元一个滚动周期的应力应变循环。利用有限元受力分析获得轮胎的应力应变场，提取出轮胎截面各点材料的应力应变沿轮胎一周的分布，将其视为轮胎在滚动状态下该处的加卸载循环。将应力、应变循环通过傅立叶分解成谐波的叠加，获得不同频率下的应力应变幅值：

(8)

则单位体积轮胎材料在每一个周期中的能量损失为

根据式(8)可求得轮胎滚动阻力Ff：

文献[21]中验证了该计算方法的准确性。

2.3.2 有限元分析结果

本文中模拟轮胎稳态自由滚动状态下的滚动阻力，轮胎气压与负荷按照表2设置，路面附着系数定义为0.7，速度为80km/h。2种规格4种不同轮廓设计的轮胎在稳态自由滚动状态下的滚动阻力如表4所示。

由表4可知，对不同规格的轮胎，3种非平衡轮廓设计的轮胎的滚动阻力呈现了相同的变化趋势，Frank非平衡轮廓轮胎的滚动阻力最大，新非平衡轮廓轮胎的滚动阻力最小。与酒井秀男和Frank非平衡轮廓轮胎相比，新非自然平衡轮廓设计的11.00R20轮胎，其滚动阻力分别降低了12.9%和17.56%；新非自然平衡轮廓设计的385/65R22.5轮胎，其滚动阻力分别降低了3.49%和15.74%。这是由于新非自然平衡轮廓与酒井秀男和Frank设计方案相比具有更平坦的胎面轮廓，可以降低胎肩处胎面胶和垫胶的厚度和应变能，当轮胎受载时，平直的胎侧设计可以将轮胎的变形转移到胎侧，且该设计使轮胎接地压力分布更均匀，有效降低了轮胎的应力应变，最终降低了轮胎的滚动阻力。由此可以看出，轮胎内轮廓对轮胎滚动阻力具有显著影响，新非自然平衡轮廓设计为低滚动阻力轮胎设计提供了指导方向。此外，由表4还可看出，对11.00R20轮胎而言，酒井秀男、Frank和新非平衡轮廓轮胎的滚动阻力分别比现行设计轮胎增加了5.5%，11.5%和降低了8.1%；对385/65R22.5轮胎而言，酒井秀男、Frank和新非平衡轮廓轮胎的滚动阻力分别比现行设计轮胎降低了5%、增加了8.8%和降低了8.3%。对比分析不同轮廓设计轮胎的摩擦能量损失和滚动阻力的变化趋势可知，3种非平衡轮廓设计均可改变轮胎的磨损和滚动阻力，但酒井秀男和Frank的非平衡轮廓设计在改变轮胎磨损和滚阻性能中表现出二者性能间的矛盾，即提升轮胎磨损和滚阻中的某一性能将会降低另一性能，而新非自然平衡轮廓可同时提升轮胎磨损和滚阻性能，即可化解轮胎不同性能之间的矛盾。

表4 轮胎自由滚动下的滚动阻力

2.4 抓地性能的有限元模拟

2.4.1 抓地性能计算方法

在ABAQUS软件中，采用库伦摩擦模型模拟轮胎与路面间的接触[22]：

τcrit=μ×p

式中：τcrit为临界切应力；p为法向接触压强。

当切向力达到临界切应力后，摩擦面之间开始发生相对滑动。模拟轮胎全制动的过程中，当给定摩擦因数时，根据摩擦模型计算出每一时间步对应的切向摩擦应力的合力，通过此切向摩擦力可以评价轮胎的抓地性能[23]。

2.4.2 计算结果分析

轮胎与路面之间的摩擦因数定义为0.7，轮胎气压与负荷按照表2设置。定义路面为刚体，同时给路面施加位移约束。即给路面(沿轮胎滚动方向)足够大的位移实现轮胎与路面间发生相对运动来模拟轮胎的全制动工况。轮胎在全制动滑移过程中的最大切向力如表5所示。

由表5可以看出，2种规格4种不同轮廓设计的轮胎在抱死拖滑过程中的切向力没有明显差异，表明胎体轮廓设计对轮胎抓地性能影响不大。但在3种非平衡轮廓设计轮胎中，酒井秀男轮廓设计的轮胎抱死拖滑时的切向力最大，Frank轮廓设计的轮胎最小。对制动时切向力而言，新非平衡轮廓设计的轮胎抱死拖滑时产生的切向力虽略小于酒井秀男设计轮胎，但差别不大，相对于现行设计轮胎的切向力均有所提升。轮胎与路面间的切向力随着轮胎制动方向位移的变化曲线如图7所示。可以看出，随着路面的移动，切向力均呈线性增加，并在位移达到40mm附近时达到峰值。当切向力达到最大值后，轮胎发生完全滑移，随之切向力稍有降低，此后基本保持不变。

表5 轮胎制动过程中最大切向力

3 结论

(1) 从3种理论设计的轮胎性能有限元模拟结果可以看出，酒井秀男设计理论有利于提升轮胎的抓地性能；Frank设计理论有利于提升轮胎的磨损性能；融合修正后的新非自然平衡轮廓理论有利于提升轮胎的整体性能。本文中认为酒井秀男设计理论更适用于扁平比较大的轮胎，新设计理论更适用于扁平比较小的轮胎，Frank设计理论适用于半钢子午线轮胎。

(2) 传统的设计理论各有优缺点，融合修正后的新非自然平衡轮廓设计为低滚阻轮胎设计提供了方向。新非自然平衡轮廓理论设计的轮胎与现行设计轮胎相比，在减小磨损和降低滚动阻力的同时提高了轮胎的抓地力，提升了轮胎的整体性能，突破了轮胎性能间不相容的难题。

[1] Regulation(EC) of European Parliament and of the Council. No.1222/2009, On the Labeling of Tyres with Respect to Fuel Efficiency and Other Essential Parameters[S]. Official Journal of the European Union,2009.

[2] 2012年中国轮胎出口或遇变数趋势探讨[R/OL].http:// www.chinairn.com/news/20121023/377466.html2012-10-23.

[3] Flanigan C, Beyer L, Klekamp D, et al. Comparative Study of Silica, Carbon Black and Novel Fillers in Tread Compounds[J]. Rubber World,2012,245(5):18-31.

[4] Ko J Y, Prakashan K, Kim J K. New Silane Coupling Agents for Silica Tire Tread Compounds[J]. Journal of Elastomers and Plastics,2012,44(6):549-562.

[5] 马建华,吴友平.炭黑与白炭黑补强溶聚丁苯橡胶和乳聚丁苯橡胶胎面胶性能的对比研究[J].橡胶工业,2012,59(2):84-90.

[6] Jin Chang, Hou Chenyuan, Jin Xiaoxiong. F E Simulation of Tire Wear with Complicated Tread Pattern[J]. Procedia Engineering,2011,15:5015-5019.

[7] Cho J R, Choi J H, Kim Y S. Abrasive Wear Amount Estimate for 3D Patterned Tire Utilizing Frictional Dynamic Rolling Analysis[J]. Tribology International,2011,44(7-8):850-858.

[8] Clark R. Rolling Resistance Basic Foundation[R]. Michelin,2011.

[9] Cho J R, Lee H W, Jeong W B. Numerical Estimation of Rolling Resistance and Temperature Distribution 3D Periodic Patterned Tire[J]. International Journal of Solids and Structures,2013,50(1):86-96.

[10] Liang Chen, Wang Guolin. Study on Tyre-ground Mechanical Characters of TBR Tyres[C]. International Conference on Electric Information and Control Engineering (ICEICE),2011:5411-5414.

[11] 王晨,王国林,张建,等.子午线轮胎性能的多目标优化研究[J].武汉理工大学学报,2010,32(10):69-73.

[12] 潘涛.子午线轮胎轮廓设计理论的相关研究[D].广州:华南理工大学,2011.

[13] 薛梓晨,贺建芸,杨卫民,等.三角平衡轮廓轮胎力学性能的研究[J].北京化工大学学报(自然科学版),2013,40(5):93-99.

[14] Gent A N, Walter J D, Monclal K S. The Pneumatic Tire[M]. Washington D C: U.S.Department of Transportation，National Highway Traffic Safety Administration, DOT HS 810 561,2006.

[15] 刘勇,杨卫民.轮胎结构设计理论研究进展[J].弹性体,2001,11(1):45-49.

[16] 酒井秀男.タイヤ工学[M].東京:株式会社ゲランプリ出版,1987.

[17] 俞淇,丁剑平,张安强,等.子午线轮胎结构设计与制造技术[M].北京:化学工业出版社,2006.

[18] 王国林,万治君,梁晨,等.基于非平衡轮廓理论的子午线轮胎结构设计[J].机械工程学报,2012,48(24):112-118.

[19] 方庆红,路金林,赵立群,等.轮胎磨损分析中接地能量损失的有限元计算模型研究[J].沈阳化工学院学报,2002,16(3):228-231.

[20] 何涛.子午线轮胎胎面磨损有限元分析[D].合肥:中国科学技术大学,2009.

[21] 伍建军.载重子午线轮胎滚动阻力有限元仿真分析[D].镇江:江苏大学,2011.

[22] ABAQUS Inc. ABAQUS Example Problems Manual[R]. ABAQUS Inc.2007.

[23] 梁晨.子午线轮胎综合接地性能评价体系研究[D].镇江:江苏大学,2013.

A Study on the New Non-natural Equilibrium Contour Design ofVehicle Tires with Conflicting Performance Compatibility

Yang Jian, Wang Guolin & Wan Zhijun

SchoolofAutomotiveandTrafficEngineering,AeolusandJiangsuUniversityCooperationInstituteofVehicle,Zhenjiang212013

Based on Sakai Hideo’s and Frank’s non-natural equilibrium contour design theories, a set of integral equations for new non-natural equilibrium contour of inflated tire are proposed. The tire carcasses of two kinds of radial tires for trucks, 11.00R20 and 385/65R22.5 are designed with three different theories of tire contour design. Their performances are then comparatively analyzed with ABAQUS from the aspects of tire wear, rolling resistance and ground grip capability, and also compared with the performance of tire by current design. The results show that Frank’s non-natural equilibrium contour design theory is good at enhancing tire wear performance, Sakai’s non-natural equilibrium contour design theory is conducive to reducing the rolling resistance and improving the ground grip capability of tire, while the new non-natural equilibrium contour design theory proposed can enhance the overall performance of tire and resolve the contradiction between different performances of tire. Compared with tire of current design, the tire designed with new non-natural equilibrium contour design theory can have higher ground grip capability with lower rolling resistance and less wear.

tire; contour design; non-natural equilibrium contour design theory; conflicting performances

*江苏省“六大人才高峰”项目(2011A031)、高等学校博士学科点基金项目(20070299006)、江苏省汽车工程重点实验室开放基金项目(QC201303)和江苏省普通高校研究生科研创新计划项目(CXLX13_676)资助。

原稿收到日期为2014年4月10日，修改稿收到日期为2014年7月1日。