长江南京以下12.5 m深水航道的船舶通航安全风险研究

葛 兵，李亚军

（1.苏交科集团股份有限公司，江苏 南京 210017；2. 江苏省交通运输安全与应急科技研究中心，江苏 南京 210017）

1 概述

长江南京以下12.5 m深水航道建设工程是在长江口深水航道的基础上，将12.5 m水深从太仓上延至南京，全长约280 km。工程建成后将实现长江口航道与南京以下深水航道无缝对接，五万t级海轮可直达南京，兼顾10万t级散货船及以上海轮减载乘潮通航的要求。随着一期工程太仓至南通段的顺利完工，20万t级的好望角型巨轮“首荣和谐”号通过减载顺利抵通，船舶的大型化对航道水深有更高要求，加上该航段繁忙的船舶交通流，深吃水船舶的通航面临着搁浅和碰撞的安全风险。

关于船舶通航安全，有从人、船、环境所组成系统的角度出发，对船舶交通危险程度进行探讨研究[1]；也有从避碰的角度出发，在综合考虑船舶交通数据和船舶动力学的基础上，构建了船舶碰撞几何概率模型[2]；而针对长江深水航道的船舶通航安全，也有不少学者从深吃水船舶通航的可行性、深水航路调整的必要性、深水航道乘潮水位的利用分析以及通州沙标段水上通航安全分析等方面开展了相关研究[3-6]。

本文主要研究长江航道深吃水船舶的通航安全风险，由于深吃水船舶的安全航行主要受限于水深，加上内河避碰规则和长江江苏段的船舶定线制也已对船舶航行与避碰作出了相关规定，而且超大型船舶进出长江一般采取拖轮护航和一定的交通管制，因此这里暂不考虑船舶的碰撞风险，主要对深吃水船舶的搁浅风险开展研究。深吃水船舶在航道中航行时受下坐、横倾和纵倾引起船舶吃水变化的影响，其中船舶的横倾和纵倾主要是受波浪和风影响而引起的吃水变化，而船舶下坐主要是指由于浅水效应而引发的船舶尾部下沉。作者基于船舶下坐、横倾、纵倾和波浪的影响构建了深吃水船舶搁浅模型，选用5万t级油轮、5万t级集装箱船、10万t级散货船和20万t级散货船作为代表船型，采用蒙特卡洛概率仿真法探讨不同船型在不同航速下的船舶搁浅风险。

2 船舶搁浅的数学模型

船舶航行于航道中，当船底与航道底部相接触时，即当龙骨下总体水深（UKC）为零时，船舶就会发生搁浅。深吃水船舶航行时，由于船底距离航道底部较近，船体周围的压力场导致水-淤泥接触面的不规则波动，这些波动会增加船舶沿船长方向的垂向力，垂向力的增加可能引发船舶的下沉和纵倾。波浪和横倾同样影响船舶的吃水变化，致使船舶产生搁浅。由于长江航道中风浪相对较小，船舶航行受波浪影响弱，因此这里主要考虑由于船舶下坐、横倾和潮汐对吃水的影响。

船舶搁浅的数学模型可以用公式（1）表示：

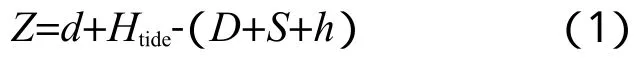
式中：d为航道深度；Htide为潮高；D为设计船型吃水；S为船舶的下坐；h为横倾引起的吃水变化。

2.1 船舶下坐

船体在浅水中航行下坐，主要包括船体整体下沉和纵倾变化两部分。1967年Tuck利用细长体理论首先给出了一种估算方法。之后，在此基础上，出现了许多解析式或半经验的计算公式[7]，如Hooft公式（1974）、Huuska公式（1976）、Eryuzlu公式（1978）、Barrass公式（1981）、Romisch公式（1989）、Millward公式（1990）、Millward公式（1992）、Eryuzlu公式（1994）、Ankudinov公式（1996）。但这些经验或半经验的公式在船舶下坐计算中并没有考虑航道底部浮泥的影响。在参考文献[8]中Delefortrie and Vantorre研究了水-泥接触面的波动情况以及它与船舶下坐的关系，并且提出了浮泥水域航行时船舶下坐的数学模型。该模型可由公式（2）表示，船舶下坐的计算公式由公式（3）～（5）推导得到，其能够有效地预测船舶航行于航道中的下坐量。

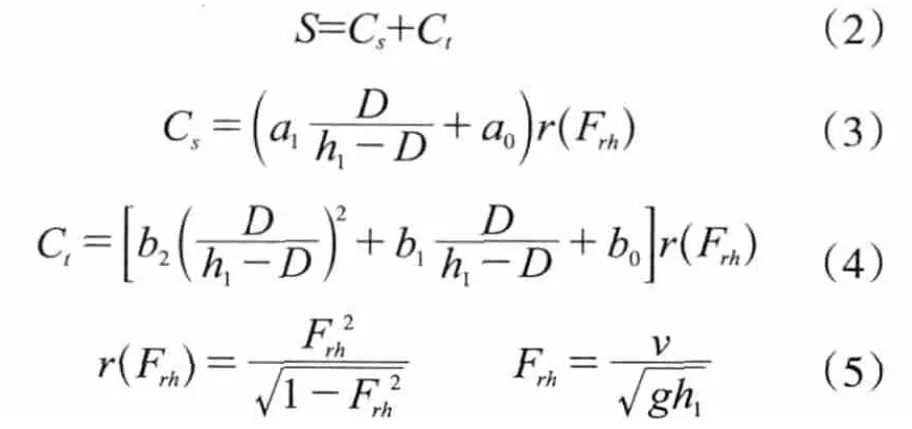
式中：Cs为船舶下沉量；Ct为船舶纵倾；h1为浮泥层以上的水深；D为设计船型吃水；Frh为与深度相关的froude数；v为船速；g为重力加速度；ai、bi为回归系数（i=0，1，2）。

2.2 船舶横倾引起的吃水变化

横倾是指船舶自正浮状态向左舷或右舷方向倾斜的一种浮态，由于长江中航行的船舶受波浪影响较弱，此处仅考虑由于船舶转向操作引起的横倾，波浪引起的横倾暂不计算。船舶横倾导致吃水变化如图 1 所示（图中：C为船舶重心；α为横倾角；h为吃水变化）。由此可以推出h的计算公式：

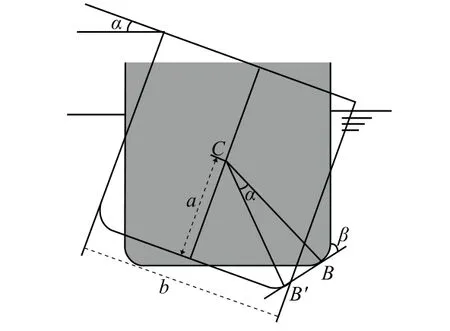
图1 船舶横倾引起的吃水变化示意图

3 蒙特卡洛仿真

蒙特卡洛方法，又称计算机随机模拟方法，是一种基于“随机数”的计算方法。该方法的基本思想就是用事件发生的“频率”来决定事件的“概率”。船舶在航道中运动，引起吃水变化是高度复杂的过程，涉及了多种因素，从船舶搁浅概率的数学模型中可以发现许多因子是随机的，而且符合某种统计分布特征。因此可以根据蒙特卡洛方法求取船舶搁浅概率，即P（Z<0），通过研究上式中各因素的概率密度函数，产生大量的随机数序列，最后统计船舶搁浅的频率以代替搁浅概率。

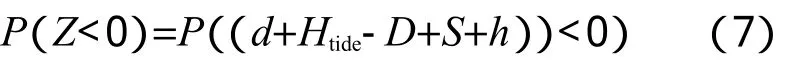
船舶搁浅概率的数学表达式可以由公式（7）表示，即需要对公式中各个参数的概率密度函数进行研究，其中航道深度d和设计船型吃水D为定值常数，则只需要对船舶的下坐S、横倾引起的吃水变化h和潮高Htide的概率密度函数进行研究，然后通过蒙特卡洛产生的随机数模拟出船舶的搁浅概率。

船舶在航道中航行时，由于航道底部浮泥的密度相对水较大，黏性也比较大，会产生比较大的吸力，致使船舶的下坐量增加。特别是深吃水船舶高速航行时，使得浮泥具有相对较大的流速，浮泥的黏性增加，施加于船体的吸引力增大，致使船舶搁浅的概率增加。浮泥对船舶运动的影响主要与船速有关，船速越大船舶搁浅概率越大。且深吃水船舶在淤泥水域航行时存在极限航速，即速度达到极值时再增加就会导致船舶下沉量变大而导致搁浅。为了探明不同船速时船舶下坐对船舶搁浅概率的影响，选取极限船速、中间速度、维持操纵能力的最小船速3个等级的船速做蒙特卡洛仿真实验。

4 实例分析

本文选取长江南京以下12.5 m深水航道二期工程中的福姜沙水道为研究对象，探讨不同船型在此水道航行时的搁浅风险。福姜沙是二期工程中极具代表性的浅险区，其位于江阴以下长江口潮流界变动区，下游紧挨有双湖沙、民主沙、长沙等沙洲，进口鹅鼻嘴处江面宽1.4 km，河床窄深，至长山江面放宽至4.1 km，其后福姜沙分左右两汊，右汊为鹅头型弯道，即福南水道，分流比为20%；左汊顺直，为主汊，分流比约80%，左汊下段又分为福北水道和福中水道。其中福南水道维护水深为理论基准面下10.5 m，是深吃水大型海轮的主航道。这里拟选择福南水道作为深水航道主航路，以假设其维护水深达到12.5 m来对不同船型的船舶搁浅风险进行论证。

4.1 设计船型

长江南京以下12.5 m深水航道二期工程建设完成后，可满足5万t级集装箱船（实载吃水≤11.5 m）和5万t级其他海轮减载双向通航，兼顾10万t级散货船减载通航，其中江阴长江大桥以下兼顾10万t级以上散货船减载通航。为了探讨不同船型在福姜沙水道的搁浅风险，本文选择5万t级的油轮和集装箱船、10万t级的散货以及20万t级的散货作为代表船型，具体船舶参数如表1所示。

4.2 数据处理

对于公式（7）中的航道水深，由于本文是对二期工程建设完成后的福姜沙水道的船舶搁浅风险进行论证，此处取d=12.5 m；设计船型的吃水按照深水航道规定的最大实载吃水取D=11.5 m。

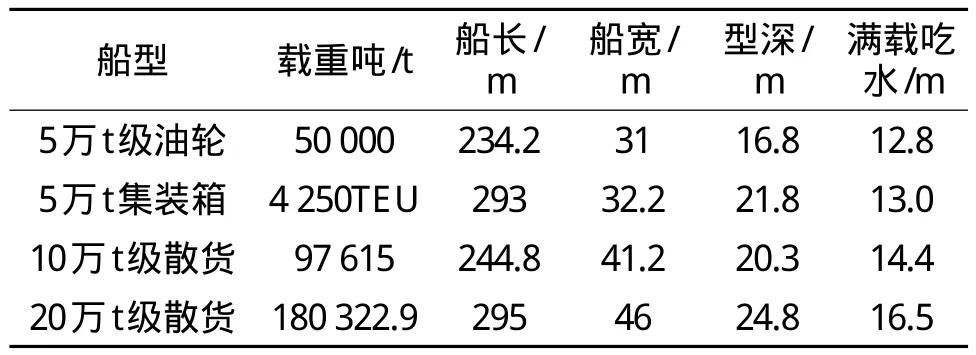
表1 设计船型船舶参数

关于潮高，福姜沙水道受潮水影响明显，一天涨落2次，潮时比江阴略早（10～30 min），为不规则半日潮；大潮（潮差1.80 m以上）时，低潮后1.5 h开始平流，转涨流至高潮后1.5 h；小潮（潮差1 m以下）高潮前2 h水流转缓。福姜沙水道多年平均高潮位为黄海基面2.13 m，相对于当地理论深度基准面2.87 m，故取Htide=2.87 m。

关于横倾引起的船舶吃水变化，此处只考虑船舶转向操作引起的横倾，该值大小与船型、船速、所操舵角、重心高度、初稳心高度等因素密切相关，实际研究表明因操舵引起的横倾值一般不超过5°[9]，因此本文选取±3°横倾角范围内的泊松分布作简化处理。

对于船舶下坐引起的吃水变化，这里以不同的船速来研究其变化。《长江江苏段船舶定线制规定（2013）》中规定船舶正常航行时最高航速不得超过15 kn，最低航速不得低于4 kn，船舶在泰州长江公路大桥桥区水域下界浮以下通航分道内正常航行时最低航速不得低于6 kn。因此，本文选取15 kn和6 kn节作为船速的上下界限，以[10，15]和[6，10]两区间内船速的正态分布特征来研究船舶下坐量的变化规律。

4.3 船舶搁浅风险仿真

基于上一步骤数据处理得到的搁浅模型相关数据，采用蒙特卡洛仿真法对不同代表船型在福姜沙水道的搁浅风险进行仿真，仿真结果如图2所示。

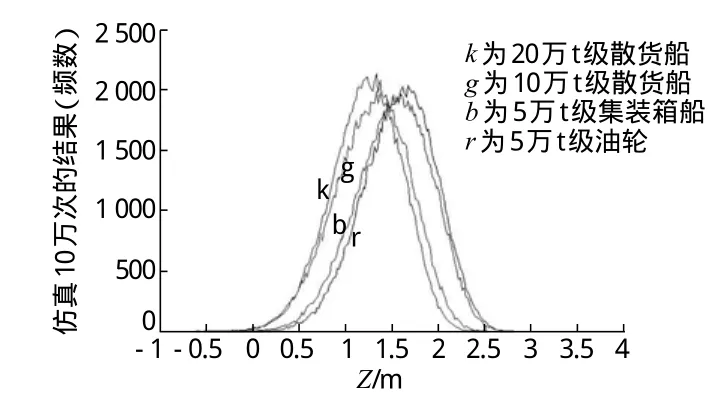
图2 船速分布在[10，15]之间的仿真结果

从图2可以看出，10万t级、20万t级散货船的仿真曲线相比5万t级的油轮和集装箱分布相对靠左，10万次仿真结果中分布在0以下的次数相对较多，搁浅风险相对较大，4种代表船型的具体搁浅数据如表2所示。

在10万次的仿真结果中，不同船型的搁浅次数随船舶吨位的增加有增大的趋势，其中10万t级散货船的搁浅风险最大。如果在深水航道航行保留1 m的富余水深，4种代表船型的搁浅风险都相对较高，只有5万t级油轮保证安全航行的概率在90%以上，而10万t级和20万t级的散货还不到80%。较高的船舶搁浅风险可能与船舶速度相关，因为在[10，15]的速度分布区间，可能船速在12 kn以上及在极限航速15 kn时船舶搁浅风险增加。为此，再以[6，10]的速度区间进行仿真，结果如图3所示。

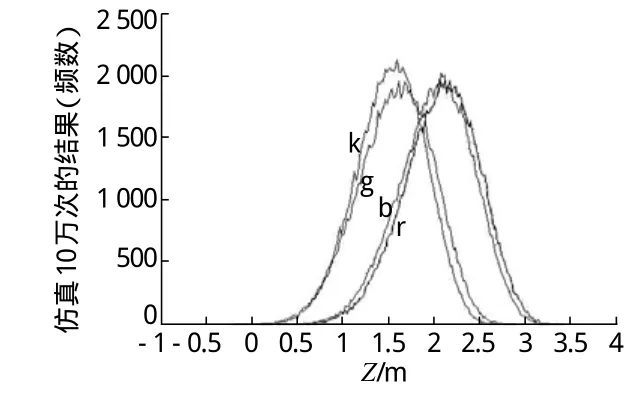
图3 船速分布在[6，10]之间的仿真结果

对比图2和图3的仿真结果可以发现，5万t级的油轮和集装箱船的分布曲线在[6，10]的速度区间时明显右移，而10万t级与20万t级的散货船变化不大，说明船速对5万t级的油轮和集装箱船的搁浅风险影响较大，而对于10万t级及以上的超大型货轮影响相对较弱，相反浅水效应对超大型船舶的影响则更为剧烈。

5 结论

足量的水深是保证深吃水船舶通航安全的首要条件，本文基于复杂的船舶搁浅机制建立了船舶搁浅模型来探讨深吃水船舶的搁浅风险，并利用深水航道二期工程福姜沙河段的现有水文信息和拟建成的12.5 m水深数据，通过蒙特卡洛仿真法对船舶的搁浅风险进行了仿真。结果表明，对于5万t级的油轮和集装箱船可以通过航速的限制来有效控制船舶搁浅风险；而对于10万t级及以上的超大型巨轮限于其尺寸，受浅水效应影响更为剧烈，可以通过拖轮护航和减载等方法确保其安全通航。

[1]吴兆麟.海上避碰与交通安全研究[M].大连：大连海事大学出版社，2001：465-469，507-510.

[2]Montewka，J.，Hinz，T.，Kujala，P.，et al. Probability modelling of vessel collisions[J]. Reliability Engineering & System Safety，2010，95（5）：573-589.

[3]辅金亚，张庆九，卢萍，等.11.5 m吃水海船进出南京及以下港口可行性研究[J]. 中国水运（上半月），2012，（10）22-24.

[4]王炜, 唐仁康. 长江江苏段深水航路调整的必要性和可行性[J].中国水运，2014（3）：53-55.

[5]佘俊华.长江南京以下12.5 m深水航道一期工程乘潮水位利用分析[J].水运工程，2013（2）：1-4.

[6]孙洪河.长江南京以下深水航道工程通洲沙二标段水上通航安全分析[J].中国水运，2013，13（12）：67-68，21.

[7]洪碧光，于洋.船舶在浅水中航行下沉量的计算方法[J].大连海事大学学报，2003，29（2）：1-5.

[8]G. Delefortrie，M. Vantorre，K. Eloot and et al. Squat prediction in muddy navigation areas[J]. Ocean Engineering，2010，37（16）： 1464-1476.

[9]Schoenmakers N.W.A.，WIT A.B.F de. Probabilistic Design Entrance Channel Port of Cape Town[J]. Minor thesis Hydraulic Engineering，2006.