行波激励下不对称连续刚构桥的动力响应

陈 涛，马新勇，胡艳丽

（1.中交一公院 中交瑞通路桥养护科技有限公司，陕西 西安 710075；2.贵州省建筑设计研究院，贵州 贵阳 550000）

1 概述

地震地面运动是复杂的时间-空间运动变化过程，在时间和空间上均具有极高的变化性。在一次地震中桥梁跨度范围内不同桥墩处场地的地震运动过程是不同的，在以往的计算中，常采用简化的方法，只考虑地震波的时间变化性，而不考虑波的空间变化性。严格来说任何结构的地震反应分析都需要考虑地震动时间、空间的差异性影响。尤其是大跨径刚构桥的主墩可能位于不同类型的场地土上，在地震反应分析中各点支承应采用不同激励，即多点激振的方法[1-3]。即使主墩支承处土类型差别不大，也会因地震波沿桥前进方向先后到达主墩的时间差，导致在主墩处输入地震时程的相位差不同，简称行波效应。有地震现场实测资料显示，即使对于50 m跨度的桥墩基础，桩基测点受振动的幅值和相位差别巨大。因此，高墩大跨度桥梁在地震反应分析中就必须考虑在各主墩处采用不同的激励——多点激励问题[4-5]。

本文通过桥梁主墩多点激励的运动方程，介绍了不等跨桥梁在行波作用下的反应分析方法，利用有限元分析软件对一座3跨不对称T构双肢薄壁高墩连续刚构桥进行了多点激励及一致激励下的行波反应分析，并对两种计算参数下的结果进行对比。

2 建立有限元方程

一致激励地震作用下一般多自由度体系结构的地震动方程为：

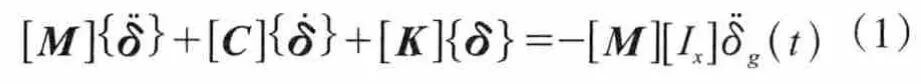
式中：{δ}为位移矢量；[K]、[M]和[C]分别为质点系的刚度矩阵、质量矩阵和阻尼矩阵；为地面加速度时程，等式右端方程为地震地面加速度水平方向引起的激振力[4]。

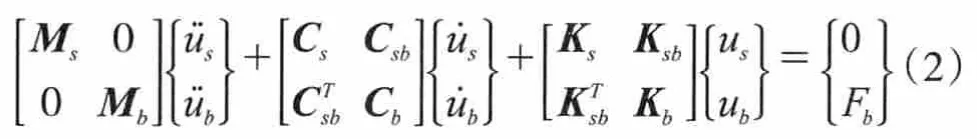
对于高墩大跨径连续刚构桥，在主墩处地震激励不同，各主墩运动方程与一致激励下的地震运动方程不同，可通过分块的形式来表达：式中：Ks、Cs、Ms分别为非支承处的刚度矩阵、阻尼矩阵和质量矩阵；分别代表支承处和非支承处自由度的位移向量、速度和绝对加速度；Kb、Cb、Mb分别为支承处的刚度矩阵、阻尼矩阵和质量矩阵；Fb为地震作用在桥墩支承处产生的反力。

通过模拟静力位移方法求解方程（2）时，将非支承处的Us（绝对位移向量）分解成us（模拟静力位移向量）和vs（动态相对位移向量）二者的和，公式如下：

公式中模拟静力位移us为：

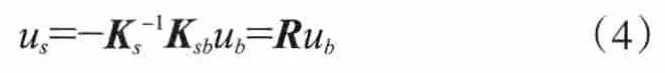
其中，R为影响矩阵。

求解方程，将式（3）、式（4）代入式（2）可以求得：

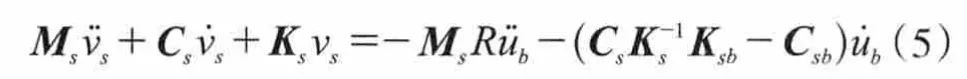
不考虑支承运动速度）作用的阻尼力，令公式中=0，则得到新的简化公式：

此方程即为大跨度桥梁在多点不同步地震激励作用下的运动方程。

考虑行波作用效应，直接赋予式（6）右端的加速度时程不同的加速度。

3 工程实例

某高速公路大桥桥梁全长415 m，为（130+200+85） m预应力混凝土连续刚构，是由1个240 mT和1个160 mT组成的不对称结构。桥面总宽22.5 m，宽度组成为0.5 m（护栏）+10.0 m（行车道）+1.5 m（中间分隔带）+10.0m（行车道）+0.5 m（护栏）。道路等级为山岭重丘4车道高速公路，设计行车速度60 km/h。设计荷载：汽—超20级，挂—120。

以上述运动方程为理论支撑，利用有限元分析软件对大桥建立全桥结构离散模型（如图1所示），模拟实际情况，但不考虑桩基础的作用，视墩底为固结端。单元杆系为空间三维梁单元，主梁为变截面箱梁，桥墩为双肢薄壁墩。模型的边界条件为：（1）基础全部约束；（2）墩顶处主梁和墩柱节点刚性连接；（3）边跨处支座约束有扭转和竖向位移。

图1 结构离散模型

3.1 多点激励地震波分析[6-7]

本文运用时程分析法对大桥进行地震反应分析，根据大桥桥位处场地情况选取EL-Centro波分别从桥梁3个方向（大桥横、纵、竖向）同时输入模型计算，选用竖向加速度峰值为0.025 g，水平方向的加速度峰值为0.05 g，模型计算时取地震运动前40 s，时长0.02 s，共2 000步。在模型分析过程中，分别采用ELCentro波的东西向、南北向和竖向作用输入大桥的横向、纵向和竖向。

对大桥模型分别采用非一致激励和一致激励进行分析。非一致激励分析对大桥（横、纵、竖向）3向同时进行行波输入。根据大桥桥位处场地情况，选取视波速v分别为200 m/s、250 m/s、500 m/s、1 000 m/s、2 000 m/s，根据大桥主跨跨径l=200 m和所选择的视波速v，可由公式△t=l/v，确定大桥桥墩处地震输入的时间差△t分别为0.1 s、0.2 s、0.4 s、0.8 s、1.0 s，输入模型进行分析，得到行波效应的内力响应计算结果，并与模型在一致激励地震运动下的计算结果进行分析对比。

3.2 模型结果对比

根据上述有限元模型及参数，可得到大桥在地震作用下考虑行波效应和一致激励两种情况下关键截面的地震时程反应，计算结果如表1～表6、图2～图6所示。

（1）对大桥计算结果进行分析，得到如下结果：对于轴力，长T轴力大于短T的轴力；对于剪力，短T的纵向剪力远大于长T，而横向剪力相差不大；对于弯矩，纵向弯矩相差不大，长T的横向弯矩较大。这是由于主梁对各墩纵向产生强大的约束，使得桥墩及T构上的地震内力响应按墩的纵向线刚度（EI/l）进行重新分配，1#、2#墩墩高相差不大，从而平均分担了纵向内力；又因为主梁对桥墩面外的约束较小，桥墩上的地震内力响应主要由自身承担，相对于短T，长T因质量大而分担了较大的横向内力。

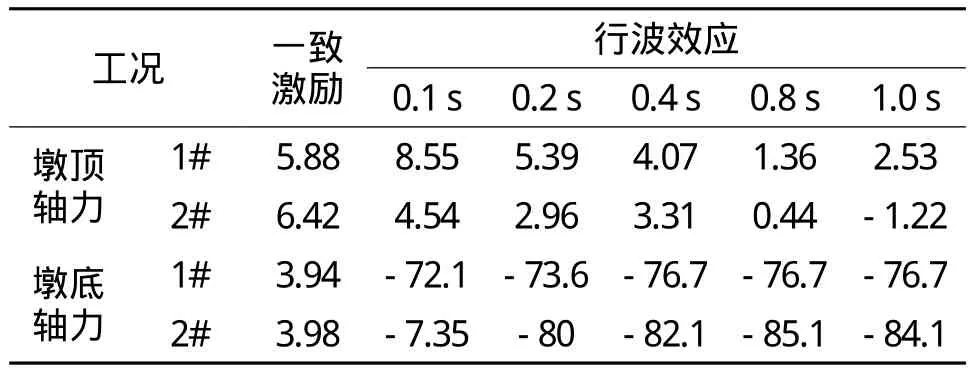
表2 1#、2#墩顶、墩底轴力峰值 103 kN

表3 1#、2#墩顶剪力峰值 103 kN

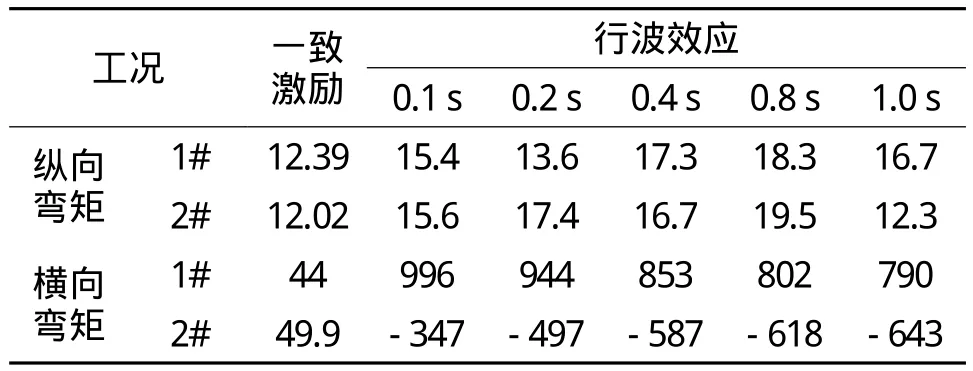
表4 1#、2#墩顶弯矩峰值 103 kN·m

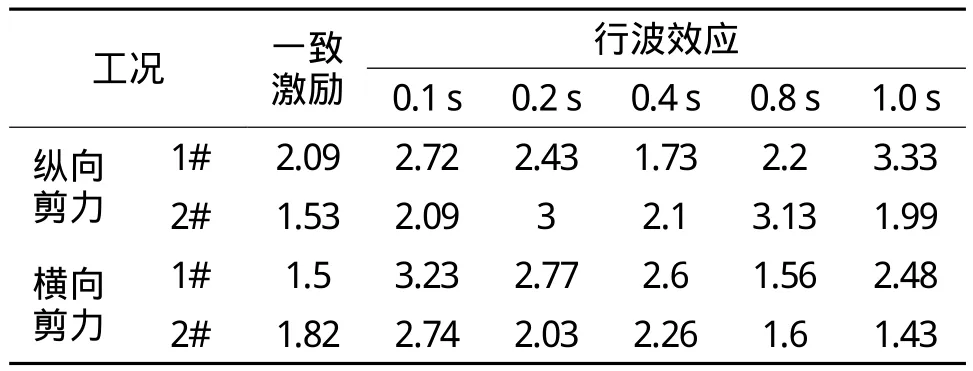
表5 1#、2#墩底剪力峰值 103 kN

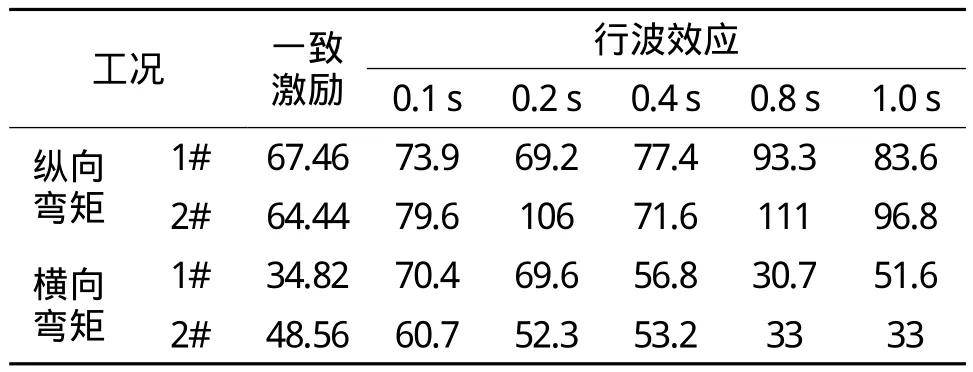
表6 1#、2#墩底弯矩峰值 103 kN·m

（2）从表1计算结果及图2可以得到，考虑行波效应时长、短T桥墩顶纵向位移结果减小，随着时间差△t逐渐减小（即视波速v逐渐增大），墩顶纵桥向水平位移与一致激励时的位移响应相接近，总体上看是在低波速段振荡变化，随后逐渐接近一致激励时的位移响应。由图表可以看出按一致激励计算的水平位移大，墩顶纵桥向水平位移在一致激励时结果是时间差1.0 s时的2倍，结果偏安全。结构的振动周期随时间差的逐渐增大而延长。

图2 2#墩墩顶纵向位移时程对比

图3 1#墩墩顶纵向剪力时程对比

图4 2#墩墩顶纵向弯矩时程对比

图5 2#墩墩底横向剪力时程对比

图6 1#墩墩底纵向弯矩时程对比

（3）从表2计算结果可以得到，考虑行波效应的计算结果，轴力峰值在桥墩墩顶、墩底基本上是减小的，轴力峰值随着时间差的逐渐减小而逐渐增大。

（4）从表3计算结果和图3，可看出行波效应的计算结果，随着时间差的逐渐减小，墩顶纵向剪力峰值总体呈上升趋势，但比一致激励的剪力大；而随着时间差的逐渐减小，墩顶横向剪力 峰值时而增大时而减小，规律性不强，而且峰值在整个过程中的变化幅度较小，行波效应对其影响很小。对比长T（1号墩）和短T（2号墩），行波效应对短T墩顶纵向剪力峰值的影响较大。从表5计算结果和图5看出，行波效应对墩底剪力峰值的影响不大，随着时间差的减小，没有规律性可循，且整个过程中峰值变化幅度较小。

（5）从表4计算结果和图4可以看出，随着时间差的减小，1#、2#墩顶纵向弯矩峰值变化幅度较小，行波效应对纵向弯矩的影响很小。随着时间差的逐渐减小，1#墩墩顶横向弯矩峰值逐渐增大，峰值变化幅度小于28%，从计算结果可看出一致激励时的响应小于行波效应时的响应；随着时间差的逐渐减小，2#墩墩顶横向弯矩峰值逐渐增大，从计算结果可看出一致激励时的响应大于行波效应时的响应。

（6）从表6计算结果和图6可以看出，行波效应对墩底纵向弯矩影响较小，弯矩峰值在考虑行波效应时，峰值都有一定程度的增大。1#、2#墩墩底横向弯矩峰值随着时间差的逐渐减小，峰值时而减小时而增大，没有规律性可循。

4 结论

本文通过运用大跨径连续刚构桥在行波作用下的地震反应分析方法，建立了一座3跨预应力混凝土连续刚构桥在行波激励下地震反应的建模计算，通过与一致激励地震作用下的计算结果进行对比,得到以下结论:

（1）短T的位移较小，长T的位移较大，承担的力较大；由于桥墩在纵向、横向受到主梁的约束，较大的横向内力由质量大的墩承受。

（2）连续刚构桥的振动反应受地震波行波效应的影响显著。计入行波效应影响时，结构内力计算结果有不同程度增大，而结构位移计算结果却出现减小趋势，结构的振动周期延长。所以在对桥梁进行抗震设计时，应当计入行波效应对高墩大跨连续刚构桥的影响，偏安全地考虑地震响应对结构的最不利影响。

（3）结构动力响应计入行波效应的影响,比仅考虑一致激励地震波向前迈进了一步,但地震波波形随机变化以及波的频散性和相干效应无法考虑周全，使得分析结果存在一定程度的局限性。地震过程发生在一瞬间，仿真模型中考虑行波效应、局部场地效应和部分相干效应的影响能够更加准确地反映实际情况，计算结果更为合理,因此按多点激励的地震输入模式建立随机地震动模型,对大跨径桥梁结构进行地震反应仿真分析，今后需进一步提高对这些因素的综合考虑。

[1] 范立础.桥梁抗震[M].上海：同济大学出版社，1996.

[2]郑史雄，奚绍中，杨建中.大跨度刚构桥的地震反应分析[J].西南交通大学学报，1997.32（6）：586-592.

[3]范立础，胡世德，叶爱君. 大跨度桥梁抗震设计[M].北京：人民交通出版社，2001.

[4]李国豪.桥梁结构稳定与振动[M].北京：中国铁道出版社，2002.

[5]李忠献，史志利.行波激励下大跨度连续刚构桥的地震反应分析[J].地震工程与工程振动，2003，23（2）：68-76.

[6]GB 50011—2001建筑抗震设计规范[S].

[7]TG/T B02-01—2008公路桥梁抗震设计细则[S].