基于t分布变异的蝙蝠算法

常 青，贺兴时

（西安工程大学理学院，陕西西安 710048）

基于t分布变异的蝙蝠算法

常 青，贺兴时

（西安工程大学理学院，陕西西安 710048）

为了进一步提高BA算法的性能，提出一种基于t分布变异的蝙蝠算法（TMBA）.该算法通过对最优的蝙蝠个体进行高斯变异，对非最优蝙蝠个体进行自适应t分布变异，使得算法在进化初期具有良好的全局探索性，而在进化后期具有较优的局部开发性.通过选取6个典型函数对BA、ABA和TMBA进行对比实验，结果表明TMBA优于BA、ABA.

蝙蝠算法；t分布变异；高斯变异

0 引 言

蝙蝠算法是基于微蝙蝠回声定位行为提出的一种元启发式算法，并已广泛地应用于复杂优化问题.蝙蝠算法（Bat Algorithm，BA）［1］是2010年由Yang提出的一种基于种群随机寻优的全局优化算法.由于该算法模型简单，收敛速度快，已广泛应用于多目标优化［2］、工程优化［3］等问题中.为了进一步提高算法的性能，国内许多学者对蝙蝠算法进行了改进.文献［4］开发了一种混合蝙蝠乍法，使用差分进化作为蝙蝠算法局部搜索的一部分，改进了该算法.文献［5］将蝙蝠算法与和声搜索结合，产生了用于函数基准数值优化的混合蝙蝠算法.文献［6］将模拟退火的思想引入到蝙蝠优化算法中.这些改进算法在不同程度上提高了算法的性能.但是，针对高维目标函数的改进方法，目前成果较少.

本文针对BA易早熟，对高维函数寻优精度低等缺陷，在分析原有算法优化机理的基础上，提出一种基于自适应t分布变异的蝙蝠算法，在优化过程中，对最优的蝙蝠个体进行高斯变异，对非最优蝙蝠个体进行自适应t分布变异，使算法有效摆脱局部极值的束缚，同时提高了该算法的收敛速度和解的精度.

1 蝙蝠算法和变异策略

1.1 蝙蝠算法

蝙蝠算法是在理想的状态下，利用蝙蝠在觅食时所发出的脉冲的频率、音强、脉冲发射频度的变化而模拟设计出的一种群智能算法.为模拟蝙蝠的回声定位特征，理想化的假设如下［7］：

（a）所有蝙蝠利用回声定位感应距离，并能够判断猎物和障碍物之间的差异.

（b）蝙蝠是以速度Vi、位置Xi和固定频率f（或波长λ）随机飞行的，并用可变化的波长λ（或频率f）和脉冲音强A来搜索猎物，它们会根据猎物的接近程度调整其发出的脉冲频率.

（c）虽然音强在不同形式下变化不同，在这里假设音强从一个很大的（正数）A变化到最小值Amin.

基于以上规则，蝙蝠算法的基本步骤可以概括如下：

Step1：参数初始化，最大迭代次数maxgen，蝙蝠种群规模sizepop，蝙蝠的位置Xi，搜索脉冲频率范围［fmin，fmax］，脉冲音强A，脉冲频度r；

Step2：种群迭代，按式（1）分别对蝙蝠的频率fi，速度vi，位置Xi进行更新；

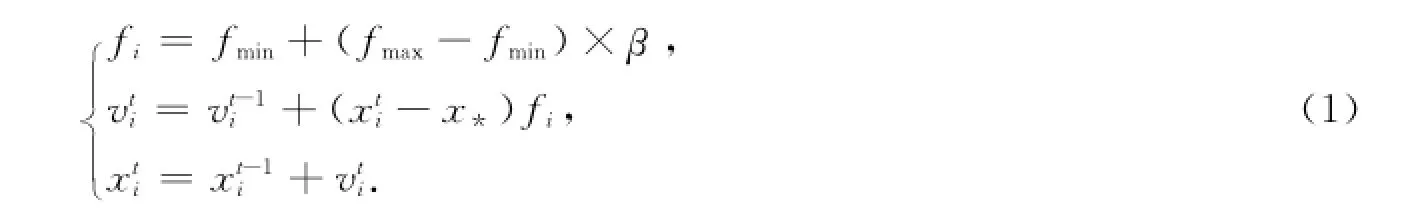
其中，β∈［0，1］是一个服从均匀分布的随机向量.x＊表示当前全局最优解，它是通过比较所有n只蝙蝠搜索到的解而得到的.另外，依据问题需要搜索的范围大小，令fmin＝0，fmax＝O（1）.初始时，每只蝙蝠随机赋给一个频率，这个频率服从［fmin，fmax］间的均匀分布.

Step3：如果rand＞r，选择最优蝙蝠个体，通过随机游走法则在最优蝙蝠个体附近形成局部新解，如式（2）所示，

其中，ε∈［－1，1］是一个随机数，At＝＜Ati＞是所有蝙蝠在同一个时间段的平均音量.

Step4：通过随机飞行产生一个新解；

Step5：如果rand＜A，并且蝙蝠的适应值得到改善，则接收这个新解.按式（3）增大ri减小Ai；

其中，α和γ为常量.

Step6：按照适应值大小蝙蝠群体进行排列，找到当前最优蝙蝠所处空间位置及其适应值.

Step7：迭代寻优，返回Step2，直到满足终止条件为止.

Step8：终止算法，输出最优蝙蝠个体的适应值及位置.

1.2 变异策略

学生t分布又简称为t分布.威廉·戈塞于1908年首先推导发表，t分布含有参数自由度n，而它的曲线形态与n大小有关，自由度n越小，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈高；当自由度n＝1时，t分布曲线为柯西分布曲线.即t（n＝1）＝C（0，1），其中C（0，1）为柯西分布；自由度n愈大，t分布曲线愈接近正态分布曲线，当自由度n→∞时，t分布曲线近似为高斯分布曲线.即t（n→∞）→N（0，1），其中N（0，1）为高斯分布.也就是说标准高斯分布和柯西分布是t分布的两个特例.柯西分布、正态分布、t分布的密度，从图1可以看出，柯西分布尾部曲线呈现长而平坦的形态，正态分布的尾部曲线呈现出短而陡的形态.柯西变异比高斯变异有更大的可能性产生远离亲代的下一代点［8］.

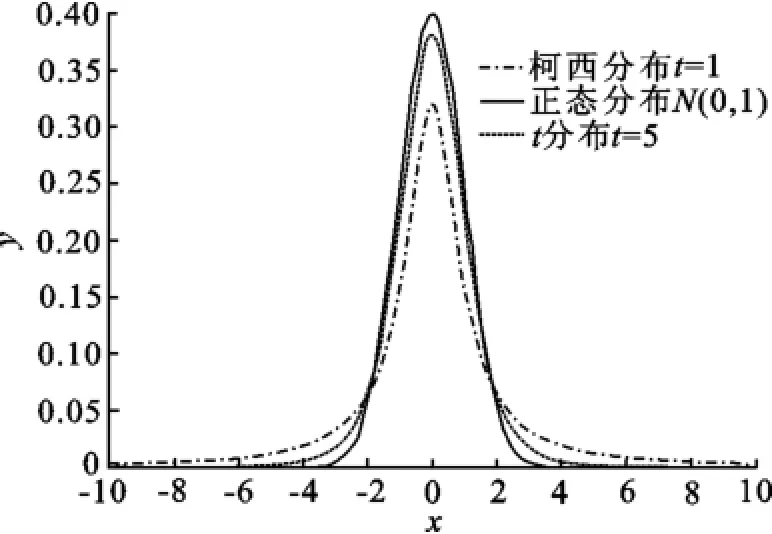
图1 柯西分布、正态分布、t分布的概率密度函数曲线Fig.1 Curves of probability density function for cauchy Gaussian and t distribution

本文对蝙蝠个体X优＝（xi1，xi2，…，xid），采取自适应t分布的变异策略，具体定义如下：X′＝X优＋X优⊗ε.（4）其中，ε和Xi是同阶的随机矩阵，每个元素εi～t（Iteration），⊗表示点乘.式（4）表示在当前蝙蝠个体空间位置Xi的基础上增加了t分布随机干扰项Xi⊗ε，充分利用当前种群的信息进行变异.自适应t分布变异策略使用算法的迭代次数Iteration作为t分布的自由度参数.算法在运行初期Iteration值较小，t分布变异近似于柯西分布变异，具有良好的全局探索性，有助于算法跳出局部最优点，避免过早收敛；算法运行中期，t分布变异介于柯西分布变异和高斯变异之间；算法在运行后期，Iteration值较大，t分布变异近似于高斯分布变异，具有较优的局部开发性，有助于算法提高解的质量，加快收敛速度.因此本文提出的基于自适应t分布变异的蝙蝠算法（TMBA）优势在于，基于t分布的变异策略将高斯分布和柯西分布两者变异的优势结合起来，从而提高了算法的全局探索和局部开发能力，使蝙蝠算法能够跳出局部最优点的束缚，收敛于全局极值点，同时也提高了收敛速度.鉴于高斯分布具有良好的局部开发能力，为提高算法解的质量，还需做的一项工作是，在最优蝙蝠个体上加上一个服从高斯分布的随机扰动项.对最优蝙蝠个体X优＝（x1，x2，…，xd）进行高斯变异定义如下：

其中，Φ和X优是同阶的随机矩阵；每个元素ηi～t（Iteration）；⊗表示点乘.

2 改进的蝙蝠算法

基于自适应t分布变异的蝙蝠算法的思想是为了利用柯西分布的全局探索性和高斯分布的局部开发性，提出一种基于t分布的变异策略［9］.当蝙蝠个体陷入局部最优点时，对当前蝙蝠种群中最优蝙蝠个体采取高斯变异策略，将高斯变异后的蝙蝠个体与全局最优蝙蝠个体的适应值进行比较，取二者最优值替代全局最优值，对其他蝙蝠个体采取t分布变异策略.这样一方面增加了蝙蝠种群的多样性，有利于算法跳出局部最优点；另一方面增强了算法的全局搜索和局部开发的性能，提高了解的质量和算法的收敛速度.在算法迭代过程中，当全局最优值在连续两次迭代过程中没有改变或者变化很小，小于η时，看作蝙蝠算法寻优停滞，启动高斯变异策略和t分布变异策略.算法主要步骤如下：

（a）产生初始化群体.在控制变量可行域内随机生成n个蝙蝠个体，形成初始蝙蝠种群.随机初始化蝙蝠的位置、速度、频率、脉冲频度和脉冲音强.参数beststep表示最优蝙蝠个体连续不变的次数，初始置为0；

（b）评价种群.对当前种群中的每个蝙蝠个体进行评价，找到当前全局最优值.

（c）更新种群.在种群迭代过程中，按式（1）分别对蝙蝠的频率fi，速度vi，空间位置Xi进行更新.

（d）生成随机数rand.如果rand＞r，选择最优蝙蝠个体，通过随机游走法则得到局部新解，如式（2）所示.

（e）评价种群.对当前种群中的每个个体进行评价，若某个个体优于全局最优蝙蝠个体，则全局最优蝙蝠个体更新为该个体.并置beststep为0.

（f）变异条件判断.判断beststep是否已达到预置的连续不变化次数的最大阈值maxstep，或连续两次迭代变化很小（＜η）.若是，执行第（g）步；否则转到第（h）步执行.

（g）变异操作：1.对当前种群中最优蝙蝠个体进行高斯变异，对其他蝙蝠个体进行t分布变异；2.对新形成的蝙蝠种群计算各蝙蝠的函数适应值，并与全局最优值进行比较，如果优于全局最优值，则以自身替换；3.beststep置为0.

（h）终止条件判断：判断是否已达到预置的最大迭代次数Maxgen或判断最优解是否达到了满意的误差界内，若不满足，则beststep加1更新，转到第（c）步执行，进行下一步蝙蝠优化过程；否则转到第（i）步执行.（i）算法终止，输出最优解.TMBA算法流程如图2所示.

3 仿真实验

3.1 基准测试函数

在本次实验中，为了研究TMBA的有效性，选取了6个典型的基准测试函数，其中，Sphere，Zakharov，Sum Squaares为单模态函数，Ackley，Griewangk，Rastrigin为多模态函数，各个函数的搜索空间、全局最优值和函数解析式见表1.

3.2 结果与讨论

为了研究TMBA算法的性能，验证该算法的有效性，本文采用BA、ABA［10］和TMBA 3种算法进行实验对比分析.本文仿真实验均在Matlab 7.11.0（R2010b）环境下运行.具体参数设置为：种群数50，当维数为10，50维时，迭代次数分别为1 000次，2 000次.最小频率值为0，最大频率值设为2，最大脉冲音强A为0.25，脉冲频度r为0.5.

3.2.1 BA，ABA和TMBA寻优结果对比 为了防止算法的偶然性，分别对3种算法独立运行30次，运行结果见表2.其中，平均值反映了算法达到最大迭代次数时解的质量；标准差体现了算法的收敛稳定性.

从表2的结果可以看出，不管对于单模态函数，还是多模态函数，低维函数还是高维函数，基于t分布变异的TMBA算法在解的质量上都明显高于基本BA算法和自适应变异的ABA算法.TMBA算法解的标准差要小于其他两个算法解的标准差，可见TMBA算法更具有稳定性.虽然，各个算法在同一基准函数下，随着维数的增加，解的质量有所下降，但这是合理的，因为解的搜索空间随着问题维数的增加呈指数形式增加.

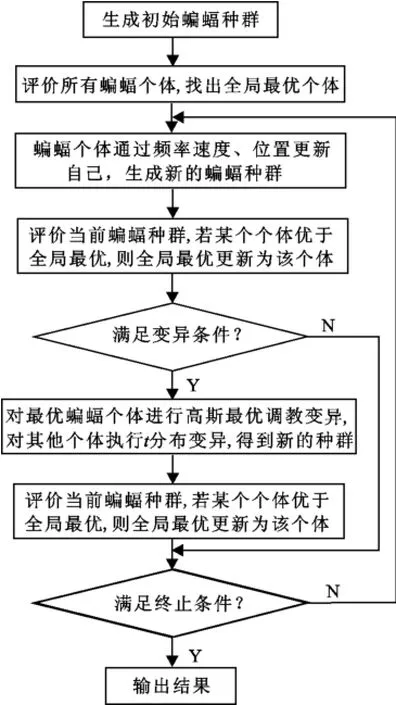
图2 TMBA算法流程图Fig.2 Flow chart of TMBA algorithm

表1 基准测试函数Table 1 Test fnctions

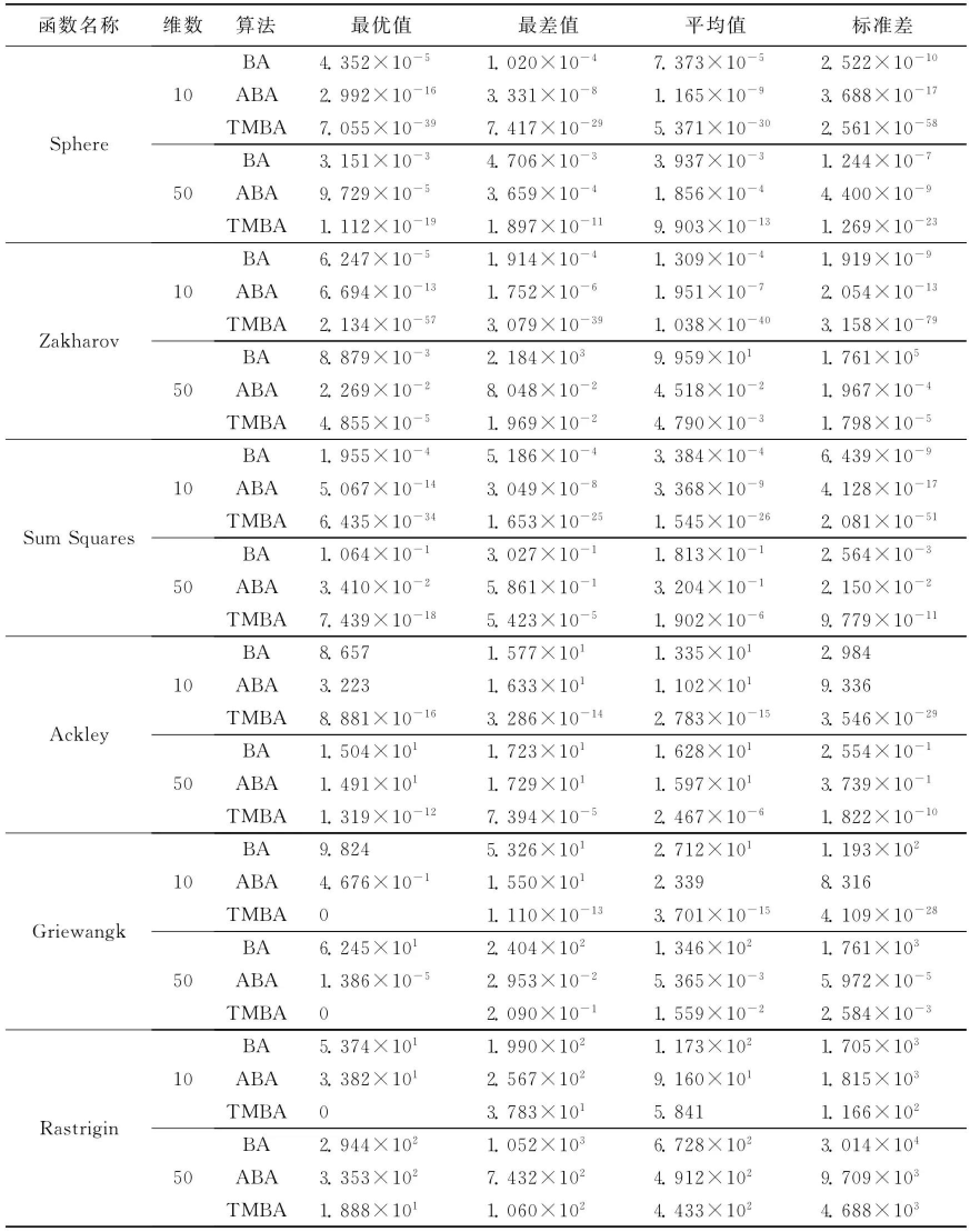
表2 BA、ABA、TMBA对6个基准函数的寻优结果Table 2 The optimization result of BA，ABA，and IBA for six functions

3.2.2 BA、ABA和TMBA进化曲线对比 为了进一步测试TMBA算法的性能，在相同的条件下，对表1所示的基准函数进行仿真模拟，对各算法的进化曲线进行对比，结果如图3～8所示.进化曲线的横轴表示进化的迭代次数，纵轴表示目标函数的适应度值.

Sphere函数是简单的单峰函数，除了唯一的全局最小解，没有局部最小解，是许多单峰函数以及一般优化函数的代表，对于此类函数，大部分算法都能得到一个较好的结果.因此要做的工作是，在高维情况下，改进的算法要尽可能的提高解的精度.函数Sphere进化曲线如图3所示.由图3可以看出，TMBA算法下，测试函数迭代曲线下降速度很快，解的质量明显高于BA和ABA两种算法.解的精度至少提高了20个数量级.Zakharov函数除了唯一的全局最小解，没有局部最小解.函数Zakharov进化曲线如图4所示.从图4可以看出，TMBA的解的质量要高于BA和ABA解的质量.

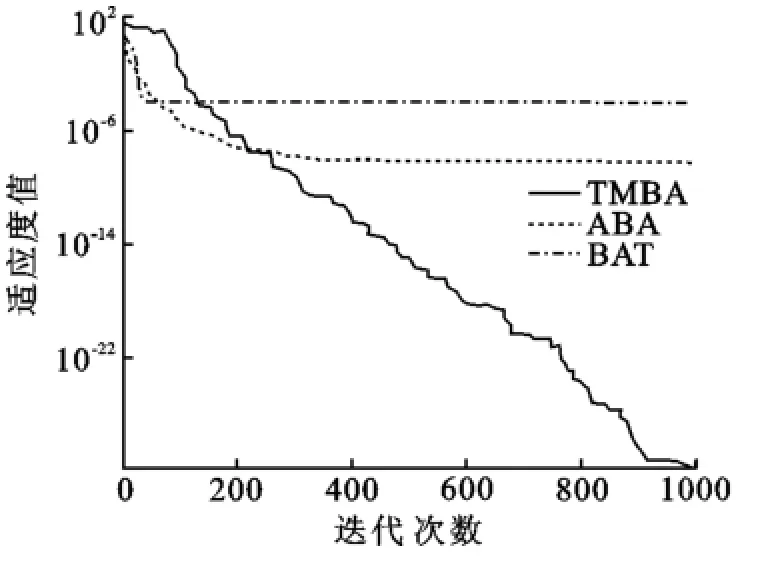
图3 函数Sphere进化曲线Fig.3 Convergence curve of function for Sphere

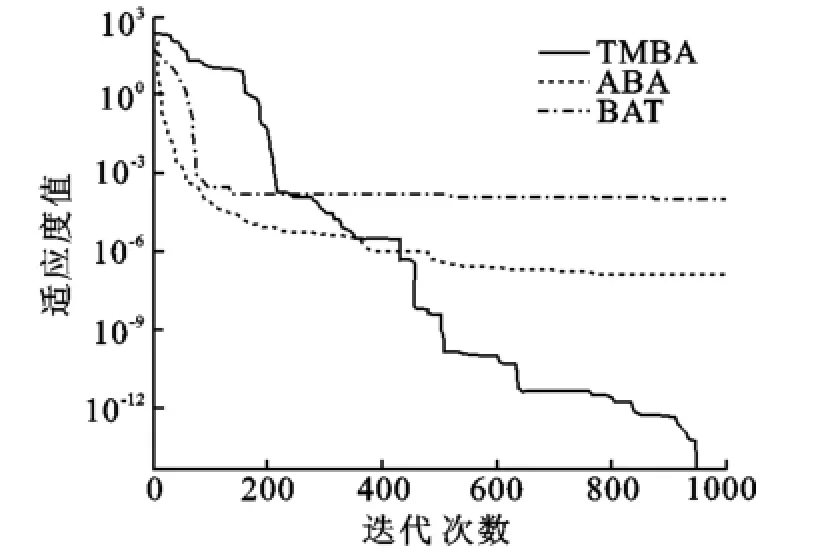
图4 函数Zakharov进化曲线Fig.4 Convergence curve of function for Zakharov

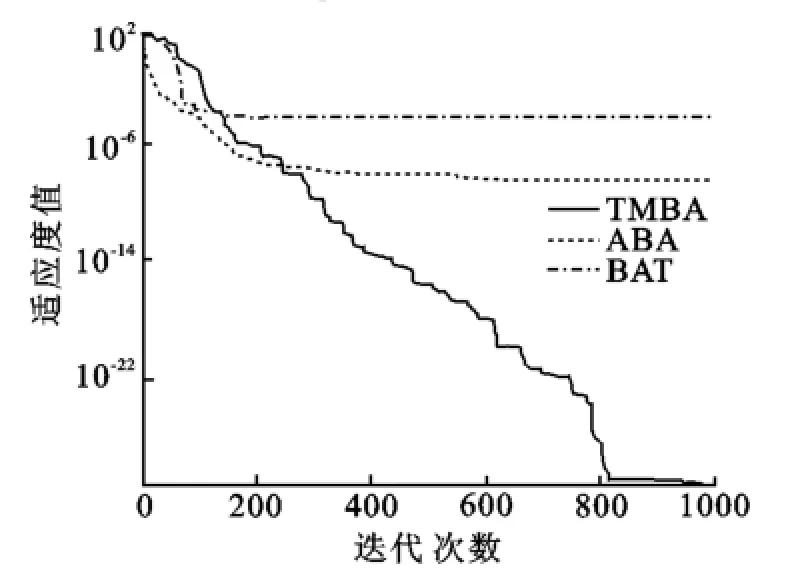
图5 函数Sum squares进化曲线Fig.5 Convergence curve of function for Sum squares

图6 函数Ackley进化曲线Fig.6 Convergerce curve of function for Ackley

对于Sum squares函数来说，BA和ABA的蝙蝠个体容易陷入局部最优点且不易跳出.函数Sum squares进化曲线如图5所示.从图5可以看出，TMBA可以在搜索范围内快速搜索，得到一个精度较高的解.

Ackley函数是多模态函数，有少数的局部最小值，它的特征是几乎平坦的区域由于余弦波的影响而起伏不平.为避免算法陷入局部最优，就要增大问题的搜索区域.基于t分布变异的TMBA算法利用变异增加了种群的多样性，搜索的区域也就更大，在高维的情况下，该函数是测试算法是否收敛的最好工具.函数Ackley进化曲线如图6所示.从图6可以看出，TMBA以较快的速度收敛于一个精度更高的解.解的精度至少提高了10个数量级.

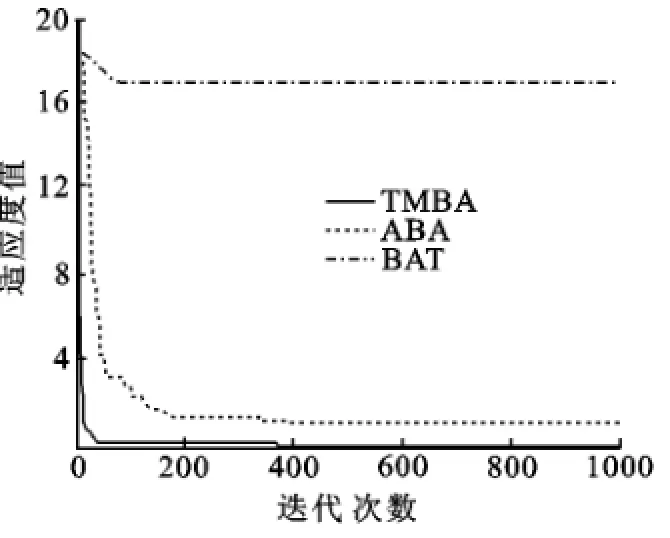
图7 函数Griewangk进化曲线Fig.7 Convergence curve of functionfor Griewangk

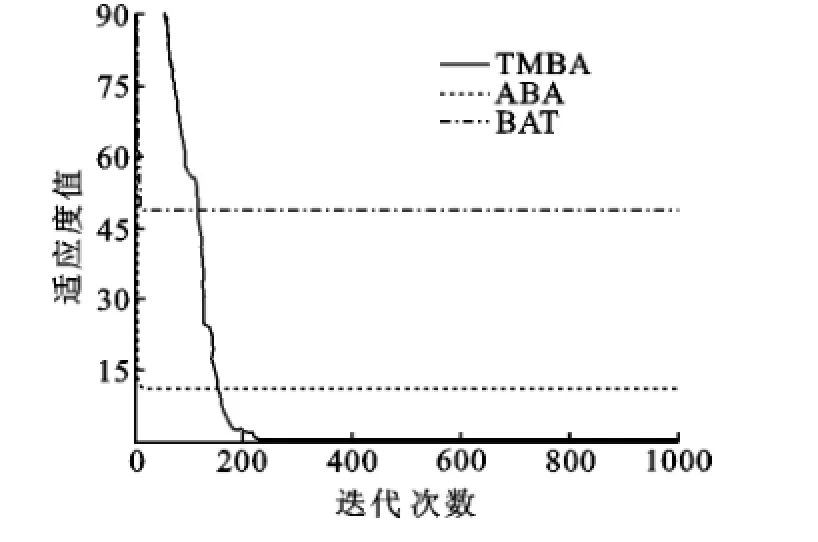
图8 函数Rastrigin进化曲线Fig.8 Convergence curve of functionfor Rastrigin

Griewangk函数是典型的非线性多模态函数，有无数个局部最优解.函数Griewangk进化曲线如图7所示.从图7可以看出，在高维的情况下，TMBA在迭代初期就表现出良好的性能，并以较快的速度收敛于一个精度较高的解.而且TMBA能达到Griewangk函数的理论最优值0.Rastrigin函数是多模态函数，有数个局部最优解.函数Rastrigin进化曲线如图8所示.从图8可以看出，TMBA算法解的精度更高.

4 结束语

蝙蝠算法是一类新型的搜索全局最优解的随机优化技术.本文提出的基于t分布变异的蝙蝠算法，由于引入t分布变异策略增加了种群的多样性，有利于算法跳出局部最小值的束缚，因此加快蝙蝠算法的收敛速度，提高了解的质量.由仿真实验结果可以看出，该算法的性能在不同程度上优于其他优化算法.

［1］ YANG X S.A new metaheuristic bat－inspired algorithm［M］.Nature Inspired Cooperative Strate－gies for Optimization.Bristol：Lunivers Press，2010：97－104.

［2］ YANG X S.Bat algorithm for multiobjective optimization［J］.Int J Bio－Inspired Computation，2011，3（5）：267－274.

［3］ YANG X S，GANDOMI A H.Bat algorithm：A novel approach for global engineering optimization［J］.Engineering Computation，2012，29（5）：267－289.

［4］ FISTER J I，FISTER D，YANG X S.A hybrid bat algorithm［J］.Elektrotehniski Vestnik，2013，80（112）：1－7.

［5］ WANG G G，GUO L H.A novel hybrid bat algorithm with harmony search for global numerical optimization［J］.Journal of Applied Mathematics，2013，65（20）：1－21.

［6］ 贺兴时，丁文静，杨新社.基于模拟退火高斯扰动的蝙蝠优化算法［J］.计算机应用研究，2014，31（2）：392－397.

HE Xingshi，DING Wenjing，YANG Xinshe.Bat algorithm based on simulated annealing and gaussian perturbations［J］.Application Research of Computers，2014，31（2）：392－397.

［7］ LIU Y，LIN G G，YAO X.Evolutionary programming made faster［J］.IEEE Transactons on Evolutionary Computation，1999，3（2）：82－102.

［8］ FARITHA B A，CHANDRASEKAR C.An optimized approach of modified bat algorithm to record deduplication［J］.International Journal of Computer Applications，2012，62（1）：10－15.

［9］ 王波.基于自适应t分布混合变异的人工鱼群算法［J］.计算机工程与科学，2013，35（4）：120－124.

WANG Bo.Artificial fish－school algorithm based on adaptive t distribution mixed mutation［J］.Computer Engineering＆Science.2013，35（4）：120－124.

［10］ 盛孟龙，贺兴时，王慧敏.一种改进的自适应变异蝙蝠算法［J］.计算机技术与发展，2014，24（10）：131－135.

SHENG Menglong，HE Xingshi，WANG Huimin.An improved algorithm for adaptive mutation bat［J］.Computer Technology and Development，2014，24（10）：131－135.

［11］ 刘佳，刘丽娜，李靖，等.基于模拟退火算法的人工鱼群优化研究［J］.计算机仿真，2011，28（10）：185－198.

LIU Jia，LIU Lina，LI Jing，et al.Research of improved artificial fish swarm algorithm based on simulated annealing algorithm［J］.Computer Simulation，2011，28（10）：185－198.

［12］ UI KABIR Md Was，MOHAMMAD S A.Bat algorithm with self－adaptive mutation：A comparative study on numerical optimization problems［J］.International Journal of Computer Applications，2014，100（10）：7－13.

编辑：校对：田 莉

Bat algorithm based on t distribution mutation

CHANG Qing，HE Xingshi

（School of Science，Xi′an Polytechnic University，Xi′an 710048，China）

In order to improve the performance of algorithm，a Bat algorithm based on t distribution mutation（TMBA）is presented.This improved algorithm executes the Gauss mutation on the excellent bat and executes the adaptivet distribution mutation on the nonexcellent bat.The proposed algorithm shows good exploitative properties at the early evolution and more explorative at later evolution process.It uses BA，ABA and TMBA to carry out numerical experiments for 6test benchmarks.The simulation results show that the proposed TMBA is superior to BA and ABA.

Bat algorithm；t distribution mutation；Gauss mutation

TP 18；TP 301.6

A

1674－649X（2015）05－0647－07

10.13338／j.issn.1674－649x.2015.05.023

2015－01－22

陕西省自然科学基础研究计划项目（2014JM1006，2014KRM28－01）；陕西省教育厅专项科研计划项目（14JK1282）

贺兴时（1960—），男，陕西省富平县人，西安工程大学教授，研究方向为智能优化算法、数理统计、数据挖掘等.E－mail：xingshi－he＠163.com