基于结构分析的软件可靠性评估代数方法
2015-06-05刘广亮
张 捷,陆 阳,刘广亮
(1.合肥工业大学计算机与信息学院,安徽合肥230009;2.安徽师范大学数学计算机科学学院,安徽芜湖241003)
基于结构分析的软件可靠性评估代数方法
张 捷1,2,陆 阳1,刘广亮1
(1.合肥工业大学计算机与信息学院,安徽合肥230009;2.安徽师范大学数学计算机科学学院,安徽芜湖241003)
针对含有多种结构风格的复杂软件系统,提出一种可靠性评估代数方法。该方法基于软件体系结构代数建模思想,通过分析构件间交互的特点,使用代数范式形式抽象软件的基本结构风格。明确了范式向系统状态空间的映射关系,由此建立可靠性参数计算准则,并实现了系统可靠性评估的完整流程。因为代数语言的高度形式化特征,流程具有结构嵌套处理以及自动完成计算的显著优点。最后通过对一个实际软件系统的可靠性分析,验证了代数方法的适用性与有效性。
软件可靠性;系统可靠性;软件结构风格;复杂软件系统
0 引 言
可靠性是软件的重要质量指标之一。过去数十年间,对软件系统可靠性的研究主要集中于如何有效地建立可靠性模型,以及从模型出发如何准确地评估系统的可靠度。目前此领域的主流方法分为两类:一类是基于软件测试期间所获得的失效数据而建立的可靠性增长模型(software reliability growth model,SRGM)[12];另一类是在系统设计阶段建立的基于结构的软件可靠性模型(architecture-based software reliability model,ABSRM)[34]。SRGM类方法认为随着软件测试的进行,软件系统的故障会被不断检出并修复,从而使整个系统的可靠性具有不断增长的特性。以G-O模型、J-M模型及对数泊松分布模型等为代表的SRGM已经广泛应用在软件测试阶段的可靠性评估与预测中,成为开发后期衡量软件项目质量的重要依据。
随着软件设计思想的演变,聚集大量可重用构件(同组件)成为软件开发的趋势,这使得ABSRM开始出现并逐渐成为软件可靠性研究的重要方向。ABSRM类方法相较于SRGM类,最大的不同在于它是白盒方法(而SRGM通常认为是黑盒方法),考虑了软件内部结构的信息,模型建立在软件开发的早期阶段,这使得可靠性评估在软件设计阶段就可以进行,对避免在开发后期因结构设计不当而返回修改所产生的代价有着重要意义,而这种代价往往是巨大的。
Littlewood B首先在文献[5]中使用半马尔可夫过程(semi-Markov process,SMP)对软件结构建模,并率先提出构件可靠性和构件间控制转移概率是决定系统可靠性的两个关键因素。随后Cheung R C于文献[6]给出了他的重要模型,这一模型基于离散时间马尔可夫链(discrete time Markov chain,DTMC),结构中含有吸收态(相对于SMP它是可约的),将系统成功执行的概率刻画为从初始构件转移到结束构件的概率,解决了系统可靠性与构件可靠性及构件间控制转移概率的函数关系问题。基于DTMC更好的描述性质,他推导出单个构件可靠性对系统可靠性的敏感度公式,用以刻画关键位置构件的可靠性变动对整个系统可靠性的影响程度。而Laprie J C[7]使用连续时间马尔可夫链(continuous time Markov chain,CTMC)将构件执行时间均值作为参数引入模型,用以反映系统执行稳态。这之后出现的ABSRM类方法基本都遵循这一路线。
软件规模在不断增长,软件结构中所呈现的复杂性也在迅速增加。在Cheung R C的经典模型中[6],仅讨论了含有顺序 分支单一结构风格的简单软件系统,这显然已不适合当前复杂软件结构的需要。对此Wang W L等[8]讨论了若干种特设软件结构下的具体可靠性评价方法。Liu C等[9]提出混合软件可靠性模型概念,增加了调用 返回结构风格。之后,王强等[10]又增加了并行、中断冗余和容错结构风格,并分析了这些基本软件结构风格在可靠性评价中的普适性。同时,一些学者也从描述能力上对ABSRM类方法进行改进。如陆文等[11]使用Petri网描述软件体系结构,并基于此分解和计算复杂软件系统的可靠性。赵会群等[12]使用抽象代数工具和体系结构描述语言(architecture description language,ADL)来描述构件间的依赖关系,使结构风格得以抽象化,并据此提出可靠性范式的概念,他在SMP模型中证明了该范式的正确性。
软件结构的复杂性在于基本结构风格的多样性,并且新的结构风格仍在不断产生[89,13]。ABSRM类方法需要不断扩充和调整以适应这些新增的结构风格。同时注意到,目前的ABSRM方法尚不能处理基本结构的嵌套问题。文献[10]比较完整地讨论了若干类基本结构风格的可靠性计算方法,但是并没有涉及由基本结构嵌套组合形成的复杂子结构的可靠性计算问题,而这种复杂子结构在软件体系结构设计中经常出现。本文使用文献[10]中对软件基本结构的分类,立足于在较高的抽象层上对软件系统体系结构作形式化描述,原因有二:一是新的结构风格的增加在抽象层上并不一定需要增加新的描述方法以适应;二是形式化方法往往具有描述结构嵌套的能力。
另一个问题是对复杂软件的可靠性评估计算是否可以自动完成。对比最近出现的典型ABSRM类模型或方法[8,1417]可以发现,它们无一例外都是对目标系统直接建立马尔可夫链(DTMC或CTMC),之后手工计算出整个系统的可靠度。这一过程势必会随着软件系统规模的增加而愈发困难。文献[18]使用了统一建模语言(unified modeling language,UML)对可靠性模型进行转换,通过引入UML记号使其具备自动计算的能力。但其转换而成的模型过于臃肿而不易用,需要一整套UML环境和工具的支持,并且该模型仍缺乏对可泛用的基本结构风格以及结构嵌套的描述。在软件开发早期,特别是在体系结构设计阶段,如果伴随每一次结构的修改都能实时自动地计算出最终整个系统的可靠度,这无疑十分有益于设计者的正确决策。
针对以上,本文的工作主要有:
(1)使用代数方法对软件体系结构建模,模型以代数表达式集合的形式体现。这些表达式或为范式(用以表达基本结构风格),或为范式的嵌套组合(用以表达复杂子结构)。
(2)定义基本结构范式向状态空间的映射关系,并给出其可靠性计算方法。
(3)给出自动解析代数表达式集合的流程,依据映射关系计算生成系统状态随机转移矩阵,并据此计算出整个系统的可靠度。
代数模型对软件体系结构的描述准确而简洁,本文首先介绍了该模型以及经典的结构分析类软件可靠性模型理论;然后使用代数方法描述不同的软件结构风格,并提出基于代数范式的可靠性计算方法;接着给出整体的可靠性评估流程,该流程可自动完成;最后用一个实例来验证可靠性评估代数方法的有效性。
1 相关工作
1.1 基于结构分析的可靠性评估方法
大多数ABSRM类方法都建立在文献[6]的经典DTMC模型上。该模型假设单个构件的可靠度已知,构件的失效行为彼此独立,而且构件间的控制转移关系满足马尔可夫性质,即转移目标仅取决于当前执行构件。图1给出了由10个构件组成的控制转移图。图中每个结点Ci表示一个单独构件,其可靠度为常量Ri。有向弧〈Ci,Cj〉表示一个可能存在的由Ci至Cj的控制转移,用pi,j表示该转移的发生概率。定义一步随机转移矩阵如下:

式中,Q为n×n矩阵,其中元素Q(i,j)=Ri·pi,j,表示系统在构件Ci无错执行后成功转移至Cj的概率。注意到若弧〈Ci,Cj〉本身并不存在,则pi,j为0。

图1 构件控制转移图
考虑Q的k级幂Qk,即k步转移矩阵,则其元素表示由Ci经过k步成功到达Cj的概率。令Neumann级数

式中,I表示单位矩阵。则N(i,j)表示所有经由Ci出发经过若干步成功到达Cj的概率之和。据此,整个系统的可靠度可由下式计算:

即理解为系统由初始构件C1出发经过若干步成功到达终止构件Cn,并成功执行Cn的概率。
易知矩阵Q的谱半径ρ(Q)<1,故级数N收敛,于是有


需要指出的是,文献[6]的模型中构件间的相互关系只有顺序-分支一种,而且假设单个构件可靠度固定不可变动的做法也忽略了系统操作剖面信息等带来的影响,这之后出现的模型和方法都对此做出了很多改进。
1.2 网构软件体系结构代数模型
有研究表明,使用代数理论建立的体系结构模型,通常具有高度的形式化特征,易得出量化分析结果,这为在开发早期阶段分析系统的可靠性、可维护性、可演化性及可复用性等非功能性属性方面提供了可能[21]。本文采用文献[22]中提出的网构软件体系结构代数模型。它的优势在于:
(1)使用代数算子抽象软件体系结构中的连接子,使得对软件结构的描述具有高度抽象的形式化特征;
(2)相对于进程代数,该模型理论使用的代数语言更加简洁,易于扩充,而且模型含义准确清晰,便于后续进行可靠性相关分析。
为叙述扼要,这里只列出代数模型的定义。
定义1[22]设论域为U,一个U上的软件体系结构是三元组<C,O,Ω>,其中C为构件集合,O为所使用连接子集合,Ω为确定的体系结构风格。
代数模型中的连接子形式上表现为代数算子,分别有:“激发”⊕,“使用”⊗,“选择”+和“协同”Θ。设有构件A,B∈C,表达式A⊕B由构件和算子组成,它的涵义为构件A对构件B进行了一次激发,反映了构件间最基本的一种交互方式。激发动作完成后,系统的控制状态将由A传递到B。根据构件间交互方式的不同,补充了算子“并行”‖、“冗余”Δ和“中断容错”Ψ。关于这些算子,第2节会在基本结构范式中逐个讨论它们的作用机制。
称表达式A⊕B为激发运算范式,记作Role=A⊕B。而集合Ω是由若干Role组成,即为一个表达式的集合。
用一个实际算例来说明代数模型如何描述实际的软件体系结构。该算例来自文献[10],属于安全关键系统,其中含有10个构件模块,图2给出了它们之间的控制转移关系。C1是初始模块;C2与C3分别对应两类不同的功能模块,它们都需转移至核心业务模块C4;C5作为C4的一个中断容错而存在,功能完全等同于C4,仅当C4出现故障时才接管进程;核心模块下达的一部分任务会被分解并交由C6与C7并行处理,另一部分任务交由C8处理;而C6、C7和C8都需要使用业务模块C9提供的功能;最终结果需经由输出模块C10处理。
1848年,欧米茄创始者路易士·勃兰特开设了自己的制表公司,自那时起,他始终致力于生产精准的机心。1894年,勃兰特兄弟制造出19令机心,并命名为“欧米茄”。这一革命性机心在行业内广受赞誉,“欧米茄”也因此成为了公司的品牌名称,寓意着“完美、卓越与成就”。

图2 算例构件控制转移图
对该实例,如果只采用文献[6]的DTMC模型来求解系统可靠性,构件间的所有交互关系都将被处理为顺序-分支结构,即图2中所有的有向弧都被认为是控制转移。如前文所述,显然这并不合理。例如C2与C5之间的控制转移多数情况下并不会发生,仅当C4失效时才会发生。而C5作为C4的一个容错备份,这一关系并不能在图2中得到直接体现,从而忽略了设计时它们之间确实有连接子存在的事实。C6与C7亦是如此。当然也可以在构件控制转移图上添加记号以注明这些构件间的某种连接子的存在,但是不妨换一种思路,如果一开始就使用代数模型的方法进行体系结构设计会如何。
根据定义1,该算例的的代数模型描述如下:

在集合Ω中,只使用了7个表达式就足以描述结构设计意图。这些表达式中使用了括号,清楚表明了子结构之间的嵌套层次和组合关系,如此便很自然地解决了复杂子结构嵌套的描述问题。如表达式Role4=(C4ΨC5)⊕(C6‖C7+C8),它反映了两个子结构之间的控制传递关系。子结构C4ΨC5为基本的中断容错运算范式,而子结构C6‖C7+C8则是复杂表达式,表明了控制流在并行运算块C6‖C7与C8之间的分支选择关系。根据耦合度的高低,这里认为算子‖的优先级大于算子+。事实上,选择运算是耦合度最低的,在对代数模型的后续处理中,需要将选择运算展开。
定理1[22]激发运算对选择运算满足分配律,即

证明见文献[22],这里略去。
根据定理1,Role4可以展开为(C4ΨC5)⊕(C6‖C7)和(C4ΨC5)⊕C8两个式子。
显然Ω中的代数表达式属于形式语言范畴,可以使用形式语言的语法分析技术来对它们进行解析。可以证明由有限个算符加上括号所构成的表达式符合上下文无关文法,采用通用的LR分析算法即可完成对这些表达式的扫描与识别。本文第3节给出解析表达式集合Ω的流程,其目的在于最终生成类似第1.1节的一步随机转移矩阵,以计算出整个系统的可靠度。
2 基本结构风格范式的可靠性计算
代数模型是对软件体系结构的高度抽象,能够准确地描述构件间的交互机制。在代数模型设计完成后,需要有一套可靠性计算的准则。这一准则从基本的软件结构风格出发,形式上表现为由不同代数算子构成的运算表达式,称之为基本结构风格范式。计算准则必须是可泛用的,所以范式必须足够精简,即不能再被继续展开。
本节讨论几种不同的风格范式,基本涵盖了目前在ABSRM类方法中出现的软件结构风格。对这些范式的可靠性计算,使用形如

的映射来完成。式中C为构件集合,而S为系统状态结点集合。状态结点Si∈S可能对应单个构件,也可能对应若干构件的组合,当系统处于某个状态结点上时,控制转移不会发生,即认为系统处于一个相对稳定的可靠性水平上。
映射^f的主要功能有两个:一是生成相关状态结点并计算其可靠性参数;二是生成或者更新一步随机转移矩阵Q中的元素。矩阵Q形式上等同第1.1节的随机转移矩阵,只是这里的行列坐标对应状态结点而非构件。
下文将从基本的软件结构风格出发,分别给出它们对应的结构风格代数范式,以及这些范式的可靠性计算方法。
2.1 顺序 分支结构
顺序 分支结构是最简单的软件结构风格。如图3(a)所示,构件C1发出的转移可在由C2到Ci的若干构件中进行选择。任一时刻只有当前构件在执行,执行完成后才会转移到后续构件。在代数模型中,激发运算是表示控制转移动作的唯一运算,该运算有严格的前后逻辑关系故不满足交换率。可以将图3(a)的结构描述为

显然,括号内选择运算用以描述多分支的情况。由定理1,上式可以展开为多式,表示各条由C1到达Cn的不同路径。当表达式中仅含有激发和选择算子时,每个构件都应对应一个系统状态结点,如图3(b)所示。

图3 顺序 分支结构
实际使用代数模型时,为了便于后续操作不建议把表达式写成上述连续激发的形式,而应是从左至右两两组成一个双目运算表达式。设有激发运算范式

式中,A,B∈C;Role1为该范式标记(下同)。记p(Role1)=pA,B,以表示该激发范式的发生概率参数,等同于构件A向构件B的控制转移概率。
对双目表达式Role ,定义映射

(1)对应构件A,B生成状态结点SA,SB,若所输入构件在集合S已存在对应结点,则不需生成新的结点。
(2)更新状态结点的可靠性参数

式中,υ(A),υ(B)表示构件的执行频度数学期望值。
(3)更新一步随机转移矩阵Q中的元素

特别地,认为激发运算是唯一导致控制转移的运算,对应系统状态的变迁。函数被定义为只能处理双目运算的情形。代数模型在设计时,应当将所有激发运算写成双目而非多目的形式,以便于处理p(Role)参数。
2.2 调用 返回结构
此结构风格指当前构件为完成某一任务而需调用其他构件的功能。如图4(a)所示,C1调用C2完成任务后,再将控制传递给C3。需要指出的是,传统的过程调用并不满足面向构件设计典范,因为这将导致构件实现非独立,从而不能满足DTMC模型的失效独立假设[8]。

图4 调用 返回结构
图4(a)的结构关系可以描述如下:

式中,C1⊗C2反映了C1与C2间的调用关系;⊗为使用运算的算子,称C1对C2构成一个使用运算。
设有使用运算范式
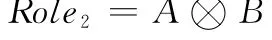
为满足失效独立假设,需要对Role2作如下演化处理:

式中,X表示所有被A所激发连接的构件或子式。在图4(a)的情形下,X即为构件C3。而B′表示当前执行构件A在完成对B的正确调用并返回后,所到达的结点,该结点位于A内部,称B′为A的内部结点,它的可靠性参数与A相同。
对演化式Role21,定义映射

其工作有:
(1)对应A,B′生成状态结点SA,SB′。
(2)更新可靠性参数RSA=RSB′=Rυ(A)A。
(3)更新矩阵元素

式中,p(Role21)=p(Role2),即Role21式的发生概率参数与原式相同。注意到由状态结点SA成功到达SB′,仅与构件B的成功执行和调用关系的发生概率有关,反映了SB′实际仍处在当前执行构件是A的状态。
因为X可能不唯一,故Role22式可能不只一个。其发生概率参数p(Role22)=1,表明到达内部结点所处的状态后,系统状态将无条件向所有可能的后续状态转移。新增的Role22式仍使用映射函数^f1处理。
图4(a)中的调用结构在演化完成后新增加二式

式中,C′2为内部结点。图4(b)给出了演化后所对应的状态结点转移关系。
2.3 并行结构与协同结构
将并行结构与协同结构放在一起考虑,在代数模型中分别对应并行运算与协同运算。如图5(a)所示,当前执行构件C1会将任务交由构件组C2C3…Ci共同完成。构件组内若是并行连接,则描述为

若是协同连接则描述为

并行与协同结构的区别在于:并行结构是任务先分解成子任务交由构件组内的每个构件独立完成,之后合并子任务形成结果;而协同结构是任务的执行需要构件组内相互协作完成,中间可能需要构件间相互激发多次。相同点在于任务执行时若组内某个构件失效,则整个任务失败。故构件组对应一个系统状态结点,图5(b)反映了这一点。

图5 并行/协同结构
设有并行运算范式

和协同运算范式

对二式定义映射

处理,f^3的工作有:

2.4 中断容错结构
此结构指当前执行构件失效时,系统将启动中断机制将控制权收回,转而传递到备份构件继续执行相同的任务。如图6(a)所示,当执行构件C2失效时,控制权将由C1收回,并转而交由C2的一个备份C3。若C3仍失效,则交由C4执行,…,直到所有的备份构件都失效,则任务失败。中断容错结构具备很强的错误恢复能力,适用于可靠性要求较高的软件系统。代数模型中,使用算子Ψ来表示这一结构,图6(a)可描述为


图6 中断容错结构
设有中断容错范式

对Role5,定义映射

其工作有:
(1)仅生成一个状态结点SA。
(2)更新可靠性参数

式中,n为范式中的构件数目。
如图6(b)所示,结构(C2ΨC3Ψ…ΨCi)仅对应了一个状态结点,但其可靠性程度显然大于单个构件C2独立完成任务的情形。
2.5 冗余结构
最后讨论的是冗余结构风格,它兼顾了可靠性与实时性的双重要求。如图7(a)所示,在同一时间内共有n个完全相同的构件C2在执行相同任务,n个C2有可能都成功执行,也有可能都失败。设在n个构件中若至少有m个成功(通常取m≥n/2),则整体冗余结构执行成功,否则认为是失败。用算子Δ表示冗余关系,图7(a)可描述如下:


图7 冗余结构
设有冗余范式

由n个A连接而成。对Role6,定义映射

其工作有:
(1)仅生成一个状态结点SA。
(2)更新可靠性参数

其中,n/2≤m≤n。
3 代数模型的可靠性评估
第2节中,对不同的软件结构风格,分别给出了相对应的代数范式描述,并定义了映射~在系统状态空间上计算这些范式的可靠性参数。基于此,本节将讨论一个完整的体系结构代数模型的可靠性评估方法,有如下的流程。
代数表达式属于形式语言范畴,对表达式集合Ω的扫描与识别基于形式语言的语法分析技术。在输入信息完整的前提下,上述流程可自动完成对整个系统可靠度的计算。这些信息包含:单个构件的可靠度和执行频度值、构件间的控制转移概率。
回到第1.2节中的算例。该例中存在使用运算的情况

而使用运算不符合ABSRM理论的构件间失效独立假设,故需要对这一类表达式作预处理。同时,为了简化后续处理,需要将Ω中的所有选择运算展开。如

将被展开为C1⊕C2与C1⊕C3两个式子,以便于处理构件间的控制转移概率。算法1给出了预处理的过程。
算法1代数模型预处理
输入<C,O,Ω>
输出<C′,O′,Ω′>
初始化C′=C,O′=O,Ω′=Ω
步骤1从Ω中取表达式Rolei,若Rolei中含有选择算子,则将其展开为

的形式。Ω′中增加Rolei1,Rolei2,…,Ω′中删除Rolei。
步骤2重复步骤1直至取完所有表达式。
步骤3O′中删除算子+。
步骤4从Ω中取表达式Rolei,若Rolei含有使用算子,则对其演化。Ω′中增加演化式Rolei1(需标记)与Rolei2,Ω′中删除Rolei,C′中增加内部结点Bi。
步骤5重复步骤4直至取完所有表达式。
步骤6O′中删除算子⊗。
经过算法1的预处理后,该算例的代数模型如下:

注意到O′已经不包含使用和选择算子,C′中增加了内部结点B1,B2,而Ω′中增加了由使用表达式演化的Role7、Role8、Role9与Role10。Role7与Roel9均已标记,以表明它们区别于其他的激发表达式,需使用映射单独处理。
对于Role5=(C4ΨC5)⊕(C6‖C7)这样的嵌套表达式,语法分析器会按算符优先级先从括号内开始解析。按结构耦合程度的高低,算子‖、Θ、Δ与Ψ处于同一级,它们优先于算子⊕处理。同时,为了避免二义性,并行、中断容错与冗余结构在实际描述时应加以括号。考虑如下式子:

其可理解为子结构AΘB与C的并行连接,也可理解为A与子结构B‖C的协同连接,这样便产生了二义。故应当加以括号,例如写成

的形式,以确保所描述结构是确定无歧义的。

算法2状态结点及转移矩阵生成
输入<C′,O′,Ω′>
输出S,Q
初始化建立n×n的零矩阵Q,n是C′中构件的数目。
步骤1从Ω′中取表达式Rolei,若Rolei含有并行/协同、中断容错及冗余子式,则对应使用映射及处理子式,生成状态结点Si,以结点Si替换子式。
步骤2重复步骤1直至取完所有表达式。
步骤3从Ω′中取表达式Rolei,若Rolei为标记的演化式,使用^f2处理,否则使用处理,生成状态结点并更新矩阵Q中对应元素。
步骤4重复步骤3直至取完所有表达式。
在步骤1中,一个LR分析器负责扫描与识别是否存在括号及相关算子。限于篇幅,这里不再叙述形式语言的LR分析算法。步骤1中会以生成的状态结点替换括号所表达的子式,以保证在步骤3开始时Ω′中只存有激发表达式。另外,仅在步骤3中才会更新矩阵Q的元素,符合只有激发运算才会进行构件间控制转移的事实。考虑到所有构件都可能对应一个状态结点的情形,Q被初始化为n×n的矩阵,它的行列坐标初始时都对应一个构件,最终生成的Q中,可能有些行和列仍全为0并没有被更新,因为可能出现多个构件仅产生一个状态结点的情形,例如一个并行结构中的构件。
在软件开发的早期,使用代数方法设计软件体系结构模型时,根据本节提出的流程可实时、自动地计算出模型的整体可靠度。而以往的ABSRM类方法并不能伴随设计过程进行可靠性的自动计算,这是代数方法的形式化描述能力所带来的优势。
4 有效性验证
表1给出了第1.2节中算例的单个构件可靠度、执行频度,以及构件间控制转移概率。该算例属于工业安全关键系统,经实际测试,其可靠度估计值为0.865[10]。需要说明的是,以上数据来自系统实际运行时的模块检测及失效数据,可以认为是系统的稳定属性参数。

表1 构件可靠度、执行频度及控制转移概率
该软件系统早于网构软件体系结构代数模型出现,故没有原始的代数模型设计。已在第1.2节中给出了它的代数模型<C,O,Ω>,并在第3节给出预处理后的<C′,O′,Ω′>。
基于第2节中讨论的计算准则,代数模型在使用算法2后,生成如下系统状态一步随机转移矩阵:

注意矩阵Q已删去了顺序位置相同并且全为0的行和列,因为这些行和列并不对应实际的状态结点。矩阵Q的行列坐标实际对应状态结点集合如下:点 对应子结构 ;结点 对应子结构

式中,结S4C4ΨC5S5C6‖C7;而S6与S8则对应了两个演化式中的内部结点。
表2列出了算例的代数模型经过预处理后,在算法2处理流程中需要计算的相关可靠性参数。可以看出,系统状态结点与构件并非一一对应,可能出现多个构件对应一个状态结点的情况。而状态结点可靠度R的计算受到所涉构件可靠度、执行频度及结构风格类型等多个因素的影响。

表2 可靠性评估流程中的相关参数
图8明确表示了最终生成的状态结点之间的转移关系。其中系统的初始状态为结点S1,当经过若干步状态迁移到达状态结点S9,并成功执行S9所对应的构件模块后,即认为完成了整个系统的一次成功执行。

图8 算例系统状态结点关系图
依据所得矩阵Q和式(2)、式(3),系统可靠度计算如下:

表3列出了几种主流ABSRM类方法对该算例的可靠性评估值,计算平台为Matlab 6.0。

表3 各建模方法可靠性评估值比较
对比可以看出,文献[6]的模型因为忽略了软件结构风格的影响,对该软件系统的评估结果不理性(0.820 8)。文献[9]的模型优势在于能够处理确定性转移与概率性转移两类结构,但仍然无法准确反映更多的结构风格,故结果较差(0.814 7)。而文献[10]与文献[11]的建模方法评估结果与实际较接近,其中文献[10]引入了更多的软件结构风格,而文献[11]则使用了Petri网以增强模型对结构和执行路径的描述能力。使用本文的代数方法得到的结果比较理想(0.858 2),与实际评估值的误差仅在1%以内,说明此方法是有效的。
5 结 论
形式化方法一直是软件及系统工程理论中的研究热点。在软件可靠性评估中引入代数方法,其优势在于对软件基本结构风格的准确描述能力。本文的贡献在基于代数范式构建了完整的可靠性计算准则与流程,使得软件模型的可靠性评估可伴随模型设计同时进行,这无疑在软件开发早期有着重要的意义,设计人员可随时评估模型的更改对整体可靠性带来的影响,从而有效避免在开发中后期因结构设计不当等早期缺陷而导致的延误。下一步,考虑在软件的演化和动态结构更改对可靠性的影响方面对该代数方法作出改进。
[1]Lyu M R.Handbook of software reliability engineering[M].New York:McGraw-Hill Press,1996.
[2]Musa J D.Software reliability engineering[M].New York:McGraw-Hill Press,1998.
[3]Gokhale S S,Trivedi K S.Analytical models for architecture-based software reliability prediction:a unification framework[J].IEEE Trans.on Software Engineering,2006,55(4):578- 590.
[4]Gokhale S S.Architecture-based software reliability analysis:overview and limitation[J].IEEE Trans.on Dependable and Secure Computing,2007,4(1):30- 40.
[5]Littlewood B.Software reliability model for modular program structure[J].IEEE Trans.on Reliability,1979,28(3):241- 246.
[6]Cheung R C.A user-oriented software reliability model[J].IEEE Trans.on Software Engineering,1980,6(2):118- 125.
[7]Laprie J C.Dependability evaluation of software systems in operation[J].IEEE Trans.on Software Engineering,1984,10(6):701- 714.
[8]Wang W L,Wu Y,Chen M H.Architecture-based software reliability modeling[J].Journal of Systems and Software,2006,79(1):132- 146.
[9]Liu C,Liu B,Ruan L.A reliability model based on heterogeneous software architecture[C]∥Proc.of the 8th International Conference on Reliability,Maintainability and Safety,2009:728- 732.
[10]Wang Q,Lu Y,Fang H,et al.Complex software reliability evaluation method based on architecture analysis[J].Journal of Systems Engineering,2013,28(2):271- 284.(王强,陆阳,方欢,等.基于结构分析的复杂软件可靠性评估方法[J].系统工程学报,2013,28(2):271- 284.)
[11]Lu W,Xu F,Lv J.An approach of software reliability evaluation in the open environment[J].Chinese Journal of Computers,2010,33(3):452- 462.(陆文,徐锋,吕建.一种开放环境下的软件可靠性评估方法[J].计算机学报,2010,33(3):452- 462.)
[12]Zhao H Q,Sun J,Wang G R,et al.Reliability model of component based software system[J].Mini-Micro System,2002,23(8):950- 954.(赵会群,孙晶,王国仁,等.基于组件的软件可靠性模型[J].小型微型计算机系统,2002,23(8):950- 954.)
[13]Malek S,Mikicrakic M,Medvidovic N.A style aware architectural middleware for resource-constrained,distributed systems[J].IEEE Trans.on Software Engineering,2005,31(3):256- 272.
[14]Sato N,Trivedi K S.Accurate and efficient stochastic reliability analysis of composite services using their compact Markov reward model representations[C]∥Proc.of the IEEE International Conference on Services Computing,2007:114- 121.
[15]Sharma V,Trivedi K S.Quantifying software performance,reliability and security:an architecture-based approach[J].Journal of Systems and Software,2007,80(4):493- 509.
[16]Cheung L,Roshandel R,Medvidovic N,et al.Early prediction of software component reliability[C]∥Proc.of the 30th International Conference on Software Engineering,2008:111- 120.
[17]Lipton M W,Gokhale S S.Heuristic component placement for maximizing software reliability[M]∥Pham H.Recent Advances in Reliability and Quality in Design.Berlin:Springer,2008:309- 330.
[18]Brosch F,Koziolek H,Buhnova B,et al.Architecture-based reliability prediction with the Palladio component model[J].IEEE Trans.on Software Engineering,2012,38(6):1319- 1339.
[19]Allen R,Garlan D.A formal basis for architecttural connection[J].IEEE/ACM Trans.on Software Engineering and Methodology,1997,6(3):213- 249.
[20]Alessandro A,Flavio C,Marco B.A process algebraic approach to software architecture design[M].London:Springer-Verlag,2010.
[21]Bernardo M,Inverardi P.Formal methods for software architectures[M].Berlin:Springer-Verlag,2003.
[22]Zhao H Q,Sun J.An algebraic model of internetware software architecture[J].Scientia Sinica(Informationis),2013,43(1):161- 177.(赵会群,孙晶.网构软件体系结构代数模型[J].中国科学:信息科学,2013,43(1):161--177.)
张 捷(198-0-,男,博士研究生,主要研究方向为可信计算、软件与系统可靠性。
E-mail:zjzj2526@hfut.edu.cn
陆 阳(1965- ),男,教授,博士,主要研究方向为计算机控制、传感器网络。
E-mail:luyang.hf@126.com
刘广亮(197-8- ),男,博士研究生,主要研究方向为复杂网络、网络可靠性。
E-mail:homecs@126.com
Algebraic approach of software reliability estimation based on architecture analysis
ZHANG Jie1,2,LU Yang1,LIU Guang-liang1
(1.School of Computer and Information,Hefei University of Technology,Hefei 230009,China;2.School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)
An algebraic approach of reliability estimation is proposed,which aims at the diversity of architecture styles in complex software systems.The approach is built on algebraic modeling for software architecture and analyzes the characteristic of component interaction.It provides abstract algebraic paradigms for basic structures.By setting up the mapping relation between the paradigms and the system states,the computational rules of reliability parameters and a process of the overall assessment for system reliability are established.Because of the formal features of the algebraic method applied,the process has significant advantages in dealing with the nested structure and calculating automatically.Finally,in order to illustrate the applicability and effectiveness of the proposed approach,the reliability analysis of an actual software system is presented.
software reliability;system reliability;software architecture style;complex software system
TB 114.3
A
10.3969/j.issn.1001-506X.2015.11.35
1001-506X(2015)11-2654-09
2014- 06- 16;
2015- 05- 14;网络优先出版日期:2015- 07- 09。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150709.1646.002.html
国家自然科学基金(61070220);教育部博士点基金(20120111110001)资助课题
