基于贝叶斯压缩感知的CSR稳健参数估计方法

代 林，崔 琛，余 剑，梁 浩

（电子工程学院通信对抗系，安徽合肥230037）

基于贝叶斯压缩感知的CSR稳健参数估计方法

代 林，崔 琛，余 剑，梁 浩

（电子工程学院通信对抗系，安徽合肥230037）

针对“完全扰动”情况下压缩感知雷达（compressed sensing radar，CSR）观测矢量和感知矩阵严重失配，进而引起参数估计性能急剧下降的问题，提出了一种基于贝叶斯压缩感知（Bayesian compressed sensing，BCS）的稳健参数估计方法。首先构造“完全扰动”情况下CSR参数估计的稀疏线性模型，并从稀疏矢量的最大后验概率（maximum a posteriori，MAP）出发，推导了完全扰动矩阵服从柯西分布时的优化目标函数；随后通过稀疏矢量和尺度参数的交替迭代，求得稀疏矢量的最优解。与现有重构算法及其改进算法相比，该方法能够有效改善CSR系统应对失配误差的稳健性，提高目标成功检测的概率和参数估计的精度。计算机仿真实验验证了该方法的有效性和鲁棒性。

压缩感知雷达；完全扰动；柯西分布；Lorentzian范数；交替迭代

0 引 言

压缩感知雷达（compressed sensing radar，CSR）是近年来提出的一种新型体制雷达［1］，它将压缩感知（compressed sensing，CS）［2］技术应用到雷达信号处理（radar signal processing，RSP）［34］中，在硬件要求、旁瓣抑制、目标检测和参数估计等方面相比于传统雷达具有显著的优势。CSR在接收端以信息率进行测量感知，无需匹配滤波，降低了系统对硬件的性能要求，经稀疏目标场景的重构进行参数估计，能够同时获得时延和多普勒频率的超分辨估计。

文献［5］指出，测量感知和重构算法的设计构成了CSR研究的主要内容，其中测量感知与测量方式及发射波形有关，重构算法依赖于目标函数的构造和优化求解。如果已知测量方式和发射波形，重构算法的选择或者优化设计就显得尤为重要。然而，现有大多数文献主要针对“加性扰动”（观测噪声）下CSR的参数估计问题进行研究，如迭代重加权最小二乘算法（iteratively re-weighted least squares，IRLS）［6］等，但在实际应用中还存在着“乘性扰动”，它将造成观测矢量和感知矩阵严重失配，导致成功重构的概率显著降低、重构的误差明显增大。文献［7］构造了感知矩阵中存在噪声的“完全扰动”稀疏线性模型，从理论上分析了该模型解的界的问题，并由基追踪（basis pursuit，BP）验证了“乘性扰动”对重构算法的影响。文献［8］推导了上述模型下稀疏信号重构的克拉美罗界（Cramér-Rao bound，CRB）。但M.Herman和Y.Tang都只是针对扰动模型本身展开研究，并没有给出适合求解的重构算法。文献［9］将总体最小二乘（total least squares，TLS）方法应用到重构算法的设计中，提出了适合上述模型优化求解的稀疏TLS（sparse TLS，S-TLS）方法，通过稀疏矢量和扰动矩阵的交替迭代求得稀疏矢量。但是稀疏信号的重构没有限制伪峰的措施，扰动矩阵的求解是已知矢量求矩阵的欠定过程，难以保证求解结果的有效性。类似地，文献［10］采用贝叶斯框架和TLS方法对欠定系统聚焦求解算法（focal underdetermined system solver，FOCUSS）进行扩展，提出了基于总体最小二乘的欠定系统聚焦求解算法（TLS-FOCUSS），在保持FOCUSS收敛性的同时能够处理稀疏线性模型“完全扰动”的情况。文献［11］也针对测量矩阵中存在噪声的情况进行了研究。但是，上述文献都是在完全扰动矩阵服从高斯正态分布的假设下开展研究的，而在实际应用中感知矩阵中包含的噪声更加复杂，更适合采用对称α稳定（symmetric alpha stable，SαS）分布进行描述［12］。这方面的研究见诸报导的还十分有限，主要针对的也是观测噪声服从SαS分布的情况。文献［13］基于Hampel函数和l1范数稀疏正则化，提出了基于M估计的最小化绝对收缩和选择算子（M-estimation-based LASSO，M-LASSO），也称基于M估计的IRLS（M-estimation-based IRLS，Me-IRLS）。当脉冲能量较小时，该算法重构精度较高，但随着脉冲能量增大，估计值的稀疏性急剧恶化。文献［14］选择由Lorentzian范数代替Hampel函数对观测矢量中的异值元素进行回降压缩，提出了基于Lorentzian范数的BP（Lorentzian-based BP，LBP）算法［14］和基于Lorentzian范数的迭代硬阈值（Lorentzian-based iterative hard thresholding，LIHT）［15］算法等两种方法。其中LBP未对重构值中的伪峰进行限制，在较低信噪比条件下的重构误差较大，且计算复杂度较高，无法满足求解效率的要求；LIHT虽然求解效率满足要求，但与IHT一样，需要预知待求变量的稀疏度，且不能从随机投影的观测序列中恢复出待求变量。

针对“完全扰动”情况下CSR参数估计性能急剧下降的问题，本文提出了一种基于贝叶斯压缩感知（Bayesian compressed sensing，BCS）的稳健参数估计方法，与已有算法相比，能够有效改善CSR应对失配误差的稳健性，提高目标成功检测的概率和参数估计的精度。

1 测量矩阵扰动时CSR信号模型

假设远场照射区域内包含Nτ个距离分辨单元和ND个多普勒分辨单元，其中分辨单元（nτ，nD）的时延、多普勒频率和复散射系数分别为，和，不考虑信道衰减，各分辨单元的回波信号在接收端叠加构成CSR的回波信号，有

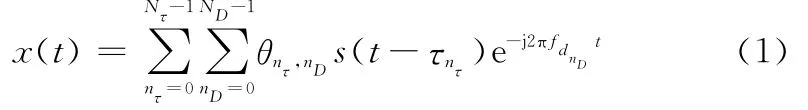
式中，s（t）为发射信号，s＝［s（0），s（1），…，s（Ns－1）］T为离散发射信号矢量，Ns为采样长度。

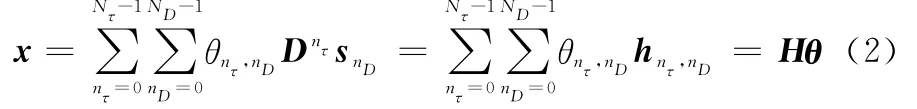
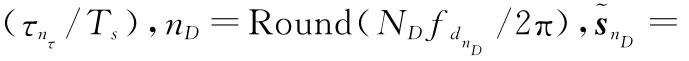
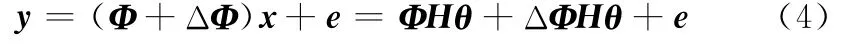
由式（4）可知，ΔΦx是扰动矩阵与回波信号的乘积，将对θ的重构产生“乘性扰动”。令B＝［ΔΦ e］表征CSR系统面临的“加性扰动”和“乘性扰动”，称之为完全扰动矩阵，本文假设B中的每个元素都是零均值独立同分布的SαS随机变量，其特征函数为

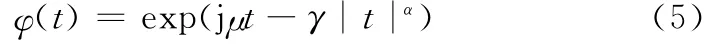
式中，α∈（0，2］为特征指数，决定SαS分布的冲击程度；μ∈（－∞，＋∞）为位置参数，当0＜α≤1时表征SαS分布的中值，当1＜α≤2时表征SαS分布的均值；γ∈（0，＋∞）为分散系数，表征稳定分布中各变量偏离中值或均值的程度。一般情况下，SαS随机变量没有封闭的概率密度函数，无法建立回波信号的贝叶斯模型，难以获得θ的最大后验概率估计。

2 本文算法

根据贝叶斯理论，稀疏信号的重构要求模型具有封闭的概率密度函数，而SαS分布只有在α的值为2、1和0.5时才能满足要求，分别对应高斯正态分布、柯西分布和Levy分布。在高斯分布的假设下，观测矢量中的异值元素将被线性放大，由此获得的估计值可能出现无穷大的偏差；Levy分布的概率密度函数中，指数项和被除项都包含未知量，目标函数难以优化求解；而柯西分布可以大致反映SαS分布在1≤α≤2范围内统计特征，由此建立的目标函数能够有效地避免上述两个问题。因此，下面将以柯西分布为假设前提，构建式（4）中稀疏感知模型的稳健优化目标函数并进行求解。

2.1 目标参数的贝叶斯模型

文献［16］指出，可以认为稀疏矢量θ是独立同分布的广义高斯随机矢量，其最大后验概率估计可以表示为

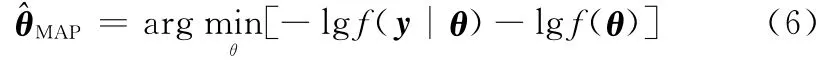
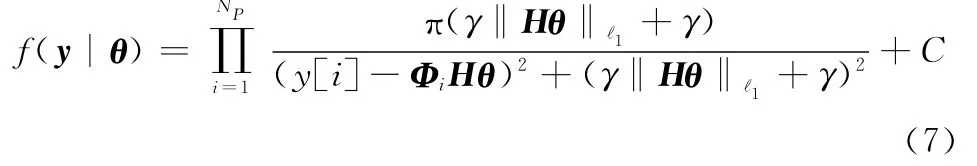
式中，C为常数。将式（7）带入式（6），可得

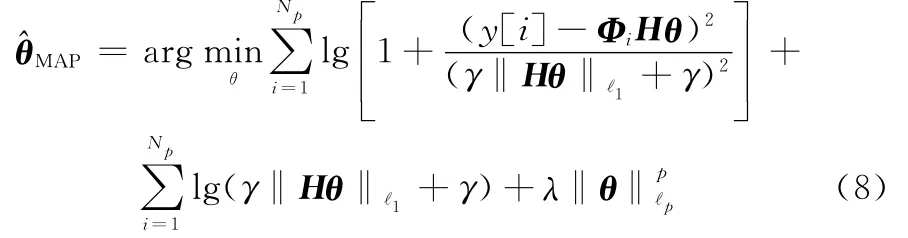
2.2 模型求解

然而，式（8）中的尺度参数包含待求变量，不能直接求解。为此，本文首先利用变量分裂技术［17］进行变换，得到等价的约束优化问题

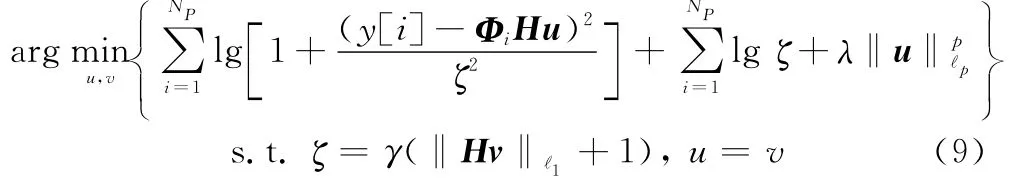
然后，通过交替迭代进行求解，即先固定尺度参数寻找稀疏矢量的估计值，再固定稀疏矢量计算尺度参数的估计值，循环往复，直至收敛。

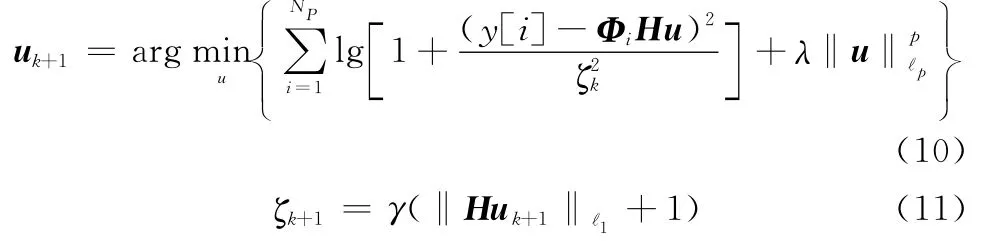
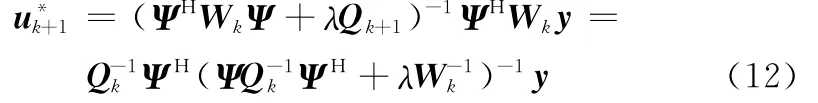
式中，Wk＋1＝W（）和Qk＋1＝Q（）为对角阵，且

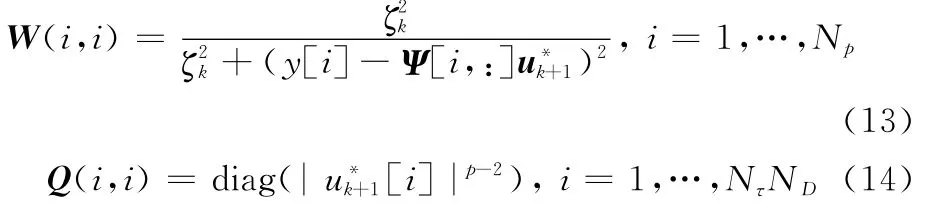
由定点法原理，可以得到式（12）的迭代形式

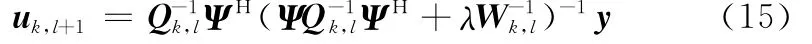
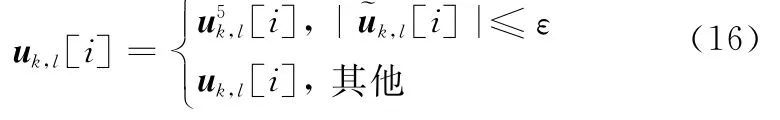
将式（16）中uk＋1带入式（11）以更新尺度参数ζk＋1，重复式（11）和式（16）直到满足终止条件，得到的解即为式（8）中欠定方程的最优解。

3 算法分析

3.1 收敛性证明

定理在迭代过程中，优化目标函数L（θ）是随着迭代次数单调递减的，即L（θk＋1）＜L（θk），其中k为迭代次数。

证明由前面的描述，将L（θ）改写为稀疏矢量u和尺度参数ζ交替迭代的形式，即

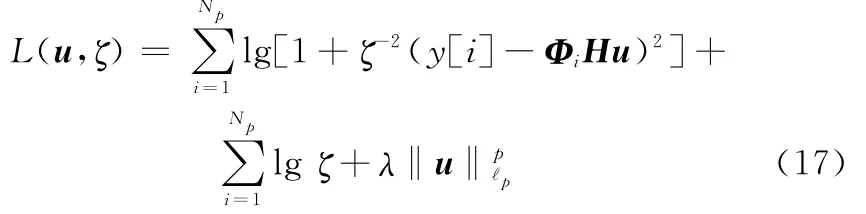
由于L（u，ζ）中包含两个未知变量，必须保证L（u，ζ）关于u和ζ都是减小的，才能证明L（u，ζ）是随着迭代次数单调递减的，即L（θ）单调递减。

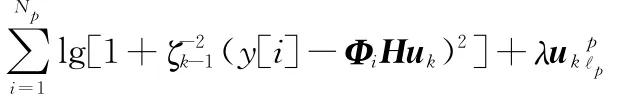
经过l＋1和l次内循环迭代后，可得L1（uk，l＋1）和L1（uk，l），令二者相减，由文献［19］中的推论2和文献［20］中的引理1可得

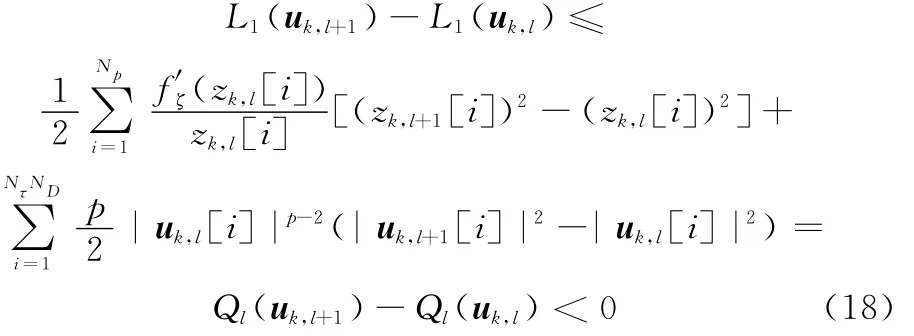
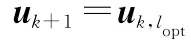
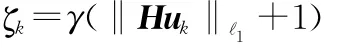
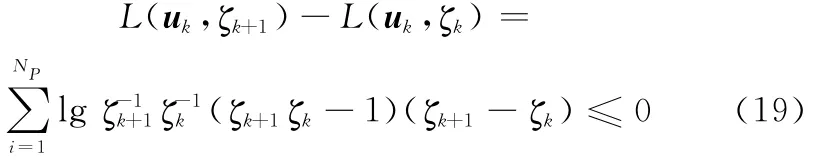
证毕

3.2 算法的计算复杂度

为便于描述，在本小节中记M＝Np和N＝NτND。本文算法的计算量主要在于交替迭代过程中稀疏矢量uk＋1的计算，包括6次矩阵相乘运算，一次矩阵求逆运算，一次矩阵与向量相乘运算和一次标量与矩阵相乘运算，单次迭代需要O（M3＋2NM2＋M2＋4NM＋M）次乘法。此外，式（16）中的阈值收缩有助于提高算法的收敛速率，将进一步降低计算复杂度。S-TLS算法的求解过程包含扰动矩阵的估计，其计算复杂度为O（N3＋N2＋NM2＋4NM）；TLSFOCUSS求解过程包含高维矩阵的特征值分解，计算复杂度为O（（N＋1）3＋（M＋1）（N＋1）2＋2M（N＋1）＋2M2）。

4 仿真实验和数据分析

首先作如下定义：①若估计值中前K个峰值对应着远场照射区域内目标的散射系数，且第K和K＋1个峰值之比大于2.5，则认为目标成功检测，反之不能检测；②估计值的均方根误差（root mean square error，RMSE）定义为

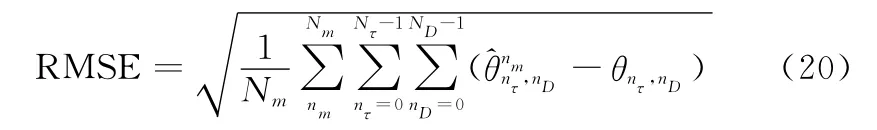
在仿真中，假设CSR载波频率f0＝10 GHz，工作波长λ＝0.03 m，发射信号s为立方码信号，码元长度为Ns＝50；远场照射区内的距离、多普勒分辨单元分别为Nτ＝25和ND＝31，利用（｜x／ND｜，x%ND）可以随机产生分辨单元不同的目标，其散射系数由复高斯分布CN（0，1）产生，其中x⊂［1，NτND］为互不相邻的随机数列，数列中元素的个数代表目标的个数；测量矩阵Φ中的元素都是独立同分布的零均值高斯随机变量且Np＝50。

实验1本文方法的有效性验证。

假设CSR探测区域存在5个目标，位置坐标和散射系数由上文方法产生。图1和图2为完全扰动矩阵服从高斯分布（扰动方差σ2＝0.062 5）和柯西分布（扰动离差γ＝0.025）时，IRLS、LBP、S-TLS、TLS-FOCUSS和本文方法参数估计的结果，图中横坐标“索引值”表示不同的时延－多普勒分辨单元。

由图1和图2可以看出，CSR的参数估计在“完全扰动”情况下受到严重影响。当完全扰动矩阵服从高斯随机分布时，IRLS和LBP的估计值中出现很多伪峰，只能准确地区分出少数强散射目标，如图1（a）和图1（b）；S-TLS、TLS-FOCUSS以及本文方法都可以比较准确地估计出目标的参数，如图1（c）、图1（d）和图1（e）。这是因为，IRLS和LBP在建立优化目标函数时就没有考虑“完全扰动”的情况，不能克服观测矢量的“乘性扰动”；S-TLS、TLS-FOCUSS以及本文方法都是将观测矢量中的“乘性扰动”也作为优化参量，通过各优化参量的交替迭代，降低“乘性扰动”对目标参数估计的影响。

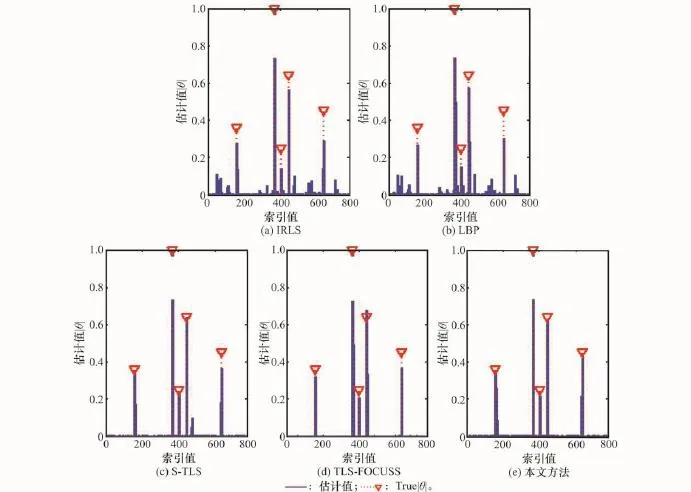
图1 高斯扰动（σ2＝0.25）下，CSR的参数估计结果

当完全扰动矩阵服从柯西随机分布时，IRLS和LBP参数估计的性能进一步恶化，如图2（a）和图2（b）；由于S-TLS和TLS-FOCUSS是在高斯扰动的假设下将TLS思想应用到Lasso和FOCUSS中，对于柯西扰动不具备鲁棒性，目标大多湮没在伪峰中，难以有效区分，如图2（c）和图2（d）；而本文方法则是在柯西分布的假设下，由稀疏矢量的最大后验概率建立优化目标函数，形成类似Lorentzian范数的误差拟合函数，可以有效地抑制观测矢量中的模型噪声和异值元素，如图2（e）。

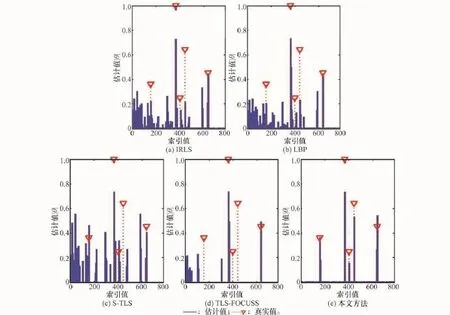
图2 柯西扰动（γ＝0.025）下，CSR的参数估计结果

实验2不同的完全扰动矩阵下，各算法参数估计性能的比较。

假设CSR探测区域存在5个随机分布的点目标，其他参数设置与实验1相同。图3为完全扰动矩阵服从高斯正态分布时，各算法目标成功检测的概率和估计值的RMSE随着扰动方差变化的曲线，不同扰动方差条件下蒙特卡罗实验次数为500。从图中可以看出，在仿真实验限定的范围内IRLS和LBP目标成功检测的概率和估计值的RMSE随着扰动方差的增大而急剧下降；S-TLS、TLS-FOCUSS以及本文方法都具有较好的参数估计性能，其中本文方法目标成功检测的概率介于S-TLS和TLS-FOCUSS之间，估计结果的RMSE略高。这是因为，由于IRLS和LBP未考虑“乘性扰动”，目标的参数估计性能将随扰动方差急剧恶化；与本文方法中的Lorentzian范数相比，S-TLS和TLS-FOCUSS中的l2范数更适合去拟合高斯扰动带来的误差，可以有效克服模型噪声对参数估计的影响，此外，S-TLS由l1范数来衡量稀疏度，仅适用于复散射系数矢量服从拉普拉斯先验分布的情况，而TLS-FOCUSS由广义高斯分布推导构造优化目标函数，利用lp范数可以更准确地刻画复散射系数矢量的稀疏性。

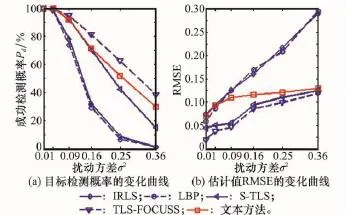
图3 CSR参数估计性能随着扰动方差的变化曲线

图4为完全扰动矩阵服从柯西随机分布时，各算法目标成功检测的概率和估计值的RMSE随着扰动方差变化的曲线，不同扰动方差条件下蒙特卡罗实验次数为500。如果目标不能成功检测，估计值的RMSE视为无穷大。从图中可以看出，LBP可以有效克服离差很小的柯西扰动，当扰动离差γ≥0.02时，IRLS、LBP、S-TLS以及TLS-FOCUSS都难以有效地进行目标的检测，而本文方法在γ≥0.04时仍能保持较高的成功检测概率和估计精度。这是因为，Lorentzian范数是软回降的误差拟合函数，可以有效克服异值元素的影响，由此LBP可以有效克服较小的扰动离差引起的“乘性扰动”，具有一定的鲁棒性；IRLS、S-TLS以及TLS-FOCUSS则在原理上就不能克服观测矢量中的乘性扰动，只有在更小的扰动离差下才具有一定的成功检测概率；本文方法由目标参数的最大后验概率估计建立基于Lorentzian范数的稳健目标函数，通过尺度参数和目标参数的交替寻优，有效去除柯西扰动对参数估计的影响。

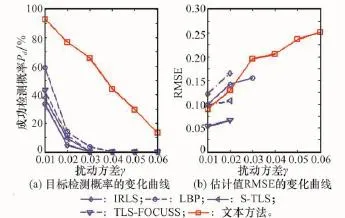
图4 CSR参数估计性能随着扰动离差的变化曲线

图5为完全扰动矩阵服从SαS随机分布（扰动离差γ＝0.025）时，各算法目标成功检测的概率和估计值的RMSE随着特征指数变化的曲线，不同扰动方差条件下蒙特卡罗实验次数为500。从图中可以看出，本文方法在仿真实验限定的范围内（1.0≤α≤2.0）都可以得到较好的成功检测概率和估计值RMSE，而IRLS、LBP、S-TLS和TLS-FOCUSS等算法要求更大的α值；随着α值不断增大，各算法参数估计的性能越来越好，在α＝2.0时可以得到最优的成功检测概率和估计值RMSE。

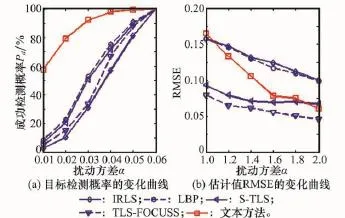
图5 CSR参数估计性能随着特征指数的变化曲线

这是因为，1.0≤α≤2.0范围内的SαS随机分布可由柯西分布近似表征，而本文方法是在柯西扰动的假设下推导而来，理应可以有效克服SαS随机扰动的影响；随着α值逐渐增大，观测矢量中异值元素不断减小，IRLS、S-TLS以及TLS-FOCUSS下被线性放大的元素不断减小，乘性扰动造成的影响越来越小，目标参数的估计越来越准确；当α＝2.0时，完全扰动矩阵服从高斯正态分布，其方差σ＝γ／2，几乎不能对观测矢量产生扰动。

5 结 论

针对“完全扰动”情况下CSR参数估计性能急剧下降的问题，本文提出了一种基于贝叶斯压缩感知的稳健参数估计方法，能够有效改善CSR系统应对失配误差的稳健性，提高目标成功检测的概率和参数估计的精度。与IRLS和LBP等相比，能够有效降低观测矢量和感知矩阵失配对参数估计性能的影响；与S-TLS和TLS-FOCUSS等相比，适用范围可以扩展到由SαS分布描述的完全扰动矩阵。

［1］Baraniuk R，Steeghs P.Compressive radar imaging［C］∥Proc. of the IEEE Radar Conference，2007：128- 133.

［2］Donoho D L.Compressed sensing［J］.IEEE Trans.on Information Theory，2006，52（4）：1289- 1306.

［3］Ender J H G.On compressive sensing applied to radar［J］.Signal Processing，2010，90（5）：1402- 1414.

［4］Strohmer T，Friedlander B.Analysis of sparse MIMO radar［J］.Applied and Computational Harmonic Analysis，2014，37（3）：361- 388.

［5］Zhang J D，Zhang G，Pan H，et al.Optimized sensing matrix design of filter structure based compressed sensing radar［J］.Acta Aeronautica et Astronautica Sinica，2013，34（4）：864- 872.（张劲东，张弓，潘汇，等.基于滤波器结构的压缩感知雷达感知矩阵优化［J］.航空学报，2013，34（4）：864- 872.）

［6］Wipf D，Nagarajan S.Iterative reweighted l1and l2methods for finding sparse solutions［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4（2）：317- 329.

［7］Matthew H，Thomas S.General deviants：an analysis of perturbations in compressed sensing［C］∥Proc.of the IEEE Journal of Selected Topics in Signal Processing，Special Issue on Compressed Sensing，2010，4（2）：342- 349.

［8］Tang Y J，Chen L M，Gu Y T.On the performance bound of sparse estimation with sensing matrix perturbation［J］.IEEE Trans.on Signal Processing，2013，61（17）：4372- 4386.

［9］Zhu H，Geert L，Georgios G.Sparsity-cognizant total leastsquares for perturbed compressive sampling［J］.IEEE Trans.on Signal Processing，2011，59（5）：2002- 2016.

［10］Han X，Zhang H，Meng H.TLS-FOCUSS for sparse recovery with perturbed dictionary［C］∥Proc.of the International Conference on Acoustics Speech and Signal Processing，2011：3952- 3955.

［11］Jiang L B，Huang T.New compressive sampling matching pursuit algorithm［J］.Application Research of Computers，2013，30（2）：402- 404.（蒋留兵，黄韬.一种新的压缩采样匹配追踪算法［J］.计算机应用研究，2013，30（2）：402- 404.）

［12］Shao M，Nikias C L.Signal processing with fractional lower order moments：stable processes and their applications［J］.Pro-ceedings of the IEEE，1993，81（7）：986- 1010.

［13］Zhang Z G，Chan S C，Zhou Y，et al.Robust linear estimation using M-estimation and weighted L1regularization：model selection and recursive implementation［C］∥Proc.of the IEEE International Symposium on Circuits and Systems，2009：1193- 1196.

［14］Carrillo R E，Barner K E，Aysal T C.Robust sampling and reconstruction methods for sparse signals in the presence of impulsive noise［J］.IEEE Trans.on Selected Topics in Signal Processing，2010，4（2）：392- 408.

［15］Carrillo R E，Barner K E.Lorentzian iterative hard thresholding：robust compressed sensing with prior information［J］.IEEE Trans.on Signal Processing，2013，61（17／20）：4822- 4833.

［16］Rao B D，Engan K，Cotter S F，et al.Subset selection in noise based on diversity measure minimization［J］.IEEE Trans.on Signal Processing，2003，51（3）：760- 770.

［17］Li Y F，Feng X C.The split Bregman method for L1projection problems［J］.Acta Electronica Sinica，2010，38（11）：2471-2475.（李亚峰，冯象初.L1投影问题的分裂Bregman方法［J］.电子学报，2010，38（11）：2471- 2475.）

［18］Petersen K B，Pedersen M S.The matrix cookbook［EB／OL］.http：∥matrixcookbook.com.

［19］Carrillo R E.Robust methods for sensing and reconstructing sparse signals［D］.USA：University of Delaware，2011.

［20］Rao B，Engan K，Cotter S，et al.Subset selection in noise based on diversity measure minimization［J］.IEEE Trans.on Signal Processing，2003，51（3）：760- 770.

代 林（198-6- ），男，博士研究生，主要研究方向为压缩感知雷达、自适应信号处理。

E-mail：dailin513＠126.com

崔 琛（1962- ），男，教授，硕士，主要研究方向为雷达信号处理、通信信号处理以及通信系统仿真。

E-mail：dailinincui＠126.com

余 剑（1980- ），男，讲师，硕士，主要研究方向为雷达信号处理、射频信号处理。

E-mail：dailininyu＠126.com

梁 浩（198-7- ），男，博士研究生，主要研究方向为阵列信号处理、MIMO雷达信号处理。

E-mail：lhmailhappy＠163.com

Robust parameter estimation method for CSR based on Bayesian compressed sensing

DAI Lin，CUI Chen，YU Jian，LIANG Hao
（Department of Communication Countermeasure，Institute of Elctronic Engineering，Hefei 230037，China）

In practical application，the mismatch between measurement vector and sensing matrix caused by completely perturbed observations will result in a sharp decline in the performance of parameter estimation for compressed sensing radar（CSR）.A novel robust parameter estimation algorithm is proposed based on Bayesian compressed sensing（BCS）.The completely perturbed sparse linear model is firstly built，and the robust target function is derived with the maximum a posteriori（MAP）of the sparse vector when the completely perturbed matrix obeys Cauchy distribution.Then the optimal solution is achieved through the alternate iteration between the sparse vector and the scale parameter.Compared with most existing recovery algorithm and their derivants，the proposed method effectively improves the robustness against the foregoing mismatch，increases the target detection probability and reduces the estimation error.The effectiveness of the proposed algorithms is demonstrated by computer simulations.

compressed sensing radar（CSR）；completely perturbation；Cauchy distribution；Lorentzian norm；alternate iteration

TN 958.8

A

10.3969／j.issn.1001-506X.2015.11.09

1001-506X（2015）11-2480-07

2014- 11- 24；

2015- 03- 01；网络优先出版日期：2015- 04- 29。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150429.1106.002.html

国家自然科学基金（60702015）资助课题