基于H／α极化分解的弹道目标鉴别

2015-06-05李永祯徐振海王雪松

系统工程与电子技术 2015年11期

关键词：进动诱饵弹头

程旭，李永祯，徐振海，王雪松

（国防科技大学电子科学与工程学院电子信息系统复杂电磁环境效应国家重点实验室，湖南长沙410073）

基于H／α极化分解的弹道目标鉴别

程旭，李永祯，徐振海，王雪松

（国防科技大学电子科学与工程学院电子信息系统复杂电磁环境效应国家重点实验室，湖南长沙410073）

提出了一种基于H／α目标分解理论的弹道目标极化鉴别方法。首先简要给出了H／α目标分解理论的定义和数学模型，然后阐述了真实弹头和诱饵的不同微运动特性，即真弹头具有姿态控制故运动稳定，而诱饵由于没有姿态控制而出现旋转、翻滚等随机运动。在此基础上提取反映目标时间维散射随机性的极化特征量——时间熵。接着利用基于弹头模型暗室测量数据的弹道导弹全极化回波仿真方法，获取了不同战情下弹头与诱饵目标动态特性回波，进而对时间熵进行计算。实验表明，真弹头时间熵值与诱饵熵值可分性明显；时间熵与目标特性有关，但当诱饵与真弹头外形高度逼真时，该特征可有效鉴别真假目标；时间熵亦与所用数据长度（统计窗口）有关，但当统计窗口长度增加到进动周期时，时间熵趋于稳定。

雷达极化；极化分解；H／α分解；微运动

0 引言

当前，极化信息被广泛用于雷达目标检测和分类识别中。特别地，极化目标分解（target decomposition，TD）理论在极化合成孔径雷达（polarimetric synthetic aperture radar，PolSAR）成像、极化逆合成孔径雷达（polarimetric inverse synthetic aperture radar，PolISAR）成像的滤波、目标检测与识别中得到了广泛而深入的研究，并获得了较为成功的应用［13］。在Huynen提出目标分解定理［4］之后，多位学者不断改进和完善，基本形成以下3类目标分解理论：①以Mueller矩阵为基础的分解理论，包括Huynen分解方法［4］和Van Zyl分解方法［5］等；②相干分解，包括Pauli分解、Krogager分解［6］和Cameron分解方法等；③基于相关矩阵或协方差矩阵的本征矢量分解，包括Cloude和Pottier提出的H／α分解［7-8］，Holm等提出的“奇次-偶次漫反射”分解方法［9］等。此外，清华大学的杨健利用目标散射矩阵提出了能够反映目标特征的散射矩阵相似性参数理论［10］。

在这些目标分解技术中，H／α分解由Cloude和Pottier在1997年提出，通过对多次目标散射相干矩阵T进行平均，然后特征分解，提取反映散射混乱程度的散射熵H和平均散射角α。由于这一分解利用多次雷达回波做非相干处理，因此属于非相干分解。它基于“部分极化”目标模型［4］，即由于目标姿态相对雷达视线改变、噪声、干扰等因素而把目标回波看作完全极化与随机极化之和，提取不随目标视线角改变的特征量H和α，相较相干分解而言其假设与实际情形更为契合，因而研究和应用方兴未艾。例如文献［11］提出了极化高分辨一维距离像的H／α分解方法；文献［12］进一步将这种方法用于舰船目标的极化识别；文献［13］对H／α分解方法进行拓展，提出了新的极化特征量伪概率P，利用EMISAR机载SAR系统实测数据验证了H／α／P特征组识别舰船目标的有用性和可靠性。

本文将极化熵用于弹道目标特征提取和识别中，利用真弹头和诱饵的运动特性不同引起的散射随机性差异，提取识别真弹头和诱饵目标的时间熵特征。具体来说，首先介绍经典极化熵的定义，然后通过对弹头和诱饵运动特性不同的阐述表明极化熵特征可用于它们之间的鉴别，籍此提出了一种基于弹道目标全极化雷达回波的时间熵特征提取算法。最后，利用仿真实验验证了时间熵可有效用于弹道目标识别。

1 H／α极化目标分解中的熵特征

全极化雷达同时或轮流发射水平（h）极化信号和垂直（v）极化信号，并同时接收水平、垂直极化回波，一次（对应同时发射）或两次（对应轮流发射）测量可得到完整极化散射矩阵

单站互易情况下有

在Pauli基下对散射矩阵S矢量化，得到散射矢量

进一步得到单次测量的相关矩阵为

假定统计窗口长度内有N次测量，对这N次测量所得相关矩阵取平均有

¯T为半正定Hermit矩阵，对¯T进行特征分解，有

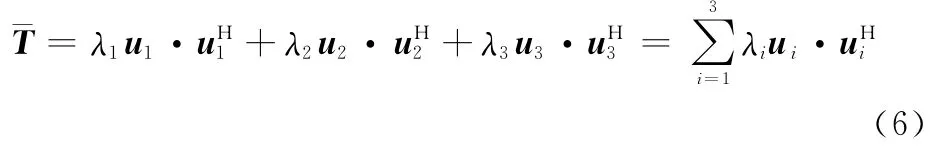
式中，λi为第i个特征值。则散射熵H为

对于式（7），有0≤H≤1。H描述了目标散射的去极化程度。当H比较小时，目标去极化特性较弱，此时可提取目标的主散射机理，即最大特征值对应的特征矢量，而其他两项特征矢量则可忽略不计［7］。已经证明，该特征矢量为主极化散射矩阵的最小二乘估计。特别地，当H＝0时，相关矩阵只有一个特征值不为0，表明目标只具有一种散射机理，此时目标处于完全极化状态；H增大，目标去极化程度增加，目标散射机理类型增加，不再仅存在一个占主要地位的散射机理；在H＝1的极限情况下，所能获得的极化信息为0，目标散射机理完全随机，处于完全非极化状态［12］。通常情况下，该分解方法广泛用于PolSAR图像分解。对大小为M×N的PolSAR图像块，计算其每个距离单元的相关矩阵T（n），再估计M×N区域内的相关矩阵均值〈T（n）〉，从而可进一步求其熵H。

2 基于弹道目标回波提取极化熵

2.1 真假弹头运动特性差异

根据导弹进攻技术，为了提高其命中精度，在弹头的释放过程中，一般会对其采取姿态控制以达到空间定向的目的，其中自旋是最常用的一种空间定向技术［14］。然而在弹头释放过程中不可避免地对弹头产生横向干扰，根据刚体目标姿态动力学知识，弹头在飞行过程中将出现进动［15］。这样除弹体绕自身对称轴的自旋外还将产生绕进动轴的锥弦，而弹体自身对称轴和进动轴的交点即为弹体目标的质心，如图1所示，进动由2个参数（进动频率fm和进动角θm）决定。根据报道，弹头自旋频率为3 Hz左右［14］，进动频率在个位数量级［14，16-17］，即1～10 Hz。而进动角未发现文献明确标明取值范围，一般在5°～15°间取值［14，16-17］。

图1 弹头目标进动示意图

相较而言，诱饵、碎片一般没有姿态控制机制，因此会出现旋转、翻滚的运动方式［14-15］，旋转、翻滚运动可以看作是随机运动［14-18］。图2为美国林肯实验室期刊公布的一幅典型弹道导弹飞行图［13］，可以看出由于存在是否采用姿态控制的差异，弹头和诱饵在中段的运动方式有显著区别。而诱饵在空间姿态的随意翻滚致使其散射随机性也越强，故若能提取反映这种微动特性差异的特征量将有利于真、假弹头的识别。

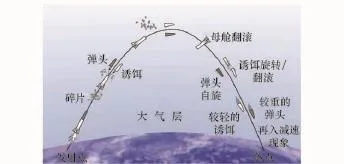
图2 典型弹道导弹飞行过程

2.2 弹道目标极化熵提取

PolSAR中使用的极化熵旨在利用目标的空间几何结构散射随机性。目标越复杂，去极化程度越高，熵值H越大，反之越小。对于处于高速飞行的弹道目标来说，可供防御系统进行识别的时间十分有限，因此提取能够较好反映目标结构特性和运动特征且性能稳健的特征量对于防御方来说具有重要意义。而如第2.1节所述，经过姿态控制的真弹头的运动比仿弹头诱饵更稳定。这里，将极化熵理论引入到弹道目标特征提取和鉴别中，定义一种新的极化熵提取方式——时间熵，即利用雷达目标一段时间内的窄带极化散射矩阵序列估计相关矩阵，进而进行特征分解，求得散射熵值。具体方法为：首先，令T时间内雷达测得N个极化散射序列

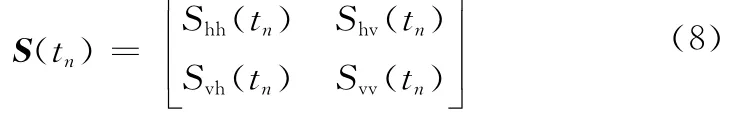
式中，tn＝t0＋nΔt，n＝0，1，…，N－1，Δt为雷达的数据周期。单站互易情况下tn时刻的Pauli变换为

则tn时刻的相关矩阵

进而整个序列的估计为

进一步对T进行特征值分解，有

那么，散射熵H为

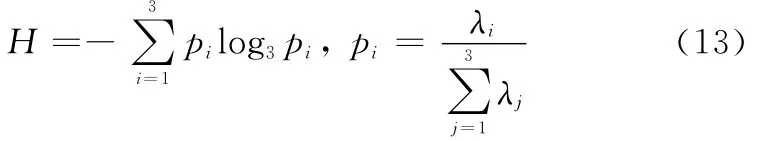
至此完成时间熵提取过程。可见，不同于PolSAR中“熵”的含义，时间熵反映目标的运动随机性。如果目标在一段时间内的运动状态比较稳定，那么其极化散射矩阵的相关性就越强，时间熵H的值越小。反之，当目标的运动趋于随机，姿态变化比较剧烈，那么在这段时间的极化散射矩阵的相关性就越差，时间熵H的值就越大。

3 实验分析

第2节提出了提取时间熵用于真假弹头的鉴别，然而特征是否有效有待检验，故本节将对该特征有效性进行实验验证。首先给出完整实验流程，如图3所示，包括实验数据的生成、时间熵提取和结果分析3个环节。在实验数据生成阶段主要介绍数据生成方法、流程及雷达参数设置，然后利用实验数据初步验证时间熵对弹头和诱饵鉴别的有效性，接着在结果分析环节详细考察不同进动周期和进动角差异条件下时间熵的变化规律，并对影响时间熵测量精度的一些因素展开讨论。需要指出的是，由于弹头外形通常为旋转对称体，自旋并不引起目标电磁散射特性的改变，故在本文的分析中不考虑自旋对时间熵的影响。

图3 算法和处理流程

3.1 弹道目标全极化雷达回波数据仿真

由于导弹的外场飞行实验存在成本高、可重复性差、不可控性大的缺点，同时由于保密方面的要求，开展次数有限且难以将数据广泛用于研究。为此，在本文方法的验证环节，采用文献［19］提出的一种基于暗室测量目标特性数据的空间进动目标动态全极化回波仿真方法，产生弹道目标雷达全极化回波。在图3的目标动态全极化回波数据生成环节已较为详细地给出数据生成所需参数及流程，具体描述如下：

步骤1根据发射点、落点位置参数和初速度计算弹道导弹飞行弹道；

步骤2根据雷达位置参数和目标微运动参数（包括进动周期和进动角）计算目标的姿态序列；

步骤3在目标运动的姿态序列计算完成后，采用插值的方法对弹头模型（见图4）的暗室测量数据进行插值，得到目标的全极化动态回波序列。

图4 弹头暗室测量模型

另暗室测量弹头模型的测量姿态角为：俯仰角0°，横滚角0°，方位角范围为0°～180°，步进间隔为0.2°。发射波形参数为：中心频率f0＝9.75 GHz，带宽Bw＝5 MHz，脉冲重复频率PRF＝100 Hz。发射点地理坐标为北纬24.60°，东经152.46°。落点坐标为：北纬24.32°，东经176.41°。雷达布置在北纬24.06°，东经170.01°。

3.2 实验结果及分析

本节将首先给出真弹头设置具体进动频率和进动角，而诱饵相对雷达姿态角随机改变，初步验证时间熵对弹头和诱饵鉴别的有效性。在此基础上对一系列影响时间熵值的因素进行讨论。

3.2.1 真弹头和诱饵时间熵差异

为验证时间熵对真弹头、诱饵的鉴别结果，利用第3.1节仿真方法，其中暗室测量目标选用圆锥体（如图4（a）所示），弹头的进动频率设fm＝2 Hz，进动角θm＝10°，诱饵相对雷达姿态角设为随机变化，分别计算得到弹头和诱饵的全极化雷达回波，并进一步计算时间熵。计算时间熵时采用滑动窗口方式，即每次利用时长为Ts的采样数据，然后舍弃其前Tt时间内的样本，再引入新的Tt时间数据。这里取统计窗口Ts＝1 s，滑动窗口Tt＝0.1 s。

图5给出弹道中段真弹头和诱饵的时间熵计算结果。可以看出，采用姿态控制的弹头的时间熵始终小于姿态随机变化的诱饵的时间熵，二者具有明显的可分性：其中真弹头的熵值为0.2左右，而诱饵在0.8附近波动。上述结果初步验证了本文所提方法对于鉴别真假弹头是有效的。

为深入研究，本节进一步考察微动参数（包括进动频率和进动角）对时间熵的影响，并对可能影响时间熵精度的其他因素（包括目标特性差异、统计窗口长度等）进行分析并讨论。

图5 真弹头和诱饵时间熵随时间变化曲线

3.2.2 进动参数与时间熵的关系

本节考察进动频率和进动角对时间熵的影响。相对第3.1节的仿真参数设置，仅改变进动参数，其他条件不变，图6给出不同进动参数下真弹头时间熵随时间变化的统计结果，其中图6（a）～图6（d）分别表示进动频率为1 Hz、2 Hz、4 Hz、8 Hz条件下不同进动角时间熵随时间的变化曲线。

根据图中结果可得到以下结论：

（1）在进动频率一定的条件下，进动角越大，时间熵值越高；但在进动频率取值较大时，进动角的明显变化引起时间熵的改变减小，如图6（d）中进动角10°和15°条件下时间熵差异较小。

（2）进动频率越高，时间熵越大。进动频率每次提高都引起图中时间熵的整体抬升。

为进一步清晰显示进动频率与时间熵的关系，给出一组进动角固定、进动频率改变，时间熵的变化情形如图7所示。由图7可明显看出进动频率越高时间熵越大。

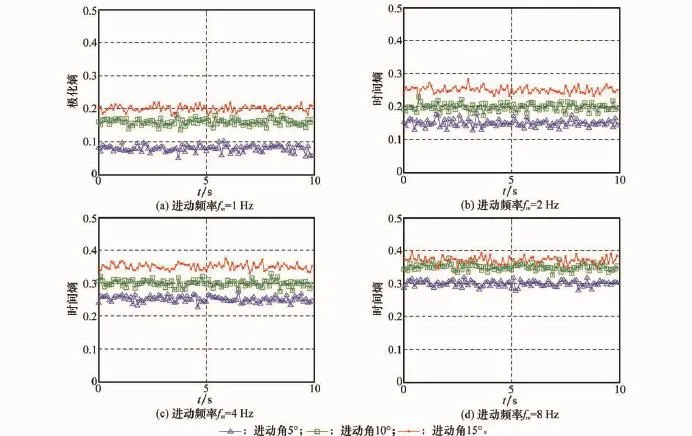
图6 真弹头时间熵随时间变化曲线

图7 进动角10°，不同进动频率下真弹头时间熵随时间变化曲线

然而即使有上述结论，一定范围进动参数取值下的时间熵较姿态随机改变的诱饵的时间熵明显偏低，目标和诱饵可分性明显。

3.2.3 目标体与时间熵的关系

由于“熵”反映的是事物的混乱程度，故时间熵亦和目标本身的结构、尺寸相关。这里进一步考察不同目标特性对时间熵值的影响。利用仿真平台设置不同弹头模型的暗室，测量数据生成不同目标体的动态全极化雷达回波。弹头模型及尺寸在图4中已列出，分别为圆锥、无缝锥球、无翼弹头和有翼弹头。图8和图9分别给出不同目标特性数据下真弹头、仿弹头诱饵的时间熵随时间变化曲线，其中真弹头的进动参数设置为fm＝2 Hz，θm＝10°。

图8 不同目标特性数据条件下真弹头时间熵随时间变化曲线

图9 不同目标特性数据条件下仿弹头诱饵时间熵随时间变化曲线

由图8可见，时间熵和目标结构有关，时间熵取值：有翼弹头＞无翼弹头＞无缝锥球＞圆锥，表明结构越复杂的目标时间熵越大。进一步地，图9也出现相同的取值规律，但对比图8和图9可以看出，弹头外形变化明显不及微运动引起时间熵值的增加，对目标、诱饵间的可分性影响较小。然而通常情况下，进攻方都试图设计出与真弹头外形高度逼真的诱饵以达到欺骗的目的，此时使用反映目标运动特性的时间熵用于真假弹头鉴别具有较强的针对性。

3.2.4 统计窗口长度与时间熵的关系

最后，考察统计窗口长度对时间熵结果的影响。暗室测量目标选用圆锥体，改变进动参数，其他条件同第3.2.1节中设置，图10（a）～图10（d）分别给出进动频率为1 Hz、2 Hz、4 Hz、8 Hz条件下诱饵、真弹头时间熵均值随统计窗口长度的变化情况。根据图10可知，一定范围内统计窗口长度增加，时间熵增大。然而当统计窗口长度增加到某个位置，时间熵会稳定在一具体值。具体来说，诱饵基本在统计窗口增加到0.2 s后时间熵趋于稳定，而对于真弹头时间熵稳定与否与进动角无关，而与进动频率有关。如图10（a）中3种进动角取值均在统计窗口为1 s处时间熵趋于稳定，而对比图10（a）～图10（d）发现，进动频率改变，所需的统计窗口长度发生变化，其中进动频率为1 Hz时，所需统计窗口为1 s，2 Hz时为0.5 s，4 Hz时为0.3 s，8 Hz时为0.1 s。可见，统计窗口长度大于等于进动频率的倒数，即进动周期时，时间熵不再受统计窗口长度不足的影响，取值趋于稳定。结合进动频率在个位数量级的先验知识，统计窗口应大于等于0.1 s。

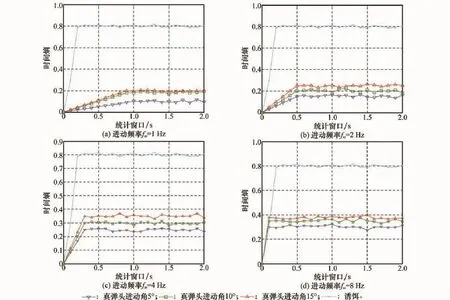
图10 不同统计窗口长度下的时间熵值

最后，对本节实验结果总结如下：当进动参数在经验范围内取值时其时间熵较姿态随机改变的诱饵的时间熵明显偏低，目标和诱饵可分性明显；同时时间熵与目标特性有关，但当诱饵与真弹头高度逼真时，其用于鉴别是有效的；时间熵与采用的数据长度（统计窗口长度）有关系，当统计窗口不足时，其取值偏小，但当统计窗口长度增加到进动周期大小时，时间熵趋于稳定。综合上述结果，时间熵对于鉴别真假弹头是有效的。

4 结论

对于真假弹头识别问题，提出了一种反映真假目标运动特征差异性的极化特征——时间熵，利用仿真实验数据验证了时间熵对鉴别真假弹头的有效性，并对影响时间熵测量准确性及精度的各种因素进行了较为详细的讨论，结果表明，时间熵对于鉴别真假弹头是有效的。

［1］Lee J S，Grunes M R.Unsupervised classification using polarimetric decomposition and the complex wishart classifier［J］.IEEE Trans.on Geoscience and Remote Sensing，1999，37（10）：2249- 2258.

［2］Chen C T，Chen K S，Lee J S.The use of fully polarimetric information for the fuzzy neural classification of SAR images［J］.IEEE Trans.on Geoscience and Remote Sensing，2003，41（5）：2089- 2099.

［3］Riccardo P，Marco M，Fabrizio B.Classification of man-made targets via invariant coherency-matrix eigenvector decomposition of polarimetric SAR／ISAR images［J］.IEEE Trans.on Geoscience and Remote Sensing，2011，49（6）：3022- 3034.

［4］Huynen J R，Mc Nolty F，Hansen E.Component distributions for fluctuating radar targets［J］.IEEE Trans.on Aerospace and Electronic Systems，1975，11（6）：1316- 1332.

［5］Van Z J J.Unsupervised classification of scattering behavior using radarpolarimetry data［J］.IEEE Trans.on Geoscience and Remote Sensing，1989，27（1）：36- 45.

［6］Krogager E.New decomposition of the radar target scattering matrix［J］.Electronics Letters，1990，26（18）：1525- 1527.

［7］Cloude S R，Pottier E.A review of target decomposition theorems in radar polarimetry［J］.IEEE Trans.on Geoscience and Remote Sensing，1996，34（2）：498- 518.

［8］Cloude S R，Pottier E.An entropy based classification scheme for land applications of polarimetric SAR［J］.IEEE Trans.on Geoscience and Remote Sensing，1997，35（1）：68- 78.

［9］Holm W A，Barnes R M.On radar polarization mixed target state decomposition techniques［C］∥Proc.of the Radar Conference，1988：249- 254.

［10］Yang J，Peng Y N，Lin S M.Similarity between two scattering matrices［J］.Electronic Letters，2001，37（3）：193- 194.

［11］Berizzi F，Martorella M，Capria A，et al.H／αpolarimetric features for man-made target classification［C］∥Proc.of the Radar Conference，2008：1- 6.

［12］Guo L，Xiao H T，Zhao H Z，et al.The extraction and optimization of wideband radar target HRRP’s polarization features［J］.Processin Nature Science，2009，19（7）：784- 792.（郭雷，肖怀铁，赵宏钟，等.宽带全极化雷达目标HRRP极化特征提取与优化［J］.自然科学进展，2009，19（7）：784- 792.）

［13］Cuomo K M，Piou J E，Mayhan J T.Ultra-wideband coherent processing［J］.Lincoln Laboratory Journal，1997，10（2）：203- 222.

［14］Zhou W X.BMD radar target recognition technology［M］.Beijing：Publishing House of Electronics Industry，2011.（周万幸.弹道导弹雷达目标识别技术［M］.北京：电子工业出版社，2011.）

［15］Wang T，Wang X，Chang Y，et al.Estimation of precession parameters and generation of ISAR images of ballistic missile targets［J］.IEEE Trans.on Aerospace and Electronic Systems，2010，46（4）：1983- 1995.

［16］Luo H.The simulation and recognition of dynamic target［D］.Beijing：The 2th Research Institute of China Aerospace Science＆Industry Corp，2000.（罗宏.动态雷达目标的建模与识别研究［D］.北京：航天科工集团公司第二研究院，2000.）

［17］Rao B.Study on radar tracking technologies of ballistic targets in the presence of countermeasures［D］.Changsha：National University of Defense Technology，2011.（饶彬.对抗条件下弹道目标的雷达跟踪技术研究［D］.长沙：国防科技大学，2011.）

［18］Ma L.The micro-motion characteristic and combining classification of ballistic target［D］.Changsha：National University of Defense Technology，2011.（马梁.弹道中段目标微动特性及综合识别方法［D］.长沙：国防科技大学，2011.）

［19］Ma L，Li Y Z，Chen Z J，et al.Research on simulation of dynamic full-polarization radar echo for spatial targets［J］.Journal of System Simulation，2012，24（3）：628- 631.（马梁，李永祯，陈志杰，等.空间微动目标动态全极化回波仿真技术研究［J］.系统仿真学报，2012，24（3）：628- 631.）

Ballistic target discrimination based on H／αpolarization decomposition

CHENG Xu，LI Yong-zhen，XU Zhen-hai，WANG Xue-song
（State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System，College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China）

A novel approach for ballistic target discrimination based on H／αpolarization target decomposition is addressed.Firstly，the definition and mathematical model of H／αtarget decomposition are introduced.Then the difference of micro-motion between real warheads and decoys，namely the movement of the warhead is more stable than decoys because of the attitude control，is described.On this basis，the method of extracting the feature，which is called time entropy and related with scattering randomness of ballistic target on the time dimension，is proposed.Then a fully-polarimetric radar echoes simulation procedure based on measurement data of warheads in the anechoic chamber，is intraduced.Thus，the radar echoes of warheads and decoys under different settings are gained so that the time entropy is then calculated.The experimental results show that the difference of the time entropy between the real warhead and decoy is obvious.The value of the time entropy is relevant with the target shape，but for the real warheads and decoys with the similar shape，the feature is valid.The proposed feature is also related with the data length（statistical window），however，when the data length is equivalent to the precession period，the value of the time entropy is stable.

radar polarimetry；polarization decomposition；H／αdecomposition；micro-motion

TN 95

10.3969／j.issn.1001-506X.2015.11.01

程旭（1987 ），男，博士研究生，主要研究方向为极化雷达检测、识别技术。

E-mail：chengxu＠nudt.edu.cn

李永祯（1977 ），男，副研究员，硕士研究生导师，博士，主要研究方向为雷达极化信息处理、空间电子对抗、目标检测与识别。

E-mail：e0061＠sina.com

徐振海（1976 ），男，副教授，硕士研究生导师，博士，主要研究方向为雷达极化阵列信号处理、目标识别技术。

E-mail：tiananle521＠163.com

王雪松（1972 ），男，教授，博士研究生导师，博士，主要研究方向为雷达极化信号处理、信号处理与目标检测及识别、弹道导弹攻防对抗、综合电子战。

E-mail：wxs1019＠vip.sina.com

1001-506X（2015）11-2425-07