外辐射源雷达旋转阵列校正算法

方 亮，龚子平，万显荣，方 高，程 丰

（武汉大学电子信息学院，湖北武汉430072）

外辐射源雷达旋转阵列校正算法

方 亮，龚子平，万显荣，方 高，程 丰

（武汉大学电子信息学院，湖北武汉430072）

外辐射源雷达面临严重的多径干扰，但强多径信号也为阵列校正提供了优良的信号源，针对此提出了一种利用最强径信号的旋转阵列校正算法。该算法首先采用时域相关运算分离出最强径信号，然后通过旋转阵列来增加信号源和提供先验信息，接着利用比幅原理估计出阵列幅度误差，最后结合最大似然（maximum likelihood，ML）算法和最小二乘（least square，LS）算法估计出最强径信号到达角和阵列相位误差。分析了所提算法的适用条件，并推导了最强径信号到达角和阵列相位误差估计的克拉美-罗下界（Cramer-Rao lower bound，CRLB）。仿真和实测数据处理结果验证了该算法的有效性。

外辐射源雷达；阵列校正；最大似然算法；阵列旋转

0 引 言

近年来，外辐射源雷达若干关键技术一直是雷达界的研究热点［1］。国内外学者的研究主要集中在：多径杂波抑制［24］、目标检测［5-7］、目标跟踪［810］、成像［1113］和优化布站［1415］等方面，但少有关于外辐射源雷达阵列校正问题的研究报道。通常采用的辅助信号源的阵列校正方案，包括远场校正和近场校正。其中远场校正将辅助信号源置于天线前方足够远的开阔场地发射校正信号，通过测量各接收通道的输出，扣除阵列空间位置引起的相位差，得到阵列误差信息。不足之处在于：辅助信号源的放置和维护比较麻烦，且难以做到实时校正；此外，当辅助信号源方位信息出现偏差时会给校正带来系统误差。相比之下，近场校正将辅助信号源置于天线阵附近，使得辅助信号源的放置和维护相对容易，且能够实现实时校正，但是天线阵列近场电磁环境复杂，校正信号回波不是理论上的球面波，使得应扣除的空间相位差不能根据简单的几何关系计算，导致该方法的校准精度较差。

为克服辅助信号源的限制，本文结合外辐射源雷达多径干扰严重的特点，提出了利用强多径回波校正阵列的新方法。该方法利用机会照射源信号的强自相关性，采用时域相关运算分离多径，选用最强径信号作为校正信号源，以满足校正信号源高信噪比（signal-to-noise ratio，SNR）的要求。在理想条件下，最强径信号为直达波信号，其到达角可根据收发站的几何关系直接计算出；然而由于实际传播（如单频网配置下城市环境中的多径传播）的复杂性，可能导致直达波被固定建筑物遮挡，使得最强径信号的方位未知。

针对校正信号源方位未知时阵列误差估计的问题，国内外学者提出了多种有效的方法［1618］。文献［16］利用均匀线阵接收信号协方差矩阵的Toeplitz特性求解阵列误差，但求解存在模糊，必须添加相应的限制条件；文献［17］利用噪声子空间与信号子空间的正交性，构造代价函数，通过迭代运算求得校正信号源方位和阵列误差，但对于均匀线阵，该方法的解也存在模糊；文献［18］利用多个在时间或频谱上不重叠的未知方位回波信号，通过最大似然（maximum likelihood，ML）估计阵列误差，但要求阵列为非直线阵。

由于均匀线阵导向矢量的范德蒙特性，以上方法应用于均匀线阵均会导致解存在模糊，然而均匀线阵因其结构和信号处理简单被广泛应用于外辐射源雷达，为解决该阵列的校正，本文提出通过旋转阵列来增加信号源和提供先验信息（即旋转角度），利用比幅原理估计出阵列幅度误差，并结合ML算法和最小二乘（least square，LS）算法估计出最强径信号到达角和阵列相位误差。

本文首先建立了相应的信号模型，接着阐述了所提阵列误差估计算法的原理，分析了其适用条件，推导了最强径信号到达角和阵列相位误差估计的克拉美-罗下界（Cramer-Rao lower bound，CRLB），然后通过仿真和实测数据处理验证了该算法的性能，最后给出了结论。

1 信号模型

本文假定机会照射源为数字电视广播，如中国移动多媒体广播（China mobile multimedia broadcasting，CMMB）［19］、数字电视地面广播（digital television terrestrial broadcasting，DTTB）［20］等，其一般采用正交频分复用（orthogonal frequency division multiplexing，OFDM）调制，不失一般性，经信号重构［21］获得的参考信号可表示为

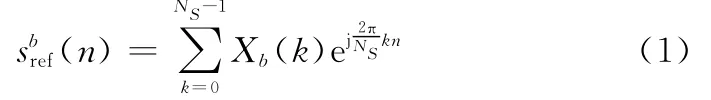
式中，b为OFDM符号序号；k为子载波序号；NS为OFDM符号子载波数；Xb（k）为第b个OFDM符号中第k个子载波调制的经星座映射后的复数据。

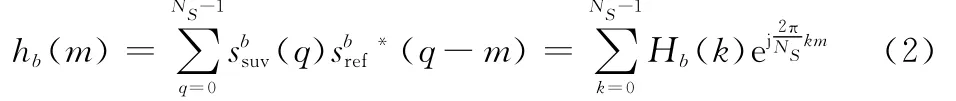
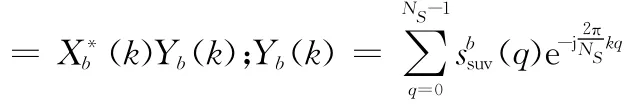
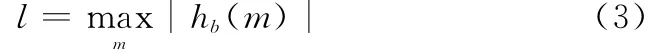
假定接收阵列为均匀线阵，阵元数为M，阵元间距d＝λ／2，其中λ为波长，各阵元为全向天线。本文只考虑阵列幅相误差，不考虑阵列互耦和位置误差，假设幅度误差为gi，相位误差为，其中i＝1，2，…，M为阵元序号，以阵元1为基准，则g1＝1，φ1＝0。如图1所示，将阵列分别顺时针旋转两次，那么阵元i对应于符号b的最强径谱点输出为

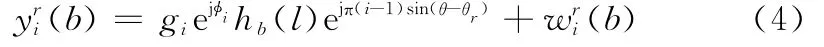
式中，θ为最强径的到达角；θr为旋转角度，其中r＝0，1，2，θ0＝0；（b）为噪声。假设（b）满足：①不同阵元的噪声谱相互独立；②不同时刻的噪声谱相互独立；③不同旋转角度位置的噪声谱相互独立；④噪声为具有相同方差σ2的零均值高斯分布随机变量。

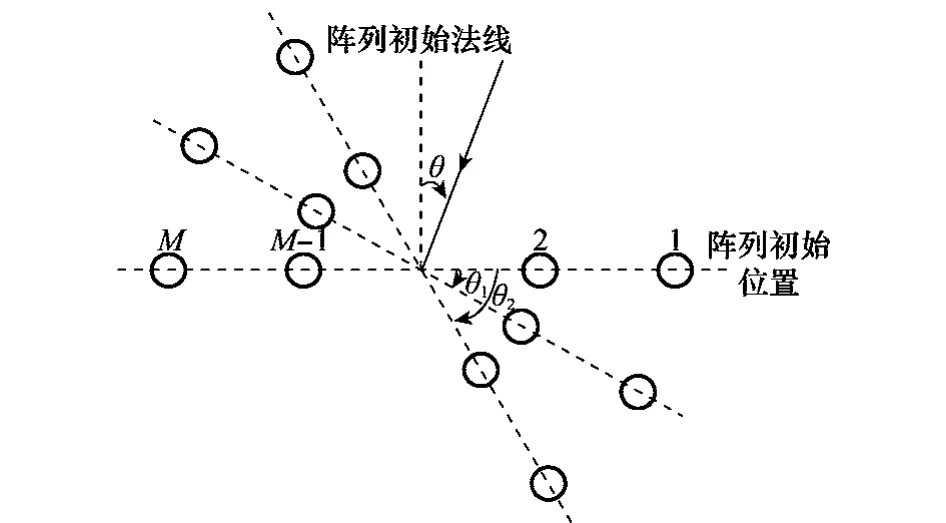
图1 阵列旋转示意图

2 校正算法

2.1 算法原理

2.1.1 阵列幅度误差估计

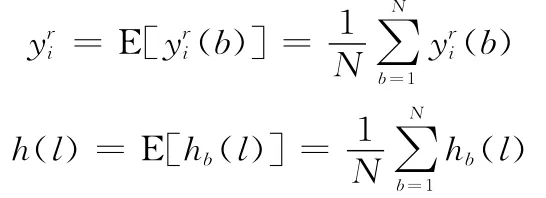
则

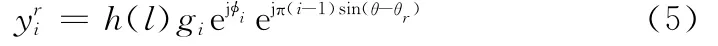
通过共轭相乘抵消相位，则

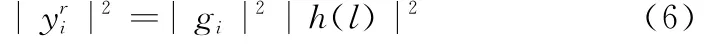
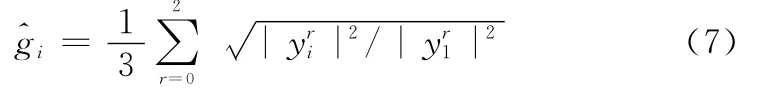
2.1.2 阵列相位误差估计

首先利用求得的阵列幅度误差估计^gi对幅度进行校正，则

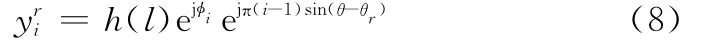
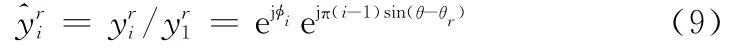
定义阵列相位误差矩阵

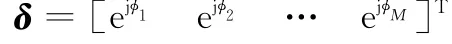
方向向量矩阵

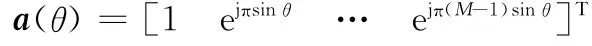
则

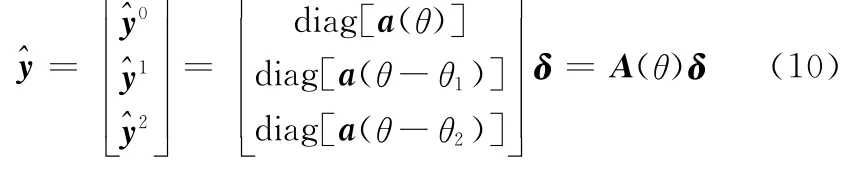
式中

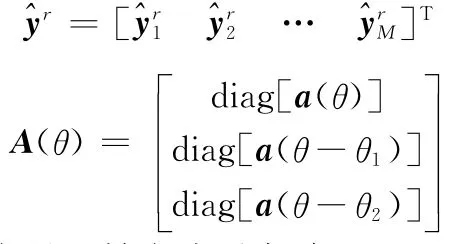
diag［a］表示将向量a转变成对角阵。

假设θ已知的情况下，利用LS算法求解阵列误差矩阵

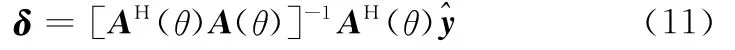
将式（11）代入式（10），则

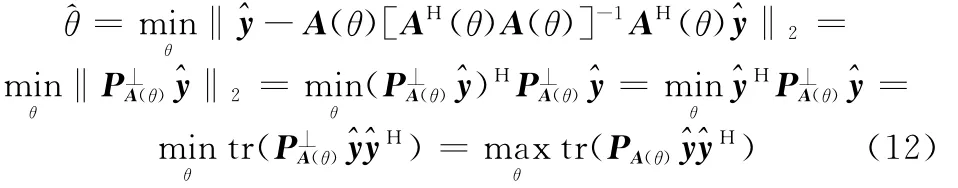
式中

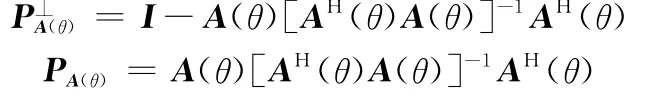
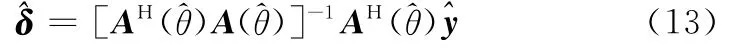
2.2 适用条件

利用AH（θ）A（θ）＝3IM获得的解析表达

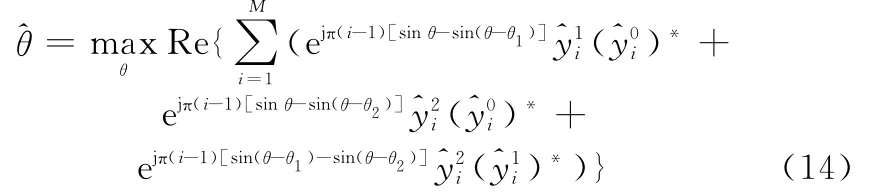
即分别最大化

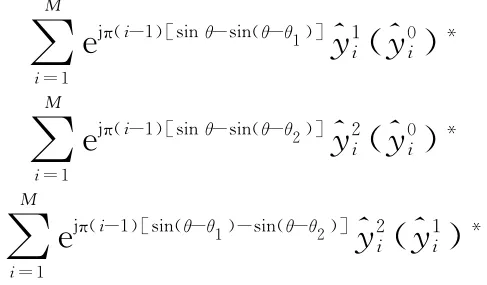
均可通过傅里叶谱分析完成，而同时满足这3个最大化使解存在且唯一。

同理，当阵列只旋转一次时，式（14）变为

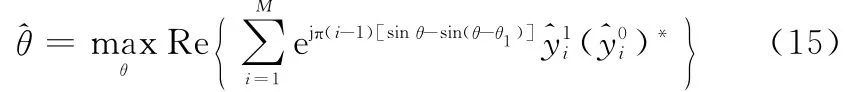
此时该问题会存在两个相等的极大值，导致解存在模糊。为克服该模糊，阵列至少旋转两次。

同理，当利用额外的多径信号源时，式（14）变为

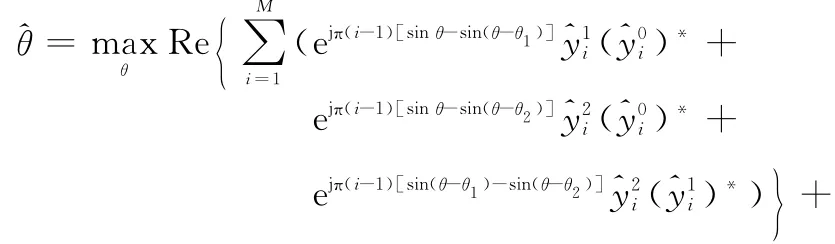
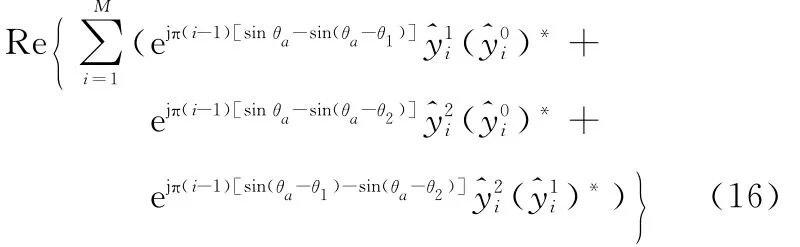
式中，θa为额外的待估计多径信号到达角。可见增加可用的多径信号源不影响该问题的解，所以只需选用最强径信号作为校正源。

2.3 克拉美-罗下界

定义

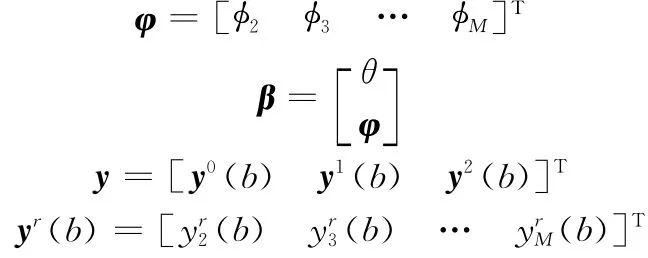
那么相应的似然函数为

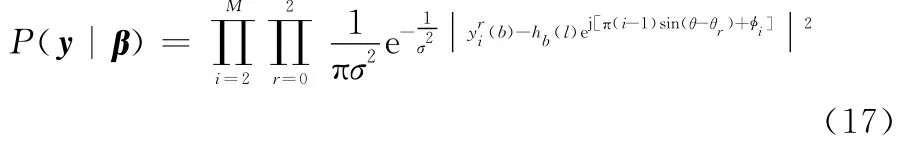
取对数，则

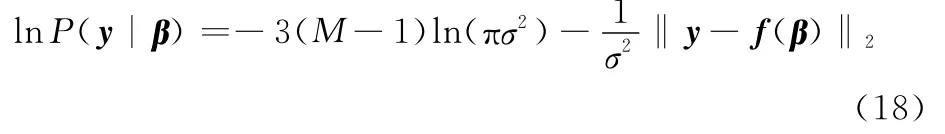
式中

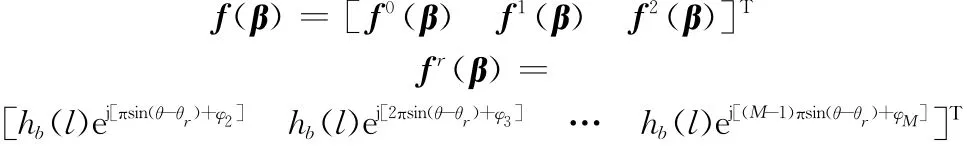
定义矩阵

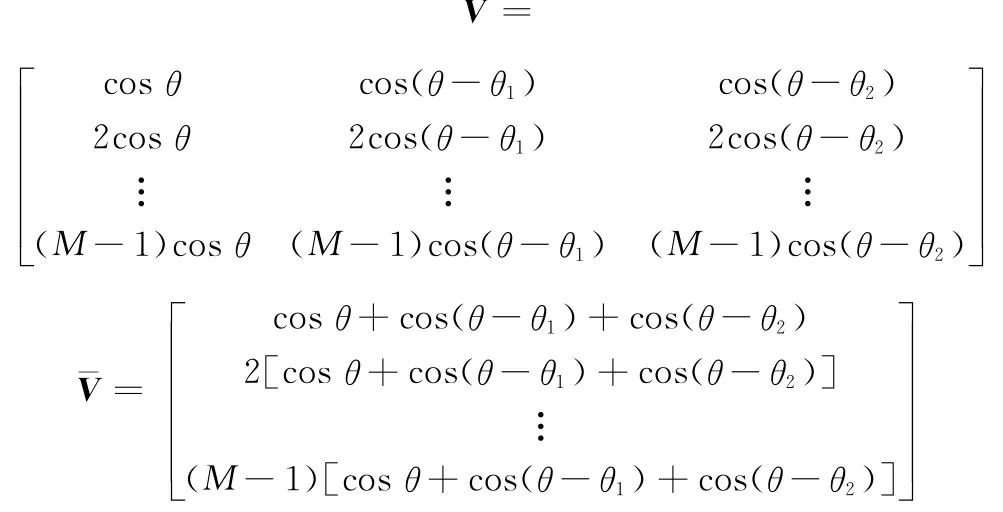
那么Fisher信息矩阵为

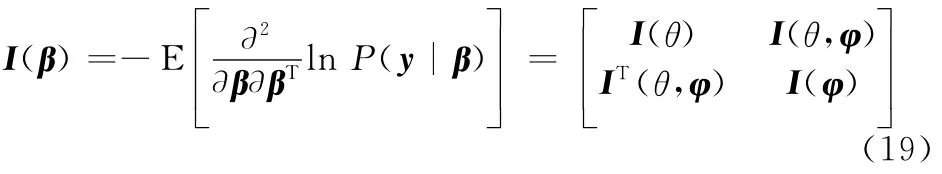
式中

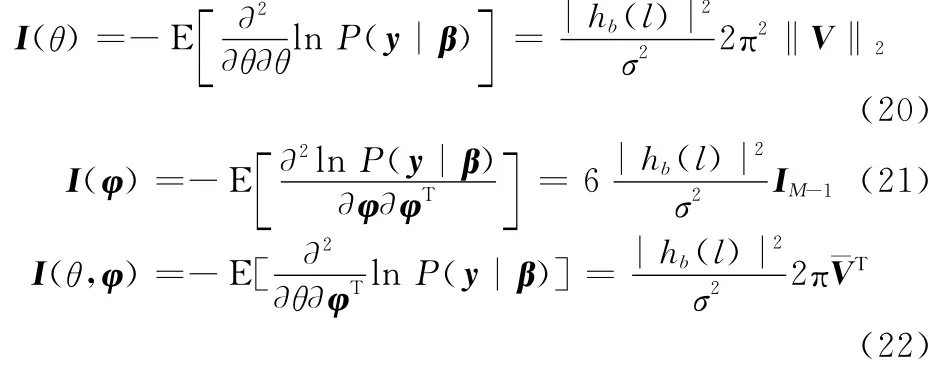
最终得到CRLB，即

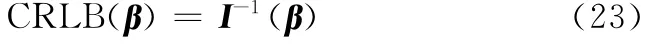
3 性能仿真

为评估算法的性能，本文首先通过计算机数值仿真分别研究了最强径SNR、阵元个数、阵元序号、旋转角度大小、旋转角度误差对阵列幅相误差和最强径到达角估计精度的影响。本仿真基本设置如图1所示，其中机会照射源选用数字电视广播，接收阵列为均匀线阵，阵元数为M，阵元间距d＝λ／2，阵列分别顺时针旋转角度θ1和θ2，最强径信号到达角为θ。

3.1 最强径SNR的影响

实验设置如下：

（1）阵元个数：M＝8；

（3）最强径信号到达角：θ＝5°；

（4）阵列旋转角度：θ1＝10°，θ2＝20°；

（5）蒙特卡罗实验次数：100。

最强径SNR对估计精度的影响如图2所示。从图中可以看出，阵列幅相误差和最强径到达角的估计精度都随着最强径SNR的增加而提高，当最强径SNR达到20 dB时，阵列幅度均方根误差（root mean square error，RMSE）降到10－4，阵列相位RMSE低于1°，最强径到达角RMSE低于0.05°，此时RMSE非常接近CRLB。在实际场景中，最强径SNR一般高于20 dB，可使阵列幅相误差估计达到较高的精度。

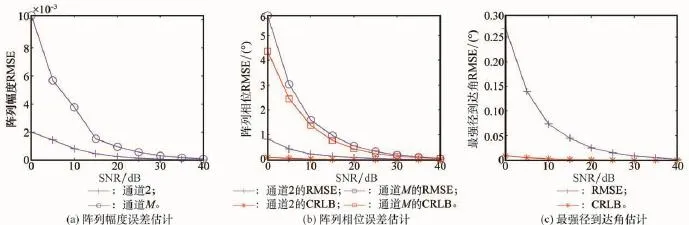
图2 最强径SNR对估计精度的影响

3.2 阵元个数的影响

实验设置如下：

（2）最强径信号到达角：θ＝5°；

（3）阵列旋转角度：θ1＝10°，θ2＝20°；

（4）最强径SNR＝10 d B；

（5）蒙特卡罗实验次数：100。

阵元个数对估计精度的影响如图3所示。从图中可以看出，阵元个数对阵列幅度误差估计精度基本没有影响，对阵列相位误差和最强径到达角估计精度影响很小。这表明，在实际场景中，利用较少的阵元个数也可达到较高的阵列幅相误差估计精度。

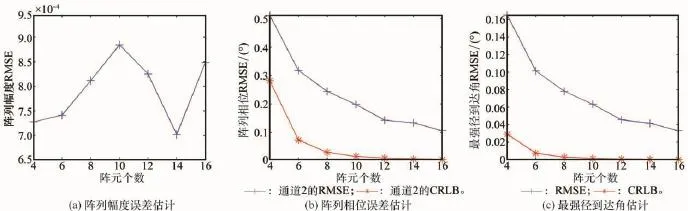
图3 阵元个数对估计精度的影响

3.3 阵元序号的影响

实验设置如下：

（1）阵元个数M＝8；

（3）最强径信号到达角：θ＝5°；

（4）阵列旋转角度：θ1＝10°，θ2＝20°；

（5）最强径SNR＝10 dB；

（6）蒙特卡罗实验次数：100。

阵元序号对估计精度的影响如图4所示。从图中可以看出，随着阵元与阵元1（基准阵元）距离增加，阵列幅相误差估计精度会有所下降。

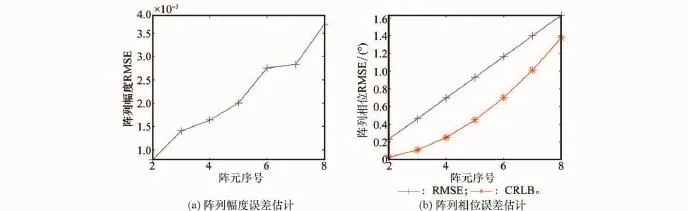
图4 阵元序号对估计精度的影响

3.4 旋转角度大小的影响

实验设置如下：

（1）阵元个数M＝8；

（3）最强径信号到达角：θ＝5°；

（4）阵列旋转角度：θ2＝2θ1；

（5）最强径SNR＝10 dB；

（6）蒙特卡罗实验次数：100。

旋转角度大小对估计精度的影响如图5所示。从图中可以看出，旋转角度大小对阵列幅度误差估计精度几乎没有影响，对阵列相位误差和最强径到达角估计误差影响很小，总的趋势是，随着旋转角度增大，估计精度会有所提高。在实际场景中，旋转较小的角度也可实现较高的阵列相位误差估计精度，利于工程实现。

图5 旋转角度大小对估计精度的影响

3.5 旋转角度误差的影响

实验设置如下：

（1）阵元个数M＝8；

（3）最强径信号到达角：θ＝5°；

（4）阵列旋转角度：θ1＝（10＋δθ）°，θ2＝（20＋δθ）°；

（5）最强径SNR＝10 dB；

（6）蒙特卡罗实验次数：100。

旋转角度误差对估计精度影响如图6所示。从图中可以看出，旋转角度误差对阵列幅度误差估计精度基本没有影响，但对阵列相位误差和最强径到达角估计精度有较大的影响，为保证估计精度，旋转角度误差应控制在0.1°以内。在实际场景中，可通过高精度的转盘实现阵列旋转。

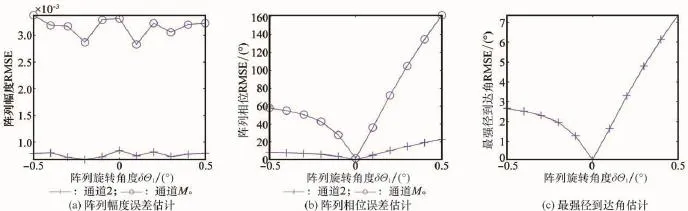
图6 旋转角度误差对估计精度的影响

4 实测数据处理

近年来，武汉大学研制出了基于数字电视广播信号的外辐射源雷达系统。利用该系统实测数据来验证所提算法，其中阵列布置如图1所示，阵列为均匀线阵，阵元数为8，阵元间距为0.2 m，阵列置于转盘上，顺时针旋转两次，其旋转角度分别为10°和20°。同时，本文结合辅助信号源来校正阵列，以比对校正值。实测数据处理结果如图7所示。其中图7（a）和图7（b）比对了旋转阵列校正和辅助信源校正的幅相校正值，可见两种方法的幅相校正值基本一致，表明本文所提算法是有效的。图7（c）为最强径校正前后的多重信号分类（multiple signal classification，MUSIC）谱，校正前最强径谱峰不明显，经本文算法校正后其谱峰明显突出且尖锐，再次验证了其有效性。

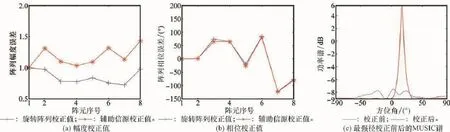
图7 实测数据处理结果

5 结 论

本文提出了一种外辐射源雷达阵列校正算法，该算法利用最强径信号作为校正源，通过旋转阵列克服了线阵的解模糊；而且其运算量小，只需要参数的一维搜索，不存在参数联合估计的局部收敛问题。与辅助信号源的校正方法相比，本文方法摆脱了辅助信号源的限制，只需旋转两次阵列，简单易行。需要说明的是，虽然本文重点以数字电视广播外辐射源雷达为例来验证所提算法的有效性，但所提算法同样适用于其他体制外辐射源雷达。

［1］Wan X R.An overview on development of passive radar based on the low frequency band digital broadcasting and TV signals［J］.Journal of Radars，2012，1（2）：109- 123.（万显荣.基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势［J］.雷达学报，2012，1（2）：109- 123.）

［2］Demissie B.Clutter cancellation in passive radar using GSM broadcast channels［J］.IET Radar，Sonar and Navigation，2014，8（7）：787- 796.

［3］Tan D K P，Lesturgie M，Sun H B，et al.Space-time interference analysis and suppression for airborne passive radar using transmissions of opportunity［J］.IET Radar，Sonar and Navigation，2014，8（2）：142- 152.

［4］Wang H T，Wang J，Liu Y C.Interference suppression for GSM based PBR using two-step spatial filtering［J］.Systems Engineering and Electronics，2013，35（4）：740- 744.（王海涛，王俊，刘玉春.基于两步空域滤波的GSM辐射源雷达干扰抑制［J］.系统工程与电子技术，2013，35（4）：740- 744.）

［5］Howard S D，Sirianunpiboon S.Passive radar detection using multiple transmitters［C］∥Proc.of the Asilomar Conference on Signals，Systems and Computers，2013：945- 948.

［6］Malanowski M.Detection and parameter estimation of manoeuvring targets with passive bistatic radar［J］.IET Radar，Sonar and Navigation，2012，6（8）：739- 745.

［7］Wang H T，Wang J，Duan F.Target detection for CDMA based passive radar using array antenna［J］.Systems Engineering and Electronics，2012，34（2）：282- 286.（王海涛，王俊，端峰.利用阵列天线的CDMA辐射源雷达目标检测方法［J］.系统工程与电子技术，2012，34（2）：282- 286.）

［8］Choi S，Crouse D F，Willett P，et al.Approaches to Cartesian data association passive radar tracking in a DAB／DVB network［J］.IEEE Trans.on Aerospace and Electronic Systems，2014，50（1）：649- 663.

［9］Brotje M，Nickel U.Data ambiguity in passive radar tracking［C］∥Proc.of the International Radar Symposium，2013：349- 354.

［10］Klein M，Millet N.Multireceiver passive radar tracking［J］.IEEE Trans.on Aerospace and Electronic Systems，2012，27（10）：26- 36.

［11］Garry J L，Baker C J，Smith G E，et al.Investigations toward multistatic passive radar imaging［C］∥Proc.of the IEEE Radar Conference，2014：607- 612.

［12］Antoniou M，Zhou H，Zeng Z F，et al.Passive bistatic synthetic aperture radar imaging with Galileo transmitters and a moving receiver：experimental demonstration［J］.IET Radar，Sonar and Navigation，2013，7（9）：985- 993.

［13］Wang S，Tang Y H，Liu C C，et al.Sparse passive radar imaging based on FM station using the U-ESPRIT for moving target［C］∥Proc.of the IET International Radar Conference，2013：1- 6.

［14］Gumiero F，Santarelli S，Bongioanni C，et al.Using real data for the implementation of multistatic passive radar geometry optimization procedure［C］∥Proc.of the European Radar Conference，2011：93- 96.

［15］Isohookana M，Pyykonen J.Design of a passive radar network［C］∥Proc.of the European Radar Conference，2010：443- 446.

［16］Wylie M P，Roy S，Messer H.Joint DOA estimation and phase calibration of linear equispaced（LES）arrays［J］.IEEE Trans. on Signal Processing，1994，42（12）：3449- 3459.

［17］Weiss A J，Friedlander B.Eigenstructure methods for direction finding with sensor gain and phase uncertainties［J］.Circuits Systems Signal Process，1990，9（3）：271- 300.

［18］Rockah Y，Messer H，Schultheiss P M.Localization performance of arrays subject to phase errors［J］.IEEE Trans.on Aerospace and Electronic Systems，1988，24（4）：402- 410.

［19］GY／T 220.1- 2006.Mobile multimedia broadcasting part 1：framing structure，channel coding and modulation for broadcasting channel［S］.China mobile multimedia broadcasting standard，2006.（GY／T 220.1- 2006.移动多媒体广播第l部分：广播信道帧结构、信道编码和调制［S］.中国移动多媒体标准，2006.）

［20］GB 20600- 2006.Framing structure，channel coding and modulation for digital television terrestrial broadcasting system［S］.Chinese National Standard，2006.（GB 20600- 2006.数字电视地面广播传输系统帧结构，信道编码和调制［S］.中国国家标准，2006.）

［21］Baczyk M K，Malanowski M.Reconstruction of reference signal in DVB-T-based passive radar［J］.International Journal of Electronics and Telecommunications，2011，57（1）：43- 48.

方 亮（198-6- ），男，博士研究生，主要研究方向为雷达系统与信号处理。

E-mail：fangliang198612＠126.com

龚子平（197-7- ），男，讲师，博士，主要研究方向为电波传播与无线电海洋遥感。

E-mail：zpgong＠whu.edu.cn

万显荣（197-5- ），男，教授，博士研究生导师，博士，主要研究方向为新体制雷达系统设计、阵列信号处理。

E-mail：xrwan＠whu.edu.cn

方 高（198-9- ），男，博士研究生，主要研究方向为雷达系统与信号处理。

E-mail：fanggao55＠whu.edu.cn

程 丰（197-2- ），男，副教授，硕士研究生导师，博士，主要研究方向为雷达信号处理、目标检测与跟踪。

E-mail：ryh＠whu.edu.cn

Calibration algorithm using array rotation in passive radar

FANG Liang，GONG Zi-ping，WAN Xian-rong，FANG Gao，CHENG Feng
（School of Electronic Information，Wuhan University，Wuhan 430072，China）

Passive radar usually encounters aggravated multipath interferences，which nonetheless provide effective signal sources for array calibration.A novel approach for array calibration in passive radar is proposed，exploiting the strongest multipath signal and array rotation.Firstly，the time-domain correlation between the surveillance and reference signals is employed to extract the strongest multipath signal.And then，the array rotation which provides both additional calibration sources and priori knowledge about the rotating angle is utilized.Following that，the estimation of the array amplitude mismatch by comparison on amplitudes，the direction of arrival（DOA）of the strongest multipath signal and the array phase mismatch are finally estimated using the incorporation of maximum likelihood（ML）and least square（LS）algorithms.The applicable condition of the proposed approach is investigated，and the Cramer-Rao lower bound（CRLB）for DOA of the strongest multipath signal and the array phase mismatch is also derived.Numerical simulation and field data results demonstrate the behavior and effectiveness of the proposed algorithm.

passive radar；array calibration；maximum likelihood（ML）algorithm；array rotation

TN 958.97

A

10.3969／j.issn.1001-506X.2015.11.07

1001-506X（2015）11-2467-07

2014- 12- 11；

2015- 01- 27；网络优先出版日期：2015- 03- 30。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150330.0851.007.html

国家自然科学基金（61331012，61371197）；国家基金委和民航总局联合基金（U1333106，）；教育部博士点基金（博导类）（20120141110077）资助课题