基于空间域划分的分布式SLAM算法

2015-06-05裴福俊程雨航李昊洋居鹤华

系统工程与电子技术 2015年3期

关键词：集中式标点位姿

裴福俊,程雨航,李昊洋,居鹤华

(1.北京工业大学电子信息与控制工程学院,北京100124; 2.计算智能与智能系统北京市重点实验室,北京100124)

基于空间域划分的分布式SLAM算法

裴福俊1,2,程雨航1,2,李昊洋1,2,居鹤华1,2

(1.北京工业大学电子信息与控制工程学院,北京100124; 2.计算智能与智能系统北京市重点实验室,北京100124)

针对同步定位与地图构建(simultaneous localization and mapping,SLAM)中状态量高维时变的问题,本文通过综合集中式和分布式实现结构的各自优势,提出了一种基于空间域划分的分布式SLAM算法。该算法依据两个路标点与机器人连线之间的夹角,将整个空间域中的路标点进行区域划分,保证每个子空间域内含有两个不共线的路标点,并将每个空间域内的路标点组合构建观测模型,采用分布式无味粒子滤波器进行机器人位姿的估计,而采用联邦Kalman滤波完成对路标点的估计,并通过设计各子滤波器中粒子分布的调整方式改善了系统在动态重构过程的精度和稳定性。最后,通过实际数据的仿真试验证明所提算法具有更好的实时性和滤波精度。

同步定位与地图构建;空间域划分;分布式结构;动态重构

0 引言

同步定位与地图构建(simultaneous localization and mapping,SLAM)已经被世界上很多学者认为是实现移动机器人自主移动的关键技术[13],也成为了移动机器人相关研究的核心和难点。SLAM实际是一个非线性非高斯的状态估计问题,国内外学者采用了多种非线性最优估计方法来解决SLAM问题,例如扩展卡尔曼滤波(extended Kalman filer,EKF)[4]、无迹卡尔曼滤波(unscented Kalman filer,UKF)[5]、粒子滤波(particle filter,PF)[6]等。由于粒子滤波在解决非线性非高斯状态估计问题方面的优越性,成为了近年来国内外学者研究的热点方向,但其繁重的计算量制约了PF-SLAM的实时应用。针对PF-SLAM存在的问题,文献[7]提出了RBPF-SLAM系列算法,随后又对其进行了扩展提出了Fast-SLAM1.0算法,将SLAM问题的过程模型直接作用于采样粒子的重要性函数,之后文献[8]提出了改进的Fast-SLAM2.0算法,提高了Fast-SLAM算法的精度。但是,这些算法均采用了集中式滤波器结构,即用一个滤波器完成对位姿与环境地图的同时估计,这种结构中的状态向量均是包括机器人和路标信息的高维向量,并且状态向量维数将随环境动态时变,必然造成集中式SLAM算法存在计算量大、稳定性和容错性差等问题。

与集中式SLAM算法相对应的是基于分布式结构的SLAM算法,文献[9]首先提出了一种基于分布式结构的SLAM算法,将整个状态向量分为机器人位姿估计和路标估计两个过程,依据每个有效路标点单独建立子滤波器,分别实现对机器人位姿和路标的估计。在分布式滤波结构中,处理多维向量的集中滤波器被拆分成处理单个向量组成的子滤波器形式,从而有效降低了SLAM算法的计算复杂度,并提高了容错能力,但也造成了诸如各个子滤波器之间的信息融合精度差、子滤波器重构致使系统稳定性无法得到保证以及单个子滤波器中的粒子退化等问题。文献[10-11]在文献[9]的基础上,针对分布式粒子滤波SLAM算法进行了改进,并对分布式粒子滤波的收敛性进行了证明。

结合集中式和分布式两种结构模型的优点,本文提出了一种基于空间域划分的分布式SLAM算法。该算法针对机器人自带传感器所探测的整个环境空间,依据两个路标点与机器人连线之间的夹角为大值的条件,将整个空间域中的路标点进行区域划分,保证每个子空间域内含有两个不共线的路标点,并将每个空间域内的有效路标点组合构建子滤波器的观测模型,该算法保持了分布式结构的计算量小、容错性好的优点,同时提高了各个子滤波器的估计精度。针对所建模型的非线性特点,本文采用了分布式无迹粒子滤波(unscented particle filter,UPF)进行机器人位姿的估计,并采用联邦卡尔曼滤波(federated Kalman filter,FKF)完成对路标点的估计。同时,充分利用UPF对于粒子分布的调整作用,利用空间域内没有经历动态重构的路标点进行量测更新有效地改善粒子分布,提高了系统的稳定性和鲁棒性。

1 SLAM模型

1.1 过程模型

SLAM系统状态模型可看作一个马尔可夫过程,即t时刻状态与t-1时刻前的状态无关。系统中机器人的运动控制信息由里程计提供,如图1所示,为机器人的状态转移过程及实际机器人坐标系。

图1 机器人状态转移过程及坐标系定义

运动过程中机器人的状态[10]可以描述如下:st=(x,y, θ)T,其中,x,y表示坐标值,θ表示偏航角(θ=0表示指向x轴正向,θ=π/2表示指向y轴正向)。机器人的状态转移模型如下:

式中,XL(t)=(xL(t)yL(t)ϕL(t))T为机器人在t时刻的位姿;ΔT为时间变化量;vc为机器人移动速度;α为机器人变化的角度;L为两轮轴间距;γ为高斯白噪声。

1.2 量测模型

本文是依据激光传感器给出机器人的观测模型,测距激光传感器的观测量z是某个环境特征相对于传感器的距离以及角度,在扫描目标时容易出现误差,实际状况中,误差密度函数由各种分布组合而成,一般情况包括:指数分布、均匀分布、高斯分布等,本文采用高斯分布描述误差的分布情况。

将机器人状态信息与观测信息相关联,可以获得路标点的观测模型[10]:

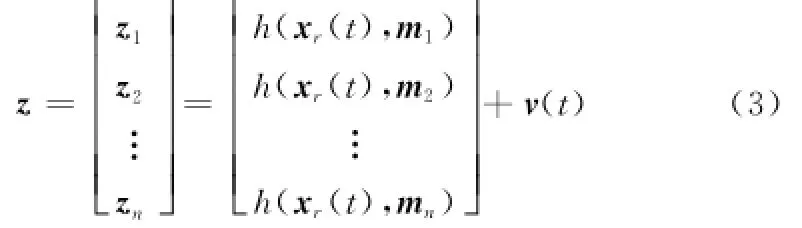
而在分布式模型中,则模型改写为如下形式:

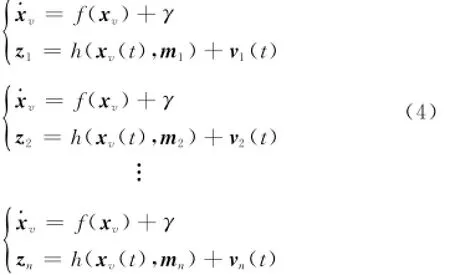
2 集中式与分布式SLAM算法对比分析

从式(2)和式(3)可以看出,SLAM问题是非线性非高斯的状态估计问题。集中式SLAM算法是采用了单一滤波器实现对机器人位姿和路标点的估计[12],不可避免地存在计算量大、复杂度高、容错性差、实时性差的问题。而分布式SLAM算法是将本应以矩阵形式集中计算的描述机器人位姿的粒子分布概率公式进行分布化处理,之后在子滤波器中处理概率计算,最后根据相应的融合算法进行主滤波器融合[13]。这样大大减少了计算复杂度,提高系统容错能力,针对集中式和分布式中的核心算法的对比分析如下:

首先,从粒子表征的角度来说,对于集中式SLAM算法,滤波器输出结果即是用以表征机器人位置信息的粒子分布,如式(5)中左式所示;而分布式SLAM算法中,则每个子滤波器中均有对机器人位置的估计如式(5)中右式所示。

其次,集中式SLAM滤波器中的状态维数随着路标点个数M时变,根据控制信息ut得到粒子预测分布后,将量测信息融入构成N个粒子的权重值,M个路标点的权值计算过程如式(6)所示,其中粒子标号i=1,2,…,N,路标点标号j=1,2,…,M。

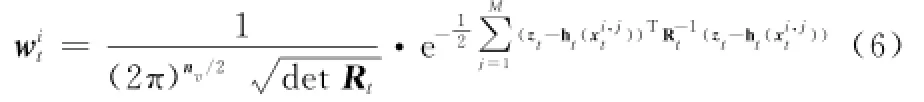
根据权重值更新,可输出位姿估计的计算结果如式(7)。

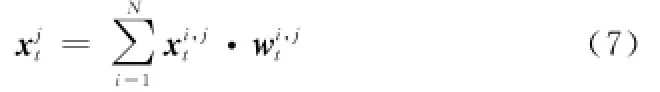
而分布式SLAM中各滤波器所处理的数据维数固定且为总维数的1/M,根据各子滤波器中粒子群的预测分布,然后对每个子滤波器中的粒子进行重要性权值估计如式(8)所示。

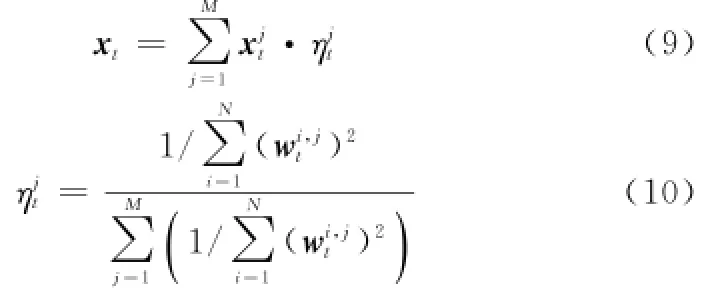
根据子滤波器位姿结果,进行主滤波器的融合。如式(9)及式(10)所示。最后,集中式SLAM算法中,最终位姿的概率分布可表示为式(11),并将带有wit权值的样本映射为等权样本。设置阈值Nthreshold,当有效粒子数时,进入重采样过程。

而分布式SLAM中,最终位姿是主滤波器进行数据融合的结果,其概率分布可表示为式(12)的形式,各子滤波器独立进行重采样:,为保持粒子集一致性,需要定期全局重采样。

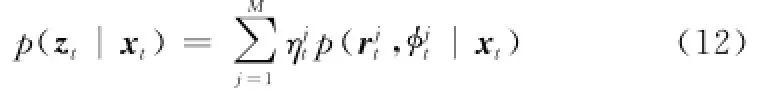
通过对两者的比较,对于两者的算法流程对估计结果的影响,分析如下:

式(11)和式(12)反映了集中式与分布式两种方式的概率分布求解的不同之处:集中式粒子滤波器在每个单步的估计精度更高,可以更好地降低估计的不确定性,但是不可避免地会受到多维向量不断增加和重构造成的影响,造成算法的稳定性、容错性和计算量问题。而分布式结构可以有效降低计算的复杂度和计算量,但由于每个子滤波器只考虑相对应的路标点,需要按照式(10)进行子滤波器的融合,导致融合算法中的ηjt直接决定了融合输出的结果,而ηjt与有效粒子数有关,也就与式(9)中每个子滤波器中权值的估计结果相关,从而由于单个子滤波器中的估计精度有限必然会造成融合误差的出现。

3 基于空间域组合观测的SLAM算法

3.1 基于空间域划分的SLAM模型

依据上文对集中式和分布式两种SLAM算法流程的分析,本文借鉴了集中式和分布式两种SLAM结构的优势,综合利用分布式结构降低计算量和计算复杂度以及提升容错性的优点,同时结合集中式结构在单步估计中精度较高的优势,设计了基于空间域划分的分布式SLAM算法。

依据SLAM系统模型的可观测性可知,当同时观测到非共线的两个特征点时,才能保证SLAM模型具有较好的可观测性[14]。本文将分布式的结构进行相对集中化的改进,对于每个子滤波器不是仅仅引入单个路标点作为观测量,而是在每步计算过程中,选取两个不共线的特征点组合成观测量,这样既能发挥在处理少观测点时集中式粒子滤波的精度优势,又能发挥分布式结构处理多观测点时降低计算复杂度的作用。

具体实现原理是:针对传感器所观测的整个空间,依据两个路标点与机器人连线之间的夹角θ,将整个观测空间中的路标点进行区域划分,保证其共线的可能性最低。假设机器人传感器测量的路标点情况如图2所示,则将传感器观测到的整个空间划分为几个子空间域A-A',B-B', C-C',如果路标点个数为偶数,每个空间域内包含两个不共线的路标点。而路标点个数为奇数时,将出现一个包含单个路标点的子空间域。

空间域划分实现流程如下:

步骤1 将激光传感器输入的原始数据转化为路标点信息。机器人通过激光传感器扫描前方180°范围内的障碍物,在返回值中筛选t时刻范围内的路标点z(t)={m1,m2,…,mn}。

步骤2 匹配t时刻与t-1时刻路标点并判断是否为新加入路标点。对比t-1时刻路标点集,设定邻域Δ=,根据最小邻域法进行两个时刻的路标点匹配,若在邻域内则认为t时刻与t-1时刻所测量的信息来源于同一路标点,否则视为新观测到的路标点。

步骤3 按照角度划分空间域。机器人与路标点的相对位置如图2所示,定义路标点方向角度θi为:在水平面内,由0°开始沿逆时针方向旋转到第i个路标点所在位置所形成的角度。

图2 空间域划分处理示意图

假设对应的角度分布范围为[θmin,θmax],分步将路标点划入不同子空间域中,将第n次划分后未被划分的路标点按照对应角度从小到大排列,构成有序集,同时,定义每次划分过程中,将划分为一个子空间域,剩余路标点再次重复上述过程。例如:经过第一次划分后,剩余的路标点有序集合变为θ1={θ1,θ2,…,θi-2,i∈Ν*},将其中的{θ1

min,θ1

mid}划分入一个子空间域中。依照上述算法流程,设经过n步划分之后则将剩余路标点划归同一个子空间域,至此划分过程结束。

步骤4 空间域模型的建立。将每个子空间域中的所有路标点组合成一个观测向量建立观测方程,从而基于各子空间域构建各子滤波器的组合观测模型,最终构建基于空间域划分的分布式SLAM系统方程如式(13)所示。

其中,k=1,2,…,n表示第k个子空间域。

基于上述空间域划分方法建立的各子空间域及对应的系统方程,对各子系统的滤波器进行设计,各子滤波器的设计均采用集中式滤波结构如式(14):

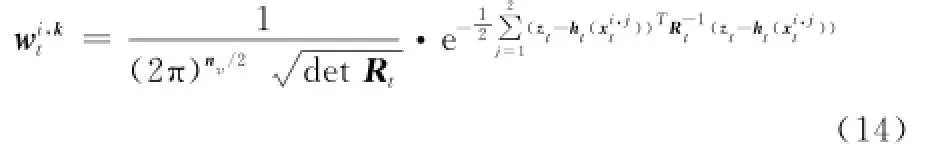
对于子滤波器的融合,采用分布式滤波结构,对量测信息进行融合如式(15):

式中,Mk为所划分的子空间总数。

从式(13)可以看出,本文提出的分布式SLAM结构中的机器人位姿估计部分仍然是非线性模型,因此将采用分布式UPF完成对机器人位姿的估计[15]。由于估计的过程中位姿估计和路标点估计是分别进行的,高概率情况下完成估计的位姿可近似认为是机器人的准确位置,结合传感器的测量信息可以计算出路标点近似精确值,此时路标点则可以被认为是静态的,路标点的估计模型可以简化为

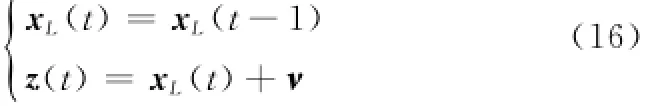
式中,xL(t)为t时刻的路标点位置;v为观测噪声。

从式(16)可以看出,路标点的估计过程转换为了一个线性过程,完全可以采用FKF完成对路标点的估计和更新。基于空间域划分的SLAM系统框图如图3所示。

图3 基于空间域划分的分布式SLAM系统

3.2 动态重构过程分析

在分布式SLAM算法的计算过程中,随着机器人的运动,某些路标点可能不再出现在观测范围内或是观测到新的路标点,如图4所示。此时,所对应的子空间域将重构,对应的子滤波器的状态量和观测信息需要进行舍弃或更新,从而会引起整个分布式系统的动态重构,该动态重构过程必然会带来系统重构误差,导致分布式SLAM系统的稳定性和鲁棒性问题。本文所采用的模型结构能够充分利用UPF对于粒子分布的调整作用,利用空间域内没有经历动态重构的路标点进行量测更新,有效地改善粒子分布,提高了系统的稳定性和鲁棒性。

从图4中可以看出,在机器人运行过程中,路标点变化情况主要会有如下3种类型:

(Ⅰ)在t时刻已经匹配成功,在t+1时刻仍可以观测并且匹配成功,如图4中路标点A-A'。

(Ⅱ)在t时刻匹配成功,但是在t+1时刻没有再观测到该路标点,如图4中路标点B-B'。

(Ⅲ)在t时刻没有观测到,而在t+1时刻第一次观测到并匹配成功,如图4中路标点C。

图4 空间域内路标点类型

(1)对于类型Ⅰ中的特征点,各子滤波器中正常采用UPF完成对机器人位姿的估计,采用无迹变换按如下过程实时更新滤波器中的粒子:

步骤1 进行粒子的初始化,利用先验分布{xi0,i=0, 1,2,…,N}在每个子滤波器中产生粒子群,并通过无迹变换选取粒子

步骤2 时间更新,把每个粒子对机器人状态估计的扩展向量分别代入机器人运动模型和路标点观测模型得到每个粒子的一步预测状态向量和一步预测观测向量根据每个粒子的权系数,计算每个子滤波器中所有粒子的状态向量的一步预测加权和和观测向量的一步预测加权和z-j

t|t-1。

步骤3 量测更新,对于预测的粒子分布情况,需要加入量测更新过程,从而根据实测路标点更新粒子状态分布:

(2)对于类型Ⅱ的特征点,若子滤波器中仍有其他路标点能够被观测到,则利用此路标点构建单路标点观测的子滤波器继续进行估计及重构,该结构有利于新加入特征点的初始化,设jL为滤波器中仍能够观测到的路标点,当新的路标点进入空间域,此类jL可以为其提供先验概率分布。

(3)对于类型Ⅲ特征点,若除了重构的路标点外,子滤波器仍能够通过空间域内的第Ⅱ类路标点进行量测更新过程,则子滤波器中的粒子分布情况由本次量测的路标点进行调整,那么式(19)中的一步预测误差zi,jt|t-1-z-jt|t-1的量测更新采用式(20)进行计算:

通过使新加入路标点继承未参与重构的路标点粒子分布的方法,能够充分利用Ⅱ类特征点提供的量测信息达到优化调整粒子分布的目的,而普通的分布式SLAM中新加入的路标点则只能通过新建立子滤波器进行初始化,收敛时间过长,影响系统的精度。此外,如果新加入的路标点不被纳入存在jL类型路标点的子空间域内,则以此路标点为基础建立的新滤波器,初始化后等待下一步观测重复式(19)的过程。

空间域中的粒子调整算法主要是利用无迹变换,从原先状态分布中按某一规则提取一些点,将这些点带入非线性函数中,取得相应的非线性函数点集,最后通过求取变化后的均值和协方差进行粒子调整。从而在路标点的更替过程中,单一路标点对应单个子滤波器在路标点丢失或加入时面临的子滤波器重构问题得以改善,从而改善系统的整体性能。

4 仿真实验

本文采用澳大利亚悉尼大学研究人员测得的实际数据[17]进行仿真实验,该数据是由车辆穿过维多利亚公园内各种不同区域,利用车辆自身装配的里程计和激光测距传感器获取车辆的当前里程信息和车辆距路标点(树)之间的距离,并同步使用GPS系统获得车辆位置信息。

在本文的仿真实验中,分别采用基于分布式UPF的分布式SLAM(distributed unscented particle filer-SLAM, DUPF-SLAM)与本文提出的基于空间域划分的分布式SLAM(distributed unscented particle filer-SLAM based on subspace,SDUPF-SLAM)分别进行估计,两种算法的仿真结果如图5所示。其中,虚线为DUPF算法的估计结果,实线为SDUPF算法的估计结果。星号为GPS数据,由于公园内树木遮挡存在GPS覆盖盲区,因此GPS数据并不连续。

图5 两种算法的估计结果与GPS数据对比

根据上述实验结果可以看出,SDUPF算法与DUPF算法相比,在粒子数目相同的前提下,随着车辆运动时间的增加,DUPF算法的精度逐渐变差。在初始阶段,两者的估计精度相差不大,SDUPF算法精度稍高,随后GPS信号被遮挡,当再次接收到GPS信号时(x=35.92 m,y=61.45 m,图中G1标识处),随后的一段时间内,DUPF估计的位置在x方向上明显偏离GPS数据达3.53 m(图中G2标识处),而SDUPF算法仍能很好地跟踪车辆的位置轨迹,在x和y轴方向偏离均小于1 m。当车辆再次接收到GPS信号时(x=66.34 m,y=75.02 m,图中G3标识处),此后SDUPF算法的跟踪效果要优于DUPF的结果(图中G4标识处),如图5中所示。因此,可以证明采用空间域划分的SDUPF算法的位姿估计精度明显高于DUPF算法。

为了对比两种算法的估计误差,本文采用式(21)对于实验结果中进行误差分析,给出两种算法在整个车辆定位过程中的估计结果和GPS数据之间在x方向以及y方向上的平均误差值如表1所示。由表1可知,在整个估计过程中,x方向和y方向上均是SDUPF的估计结果误差更小。

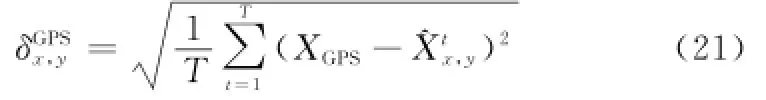
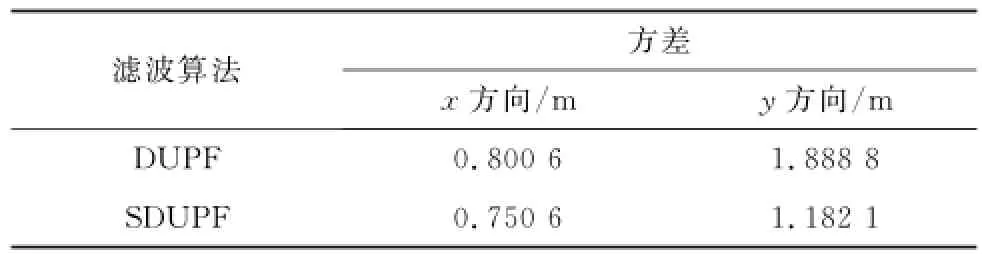
表1 估计结果与GPS数据的平均误差

在初始阶段GPS有效时,两种算法的估计误差如图6所示。其中,虚线为DUPF算法估计误差,实线为SDUPF估计误差。从图6中可以看出,从滤波估计初始阶段6.5 s开始,SDUPF算法估计结果在x方向以及y方向上误差均低于DUPF算法的估计误差。可见SDUPF的初始滤波估计精度就高于DUPF算法。

图6 滤波初始阶段与GPS的误差

5 结论

针对SLAM算法实现过程中存在的问题,本文提出了一种基于空间域划分的分布式SLAM算法,该算法先将观测到的路标点划分到各个子空间域,并依据子空间域构建组合观测模型,以分布式UPF和FKF分别实现机器人位姿和路标点的实时估计。同时,在每个子滤波器中利用无味变换的方法进行粒子分布的调整,利用空间域中无需重构的路标点进行粒子调整可以有效减少子滤波器的重构次数,该算法不仅借鉴了分布式结构可以使每个滤波器计算量下降,增强容错性的特点,又同时具备了集中式粒子滤波器在单步估计上的精度优势。仿真结果表明,本文提出的基于空间域划分的分布式SLAM算法的定位精度优于DUPF算法,并能够有效减少DUPF在长时间运行后由于子滤波器退化严重及重构次数增多造成的精度和稳定性问题。

[1]Durant W H,Bailey T.Simultaneous localization and mapping: part I the essential algorithms[J].Robotics and Automation Magazine,2006,13(2):99-110.

[2]Guivant J,Nebot E.Optimization of the simultaneous localization and map building algorithm for real time implementation[J].Proceedingsof the IEEE Transactions of Robotics and Automation, 2001,17(3):242-257.

[3]Csorba M.Simultaneous localization and map building[R].Oxford:University of Oxford,1997.

[4]Smith R C,Cheeseman P.On the representation and estimation of spatial uncertainty[J].Robotics Research,1986,5(4):231-238.

[5]Julier SJ,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceeding of the IEEE Aerospace and Electronic Systems,2004,92(3):401-422.

[6]Bolic M,Djuric P M,Hong S,et al.New resampling algorithms for particle filters[C]∥Proc.of the IEEE International Conference on Robotics and Automation,2003:589-592.

[7]Montemerlo M,Thrun S,Koller D,et al.RBPF-SLAM:A factored solution to the simultaneous localization and mapping problem[C]∥Proc.of the National Conference on Artificial Intelligence,2002:593 598.

[8]Montemerlo M,Thrun S,Koller D,et al.RBPF-SLAM 2.0:animproved particle filtering algorithm for simultaneous localization and mapping that probably converges[C]∥Proc.of the International Conference on Artificial Intelligence,2003:1151-1156.

[9]Won D,Chun S,Sung S,et al.INS/SLAM system using distributed particle filter[J].International Journal of Control, Automation and Systems,2010,8(6):1232-1240.

[10]Pei F J,Wu M,Zhang S M,Distributed SLAM usingimproved particle filter for mobile robot localization[J].The Scientific World Journal,2014:DOI:10.1155/2014/239531.

[11]Pei F J,Wu M,Zhang S M.Advanced distributed unscented particle filter for simultaneous localization and mapping[J]. WIT Trans.on Engineering Sciences,2014,86:DOI:10. 2495/ICFCIT131101.

[12]Thrun S,Burgard W,Fox D.Probabilistic robotics[M].Cambridge,MA:MIT Press,2006:148 151.

[13]Hlinka O,Hlawatsch F,Druric P M.Distributed particle filtering in agent networks[J].IEEE Signal Processing Magazine,2013,30(1):61-78.

[14]Perera L D L,Eric Netteleton.On the nonlinear observability and the information form of the SLAM problem[C]∥Proc.of the IEEE International Conference on Intelligent Robots and Systems,2009:2061 2067.

[15]Farahmand S,Roumeliotis S I,Giannakis G B.Set-membership constrained particle filter:distributed adaption for sensor network[J].IEEE Trans.on Signal Processing,2011,59 (9):4127-4135.

[16]Zhu Z Y.The algorithms and implementation for particle filters[M].Beijing:Science Press,2010:37-39.(朱志宇.粒子滤波算法及其应用[M].北京:科学出版社,2010:37-39.)

[17]Jose G.Victoria Park[EB/OL].[2013-10-18].http:∥www-personal.acfr.usyd.edu.au/nebot/victoria_park.htm.

Distributed simultaneous localization and mapping algorithm based on partition of space-region

PEI Fu-jun1,2,CHENG Yu-hang1,2,LI Hao-yang1,2,JU He-hua1,2
(1.School of Electronic Information&Control Engineering,Beijing University of Technology,Beijing 100124,China; 2.Beijing Key Laboratory of Computational Intelligence and Intelligence System,Beijing 100124,China)

To solve the problem of the simultaneous localization and mapping(SLAM)under the complex circumstance,a distributed algorithm of the SLAM based on partition of space-region is proposed considering the respective advantages of centralized configuration and distributed structure.The region is formed according to the angle between two landmarks and the robot,which is designed in case of the collinearity between two landmarks.The landmarks in each region are combined to establish the corresponding observation model.Besides,the position of the robot is obtained by applying the distributed unscented particle filter and the positions of the landmarks are estimated simultaneously by employing the Kalman filter.Meanwhile,the accuracy and the stability are improved through constructing the adjustment of particle distribution during the dynamic reconfiguration process.Eventually,the better real-time capability and filter accuracy of the proposed SLAM algorithm are proved through simulation experiments which are supported by actual data.

simultaneous localization and mapping(SLAM);partition of space-region;distributed structure;dynamic reconfiguration

TP 242.6

10.3969/j.issn.1001-506X.2015.03.26

裴福俊(1976-),男,副教授,博士,主要研究方向为惯性导航、自主导航及信息融合。

E-mail:PFJ@bjut.edu.cn

程雨航(1990),男,硕士研究生,主要研究方向为机器人自主导航算法。

E-mail:chengyuhangzxl@sina.com

李昊洋(1989-),女,硕士研究生,主要研究方向为机器人自主导航算法。E-mail:2548590420@qq.com

居鹤华(1969),男,教授,博士,主要研究方向为机器人自主导航控制。

E-mail:juhehua@bjut.edu.cn

网址:www.sys-ele.com

1001-506X(2015)03-0639-07