一道数学中考题的美学价值研究

●陈 平 (富阳区鹿山中学 浙江杭州 311400)

●盛志军 (富阳区郁达夫中学 浙江杭州 311400)

一道数学中考题的美学价值研究

●陈 平 (富阳区鹿山中学 浙江杭州 311400)

●盛志军 (富阳区郁达夫中学 浙江杭州 311400)

数学是美丽的，但数学的美丽是一种“冰冷的美丽”.为了让这份“冰冷的美丽”在学生面前熠熠生辉，数学教师应尽可能激起学生进入“火热的思考”，培养学生热爱数学、学习数学的热情.这种火热的“数学思考”和数学美的欣赏，是数学课程标准所要求学生达成的数学学习目标之一，也是赋予教师教学的一项根本任务.完成任务就需要教师在教学中不断探寻教学内容的美、数学思想和方法的美.为此，我国著名数学教育家张奠宙提出了帮助学生欣赏数学美的4个层次:美观、美好、美妙和完美，努力提升数学的美学价值，最终实现数学教学目标［1］.

2014年浙江省杭州市的一道中考数学题，是学生认识数学美学价值的好材料.笔者不局限于探求这道题的“学术形态”，而是从“教育形态”出发，通过挖掘数学的美学思想，提高数学学科能力和思维能力.

题目菱形ABCD的对角线 AC，BD相交于点 O，，BD=4，动点P在线段BD上从点B向点D运动，PF⊥AB于点F，四边形PFBG关于BD对称，四边形 QEDH与四边形PFBG关于 AC对称.设菱形ABCD被这2个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，BP=x.

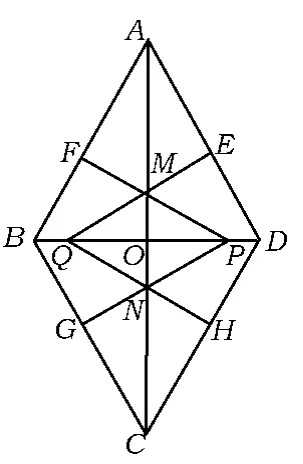
图1

1)用含x的代数式分别表示S1，S2;

2)若S1=S2，求x的值.

1 条件观察，在美观的图形欣赏中加深感知

这是一道集几何、代数和三角函数知识于一身的综合题.在教学中引导学生审题是首要工作.学生看题就像看卡通一样，首先引入眼帘的显然是美观的轴对称图形.为此，教师顺应学生的认知特点，紧紧抓住图形的轴对称性，再利用文字给出的条件，帮助观察、分解、感知有密切相关的轴对称图形(如图2).通过数形结合，弄清问题的显性条件、隐性条件和需要解决的问题.

1)观察①，菱形ABCD是轴对称图形.

2)观察②，由四边形PFBG关于BD对称，四边形QEDH与四边形PFBG关于AC对称.因此，又观察④，知△PFB与△PGB关于BP对称;观察⑤，△QDE与△QHD关于QD对称.

3)观察③，四边形AEMF与四边形CHNG关于BD对称，又它们各自关于AC对称.

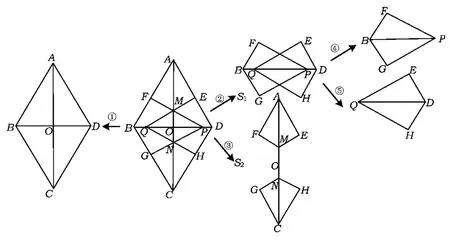
图2

由此可见，观察能让学生感受到本题把轴对称性的美表现得淋漓尽致，显示出数学独特的魅力.同时，在教学中，通过师生和生生的合作，让学生宏观上感知该题构建的框架，为进一步探究打下基础.

2 经验回溯，在美好的知识回顾中积极思考

有了观察打下的基础，接下来教师不应急于求成，而应让学生根据观察到的图形和题目给出的条件，回顾已有的学习经验和已形成的旧认知结构，细细品尝，流连忘返于美好的数学内容并投入到积极思考中.下列一些知识与技能，由教师适当、适时地点拨，让学生储存在头脑中的有关该题显性的、隐性的美好信息不断激活和涌现，并逐步梳理:

1)从条件菱形ABCD出发，得AB=BC=CD= DA;AO=CO，BO=DO，AC⊥BD;∠BAC=∠BCA=∠DCA=∠DAC……

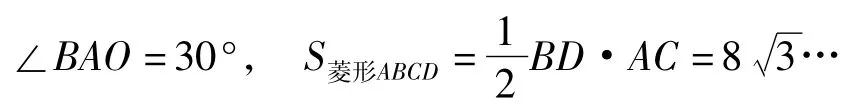
3)从条件PF⊥AB于点F，BP=x出发，可得

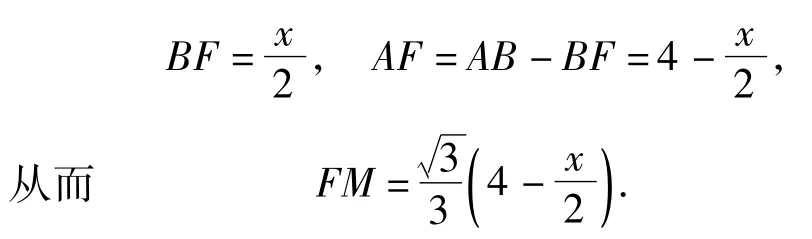
4)又由图形的对称性可知

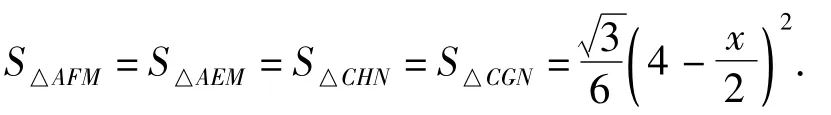
通过上述分析，菱形的性质得到了充分彰显，等边三角形的判定和性质得到了充分运用，直角三角形性质的作用得到了充分发挥，三角函数等重点知识和技能得到了充分回顾.与此同时，教师从图形和条件出发，从不同路径引领学生层层演绎推进，深入思考.学生在美好数学的体验、感受、熏陶下，素养得到了良好地提升.

3 问题探究，在美妙的整体分解中促进生成

从问题的结构上看，第1)小题是函数式的构建问题;第2)小题是方程问题.考查学生的函数和方程思想，本身是数学中一件美好的事情.教师如何引领学生探究这2个问题，这是本题的核心.而本题中蕴含的图形整体与部分的关系是解决问题的美妙玄机.

美妙1S1，S2表示什么?学生显而易见，S1表示菱形ABCD被这2个四边形盖住部分的面积，S2表示未被盖住部分的面积.菱形ABCD整体的面积是S1+S2(如图3).

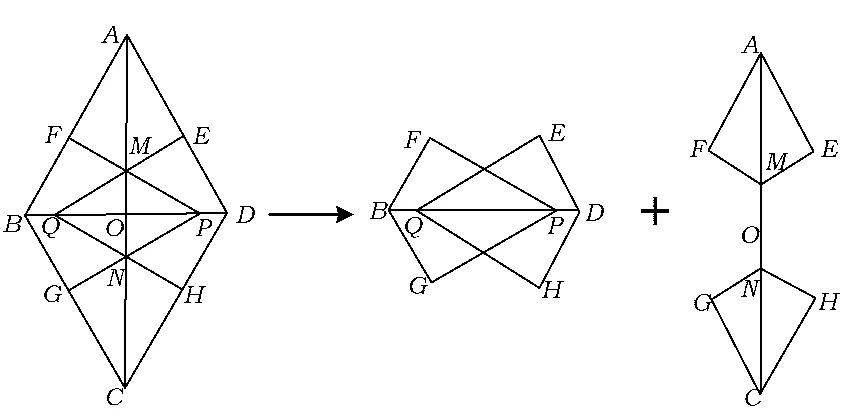
图3

美妙2怎样用含x的代数式表示S1.直接法很难表示S1，只能用间接法:

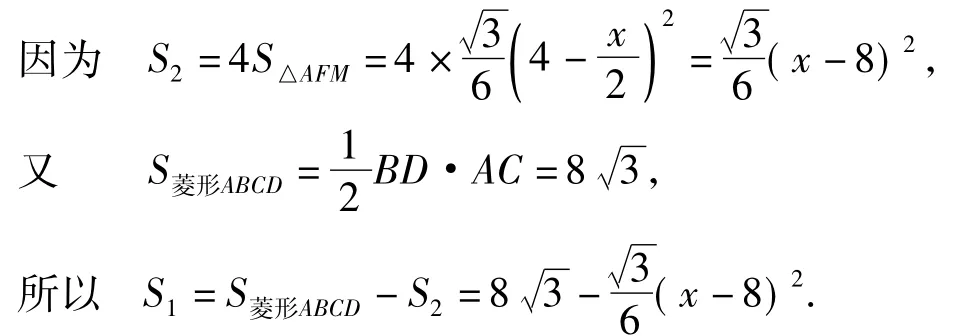
上述2个等式“S菱形ABCD=S1+S2，S2=4S△AFM”是解题的关键，美妙的事物存在于客体之中，需要教师帮助学生去再创造.而等式

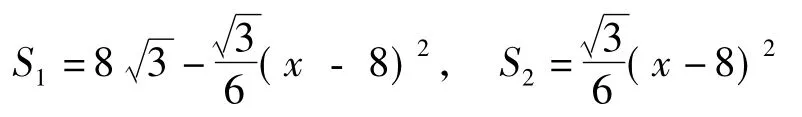
都是关于x的二次函数关系式.它们由形到数转化，也正是数学要寻求的美妙之处.

4 结论追寻，在思考动点运动问题中达到完美

本题给出的图形仅仅是为学生数学思考的一个方面的直观提示，并没有“如图”2个字.因此在审题上:一方面要让学生面对此类题型在细节上引起重视，以增强学生全面性思考问题的的意识，说明该题需要分类讨论;另一方面，让学生明确分类讨论是一种数学思想，如何分类达到问题解决，要有一种有效的方法.为此，把学生的关注点聚焦在“动点”上.

不妨这样启发学生:

1)如何理解“动点P在线段BD上从点B向点D运动”?

2)动点P从点B出发，终点到了哪里?经过什么特殊点?在这个过程中覆盖面积怎样变化?

3)在“BP=x”中，x是一个什么量?作为一个变量，是怎样变化的?

通过上述3个问题的引领，呈现如下2个图形(如图4和图5所示)，并由此确定x的取值范围.

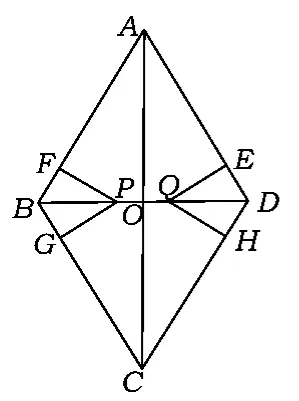
图4

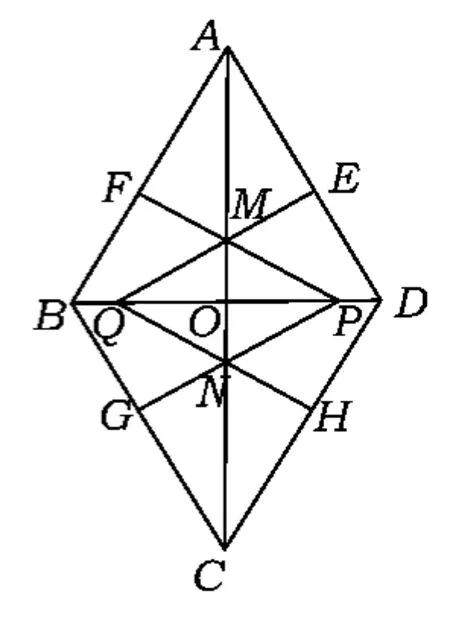
图5

而当0＜x≤2时，覆盖面积部分容易直接用含x的代数式来表示.由此，师生一起完美解答第1)小题:

1)①当点P在BO上，即0＜x≤2时(如图4所示).因为四边形ABCD是菱形，，BD= 4，所以

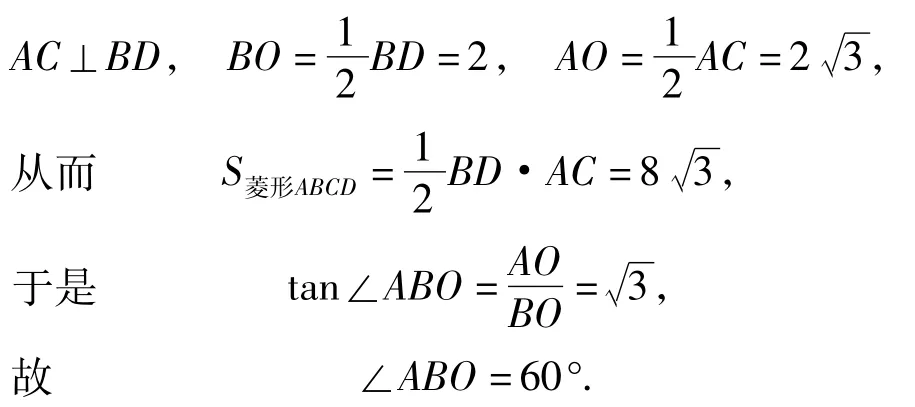
(或通过勾股定理求出AB=4=BD，又因为AB= AD，所以△ABD为等边三角形，故∠ABO=60°.)

在Rt△BFP中，因为∠BFP=90°，∠FBP= 60°，BP=x，所以

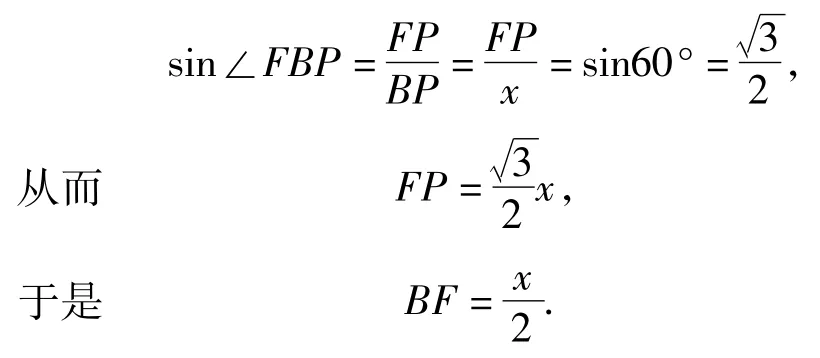
又因为四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称，所以

因为四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称，所以

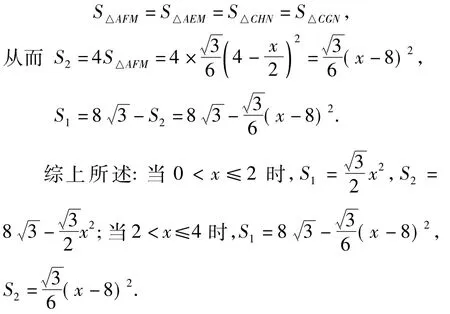
至于第2)小题，相应地给出2种情况予以解答，不难得到如下结论:

当点P在BO上，即0＜x≤2时，S1=S2的情况不存在;当点P在OD上，即2＜x≤4时，若S1= S2，则x的值为.

5 二次开发，在拓展中走进更美的数学境地

上述第2)小题，利用分类讨论，完美地考查了方程思想以及不等式范围内的取值问题.然而，二次开发该题的课程资源，是提升审美价值的有效途径.为此，我们反思该题的整个探索过程，发现四边形盖住部分的面积为S1，未被盖住部分的面积为S2，其实都是关于x的二次函数.

因此，教师不妨把本题的研究衍生到函数的有关性质中去，把学生带进更美的数学境地.在原题的基础上，再设计以下2个问题:

3)若动点P在线段BD上从点B向点D运动，当覆盖面积S1达到最大时，求S1与菱形ABCD的面积之比.

4)若动点P在BD延长线上运动时，覆盖面积为S1.问:S1是否存在最大值?如果存在，求出这个最大值和自变量x的取值范围;如果不存在，请说明理由.

解存在.因为动点P在BD延长线上运动时，x＞4.而PF⊥AB于点F，因此

①当点F与点A重合时，适合关系式

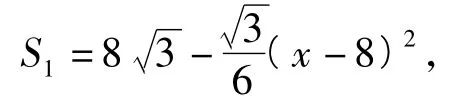
当x=8时，S1取得最大值.

②当点F在BA的延长线上时，S1的最大值恒为.此时，x＞8.

综上所述，S1的最大值是，自变量x的取值范围是x≥8.

从审美的角度出发，把握“美观、美好、美丽和完美”的整个探究过程，层层递进，火热思考，让一道“冰冷的美丽”的中考数学题，尽显光彩.既激发了学生学习数学的兴趣，增强了积极自信的态度，也达到了本题所要求的数学知识与技能学习目标，强化了简单化、数形结合、方程和函数、分类讨论等数学思想以及相应的数学方法，大大提高了学生的思维水平和数学问题解决的能力.

参考资料

［1］张奠宙，李士锜，李俊.数学教学导论［M］.北京:高等教育出版社，2003:158-224.