妙用判别式巧解数学题

●建 (华市第一中学 浙江华 321015)

妙用判别式巧解数学题

●金建军(金华市第一中学 浙江金华 321015)

一元二次方程根的判别式是方程知识的核心内容，是联系3个“二次”(二次函数、二次方程与二次不等式)的重要桥梁.运用判别式解数学题，关键在于构造函数根(零点)的一元二次方程，然后利用Δ≥0来求解;或构造恒大于(或小于)0的二次不等式，然后利用Δ≤0来证明.现举几例，以飨读者.

1 判别式在等式与不等式中的应用

1.1 解方程(组)

例1若 x，y∈R，满足2x－2x2y2－2y(x+ x2)－x2=5，则x= ______，y =______.

(2013年浙江省高中数学竞赛试题)

解把等式看成关于x的一元二次方程

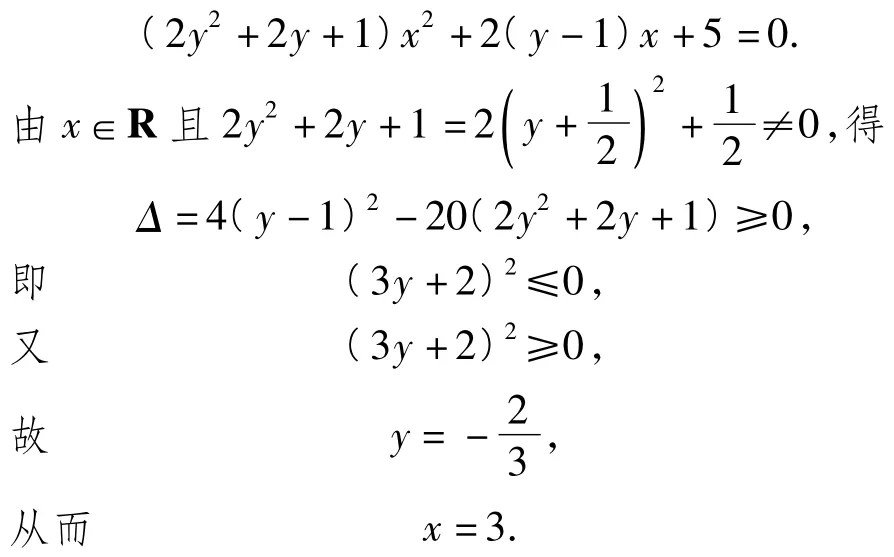
例2试求满足方程x2－2xy+126y2=2 009的所有整数对(x，y).

(第6届东南地区高中数学竞赛试题)

解设整数对(x，y)满足方程

将其看作关于x的一元二次方程，则

由题意知Δ的值应为一个完全平方数.若y2＞42，则Δ＜0;若y2＜42，则y2可取0，12，22，32，相应的Δ值分别为8 036，7 536，6 036和3 536，它们都不是平方数.因此，仅当 y2=42时，Δ=500(42－y2)+36=62为完全平方数.

当y=4时，方程(1)可化为x2－8x+7=0，解得x=1或x=7;当y=－4时，方程(1)可化为x2+ 8x+7=0，解得x=－1或x=－7.

综上可知，满足原方程的全部整数对为:(1，4)，(7，4)，(－1，－4)，(－7，－4).

点评利用主元变换，妙用Δ≥0，巧解方程.

1.2 证明等式

例3如果 a，b，c，d都是实数，且 a2d2+ b2(d2+1)+c2+2bd(a+c)=0，求证:b2=ac.

证明把等式整理成关于x的一元二次方程

点评构造方程，妙用判别式，借助非负数使问题顺利解决.

练习1已知实数a，b，c满足a=6－b，c2= ab－9，求证:a=b.

证明由已知式得

练习2已知(z－x)2－4(x－y)(y－z)=0 (其中x≠y)，求证:2y=x+z.

证明构造以(x－y)，(z－x)，(y－z)为系数的一元二次方程

由根与系数的关系可知

1.3 证明不等式

例4 已知α+β+γ=π，求证:

证明视不等式的左边减去右边为一个关于x的二次函数，则

其判别式为

故开口向上的二次函数f(x)恒为非负，即对所有的x，y，z，所求证的不等式成立.

点评本题通过构造关于x二次函数，利用判别式与二次函数的图像关系使问题得到妙解.

例5 已知正实数x，y满足x+y=1，求证:

证明设，则

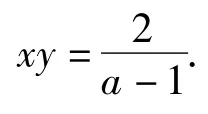
点评利用换元法，妙用判别式，使问题得到巧证.

练习3 已知实数a，b满足a2b2+a2+6ab+ 2a+9=0，求证:.

解将a2b2+a2+6ab+2a+9=0按a的降幂排列，可得

可见x=a是一元二次方程(b2+1)x2+(6b+ 2)x+9=0的1个实根，于是

练习4 已知，求证:y2≥4xz.

解据题意，只需证y2－4xz≥0，而此形式类似于一元二次方程的判别式.现将已知方程化为

1.4 求最值

例6 若实数x，y满足4x2+y2+xy=1，则2x+y 的最大值是______.

(2011年浙江省数学高考理科试题)

解设2x+y=t，则y=t－2x，将其代入4x2+ y2+xy=1，得

点评此类二元二次方程求最值的问题，很多都可以用判别式法来处理，尽管4x2+y2+xy=1和方程6x2－3tx+t2－1=0都有2个未知量，但用最大值t代替其中一个未知量y，离目标更近了，使用判别式后只有一个未知量t，达到消元的目的，非常有效!

练习5 若实数x，y满足x2+y2+xy=1，则x+y 的最大值是______.

(2011年浙江省数学高考文科试题)

练习6已知实数a＞0，b＞0满足a+2b+ ab=30，试求ab的最大值.

解设ab=y，则，由题设得

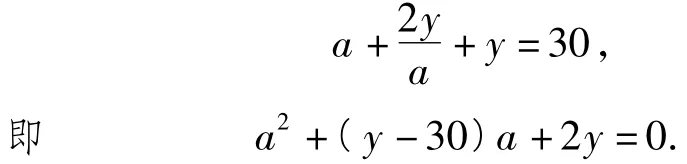
由Δ=(y－30)2－8y≥0，解得y≤18或y≥50.又由正实数a，b满足a+2b+ab=30知ab＜30，则当y=18时，a=6，b=3，ab取得最大值18.

点评把a2+(y－30)a+2y=0看成关于a的二次方程，Δ≥0只是方程在(0，+∞)上有解的必要条件，要经检验才能说明最值的取得.

练习7已知实数x＞0，y＞0满足x+2y+ 2xy=8，则x+2y的最小值是 ( )

(2010年重庆市数学高考理科试题)

解设x+2y=t，代入x+2y+2xy=8消去x得

由Δ=4t2－16(8－t)≥0，解得t≥4或t≤－8，经检验:t≤－8不合题意，故x+2y的最小值是4，选B.

练习8若正数x，y满足x+3y=5xy，则3x+ 4y的最小值是 ( )

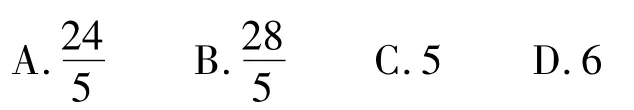
(2012年浙江省数学高考文科试题)

解略(答案:C).

1.5 求取值范围

例7若知a2+b2≥λ(a+3b+1)对任意a，b∈R恒成立，求λ的取值范围.

解把已知式整理成关于a的二次不等式

对任意a∈R恒成立，则

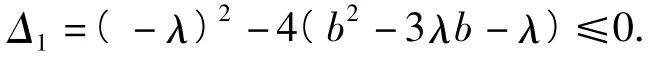
把上式整理成关于b的二次不等式

对任意b∈R恒成立，则

点评本题是多变量不等式恒成立问题，由定义域为R，结合二次函数图像，直接运用判别式Δ求解，涉及“主元思想”，虽然本题涉及的是不等式，但仍可运用判别式的原理.

练习9对于函数若f(x)存在x∈R使函数f(x)=x成立，则称x为函数f(x)的不动点.已知f(x)=ax2+(b+1)x+(b－1)(其中a≠0)对任意实数b，函数f(x)恒有2个相异的不动点，求a的取值范围.

解依题意，f(x)=x有2个不同实根，即ax2+bx+b－1=0有相异实根，故a≠0，且

对任意b恒成立，因此

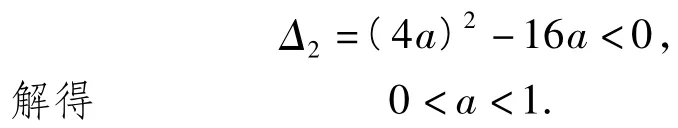
2 判别式在函数值域中的应用

点评分子、分母中的最高次为2次的分式函数可以考虑用判别式法求值域.

练习10如图1，某地有3家工厂，分别位于矩形ABCD的2个顶点 A，B及CD的中点 P处，AB= 20 km，BC=10 km.为了处理这3家工厂的污水，现要在该矩形区域上(含边界)且与A，B等距的一点O处建造一个污水处理厂，并铺设3条排污管道AO，BO，PO.记铺设管道的总长度为y km.

图1

1)按下列要求建立函数关系式:

①设∠BAO=θ(rad)，将y表示成θ的函数;

②设OP=x(km)，将y表示成的x函数.

2)请你选用第1)小题中的一个函数关系确定污水处理厂的位置，使铺设的污水管道的总长度最短.

(2008年江苏省数学高考理科试题)

点评本题选择函数模型②求含根式函数的最值问题，转化为方程有解，运用判别式体现反函数思想、变量相互表示思想、等式等价变形思想.

3 判别式在三角、向量中的应用

点评本题通过观察已知等式与所证不等式的结构，构造一个二次函数，使解题过程变得简洁，但要求较高.

点评由韦达定理知，方程的根必定是正根，判别式只要保证有实根即可.

4 判别式在数列中的应用

例11设a1，d为实数，首项为a1、公差为d的等差数列{an}的前 n项和为 Sn，满足 S5S6+ 15=0.求d的取值范围.

(2010年浙江省数学高考理科试题)

点评因为a1为实数，所以本题利用构造关于a1的二次方程求解.

5 判别式在解析几何中的应用

例12如图2，已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的2倍且经过点M(2，1)，平行于OM的直线l在y轴上的截距为m(其中m≠0)，l交椭圆于2个不同的点A，B.

图2

1)求椭圆的方程;

2)求m的取值范围.

x2+2mx+2m2－4=0．

由直线l与椭圆交于2个不同的点A，B，得

Δ=(2m)2－4(2m2－4)＞0，

从而m的取值范围是{m|－2＜m＜2，m≠0}．

点评在处理直线与圆锥曲线的位置关系及取值范围的问题中，要注意利用判别式来解决.

从上面的例子可以看出解决此类问题的关键是:从条件出发构造出关于某个变量的一元二次函数，进而通过判别式来求解问题.它对解决双变量或多个变量的问题尤其有效，当然在处理问题的过程中要特别注意问题的等价性.