基于未补偿偏置滤波器的惯导动态初始对准

何虔恩，高钟毓，吴秋平

（清华大学 精密仪器系，北京 100084）

基于未补偿偏置滤波器的惯导动态初始对准

何虔恩，高钟毓，吴秋平

（清华大学 精密仪器系，北京 100084）

动态初始对准是惯性导航系统（惯导）工程应用的重要功能之一。针对动态环境下随机干扰和弱可观惯性仪表误差导致对准滤波器性能下降的问题，采用未补偿偏置滤波器实现惯导系统的初始对准。给出了带高度阻尼的惯导水平通道误差模型，根据最小二乘估计原理定量分析了陀螺漂移误差对降维滤波器精度的影响，进而推导出带偏置结构的对准误差模型，设计出基于水平位置误差观测的7维未补偿偏置Kalman滤波器。动态试验结果表明，未补偿偏置滤波器能有效提高惯导动态初始对准性能，仅需40 min对准精度即达标，比直接降维滤波器快一倍以上，具有较强的工程应用价值。

惯性导航系统；初始对准；动态条件下；Kalman滤波；未补偿偏置滤波

惯导是一种航位推算系统，其工作精度依赖于初始条件的设定精度。例如，为达到0.1 n mile/h的导航精度，初始水平和方位失准角应分别小于6"和30"，且初始速度误差应小于0.1 n mile/h。因此，为获得高精度的性能，系统必须具有高精度的初始化[1]。其中，初始位置和速度通过全球卫星定位系统等外部设备容易直接获得，并且在水平速度阻尼条件下，初始位置和速度误差的影响将逐渐衰减为零（经过1～2个Schuler振荡周期）；而初始水平角和方位角通常需要借助特定的算法间接计算出来，并且其误差对导航精度的影响是长期的（高精度惯导通常是无方位阻尼的）。因此，系统初始对准的主要任务在于获得精确的初始水平角和方位角。

长航时高精度惯导是复杂的光机电系统，在长期工作过程以及动态环境中各种冲击、振动的作用下，其零部件难免会出现故障，在故障修复后，要求系统能够即刻恢复正常工作状态。此时，动态初始对准是系统不可或缺的功能之一，其基本要求是保精度、速度快。

惯导有光学对准法、传递对准法和自对准法等初始对准方法[1]。其中，自对准法简便、可操作性强，且适用于动基座，因而取得广泛应用。目前，自对准主要采用基于现代控制理论的滤波法。现代滤波法采用状态空间法描述系统误差的动态特性，可同时估计初始失准角和可观测的惯性仪表误差参数，并能最优（在某种意义下，如方差最小）地过滤各种动态干扰。国内外学者结合不同的应用背景，有针对性地开发了各种滤波算法。例如，针对非线性问题，有扩展Kalman滤波[2]、无迹Kalman滤波[3]和粒子滤波[4]等算法；针对随机干扰，有鲁棒滤波[5]、H∞滤波[6]和自适应滤波[7]等算法。这些算法通常对惯性仪表误差和测量偏置进行精确建模，并将模型参数作为滤波器状态给予估计（增广状态法）。然而，在动态条件下，由于风浪、发动机振动和运载体机动等多种因素的综合作用，惯导所遭受的随机干扰可能比静态条件下大2倍以上。此时，惯性仪表误差和测量偏置相关状态的可观测性弱，增广状态法无法在短时间内获得其精确估计（根据惯导误差传播特性[1]和实践经验知，欲精确分离高精度惯性仪表误差参数，滤波时间通常要超过12 h，这无法满足动态初始对准的快速性要求）；同时，将降低滤波收敛速度，并可能导致滤波器发散。若直接忽略惯性仪表误差和测量偏置的影响（直接降维法），则可能引入较大的模型误差，降低滤波器性能。针对这类矛盾，Zanetti R等[8-9]提出未补偿偏置滤波器的思想：将偏置和噪声的影响统一视为不确定源，并利用偏置结构的特点有针对性地、实时地调整滤波器的过程和测量噪声阵，使滤波器性能接近最优（滤波计算得到的样本协方差与状态估计误差协方差匹配）。

将未补偿偏置滤波器思想应用在惯导动态初始对准中，旨在解决惯性仪表误差（陀螺漂移误差达到1×10-3(°)/h量级）和动态随机干扰导致降维滤波器性能下降的问题。本文研究了惯性仪表误差对失准角初值估计精度的影响；在此基础上，设计相应的未补偿偏置滤波器；最后，给出基于未补偿偏置滤波器的动态初始对准试验结果，并与增广状态法和直接降维法的结果进行了比较，得到有关结论。

1 系统误差模型及对准误差分析

1.1 系统误差模型

引入高度阻尼后，惯导垂直通道的误差可忽略不计，此时，对于低速巡航载体，水平通道的误差方程可写为[1]：

式中：δrN, δrE——位置误差的北向和东向分量；

δvN, δvE——速度误差的北向和东向分量；

ωD=-ωiesinL ，ωie和L分别为地球自转角速率和本地地理纬度；

ω——Schuler振荡角频率，1.24×10-3rad/s；

sg——本地重力加速度值；

▽N, ▽E——比力误差的北向和东向分量；

ψN, ψE——平台失准角的北向和东向分量，满足如下关系式：

式中：λ——相对地理经度，初始时刻为0；

S1, σ1, γ2——由地球坐标系（e系）依次绕x、y和z轴旋转到空间稳定平台坐标系（P系）的三个Euler角；

ΔS1, Δσ1, Δγ2——平台分别沿x、y和z方向的失准角，考虑陀螺漂移误差，经推导可得其近似的解析表达式为：

式中：S10、Δσı、Δγ——平台失准角初值；

Δε1x,Δε1y,Δ2z——陀螺常值漂移误差；

Δd22——陀螺g2项漂移系数误差。

1.2 对准误差分析

选择水平位置误差为观测变量，并记观测向量为

式中：ra——地球平均半径。

对于低速运载体，在对准期间经纬度变化为小量。简单起见，考虑S1和σ1为小量的情况，此时，式(2)可简化为：

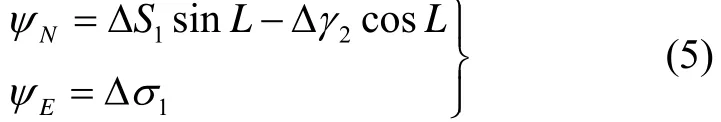
另外，为满足快速性要求，时间t通常较小。此时，式(3)可简化为：

这里，已利用γ2≈ωiet+γ20和

将式(6)代入式(5)，再与式(4)一同代入方程(1)，整理后可得：

易见，式(8)等号右边是关于时间t的二次多项式。在提供一定长度观测数据的条件下，可分离出各项系数。若不考虑陀螺漂移误差（采用直接降维法），则初始对准将只包含式(8)第一等式的常值项、t1项以及第二等式的常值项和部分t1项（与Δσı相关的部分），按照最小二乘估计原理，可推导出如下对准结果（中低纬度地区）：

根据式(7)(9)可得陀螺漂移误差在对准误差中的贡献如表 1所示。可见，陀螺漂移误差主要造成方位对准误差。由表 1知，Δδ10和Δε1ycosγ20-Δε1xsin γ20主要引起常值型方位对准误差，其它漂移系数误差主要引起与对准时间成正比的方位对准误差（t1型误差）。由于失准角初值本身是定常的，常值型的对准误差是无法消除的；而t1型的对准误差，通过采取一定的技术措施（如增广状态法），有可能减小甚至被消除。

表 1 陀螺漂移误差在对准误差中的贡献Tab.1 Alignment errors caused by gyroscope drift errors

2 未补偿偏置滤波器设计

2.1 带偏置结构的误差模型

根据第1节的讨论（详见式(9)和表1）知，为了提高对准精度，陀螺漂移误差组合参数δSt、δσ0和tγδ是值得考虑的。此时，根据式(3)和式(6)有：

式中：F(t)——7×7维系统矩阵，各个元素根据式(1)、式(2)和式(10)容易得到（限于篇幅，不一一列出）；

B(t)——7×3维偏置矩阵，第i行第j列元素Bij为（i=1,2,…,7，j=1,2,3）：

其余元素为零；

w(t)——7×1维状态噪声向量。

以水平位置误差为观测量，观测方程可写为

式中：H——2×7维观测矩阵：

n(t)——2×1维观测噪声向量。

由第1.2节的讨论知，基于水平位置误差观测，状态x(t)是可观的，因此定能设计出有效的滤波算法对其进行估计。

2.2 对准滤波器设计

令状态噪声w(t)和观测噪声n(t)为相互独立的零均值Gauss白噪声，且协方差阵满足ε

δ为与w(t)和n(t)不相关的随机常向量，且满足

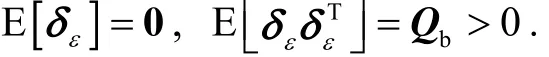
时间传播：

滤波增益：

测量修正：

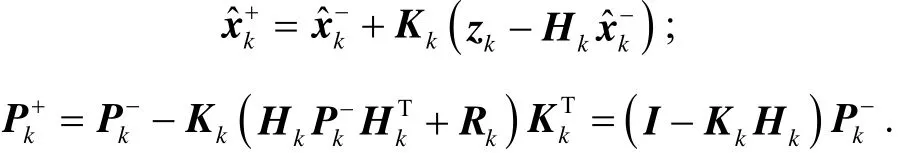
Lk递推计算：

这里：Φk,k-1≈I+F（tk-1）·Δt ，I为7阶单位阵，Δt为采样周期；Bk≈B（tk）·Δt ；Qk≈Q（tk）·Δt ；Rk=R（tk）。

3 试验结果

3.1 对准结果

某惯导系统在纬度为9º～23º的区域进行了海上动态试验。利用在线记录的系统试验数据和外参考数据（如：全球定位系统提供的经纬度信息），对上述滤波算法进行验证。这里，人为引入1×10-3(º)/h量级的陀螺漂移误差。

图1摘录了某段试验数据（载体速度和加速度计随机噪声的幅值分别达0.2～0.6 m/s和0.4～1 m/s2）分别采用未补偿偏置法（UBM—Uncompensated Bias Method）、直接降维法（DRM—Directly Reduced Method）和增广状态法（ESM—Extended States Method）的对准结果。图1中，ρ 表示允许的对准误差。

由图1易见，未补偿偏置滤波法的对准速度和精度优于直接降维法和增广状态法——水平和方位对准仅分别进行10 min和40 min即达到指标要求。在陀螺漂移误差和随机干扰的影响下，直接降维法需要多一倍以上的时间才能使方位精度满足要求（如δS10所示）；而增广状态法则由于陀螺漂移误差组合参数的可观测性差，对准速度在三种方法中最慢。

图 1 动态初始对准初值误差收敛曲线Fig.1 Convergence curves of initial errors for initial alignment under dynamic conditions

3.2 导航结果

初始对准进行1 h后转入导航，三种对准方法相应的归一化导航经纬度误差如图2所示。易见，未补偿偏置滤波法对应导航误差的24 h周期分量依次比直接降维法和增广状态法小1倍和3倍以上，这与前面的对准结果是一致的。另外，经度误差的趋势项和纬度误差的24 h周期发散振荡分量分别由赤道和极轴陀螺的常值漂移误差（取决于陀螺逐次启动的重复性精度）引起，这对系统长时间的工作精度具有致命的影响，必须采取一定的技术手段（如重调）来消除。

图2 归一化经纬度误差Fig.2 Normalized errors of longitude and latitude

以上试验结果与前述理论分析相吻合，在一定程度上验证了未补偿偏置滤波法应用在惯导动态初始对准中的有效性。

4 结 论

针对动态环境下随机干扰大、惯性仪表误差可观测性弱问题，采用未补偿偏置滤波器实现惯性导航系统的初始对准。定量分析了陀螺漂移误差对降维滤波器精度的影响，在此基础上给出带偏置结构的对准误差模型，并设计了7维未补偿偏置滤波器。动态试验结果表明，未补偿偏置滤波器能有效对付动态随机干扰和惯性仪表误差的影响，其对准速度比直接降维滤波器快一倍以上，仅需40 min使对准精度达标，具有较强的工程应用价值。

值得注意的是，限于快速性要求，动态初始对准无法解决惯性仪表逐次启动重复性误差导致系统长时间导航精度下降的问题。因此，在导航阶段必须采取有关技术措施，如重调，对惯性仪表误差进行标校，以保证系统长时间导航精度达标。

（References）：

[1] 高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012: 184-389. Gao Zhong-yu. Inertial navigation systems technology [M]. Beijing: Tsinghua University Press, 2012: 184-389.

[2] Fang J, Yang S. Study on innovation adaptive EKF for in-flight alignment of airborne POS[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(4): 1378-1388.

[3] Lubin C, Baiqing H, AN L, et al. Strapdown inertial navigation system alignment based on marginalised unscented Kalman filter[J]. IET Science, Measurement & Technology, 2013, 7(2): 128-138.

[4] Mao B, Wu J. An adaptive particle filter for MEMS based SINS nonlinear initial alignment[C]//Proceedings of the 2010 International Conference on Information and Automation. 2010: 1504-1509.

[5] Sun F, Lan H, Yu C, et al. A robust self-alignment method for ship's strapdown INS under mooring conditions [J]. Sensors, 2013, 13(7): 8103-8139.

[6] Guo Lei, Cao Song-yin, Qi Chun-tang, et al. Initial alignment for nonlinear inertial navigation systems with multiple disturbances based on enhanced anti-disturbance filtering[J]. International Journal of Control, 2012, 85(5): 491-501.

[7] Fang J, Han X. In-flight alignment algorithm based on ADD2 for airborne POS[J]. Journal of Navigation, 2013, 66(2): 209-225.

[8] Zanetti R, Bishop R. Kalman filters with uncompensated biases[J]. Journal of Guidance Control and Dynamics, 2012, 35(1): 327-330.

[9] Hough M. Orbit Determination with improved covariance fidelity, including sensor measurement biases[J]. Journal of Guidance Control and Dynamics, 2011, 34(3): 903-911.

Initial alignment based on uncompensated bias filter for inertial navigation systems under dynamic conditions

HE Qian-en, GAO Zhong-yu, WU Qiu-ping
(Department of Precision Instruments, Tsinghua University, Beijing 100084, China)

The initial alignment of inertial navigation system(INS) under dynamic conditions plays a key role in the engineering applications. In this paper, an uncompensated bias filter is adopted in INS initial alignment to overcom the problem of alignment filter’s performance degradation due to random disturbances and inertial instrument errors of weak observability under dynamic conditions. An INS horizontal error model with altitude damped is presented, and the effect of gyro drift errors on accuracy of reduced alignment filter is analyzed quantitatively according to the principle of least squares estimation. Consequently, an alignment error model with bias structure is derived and a seven-dimension Kalman filter with uncompensated bias based on observations of horizontal position errors is designed. Results of dynamic experiments show that performance of INS initial alignment under dynamic conditions can be improved effectively by using the Kalman filter with uncompensated bias, in which the expected alignment accuracy is achived within 40 min, and the speed is at least one fold faster than that of direct dimension-reduction filters, showing great value in engineering applications.

inertial navigation system; initial alignment; dynamic condition; Kalman filter; uncompensated bias filtering

U666.1

A

1005-6734(2015)02-0184-05

10.13695/j.cnki.12-1222/o3.2015.02.009

2014-11-23；

2015-03-02

总装“十二五”预研项目（51309030401）

何虔恩（1985—），男，博士后，研究方向为导航系统与控制。E-mail：heqianen2005@126.com

联 系 人：吴秋平（1972—），男，副研究员，博士生导师。E-mail：wuqiuping@mail.tsinghua.edu.cn