高精度LINS陀螺采样频率以及噪声抑制技术
2015-06-05李汉舟张娟妮王朝光
李汉舟,张娟妮,潘 泉,王朝光,邓 麟
(1. 西北工业大学 自动化学院,西安 710072;2. 航天科技集团第16研究所,西安 710100)
高精度LINS陀螺采样频率以及噪声抑制技术
李汉舟1,2,张娟妮2,潘 泉1,王朝光2,邓 麟2
(1. 西北工业大学 自动化学院,西安 710072;2. 航天科技集团第16研究所,西安 710100)
基于激光陀螺高带宽和数字化输出的特点,提出激光陀螺数字信号处理的两个基础性问题,采样频率合理性与抗混叠滤波。分析了国产高精度激光捷联惯导常用的2000 Hz采样频率下激光陀螺频谱特性。指出在该采样频率下,激光陀螺输出信号中存在某些固定频率干扰信号。提出一种逐步升高采样频率的方法,给出了谱峰位置确定公式,证明国产高精度激光陀螺输出信号中存在机抖频率的 3倍频和5倍频干扰信号,并给出合理的最低采样频率应为4500 Hz。为了解决激光陀螺数字化输出的抗混叠滤波问题,建议引入过采样技术,继续提高采样频率,降低激光陀螺功率谱密度,并利用低通滤波抑制噪声,提高激光陀螺精度。
激光陀螺;采样频率;激光捷联惯性导航系统;抗混叠滤波;过采样
随着激光惯性导航系统(Laser Inertial Navigation System, LINS)精度不断提高,有必要对其噪声和干扰信号进行深入分析,以便在现有惯性仪表精度基础上,进一步发挥LINS性能。
由于光学元件上各点的非均匀损耗和散射,当激光陀螺输入角速率较小时,输出频率差将消失,这被称为闭锁效应。为消除闭锁效应,目前工程上广泛采用机械抖动偏频方案。该方案利用交变的机械抖动机构,对激光腔整体施加高频抖动激励,在机械抖动作用下减小了闭锁误差[1]。由于激光陀螺输出信号中抖动信号能量一般会远远大于有用信号能量,在导航运算之前,必须设法滤除抖动信号,提高信噪比,得到载体真实运动信息,滤波效果的好坏直接影响导航精度。因此,很多学者把注意力都集中在信号处理上技术[2-3],却忽略了所有数字信号处理方法能够正常发挥作用的前提条件——正确采样。
对于LINS,有两个关于采样的基本问题需要商榷:
① 最低采样频率的确定:国产高精度激光陀螺的抖动频率低于 450 Hz,如果仅仅需要把抖动频率滤除,根据采样理论,对于正弦信号的采样和恢复,最低采样频率等于正弦信号频率的两倍即可,也就是说理论上高精度LINS的采样频率大于900 Hz即可。国内高精度激光陀螺的采样频率fs一般都取2000 Hz,该参数似乎符合采样定理,所以很少有人怀疑其合理性。本文就此问题设计了采样试验,证明该采样频率并不合理,应该设置的更高一些。
② 采样信号混叠问题:采样理论要求在fs/2处的干扰噪声能量要很小,否则高于fs/2以上的信号能量会混叠进基频带。对于传统机械转子陀螺,力矩器本身就是一个低通滤波器,起到一定滤波作用。另外,其输出的模拟信号可以在采样前,通过有源或无源滤波器进一步把高频干扰衰减掉。因此传统机械陀螺的采样和量化过程,可以很容易地满足采样理论。而激光陀螺直接输出经过量化的数字信号,无法设置常规的有源或无源抗混叠滤波器。这说明,如果用较低的频率直接对激光陀螺采样,那么在fs/2以上的噪声能量依旧很大,这部分能量将不可避免地混入基频带,引起一定干扰。
以上两个问题是LINS设计和使用的基础性问题,处理好这两个问题对进一步提高LINS精度具有重要意义。
1 高精度LINS陀螺信号谱分析
在LINS中,由于三个激光陀螺抖动信号互相干扰,每个陀螺输出信号中都含有其它两个陀螺的抖动信号,理想的谱分析结果是在每一个陀螺的谱线上仅有三个峰。实际测量果真如此吗?
以国内高精度LINS通常使用的fs=2000 Hz采样频率对激光陀螺采样,在采集数据时,LINS保持静止。图1给出了高精度LINS中三个激光陀螺原始脉冲数据谱分析结果。可以看出,国产高精度激光陀螺抖动频率在300~450 Hz之间。每个激光陀螺输出信号中,能量最强的是自身的抖动信号,幅值达到80 dB以上。除了自身抖动信号以外,每个激光陀螺都会受到其他两陀螺抖动信号的影响,抖动能量在40 dB左右。
由图1中还可以看到,除了三个最强的能量以外,因为没有抗混叠滤波器,激光陀螺在二分之一采样频率处仍然是能量较高的平直谱。每个激光陀螺的谱分析图上都不是理想的三个谱峰,而是有4到6个谱峰,这种现象几乎出现在笔者掌握数据的所有高精度LINS中。
表面上看,这些多出来的谱峰都在1000 Hz以内,通过数字滤波器,可以得到一定衰减,并不十分影响LINS精度。其实不然,由于在时域对信号的采样造成频域的延拓[4],图1所示[0,fs/2]的谱分析结果实际上是由[Nfs,Nfs+fs/2] (其中N=0,1,2…)频段正向叠加,以及[Nfs-fs/2,Nfs]频段对称叠加的总结果,因此尽管谱分析结果显示它们都在1000 Hz以内,但并不能确定它们到底在哪个频段,也就不能确定其真实频率到底是多少。这些多出来的谱峰绝对能量并不小,大一点的有30 dB,小一点的也有10 dB左右,都高于真实信号(直流分量)能量很多倍,必然导致激光陀螺信号干扰,产生导航误差(例如伪圆锥误差)。更为糟糕的是,这些干扰信号根本无法消除,因为它们没有被正确采样。
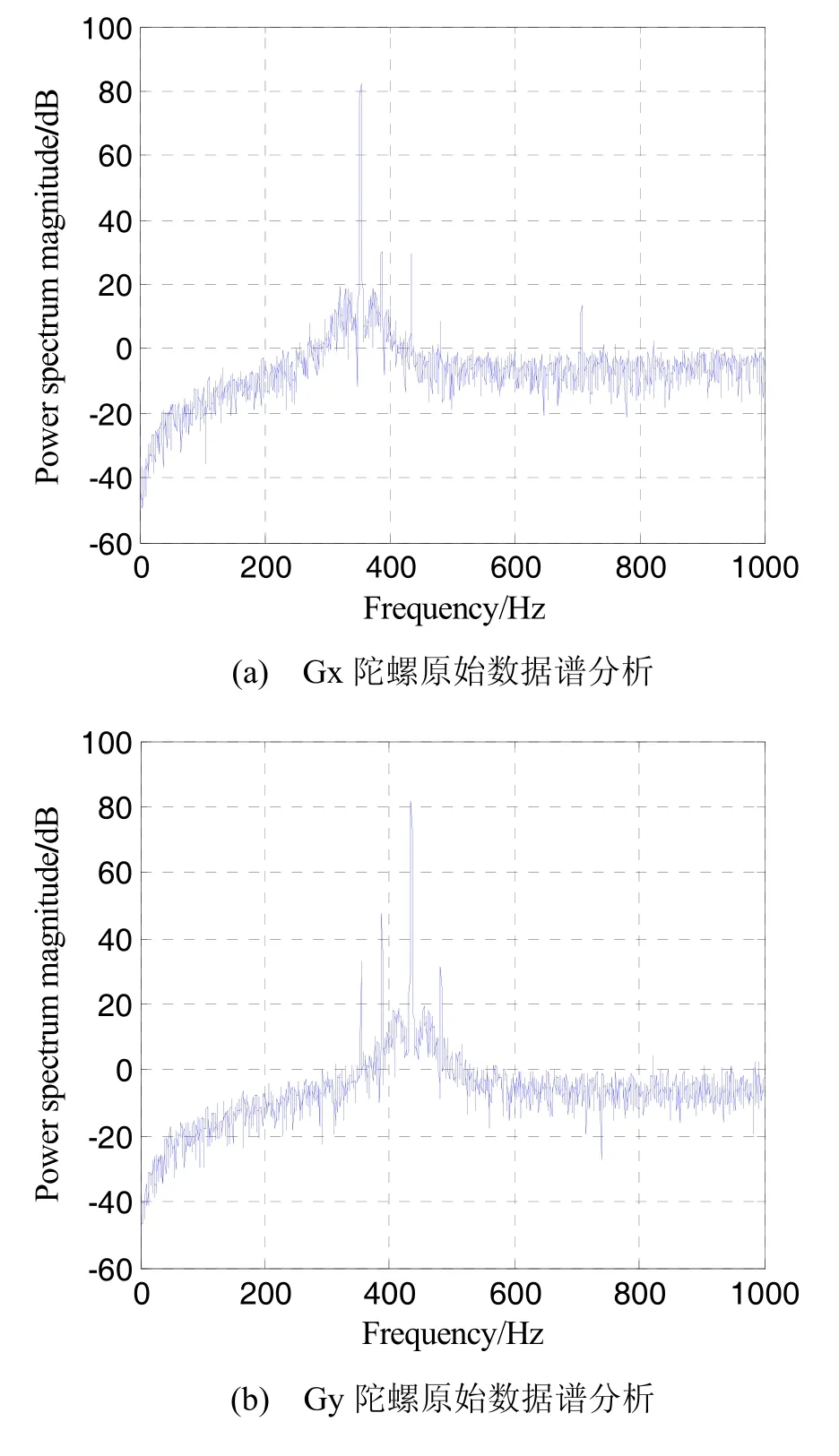

图1 LINS激光陀螺数据谱分析Fig.1 LINS laser gyro power spectrum analysis
2 干扰信号源的识别与处理方法

由于试验使用的LINS导航计算机速度有限,本文只选择了单陀螺进行试验,但是同样的方法也适用于LINS。对一个高精度激光陀螺分别进行2000 Hz、4000 Hz和20000 Hz的采样试验,采样时间序列和谱分析结果见图2。从图2(a)、(c)、(e)可以看出,随着采样频率的提高,正弦抖动信号越来越圆滑;每一个采样频率下的谱分析图中,机抖频率拥有最高的谱峰,相对高度约80 dB,说明激光陀螺中抖动信号能量是最大的,该陀螺抖动频率为364 Hz,如图2(b)所示。除了抖动频率以外,2000 Hz采样时,在50 Hz、180 Hz和908 Hz处还有尖峰;当提高采样频率到4000 Hz采时,除了抖动频率以外,依然有三个谱峰,但频率分别为50 Hz、1092 Hz和1820 Hz,如图2(d)所示;继续提高采样频率到20000 Hz时,同样在50 Hz、1092 Hz和1820 Hz仍然存在尖峰,如图2(f)所示。由(1)式可以断定,以2000 Hz采样时,180 Hz的干扰信号是由1820 Hz混叠形成的,而908 Hz的谱峰是由1092 Hz混叠形成的。这个试验说明在这块高精度激光陀螺输出信号中,除了机抖干扰以外还存在三个干扰源,其频率分别为50 Hz、1092 Hz和1820 Hz。
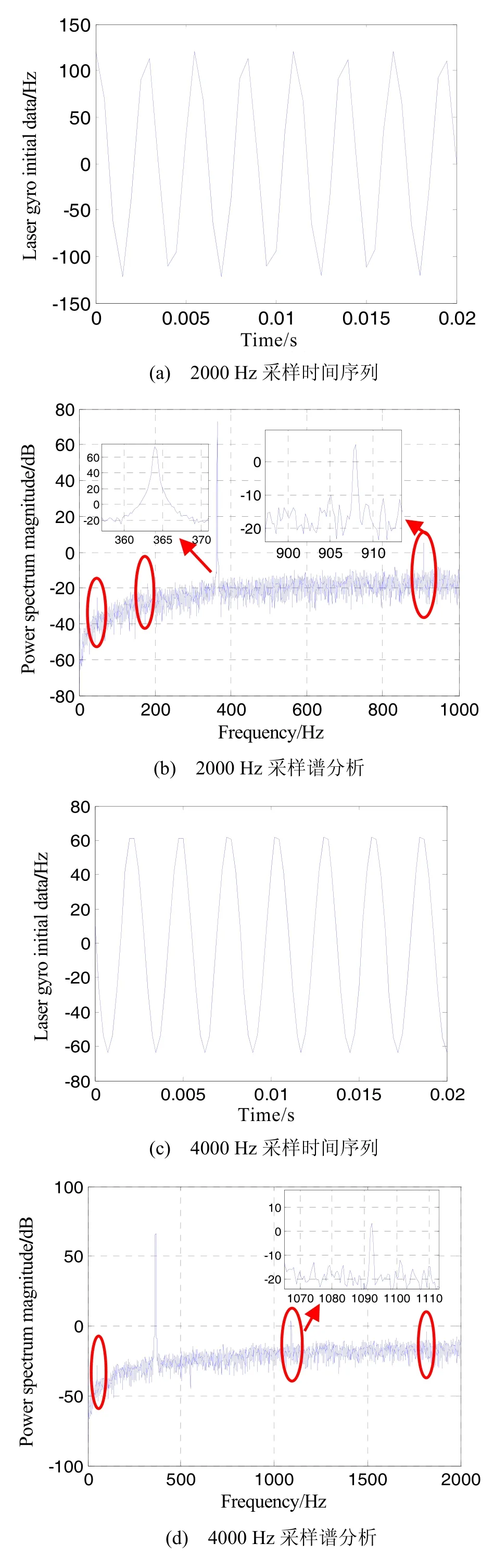

图2 高精度激光陀螺不同采样频率试验Fig.2 High-precision ring laser gyro experiments with different sample frequencies employed
那么,现在的问题是,除了能量最大的机抖信号,这三个干扰频率是从哪里来的?其物理意义是什么?又该如何消除?本文就这些问题讨论如下:
① 50 Hz工频干扰。该干扰信号是通过测试台、数据采集计算机将220 V供电电源频率耦合进入激光陀螺输出信号中的。因为50 Hz处于LINS通频带内,在三个陀螺输出信号中都有这一信号,除了造成数据波动以外,还会形成伪圆锥误差,影响LINS地面测试精度。所以在LINS地面测试时,对测试设备应给予足够重视,可采取的措施有:选择性能优良的一次电源给LINS供电;采用抗工频干扰电源、电源净化器或其它措施抑制一次供电电源带来的干扰;LINS与测试计算机之间采用光耦隔离,避免工频干扰通过测试计算机通讯接口窜入LINS;
② 1092 Hz干扰信号正好是机抖频率的 3倍(364×3=1092),该信号是机械结构频率特性与机抖信号耦合后产生的,由激光陀螺机械结构形式与材料特性决定,该干扰信号会随着机抖频率变化而变化,但始终是机抖频率的3倍。尽管文献[5]指出对高精度激光陀螺的机械结构已经进行了优化,但从试验结果看,3倍频信号依然强烈存在,在机械结构优化不能完全解决问题的情况下,可提高采样频率,把该信号采集进来,用信号处理的方法滤除;
③ 1820 Hz干扰信号是机抖频率的 5倍频信号(364×5=1820),该信号同样来自于激光陀螺的机械结构谐振,也是该型产品所固有的特征频率。抑制该频率干扰的有效方法同样是提高采样频率,把干扰信号正确采集进来,然后滤除。
从以上分析可见,后两种干扰信号都是由机抖信号引起的,是激光陀螺特有的干扰源。从本节分析可以断定,国内高精度LINS目前普遍采用的2000 Hz采样频率并不合理,在2000 Hz的采样频率下,导致基频带内混叠了3倍频和5倍频产生两个虚假干扰信号,这两个虚假干扰信号不仅造成激光陀螺数据异常波动,还会导致一定的伪圆锥误差,造成LINS精度损失。
因此,本文认为2000 Hz的采样频率对国产高精度LINS偏低,如果需要滤除5倍频引起的混叠,则按照最高机抖频率450 Hz估计采样频率至少应为:
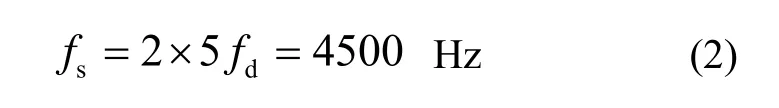
式(2)仅仅从滤除5倍频干扰角度,将采样频率提高到4500 Hz以上。理论上,继续提高采样频率,对激光陀螺形成过采样,还会进一步降低激光陀螺噪声。
3 激光陀螺的过采样
由于激光陀螺直接输出频率信号,无法在计数环节前设置有源或无源物理滤波器,也就无法按常规方法分析系统抗混叠滤波器的参数是否满足系统要求。从图2 (f)可知,即便将采样频率提高到20 kHz,在高频段激光陀螺谱线仍然是一个平直谱。这足以说明激光陀螺的带宽高于10 kHz。文献[6]指出,激光陀螺的带宽在30 kHz以上,这意味着,在0~30 kHz以内,激光陀螺自身信号衰减幅度不会小于 0.707倍。正因为激光陀螺拥有较高的带宽,从图1和图2中的所有谱分析图均可以明显看到,在 fs/2附近,噪声能量都高于有用信号(直流分量)。而采样定理要求在 fs/2处的噪声能量远小于有用信号。所以,用较低的频率对LINS采样必然把高频噪声引入基频带,造成一定混叠。为了解决这一矛盾,必须设法降低 fs/2以上频段信号能量。笔者认为一种比较可行的方法是进一步提高采样频率,对激光陀螺形成过采样。
现代高精度Σ-Δ型A/D的理论基础之一就是过采样技术。其主要思想是:通过提高采样频率,将均匀分布的噪声功率在[0,fs/2]内摊薄[7],从而降低采样噪声。当然Σ-Δ型A/D转换器除了提高采样频率以外,还使用了噪声整形技术,将基带内的噪声进一步降低。根据过采样理论,输入端信噪比SNR与过采样率M有如下关系:

式中:N为A/D位数。可见,对于A/D来说,采样频率提高4倍,相当于A/D位数提高1位,即精度提高1倍。
由于在高频采样条件下,激光陀螺中的噪声属于1/fr分形噪声[8-9],这种噪声功率随频率增加而降低,从图2的图(b)、(d)、(f)可见,在高频段,激光陀螺噪声分布类似于白噪声(属于1/fr分形噪声的一种),也是均匀分布。因此提高采样频率,除了可以减小高于[0,fs/2]频段的噪声能量,还可以把更多的噪声信号纳入基频带,然后通过滤波的方法衰减基频带噪声,也起到一定成型滤波的作用,从而提高激光陀螺精度。
4 结 论
本文针对国内高精度LINS采样频率合理性问题进行了分析讨论,通过试验数据说明,在国产高精度激光陀螺中存在机抖频率的3倍频和5倍频干扰信号。目前普遍采用的2000 Hz采样频率偏低,会引起一定的信号混叠,影响激光陀螺精度。指出激光陀螺的最低采样频率应该为4500 Hz。建议在系统硬件速度足够的条件下,继续提高采样频率,形成过采样,减小由于激光陀螺带宽过宽带来的噪声,通过低通滤波器进一步抑制激光陀螺噪声。
(References):
[1] Peshekhonov V G. Gyroscopic navigation systems: current status and prospects[J]. Gyroscopy and Navigation, 2011, 2(3): 111-118.
[2] Sin-Woo Song, Jae-Cheul Lee, Suk-Kyo Hong, et al. New random walk reduction algorithm in ring laser gyroscopes [J]. Journal of Optics, 2010(12): 1-8.
[3] Hua Chunhong, Ren Zhang, Zhang Minhu. Filtering of long-term dependent fractal noise in fi ber optic gyroscope[J]. Journal of Systems Engineering and Electronics, 2010, 21(6): 1041-1045.
[4] 姚天任. 数字信号处理[M]. 北京: 清华大学出版社, 2011: 345-412. Yao Tian-ren. Digital signal processing[M]. Beijing: TsingHua University Press, 2011: 345-412.
[5] 于旭东. 二频机抖激光陀螺单轴旋转惯性导航系统若干关键技术研究[D]. 长沙: 国防科技大学, 2011: 45-71. Yu Xu-dong. Research on some key technologies for single-axis rotation inertial navigation system with mechanically dithered ring laser gyroscope[D]. Changha: National University of Defense Technology, 2011: 45-71.
[6] Martin G J, Gillespie S C, Volk C H. The Litton 11 cm triaxial zero-lock gyro[C]//Position Location and Navigation Symposium. IEEE, Atlanta, USA, 1996 : 49-55.
[7] Wu J, Carley R. Electromechanical Σ-Δ modulation with high-Q micromechanical accelerometers and pulse density modulated force feedback[J]. IEEE Transactions on Circuits and Systems. 2006, 53(2): 274-287.
[8] 李汉舟, 潘泉, 王小旭, 等. 激光陀螺分形噪声的理论与实验研究[J]. 光电子·激光, 2012, 23(11): 2085-2088. Li Han-zhou, Pan Quan, Wang Xiao-xu, et al. Theoretical and experimental researches on the laser gyro fractal noise[J]. Journal of Optoelectronics· Laser, 2012, 23(11): 2085-2088.
[9] Skaloud J, Bruton A M, Schwarz K P. Detection and filtering of short-term (1/fγ) noise in inertial sensors[J]. Navigation, 1999, 46(2): 97-107.
Gyro sample frequency and noise restraint methods in a high-precision laser INS
LI Han-zhou1,2, ZHANG Juang-ni2, PAN Quan1, WANG Chao-guang2, DENG Lin2
(1. College of automation, Northwestern Polytechnical University, Xi’an 710072, China; 2. The 16th Institute of China Aerospace Science and Technology Corporation, Xi’an 710100, China)
Based on the characteristics of laser gyro’s high bandwidth and digital output, two basic problems in laser gyro digital signal processing are put forward, i.e. rational sampling frequency and anti-aliasing filter. The laser gyro spectrum characteristics in domestic high-precision laser strapdown inertial navigation are analyzed, and it is found that there are some fixed frequency jamming signals in the laser gyro output at 2000 Hz sampling frequency. A noise restraint method is put forward by gradually increasing sampling frequency to locate spectrum peak position, and the frequency calculation formulas are given. It is verified that there are 3 times and 5 times of dithering frequency interference signals in laser gyro output signal by using these formulas. The domestic high-precision laser gyro’s reasonable minimum sampling frequency is given, which should be 4500 Hz at least. In order to solve the problem of anti-aliasing filter, an oversampling technology should be used to reduce the power density of the laser gyro in frequency field. Meanwhile the low-pass filter should be employed to restrain noises and improve the laser gyro’s accuracy.
laser gyro; sampling frequency; laser inertial navigation system; anti-aliasing filter; oversampling
U666.1
:A
2015-05-09;
:2015-09-20
国家自然科学基金项目(61135001)
李汉舟(1973—),男,博士,研究员,从事高精度惯性导航系统、数字信号处理、机器视觉等研究。
E-mail:mr_lihanzhou@sina.com
1005-6734(2015)05-0585-05
10.13695/j.cnki.12-1222/o3.2015.05.006
