惯导平台自标定中安装误差可观性分析

许永飞，张士峰

（国防科学技术大学 航天科学与工程学院，长沙 410073）

惯导平台自标定中安装误差可观性分析

许永飞，张士峰

（国防科学技术大学 航天科学与工程学院，长沙 410073）

针对惯导平台连续翻滚自标定中安装误差标定精度不高这一现状，提出了一种解决方案。通过对惯性器件的输出误差模型和安装误差的分析，建立了系统的姿态动力学方程和观测方程，利用输出灵敏度理论分析了系统的可观性，指出加速度计安装误差可观性较差是影响标定精度的主要原因。利用 Kalman滤波中的估值方差矩阵计算了安装误差之间的相关系数，计算结果表明可观性差是由安装误差之间的线性相关性造成的，并确定了具体的不可观参数。以加速度计输入轴为基准建立平台坐标系可以减少安装误差项，使所有的安装误差的变得可观。最后的仿真结果表明在新的方案下，安装误差的估值偏差小于5"，标定精度得到了显著提高。

惯导平台；安装误差；可观性；输出灵敏度；相关系数

惯导平台广泛应用于舰船、潜艇、战略弹道导弹等需要长时间为载体提供高精度导航参数的场合。而惯性仪表的精度在很大程度上决定了惯导平台的使用精度。由于各种因素的制约，惯性仪表会存在各种误差，从而影响惯导平台的导航精度。因此各项误差进行标定和补偿就显得尤为重要[1]。

对于惯导平台的误差模型，美国的 Frazier J. Helling等以液浮陀螺惯导平台为背景建立了包含63项误差的误差模型[2]。该模型物理意义明确，具有较强的工程实用性。

对于惯导平台的标定，常用的有多位置自标定[3-4]和连续旋转自标定[5-7]两种方法。多位置标定实现起来简单，运算量小，易引入器件的安装误差以及对准误差等误差因素且能够标定的误差系数有限。连续旋转自标定实现起来复杂，但能够标定出更多的误差系数。在连续旋转自标定中，旋转轨迹的可观性分析及旋转轨迹的优化是重点和难点，在文献[7-8]中，PWCS理论、Lie导数、奇异值分解、输出灵敏度等方法被用于系统的可观性分析。

作者在基于文献[2]中的误差模型开展惯导平台连续旋转自标定的研究时发现，当考虑12项惯性器件安装误差时，安装误差标定结果不理想。灵敏度分析表明，安装误差存在不可观的问题，但不能确定具体的不可观参数。在此基础上，本文从随机变量的相关性出发，通过相关系数分析指出安装误差不可观是由不同安装误差之间的线性相关性造成的，需要舍弃三项加速度计安装误差才能保证所有的安装误差都是可观的，且舍弃的安装误差必须符合一定的规律：即应保证平台坐标系的一根坐标轴沿一个加速度计的输入轴方向。

1 基本理论

1.1 基本坐标系及转换关系

图1 平台几何构成示意图Fig.1 Platform geometry

图2 陀螺仪安装误差Fig.2 Platform-gyro coordinate geometry

图3 加速度计安装误差Fig.3 Platform-Accelerometer geometry

平台系到各惯性器件坐标系之间的转换矩为

平台坐标系到平台基座坐标系之间的坐标转换矩阵为

1.2 惯导平台误差模型

通过框架角建立惯导平台的动力学模型。框架角速率与平台角速率之间的关系为

老年教育属于服务型、社会性教育，对老年人的管理也是以人为本，本着关心、关爱和尊重老人的基本原则，最大限度满足老年人对兴趣爱好和教育内容的需要。老年大学和教育机构尽力为老年人提供便利舒适的教育环境，悉心、耐心、周到地为老年人提供优质和满意的服务。比如，将有共同爱好的老年人集中起来，互相交流沟通，找到精神的寄托，让老年人的子女安心工作，也填补了老年人因子女不在身边而牵挂思念的空闲时间，对于建立幸福家庭，发展社会文化事业起到了积极的作用［3］。

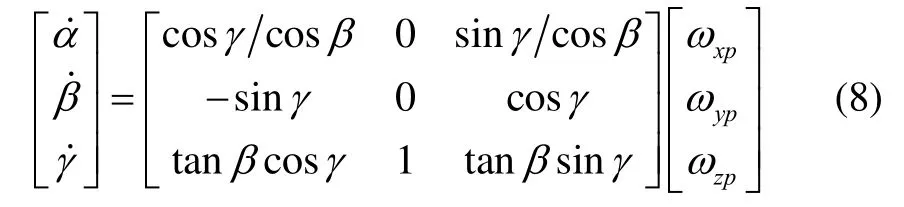
1.3 系统动力学方程与观测方程

将前文提到的所有的误差系数及三个框架角作为状态变量，则系统的非线性动力学方程可以表示为

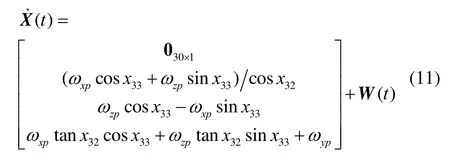
式中：W(t)表示系统干扰，为零均值的高斯白噪声。

选取三个加速度计的输出作为观测量，则系统的观测方程为

式中：m(t)为测量噪声。

1.4 灵敏度分析理论

如果系统用状态方程来描述，这时的灵敏度问题通常用所谓的轨迹灵敏度来处理，它是表征参数变化对状态影响的属性。具体来说，如果系统在额定参数时的额定方程为（假设参数为r维的）

式(15)与式(18)组成了状态灵敏度方程，不管原来的状态方程是否为线性的，状态灵敏度方程一定是线性的：

2 考虑12项安装误差时的标定结果

在连续旋转自标定中，惯导平台的翻转路径的设计是重点和难点，参考文献[7]的思路对旋转路径进行设计，根据设计结果对平台施加指令力矩，采集加速度计的输出，然后采用扩展卡尔曼滤波（EKF）方法对测量数据进行处理，获得误差系数的估计值。表 1给出了考虑12项安装误差（常规方案）时的标定结果。

从表1中可以看出陀螺和加速度计的零次项、一次项误差系数都获得了非常好的估计结果，但12项安装误差的估计结果较差，因此需要分析原因，给出解决这一问题的方法，以提高标定精度。

表1 考虑12项安装误差时的标定结果Tab.1 Calibration result of error parameters under conventional scheme

3 安装误差可观性分析

在旋转路径优化时，采用了系统的总可观测性矩阵的秩及其奇异值作为优化目标函数，这个目标函数并不能反映具体某个状态变量的可观测度。参数的输出灵敏度反映了参数在某个时间段内的激励程度，而参数输出灵敏度之间的相关特性也反应了激励的互相关特征，通过分析不同参数的输出灵敏度之间的联系可以进一步分析具体参数的可观测性。

图4给出了加速度计安装误差的输出灵敏度，从图中可以看出6个加速度计的安装误差的输出灵敏度存在两两近似互相关的情况，这表明需要去掉3个加速度计安装误差才能完全可观，这解释了加速度计安装误差估计结果较差的原因，但具体舍弃哪些安装误差还无法确定。图5给出了陀螺安装误差的输出灵敏度，从中可以看出每项安装误差都得到了充分的激励，且不存在近似互相关的情况。因此，需要从别的途径入手解释陀螺安装误差估计结果不理想的原因。

图4 加速度安装误差输出灵敏度Fig.4 Output sensibility of accelerometer misalignment angle

事实上，在Kalman滤波中，滤波方差阵除了可以用来分析滤波效果外，还可以用来分析各状态变量之间的相互影响关系。不同状态变量之间的相关系数可以通过下式得到

从表2中可以看出，陀螺安装误差之间的相互影响程度更大，而加速度计安装误差之间的相互影响关系要小一些。通过进一步的分析可以发现，6个陀螺安装误差之间的相关关系很大程度上是因为与3个加速度计安装之间的相关关系造成的。因此考虑在连续旋转自标定中舍弃这三项误差。

图5 陀螺安装误差的输出灵敏度Fig.5 Output sensibility of gyro misalignment angle

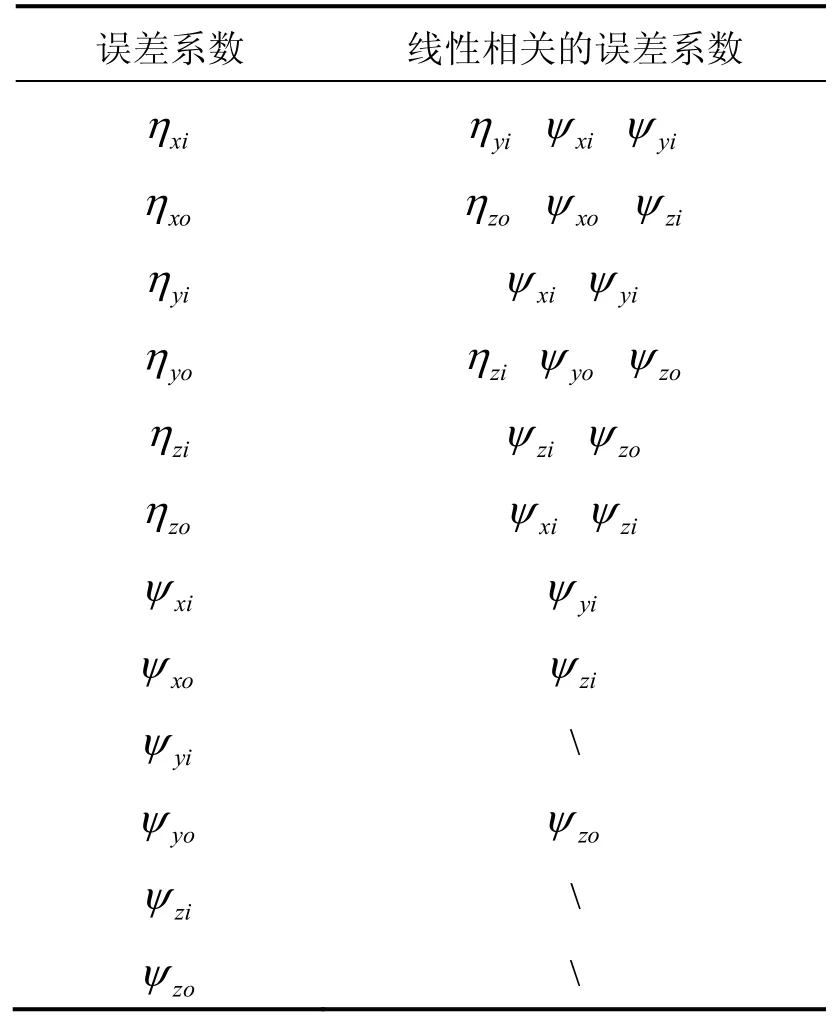
表2 安装误差之间的相关关系Tab.2 Correlation among misalignment angles

4 改进方案的标定结果

根据上述结论，在连续旋转自标定中略去3项加速度计安装误差即以X加速度计的输入轴为基准建立平台坐标系（改进方案）。依然采用与原方案一致的旋转路径、误差系数真值及滤波初始条件，图6给出了在新的方案下惯性器件安装误差的标定结果。

从图6中可以看出，采用改进方案后，惯性器件安装误差的标定结果得到了显著提高，估计误差小于5"。更进一步的分析与仿真表明，以任何一个加速度计的输入轴为基准建立平台坐标系，安装误差的标定结果都能获得很好的估计结果。

图6 新方案下安装误差标定结果Fig.6 Estimation results of misalignment angles under improved scheme

5 结 论

本文对惯导平台连续旋转自标定中惯性器件安装误差标定结果不理想的原因进行了分析，结果表明这是由于安装误差之间的线性相关性造成的。解决这一问题的方法是以加速度计的输入轴为基准建立平台坐标系。另外利用相关系数分析来确定不可观的状态变量，这为可观性分析提供了新的思路。

（References）：

[1] Seong-hoon P W, Farid G. A triaxial accelerometer calibration method using a mathematical model[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(8): 2144-2152.

[2] Frazier J. Hellings. Application of extended Kalman filtering to a dynamic laboratory calibration of an inertial navigation system[R]. AD-763718, 32-38.

[3] Zhang H L, Wu Y X, Wu W Q, et al. Improved multi-position calibration for inertial measurement units [J]. Measurement Science and Technology, 2010, 21(1): 015107.1-11.

[4] 包为民, 申功勋, 李华滨. 惯性平台在系统中多位置翻滚自标定方法[J]. 北京航空航天大学学报, 2011, 37(4): 462-465. Bao Wei-min, Shen Gong-xun, Li Hua-bin. Investigation on inertial platform multi-position rolling self-calibration [J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4): 462-465.

[5] 丁智坚, 蔡 洪, 杨华波, 等. 浮球式惯性平台连续翻滚自标定自对准方法[J]. 国防科技大学学报, 2015, 37(3): 148-154. Ding Zhi-jian, Cai Hong, Yang Hua-bo et al. Continuous self-calibration and self-alignment method for floated inertial platform[J]. Journal of National University of Defense Technology, 2015, 37(3): 148-154.

[6] 曹渊, 张士峰, 杨华波, 等. 惯导平台误差快速自标定方法[J]. 宇航学报, 2011, 32(6):1281-1287. Cao, Yuan, Zhang Shi-feng, Yang Hua-bo, et al. Research on rapid self-calibration method for inertial platform[J]. Journal of Astronautics, 2011, 32(6): 1281-1287.

[7] Cao Yuan, Cai Hong, Zhang Shi-feng, et al. A new continuous self-calibration scheme for a gimbaled inertial measurement unit[J]. Measurement Science and Technology, 2012, 23(1): 015103.1-12.

[8] Li Chan, Zhang Shi-feng, Cao Yuan. One new onboard calibration scheme for gimbaled IMU[J]. Measurement, 2013, 46(8): 2359–2375.

[9] 孟卫锋, 袁爱红, 贾天龙, 等. 高精度惯性平台十六位置自标定方案[J]. 中国惯性技术学报, 2015, 23(2): 150-155. Meng Wei-feng, Yuan Ai-hong, Jia Tian-long, et al. 16-position self-calibration of high-accuracy inertial platform[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 150-155.

Observability analysis of IMU’s misalignment angles in self-calibration for inertial platform

XU Yong-fei, ZHANG Shi-feng
(College of Aerospace science and engineering, National University of Defense Technology, Changsha 410073, China)

An improved scheme for inertial platform is proposed to solve the problem that the calibration accuracy for the misalignment angles is not high in the continuous rotation self-calibration. Combining with the output error model and misalignment angles of the inertial device, an attitude dynamic model and observation equations are established. The system’s observability is analyzed based on the theory of output sensitivity. According to the analysis, it is the low observability of the accelerometers' misalignment angles that mainly affects the calibration accuracy. Correlation coefficients are calculated with the estimation error covariance matrix in the Kalman filter, and the calculation results indicate that the low observability is caused by the linear correlations. A new scheme is proposed by establishing the platform coordinate system based on the input axis of one accelerometer, which can reduce the number of the misalignment angles and make all the error parameters observable. Simulation results show that the estimation error of the misalignment angles is less than 5" and the calibration accuracy is significantly improved by the improved scheme.

inertial platform; misalignment angle; observability; output sensitivity; correlation coefficient

V441

A

2015-06-03；

：2015-09-21

航天科技创新基金（CASC201105）

许永飞（1988—），男，博士研究生，主要研究方向为惯性导航。E-mail：xyf_xyf2008@126.com

联 系 人：张士峰（1971—），男，教授，博士生导师。E-mail：zhang_shifeng@hotmail.com

1005-6734(2015)05-0575-05

10.13695/j.cnki.12-1222/o3.2015.05.004