金融网络理论与应用综述

孙艳霞

（东北财经大学社会与行为跨学科研究中心，辽宁 大连 116025）

金融网络理论与应用综述

孙艳霞

（东北财经大学社会与行为跨学科研究中心，辽宁 大连 116025）

本文详细综述了金融网络理论在系统风险方面的应用。重点指出现实中的金融网络具有小世界网络和无标度网络的特征。对现实金融网络节点中心性的静态分析有助于寻找系统重要性银行，而网络结构变动的动态分析则包含预测金融危机和银行间市场利率的信息。

金融网络；理论与应用；系统风险

一、引言

随着金融创新的加快和银行间市场的不断发展，类似于CDS的金融衍生产品以及各种银行理财产品被不断设计出来，促使金融机构之间的资产负债关联日益紧密，整个金融系统呈现出越来越复杂的网络特征。金融机构是网络的节点，金融机构之间的资产负债关系则构成网络的边。银行间市场可被看成是一种金融网络，这一网络虽有利于流动性的分配，但也使得单个银行的风险通过网络连接传染至其他银行，发生多米诺骨牌效应，引致整个金融系统的崩溃。阿西莫格鲁等（Acemoglu等，2013）将金融网络内的这种级联反应称之为金融网络的外部性。

网络外部性可以解释与社会经济直接相关的内生变量无法解释的整体波动问题，比如股票市场的崩盘、群体事件等。因为社会经济活动是嵌入在社会网络之中的，经济主体的支付函数受到该主体所在的社会群体中其他成员的选择行为的影响（加布里埃利，2011）。由此，如果将金融体系看成金融网络，那么在看待金融风险问题时，除需关注“大而不能倒（Too-Big-to-Fail）”风险之外，还需注意“太关联而不能倒（Too-Connect-to-Fail）”风险（刘，2010）。在金融网络中，单个银行除受直接交易对手的风险行为影响之外，还会受到交易对手其他网络连接的间接影响。2008年的金融危机即是由次级贷款违约引发的风险传染事件，在这一过程中金融机构之间的关联性对系统风险的积累和扩散起到了重要的助推作用（贾彦东，2010）。危机过后“宏观审慎管理”成为主要国家的重要监管方向（周小川，2011）。“宏观审慎管理”思想的提出是以网络视角看待金融风险问题的体现。

金融网络理论通过网络节点和网络的边，可以直观地刻画出金融系统，有助于研究系统风险传染问题。目前利用金融网络建模研究金融系统性风险主要有三个方向：一是现实金融系统的复杂网络特征；二是何种网络结构最有利于金融系统稳定；三是基于实际数据构建网络对金融系统风险进行评估，并试图将多种传染渠道引入金融网络分析中。本文将从这三方面对相关研究进行综述。

二、真实金融网络结构及在其系统风险方面的应用

（一）现实金融系统的复杂网络特征

如其他领域的复杂网络一样，现实中的金融网络也具有小世界网络和无标度网络特征。

加布里埃利（2011）对欧洲银行隔夜拆借市场网络的研究发现，该网络非常稀疏，具有小世界网络特征且节点度的分布服从幂律分布，即大多数银行只与较少的银行交易，只有少数银行拥有较大的网络连接并且一般是大型银行。美国联邦基金市场网络与欧洲银行隔夜拆借市场网络结构类似，也具有小世界网络特征，但是网络节点度的分布并非是幂律分布，而是一种厚尾分布（贝克和阿塔莱，2010）。

除隔夜拆借市场外，澳大利亚月度银行间风险敞口网络的节点度分布服从指数为-1.87的幂律分布，整个网络的平均路径和聚集系数均比较小（博斯，2004）。美国支付结算系统网络也具有无标度网络特征。该网络较为稀疏，只有一些货币中心银行之间的连接较为紧密，其他银行与这些中心银行相连接，彼此之间的关联较少（索拉迈基等，2007）。此外，意大利银行同业存款市场网络（拉扎蒂和曼纳，2009）、欧洲CDS市场网络（佩尔托宁等，2014）、德国银行间市场网络（克雷格和冯·彼得，2014）、巴西银行与非银行金融机构网络（孔特等，2013）等均具有高度中心化且相对稀疏的网络特征，网络节点的度数具有异质性，大银行拥有较大的度数，处于网络的中心位置，节点的度较小的银行倾向于与节点的度较大的银行相连。

（二）金融网络结构特征的刻画在系统风险方面的应用

对真实金融网络结构的刻画有助于寻找系统重要性银行。例如，在复杂网络理论中，可以通过节点度中心性（Degree centrality）、介数中心性（Between centrality）、紧密中心性（Closeness centrality）和特征向量中心性（Eigenvector centrality）等网络拓扑结构来刻画一个节点在网络中的重要性（赫南等，2008）。以度数的中心性为例，在一个由N个节点构成的复杂网络中，一个节点的度为该节点与其他节点直接连接的边的数量，记为ki。度的中心性则是该节点的度占该节点所有可能连接边的总数的比例，即Ki/（N-1）（加布里埃利，2011）。可见，一个节点的度越大，该节点能够影响到的节点数量越多，因而该节点在整个网络中也就越重要。

可以通过计算金融网络中的各银行的网络中心性来确定系统重要性银行。通过该方法确定的系统重要性银行并非是资产规模最大的银行，而是在网络中处于关键位置的银行。加布里埃利（2011）对比了欧洲银行隔夜拆借市场中银行的网络中心性在金融危机前后的变化，发现2007年8月以后，中小银行的中心性提高，而大银行有所下降。这说明金融危机以后中小银行的系统重要性上升。

网络中心性不仅可以决定系统重要性银行，还对银行间市场利率具有预测作用。贝克和阿塔莱（2010）构建出了一个网络中心性指数，发现当借款银行的网络中心性指数高于出借银行的网络中心性指数时，借款银行可以获得一个较低的借款利率。相反，如果出借银行具有更高的网络中心性指数，则借款银行将获得一个较高的借款利率。塔巴克等（Tabak等，2014）利用2004年1月到2007年11月的巴西银行间市场相关数据发现银行间市场网络的聚集系数和银行间市场利率的变动负相关。

此外，对网络结构变动的动态分析还包含可以预测金融危机的信息。加布里埃利（2011）发现2007年8月金融危机发生以后欧洲货币市场网络呈现出明显的节点之间平均距离的缩短。塔巴克等（2014）指出无向网络的聚集系数和有向网络的入度的聚集系数越高，系统风险越大。米诺尤和雷耶斯（Minoiu和Reyes，2013）将1978年至2010年发生的几次银行危机作为时间点，利用184个国家的跨国银行数据构建网络，发现每次危机发生之前的银行网络连通性（Connectivity）都要高于危机发生之后的网络连通性。

综上，可以根据一年或多年的金融机构之间真实的资产负债关联数据，如银行间借贷数据、同业存款数据等构建金融网络，从静态和动态两个角度进行分析。首先可以从静态的角度，单独分析某个金融网络内的节点中心性以寻找系统重要性银行。其次从动态的角度，基于多年数据分别构建金融网络，考察网络结构的变动情况，从而为监管当局控制系统性风险提供参考。

三、网络结构与风险传染的关系

当把整个银行体系看成金融网络时，从组织脆弱性的角度可以看出不同网络结构对银行之间的风险传染的重要影响。最初关于网络结构与风险传染问题的讨论局限于一些简单的规则网络，如完全连接网络、环形网络，例如艾伦和盖尔（Allen和Gale，2000）。随着关于真实金融网络结构实证研究的增加，一些文献开始利用仿真技术研究随机网络、小世界网络和无标度网络与金融系统稳定性的关系，例如李守伟和何建敏（2012）、伦茨（Lenzu，2012）等。艾伦和盖尔（2000）最早研究了由4家银行构成的完全连接网络和环形网络的风险传染状况，发现完全连接网络内的风险传染程度要小于环形网络。这是因为在一个连接相对紧密的金融网络内，破产银行的损失可以被多家债权银行分担，从而降低负向冲击对每家银行的影响程度。

李守伟和何建敏（2012）的研究则认为小世界网络内的风险传染程度高于随机网络和无标度网络。完全连接网络内每个节点银行都与其他银行相连接，因而是连接最为紧密的网络。环形网络则是一个节点银行只与和自己相邻的两家银行连接，因而该网络十分稀疏。随机网络、小世界网络和无标度网络内并非每家银行都相互连接，但节点的连通性要高于环形网络，因而这三种网络的紧密程度介于完全连接网络和环形网络之中。那么究竟何种网络结构最有利于风险传染？是否紧密的网络要比非紧密网络更有利于风险传染？大量研究网络结构与风险传染的文献对此并未得出一致结论。

第一种观点认为网络边分布相对均匀的网络风险传染程度较小。该观点认为在一个相对紧密的网络内，由于一家银行与较多的银行相连接，当该银行破产时，其损失平摊到每个债权银行就相对较小，从而降低了破产银行对整个网络的冲击。艾伦和盖尔（2000）是该观点的提出者，随后弗雷克斯等（Freixas等，2000）发现相对完全连接网络，包含货币中心的层级网络更容易发生风险传染。米勒（Müller，2006）也证实均匀紧密网络比中心化稀疏网络更稳定。持有相同观点的还有克劳斯和詹桑特（Krause和Giansante，2012）。

第二种观点则认为紧密连接的网络比较容易发生风险传染。德格里斯和阮（Degryse和Nguyen，2007）通过研究比利时银行系统网络1993年至2002年间网络结构的变动发现，网络结构从早期的近似完全连接结构到以多家银行为货币中心结构的转变降低了传染风险发生的可能性和影响程度。利尔蒙特（Viver-Lirimont，2006）基于戴蒙德和迪布维格（Diamond和Dybvig）的模型，从理论上证明网络连通性越高，被传染的银行数量就越多，并且传染发生的速度越快。因而“不要把鸡蛋放进同一个篮子里”思想的分散化投资行为表面上看可以降低单个银行的风险，但是实际上这种分散化投资行为会增加银行之间的关联度，从而增加了传染风险。因而，从金融网络视角来看，分散化投资并非一定会降低银行的风险。布鲁斯科和卡斯蒂廖内西（Brusco和Castiglionesi，2007）的研究支持了利尔蒙特（2006）的观点，他们也认为银行之间互相持有资金会增加传染风险。

针对上述两种不同观点，还有一种观点认为网络结构与传染效应之间并非单调线性关系。例如，巴迪斯顿等（Battiston等，2012）认为第一种观点所谓的网络连接越紧密越不容易发生风险传染并不总成立。最优的银行间市场网络结构会随着冲击大小的变化而变化，具有中等水平连通性的网络最容易发生大规模的风险传染（拉德利，2013）。当负向冲击小于特定阈值时，均匀紧密的银行借贷网络更稳定。然而，当负向冲击大于特定阈值时，弱连接网络却比连接紧密的网络稳定（阿西莫格鲁等，2013）。鲍勤和孙艳霞（2014）基于中国银行业的资产负债表数据的仿真模拟也表明被传染银行数量与网络平均度①之间并非存在单调正相关的关系。

上述三种观点看似莫衷一是，甚至相互矛盾，实则并不冲突。造成网络结构与风险传染关系不统一的原因在于已有文献对网络结构的设定不统一。例如，第一种观点的研究通常是预先假设一种网络结构，然后人为分配各银行的银行间资产和负债，并且是平均分配给N家对手银行。如此设定的银行网络固然会起到平摊风险的作用，若是银行间资产和负债并非平均分配，则会得到不同的结论，如鲍勤和孙艳霞（2014）的研究。这说明网络结构对风险传染程度的影响，不仅要看网络连通性，还与网络边的粗细有关，即每条边所代表的银行间资产和负债在整个银行网络中的权重。此外，网络节点的大小也会对风险传染结果有影响，例如大银行破产与小银行破产引发的风险传染程度就会不同（克劳斯和詹桑特，2012）。因而对金融网络结构与风险传染关系的探讨，不能简单地预先假定一种网络结构，然后人为分配资金，而应结合经济现实，给予银行之间合理的相互交易的行为规则，通过银行间交易行为来分配资金，从而内生出网络结构。阿曼斯和格奥尔（Aymanns和Georg，2015）就试图从金融机构的行为入手内生金融网络。王等（Wang等，2012）则是基于内生金融网络思想将网络资本引入机构投资者行为分析中。

四、基于金融网络理论的系统风险实证研究

金融网络研究的一个重要方向即是利用真实数据对系统风险进行评估。若是可以获得银行之间一对一的资产负债数据，即可据此直接构建网络，考察一家或多家银行破产引发的风险传染问题，如米勒（2006）、德格里斯和阮（2007）、黄聪和贾彦东（2010）、索科洛夫（Sokolov，2012）等。然而，现实中银行之间一对一的资产负债数据较难获得，不过可以利用最大熵方法（厄珀，2011）估算银行间资产负债头寸。

（一）最大熵方法的应用与缺陷

最大熵方法是将金融网络表示成一个矩阵，然后估算矩阵中的非零元素。例如，一个由N家银行构成的金融网络，银行i流向银行j的资金可以用xij表示，银行j流向银行i的资金则用xji表示，则这N家银行构成的金融网络就可以表示成一个N*N矩阵：

在已知单个银行的银行间总资产和银行间总负债信息的前提下，可以利用最大熵方法求出矩阵X*中的非零元素，即为求解下式：

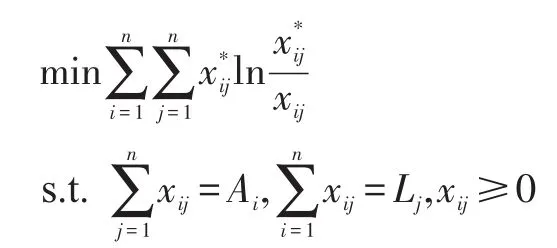
厄珀和沃尔姆（Upper和Worm，2004）根据德国各银行资产负债表中的银行间总资产和银行间总负债的数据，利用最大熵方法估算银行之间一对一的资产负债头寸，然后构建银行网络研究风险传染问题。他们发现，德国银行体系发生风险传染的概率尽管很小，但是一旦发生，仅通过银行间资产负债敞口就可以引发大规模的风险传染。该方法由于解决了数据可得性问题而得到广泛应用，例如米斯特鲁利（Mistrulli，2011）对意大利银行体系的研究、德格里斯和阮（2007）对比利时银行体系的研究、马君潞等（2007）对中国银行体系的研究等。

通过对最大熵方法的描述可以看出，最大熵方法实际上是假设金融网络为完全连接网络，即每家银行都与其他银行交易，这显然与真实银行网络结构不符。米斯特鲁利（2011）通过对比真实数据构建的网络和基于最大熵方法估算数据构建的网络，发现最大熵方法建立的网络会高估风险传染的程度。因而，基于最大熵方法构建的金融网络模型无法对系统风险进行准确评估，只能是一种参考。在具体应用时可以对该方法进行改进，例如，预先假设一种更贴近现实的网络结构，然后在最大熵方法的求解过程中添加约束条件（鲍勤和孙艳霞，2014）。

（二）传染过程的设定

利用金融网络建模评估系统风险的文献在传染过程的设定上，主要考虑银行间风险敞口引发的风险传染。这些文献通常假定一家银行或多家银行同时破产，这将导致这些银行的债权银行的银行间资产发生损失，若这一损失超过债权银行的资本金，则债权银行破产，从而发生多米诺骨牌效应（厄珀，2011）。在现实中，风险传染过程十分复杂，不仅银行之间债务的违约会令银行破产，危机时期债权银行提前收回对债务银行贷款的行为也会导致债务银行陷入流动性危机，部分银行甚至不得不折价抛售资产。此外，银行系统面临的共同冲击也会通过消耗单个银行的资本金而降低整个银行系统的稳定性，比如宏观经济的波动、房价下跌导致房地产贷款违约的增加等。因而有少量研究试图将流动性冲击、共同冲击与银行间风险敞口相结合，利用金融网络模型全面评估系统风险。

1.银行间风险敞口。银行间风险敞口是指银行在同业业务中产生的面临一定风险的同业资产。伴随着同业业务的不断发展，银行间风险敞口不断增加，银行之间的资产负债关联也愈发紧密，银行间风险敞口逐渐成为系统性风险的重要传染渠道。克劳斯等（2012）构建一个包含银行借贷网络的数理模型，从理论上论证了银行间风险敞口对系统性风险传染的重要影响。梅默尔等（Memmel等，2013）对德国银行体系、马丁内斯-哈拉米约等（Martínez-Jaramillo等，2014）对墨西哥银行系统等基于金融网络模型的实证研究也说明一家银行的破产仅通过银行间风险敞口这一单一传染渠道即可引致数家银行破产。

银行间风险敞口传染的过程可以由图1表示。在被传染之前银行i的资产负债表如图1所示，当银行i的债务银行k破产时，银行i的银行间资产xik发生损失，假设损失为LGDkxik（LGDk为银行k的违约损失率）。此时银行i需要用资本金来弥补该损失，若是银行i的资本金不足以抵补这一损失，即LGDkxik＞Ei，则银行i破产（刘，2010）。于是，债务银行k的破产风险就通过其与银行i的银行间风险敞口xik传染至债权银行i。银行i的破产又会按照同样的方式传染至其他银行。

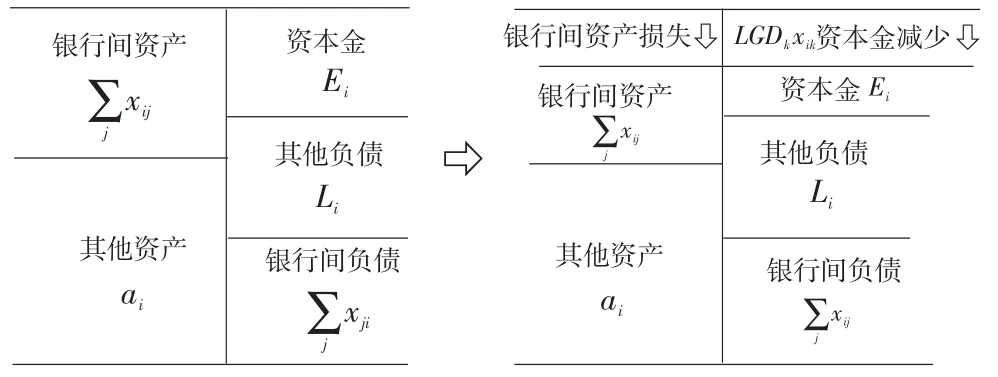
图1：银行间风险敞口引发风险传染原理

2.流动性冲击。埃斯皮诺萨-维佳和索伦（Espinosa-Vega和Solé，2011）在银行间风险敞口引发传染的基础上引入流动性冲击，其过程如图2所示。当危机发生时，假设银行i的债权银行h决定提前收回银行间资产xhi，若银行i没有足够的流动性储备，则银行i将不得不低价抛售其他资产。假设银行i的银行间负债中的αxhi部分需要通过抛售资产来偿还，由于抛售资产的价格下跌，银行i需要抛售多于αxhi单位的资产，即共需要抛售(1+ρ)αxhi单位资产，其中 ραxhi部分即是因资产价格变动而发生的资产损失，银行i需要资本金弥补这一损失，如图2右所示。结合图1中银行间资产违约的过程，如果，则银行i破产。

图2：流动性冲击下的银行资产负债表变动

3.共同冲击。尽管银行间风险敞口是系统风险传染的重要渠道，但是诸如汇率、利率等宏观经济变量波动构成的共同冲击对银行系统造成的损失要远大于金融网络内的传染损失（埃尔辛格等，2006）。格奥尔（2013）基于金融网络模型发现银行系统风险传染程度会随着共同冲击大小的增加而增加。国内学者郭晨和宋清华（2012）将国内生产总值、股票价格指数、房地产价格指数和一年期存贷款利差4个宏观经济变量作为银行系统的共同冲击，考察这些变量的波动对我国银行系统稳定性的影响。

这些文献说明共同冲击虽然不是风险传染的渠道，但却可以增加风险传染发生的可能性，并会通过消耗每家银行的资本金而降低整个银行系统的稳定性（班特和哈特曼，2000）。例如房价下跌造成房地产贷款违约的这一共同冲击会使得所有涉及房地产贷款的银行资产发生损失，从而损耗这些银行的资本金。

（三）违约损失率的影响

金融网络建模研究风险传染的一个重要假定即是破产银行对债权银行的银行间负债发生违约，致使债权银行的银行间资产发生损失。这一损失的大小与破产银行的违约损失率有关，违约损失率越大，债权银行的银行间资产损失就越大，风险传染程度就越严重。例如，马君潞等（2007）研究发现随着违约损失率的增加，被传染银行数量在不断上升。金融网络方向的文献大部分都外生假定违约损失率，每家银行被假定为具有相同的违约损失率，然后分别评估不同违约损失率下的风险传染情况。这种研究方法显然与现实相差甚远，因而少量文献试图尝试不同的方法来设定违约损失率。

梅默尔等（Memmel等，2012）假设金融网络内每家银行的违约损失率服从随机分布，然后基于此研究金融网络内的风险传染问题。该方法虽然考虑了差异化的违约损失率，但违约损失率仍是外生而非内生于经济。德格里斯等（Degryse等，2007）根据每家银行的资产负债情况构建了一个内生的违约损失率公式：

其中，θj为银行j的违约损失率，xij为银行i的银行间资产，LGDs为银行i除银行间资产之外的剩余资产的违约损失率。通过这一公式可以看出，该方法计算出来的违约损失率虽然结合了每个银行的资产负债情况，但也有诸多不妥之处，例如剩余资产的违约损失率仍需估算，初始破产银行的违约损失率仍然是外生的。

综上，基于金融网络模型对系统风险进行评估的实证研究面临诸多问题。首先是数据的可得性较差，基于最大熵方法估算的银行网络只是一种参考。其次，传染过程的设定仍然与现实相差较大。虽然部分文献考虑了流动性冲击和共同冲击，但是流动性冲击下的资产折价率、共同冲击对银行资本金的消耗程度以及违约损失率的设定等细节问题仍有待改进，不能简单地将这些参数假定为外生。

五、金融网络理论的总结与展望

2008年以雷曼兄弟破产为标志的金融危机说明现代金融系统不再是一个孤立的金融机构，而是相互连接的金融网络。单个金融机构的行为会对网络内其他金融机构产生重要影响，网络连接会助推系统风险的扩散。因而将金融机构视为网络的节点，将金融机构之间的资产负债关联视为网络的边来刻画金融系统，为我们研究金融问题尤其是系统风险问题提供了全新的视角。

首先，通过对真实金融网络结构的静态分析有助于寻找系统重要性银行，这一重要性银行并非一定是大银行。对网络结构变动的动态分析则蕴含着与预测金融危机有关的信息，从而为监管提供新的思路。其次，通过对网络结构与风险传染之间关系的探讨，有助于监管当局正确引导金融机构之间的交易行为。最后，利用金融网络来评估系统风险，可以作为CoVaR方法（肖璞等，2013）、压力测试法（曹麟和彭建刚，2014）等传统方法的补充。

尽管金融网络理论在探讨系统性风险方面有诸多好处，也有利于监管当局从宏观审慎管理的角度来看待系统性风险，但是该类研究也面临诸多困难。由于数据可得性较差，对真实网络结构的刻画并不全面，对系统风险的评估也只能是一种参考。未来利用金融网络评估系统风险时需要深入挖掘传染过程设定的诸多细节问题，如违约损失率的设定、流动性冲击和共同冲击中的参数设定等。此外，还可以将金融机构行为纳入金融网络分析中，一方面探讨金融机构行为对金融网络结构变动的影响；另一方面也可以探讨嵌入在金融网络中的金融机构的行为特征。

注：

①网络平均度指网络各节点度数的平均值。相对平均度低的网络，平均度大的网络更紧密。

[1]Acemoglu D，Ozdaglar A，Tahbaz-Salehi A.2013. Systemic Risk and Stability in Financial Networks[R].National Bureau of Economic Research.

[2]Gabrieli S.2011.The microstructure of the money market before and after the financial crisis：a network perspective[A].CEIS Tor Vergata Research Paper Series，9（1）.

[3]Chan-Lau J A.2010.Balance Sheet Network Analysis of Too-Connected-To-Fail Risk in Global and Domestic Banking Systems[J].IMF Working Papers.

[4]Bech M L，Atalay E.2010.The topology of the federal funds market[J].Physica A：Statistical Mechanics and its Applications，389（22）.

[5]Boss M，Elsinger H，Summer M，et al.2004.Network topology of the interbank market[J].Quantitative Finance，4（6）.

[6]Soramäki K，Bech M L，Arnold J，et al.2007.The topology of interbank payment flows[J].Physica A：Statistical Mechanics and its Applications，379（1）.

[7]Iazzetta，Carmela，and Michele Manna.2009.The topology of the interbank market：developments in Italy since 1990.Bank of Italy Temi di Discussione（Working Paper）No 711.

[8]Peltonen T A，Scheicher M，Vuillemey G.2014.The network structure of the CDS market and its determinants[J]. Journal of Financial Stability，13.

[9]Craig B，Von Peter G.2014.Interbank tiering and money center banks[J].Journal of Financial Intermediation，23（3）.

[10]Cont R，Moussa A，Santos E B.2013.Network structure and systemic risk in banking systems[J].Handbook of Systemic Risk

[11]Minoiu C，Reyes J A.2013.A network analysis of global banking：1978-2010[J].Journal of Financial Stability，9（2）.

[12]Allen F，Gale D.2000.Financial contagion[J]. Journal of political economy，108（1）.

[13]Lenzu S，Tedeschi G.2012.Systemic risk on different interbank network topologies[J].Physica A：Statistical Mechanics and its Applications，391（18）.

[14]Freixas X，Parigi B M，Rochet J C.2000.Systemic risk，interbank relations，and liquidity provision by the central bank[J].Journal of money，credit and banking.

[15]Müller J.2006.Interbank Credit Lines as a Channel of Contagion[J].Journal of Financial Services Research，29.

[16]DegryseH，NguyenG.2007.Interbankexposures：An empirical examination of contagion risk in the Belgian bankingsystem[J].InternationalJournalofCentralBanking，3（2）.

[17]Vivier-Lirimont，Sébastian.Contagion in interbank debt networks[R].Working Paper.February 2006，ReimsManagement School and CES，Paris I Pantheon Sorbonne University.

[18]Brusco S，Castiglionesi F.2007.Liquidity Coinsurance，Moral Hazard，and Financial Contagion[J].The Journal of Finance，（5）.

[19]Battiston S，Gatti D D，Gallegati M，etal.2012.Default cascades：When does risk diversification increase stability?[J].Journal of Financial Stability，（8）.

[20]Ladley D.2013.Contagion and risk-sharing on the inter-bank market[J].Journal of Economic Dynamics and Control，37（7）.

[21]Aymanns C，Georg C P.2015.Contagious synchronization and endogenous network formation in financial networks[J].Journal of Banking&Finance，50.

[22]Wang L，Wang S.2012.Endogenous networks in investment syndication[J].Journal of Corporate Finance，18（3）.

[23]Sokolov A，Webster R，Melatos A，et al.2012.Loan and nonloan flows in the Australian interbank network[J]. PhysicaA：StatisticalMechanicsanditsApplications，391（9）.

[24]Upper C.2011.Simulation methods to assess the danger of contagion in interbank markets[J].Journal of Financial Stability，7（3）.

[25]Upper C，Worms A.2004.Estimating bilateral exposures in the German interbank market：Is there a danger of contagion?[J].European Economic Review，48（4）.

[26]Krause A，Giansante S.2012.Interbank Lending and the Spread of Bank Failures：A Network Model of Systemic Risk[J].Journal of Economic Behavior&Organization，83（3）.

[27]Memmel C，Sachs A.2013.Contagion in the Interbank Market and its Determinants[J].Journal of Financial Stability，9（1）.

[28]Espinosa-Vega M A，Solé J.2011.Cross-border financial surveillance：a network perspective[J].Journal of Financial Economic Policy，3（3）.

[29]Elsinger H，Lehar A，Summer M.2006.Risk assessment for banking systems[J].Management science，52（9）.

[30]Georg C P.2013.The Effect of the Interbank Network Structure on Contagion and Common Shocks[J].Journal of Banking&Finance，37（7）.

[31]Bandt O，Hartman P.2000.Systemic risk A survey [R].European Central Bank.Working Paper，No.35.

[32]Memmel C，Sachs A，Stein I.2012.Contagion in the Interbank Market with Stochastic Loss Given Default [J].International Journal of Central Banking，8（3）.

[33]贾彦东.金融机构的系统重要性分析——金融网络中的系统风险衡量与成本分担[J].金融研究，2011（10）.

[34]周小川.金融政策对金融危机的响应——宏观审慎政策框架的形成背景，内在逻辑和主要内容[J].金融研究，2011，（1）.

[35]赫南，李德毅，淦文燕等.复杂网络中重要性节点发掘综述[J].计算机科学，2008，34（12）.

[36]李守伟，何建敏.不同网络结构下银行间传染风险研究[J].管理工程学报，2012，26（4）.

[37]鲍勤，孙艳霞.网络视角下的金融结构与金融风险传染[J].系统工程理论与实践，2014，34（9）.

[38]黄聪，贾彦东.金融网络视角下的宏观审慎管理——基于银行间支付结算数据的实证分析[J].金融研究，2010（4）.

[39]马君潞，范小云，曹元涛.中国银行间市场双边传染的风险估测及其系统性特征分析[J].经济研究，2007，（1）.

[40]郭晨，宋清华.宏观经济变量冲击与我国银行间市场风险传染[J].湖北经济学院学报，2010，8（3）.

[41]肖璞，刘轶，杨苏梅.相互关联性，风险溢出与系统重要性银行识别[J].金融研究，2013，（12）.

[42]曹麟，彭建刚.基于宏观压力测试方法的逆周期资本监管框架研究[J].国际金融研究，2014，（7）.

The Literature Review of Financial Network Theory and Application

Sun Yanxia

（Dongbei University of Finance and Economics，Dalian Liaoning 116025）

This paper reviews the application of financial network theory in systemic risk minutely.Financial network in reality has the characteristics of small world and scale-free network.A static analysis of financial network’s structure in the reality is helpful to find systemically important banks.Dynamic analysis of network structure includes the information that can predict financial crisis and interbank market interest rate.

financial network，theory and application，systemic risk

F832

A

1674-2265（2015）04-0028-07

（责任编辑 王 馨；校对 YJ，WX）

2015-3-15

孙艳霞，女，辽宁丹东人，东北财经大学社会与行为跨学科研究中心博士研究生，研究方向为金融工程、金融网络与仿真。