基于改进频域压缩感知的轴承复合故障欠定盲提取

周 俊，伍 星，迟毅林，潘 楠

(昆明理工大学 机电工程学院，昆明 650500)

由于机械结构的复杂性，传感器所测信号往往是故障源信号与其它噪声信号的混合体。因此，需抑制、消除干扰信号，保证能准确识别机械故障特征信号进行故障诊断［1］。因观测信号呈典型的非平稳性及高频调制特性，利用形态滤波可有效提高信号的边缘轮廓、形态特征及抑制背景噪声。现场测试时传感器个数有限，而机械故障源数目众多，加之复合故障存在，造成测试仅满足观测信号数目小于故障源数目的欠定条件。对此研究已引起关注，如沈路等［2］将形态滤波与灰色关联度方法相结合，实现轴承故障诊断，采用差值滤波器对故障信号进行滤波。郝如江等［3］将形态滤波与声发射结合用于轴承早期故障诊断。李豫川等［4］将形态滤波(MF)与传统稀疏分量分析(SCA)结合用于滚动轴承欠定盲分离。潘楠等［5］将频域SCA的欠定盲解卷积用于轴承声学诊断。余丰等［6］提出结合压缩感知(CS)与K均值奇异值分解(K-SVD)的稀疏分量分析方法对吉他声音进行欠定盲源分离。李丽娜等［7］基于势函数与压缩感知对钢琴声信号进行欠定盲源分离。

基于以上研究分析，本文提出多尺寸结构元素闭－开组合形态滤波器、遗传模拟退聚类及频域压缩感知重构算法相结合的滚动轴承故障欠定盲分离方法(C-OACMF-GASA-CS)。通过改进形态滤波(C-OACMF)滤除背景噪声;改进频域SCA算法，用遗传模拟退火的模糊C-均值聚类方法估计混合矩阵，利用频域压缩感知重构算法的正交匹配追踪(OMP)算法重构、估计轴承复合故障源信号，达到有效提取机械故障特征信息目的;通过仿真实际滚动轴承复合故障振动信号提取实验对该算法的有效性、准确性进行验证。

1 欠定盲分离数学模型

盲信号处理指在信号传输通道及源信号未知情况下仅据观测信号恢复估计源信号的技术。实际应用中观测信号数目小于源信号数目情况时有发生，盲源分离需在欠定条件下实现。而SCA为解决欠定盲源分离的常用方法。考虑噪声的SCA方法数学模型为

式中:X为观测矩阵，即传感器采集的实际信号值;A为混合矩阵，需通过算法求解;S为稀疏分布未知源信号;V为噪声或其它随机干扰成分;m为传感器拾取观测信号数目，n为未知源信号数目，m＜n;t为观测时间。

2 形态滤波

数学形态学用于故障特征提取方式主要构造形态滤波器提取振动信号中的冲击成份滤除背景噪声［8］。较传统滤波方法该算法简便、计算速度更快，易于硬件实现［9］。在一维信号处理中，数学形态学主要包括形态开、形态闭，定义为

式中:Θ，⊕分别为形态开、形态闭。

通常用形态开、形态闭的级联形式去除信号中正、负两种噪声。Maragos用同尺寸结构元素，定义形态闭－开、开－闭滤波器。

为抑制统计偏倚，常用形态开－闭(OC)及闭－开(CO)平均组合滤波器，即

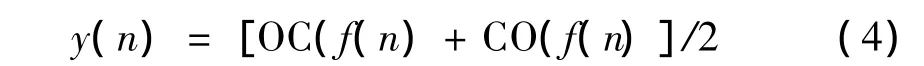
3 基于C-OACMF-GASA-CS的复合故障欠定盲提取

本文提出基于改进形态滤波器、遗传模拟退聚类与频域压缩感知重构算法实现轴承复合故障源欠定盲提取，基本流程见图1。

图1 基于C-OACMF-GASA-CS的流程图Fig.1 The flow chart of C-OACMF-GASA-CS

3.1 构建C-OACMF滤波器

形态滤波大多采用单一结构元素实现信号降噪，而同尺寸结构元素会使滤波器输出结果严重偏倚，因形态开－闭滤波器在开运算、消除正脉冲时会增强负脉冲噪声。同理，闭－开滤波器也不能滤除全部正脉冲噪声。为克服闭－开、开－闭滤波器不足，本文用不同尺寸、不同结构元素级联的闭－开组合形态滤波器(C-OACMF)。g1，g2分别为三角、半圆结构元素集，即

式中:Θ，⊕表示腐蚀、膨胀运算。

由于信号中不止一种噪声，采用多尺度不同结构元素对信号中多种信号滤波处理。常用结构元素有半圆型、十字型、直线型、三角型等。经验表明，半圆型结构元素能较好滤除随机噪声，三角型结构元素则对脉冲噪声滤波效果较好。故选三角型与半圆型结构元素。C-OACMF流程为:① 对观测信号x(t)进行均值化处理;② 计算观测信号局部极大、极小值，确定结构元素高度HL及长度KL集合;③ 将计算的HL，KL代入三角、半圆结构元素公式，构造结构元素集合 g1，g2;④ 将g1，g2代入式(5)、(6)的结果代入式(7)，获得y(n)组合滤波器集合C-OACMF;⑤ 用y(n)对观测信号x(t)滤波处理。由均值化处理后的观测信号中相邻峰值间隔最大、最小值确定结构元素长度，信号峰值最大、最小值确定高度范围。利用小(大)长度对应小(大)高度确定多尺度分析中结构元素，将结构元素尺寸代入半圆型、三角型结构公式，计算各自结构元素集合。

对采集的滚动轴承内圈故障分别用平均组合滤波器(MF)与C-OACMF滤波处理。C-OACMF分析时间较短，为0.259 s，而 MF 滤波时间为 0.587 s。由于 COACMF算法腐蚀膨胀运算次数是平均组合滤波器的一半，故在幅值上C-OACMF结果为平均组合滤波器的2倍。

3.2 遗传模拟退火(GASA)聚类算法

两步法为较常用的SCA方法。先估计混合矩阵A，再通过A估计源信号。估计混合矩阵常用聚类法。该方法属模糊C－均值聚类，但其在处理大规模数据时更易收敛到局部最优解。因此，本文将遗传算法、模拟退火算法与模糊C－均值结合形成一种混合聚类方法，可以有效克服收敛到局部最优解情况。基于遗传模拟退火算法的模糊C－均值聚类流程［10］为:

(1)初始化控制参数:种群个体大小sizepop，最大进化次数maxgen，交叉概率Pc，变异概率Pm，退火初始温度T0，温度冷却系数k，终止温度Tend。

(2)随机初始化c个聚类中心，并生成初始化种群Chrom，计算各样本隶属度及每个体适应度值fi(i=1，2，… ，sizepop)，即

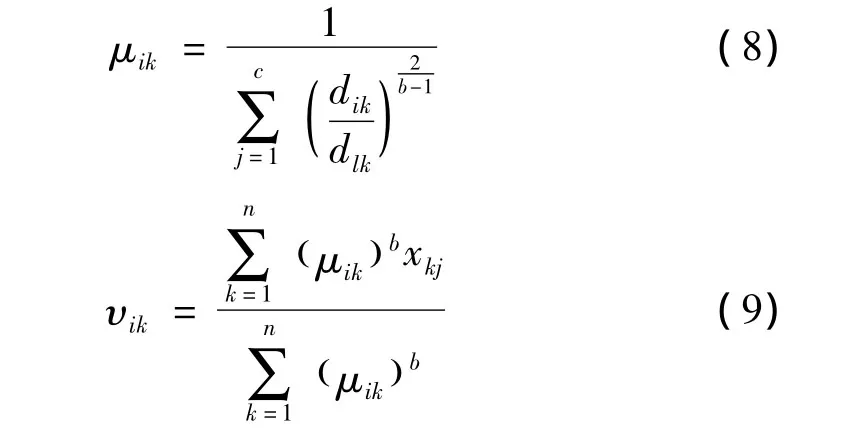
(3)设循环计数变量gen=0。

(4)对群体Chrom实施选择、交叉及变异等遗传操作，对新生个体用式(8)、(9)计算聚类中心、各样本隶属度及每个体适应度值fi'。若fi'＞fi，则以新个体替换旧个体;否则以概率P=exp((fi－fi')T)接受新个体，舍弃旧个体。

(5)若 gen＜maxgen，则 gen=gen+1，转至步骤(4);否则，转至步骤(6)。

(6)若Ti＜Tend，则算法成功结束，返回全局最优解;否则执行降温操作Ti+1=kTi，转至步骤(3)。

传感矩阵由混合矩阵转置矩阵构建，估计的混合矩阵转置矩阵分别为

3.3 压缩感知(CS)重构算法

信号稀疏性、传感矩阵设计、信号重构为压缩感知理论的基本组成部分。信号稀疏性体现信号本身或在某个基下能量集中程度，常用稀疏度度量［11］。信号重构速度、精度及信号稀疏度有密切联系，信号稀疏为压缩感知应用前提。本文通过快速傅里叶变换(FFT)将信号转换到频域，使其满足稀疏性要求。

建立压缩感知与欠定盲源分离等价关系，用OMP算法重构源信号。由于欠定性，m＜n，此为用压缩感知模型解决欠定盲源分离的先决条件。对压缩感知模型，构建一维混合信号。m个长度为t的观测信号可变换为 y=(y11，y12，…，y1t，…，ym1，ym2，…，ymt)T。

利用遗传模拟退火聚类算法获得估计矩阵的转置矩阵A(m×n)构建传感矩阵W。由压缩感知模型知，当混合信号y=(mt×1)时传感矩阵 W=(mt×nt)。利用傅里叶变换正交矩阵Et×t扩充矩阵A中元素:Bij=Et×tAij，其中Et×t的维数由信号长度 t决定，Aij为矩阵A(m ×n)元素值，Bij为 W=(mt×nt)的块矩阵，维数可由Bij=Et×tAij获得。具体转换为

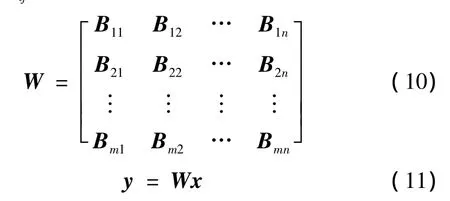
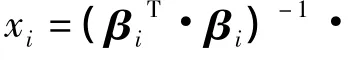
3.4 C-OACMF-GASA-CS算法总流程

该方法主要有:① 信号预处理，即形态滤波处理观测信号，提取轴承特征冲击信号并抑制噪声。滤波前，需据3.1节方法构建C-OACMF滤波器;② 估计混合矩阵，即用3.2节的遗传模拟退火算法模糊C－均值聚类算法求解混合矩阵;③ 重构源信号，即利用②的混合矩阵构建传感矩阵，据3.3节OMP算法在频域重构源信号;④ 故障识别，即对重构的源信号进行FFT变换，从而据分离信号幅值谱图中频率进行故障识别。

4 仿真

通过仿真信号验证C-OACMF-GASA-CS算法的有效性。仿真信号添加正负幅值为3的随机噪声信号，源信号1由单个冲击脉冲产生，间隔128点循环生成一个冲击脉冲，即

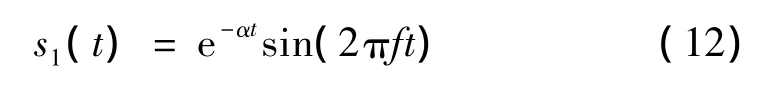
源信号2、3为正弦信号，产生公式为

源信号1冲击脉冲频率为100 Hz，源信号2、3正弦信号频率分别为45 Hz、10 Hz，幅值均为1。源信号1及噪声信号的信噪比为－6.8737 dB，源信号2、3与噪声信号信噪比均为－7.7722 dB。

仿真源信号时间波形及幅值谱见图2、图3。采样频率fs=1042 Hz，采样点数N=1042。混合矩阵为计算机随机产生的2×3维矩阵。添加噪声的3路源信号经混合矩阵后时间波形及幅值谱见图4、图5。由图4看出，3路源信号混合为2路，无法辨出;而图5的2个分量均存在2路正弦信号的45 Hz、10 Hz频率及微弱的冲击信号96 Hz频率，3路信号完全相互干扰混在一起。经C-OACMF-GASA-CS算法恢复所得分离信号时间波形、幅值谱见图6、图7。由二图看出，源信号均获得较好分离。图7(a)清晰显现出45 Hz谱线，符合源信号2的频率特征;图7(b)存在10 Hz谱线，符合源信号3的特征频率;图7(c)在96 Hz、104 Hz附近存在间隔8 Hz的边频谱线，符合源信号1的特征频率。因此，该算法能较好分离、恢复源信号。盲分离存在幅值、次序不确定性问题，使仿真源信号及分离信号幅值合次序存在差异，但不影响特征频率分析及算法有效性。

图2 源信号时间波形Fig.2 The time domain waveform of source signals

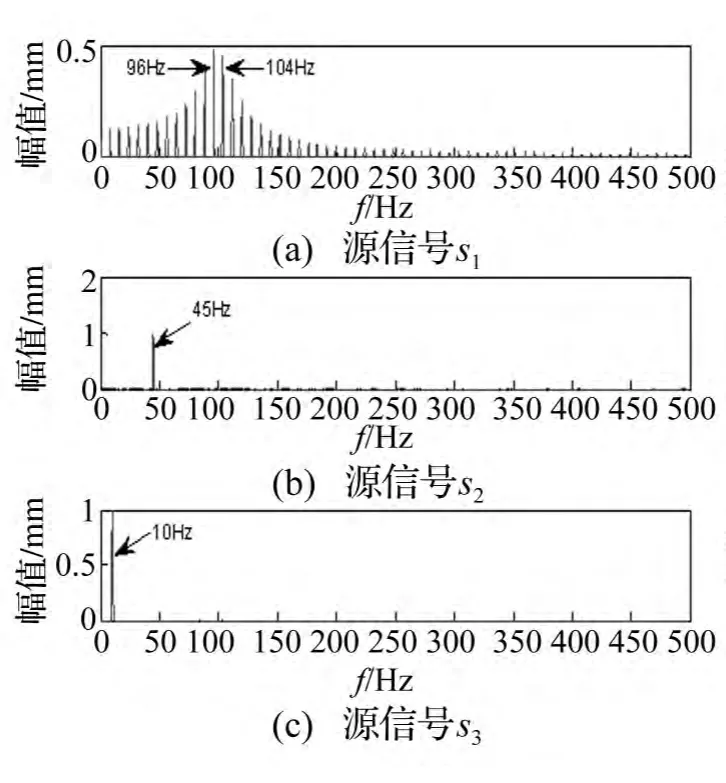
图3 源信号幅值谱Fig.3 The amplitude spectrum of source signals

图4 混合信号时间波形Fig.4 The time domain waveform of mixed signals

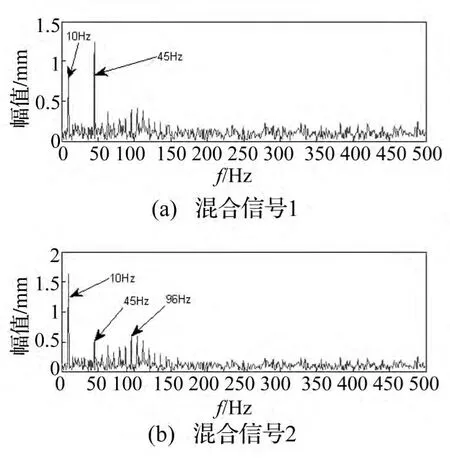
图5 混合信号幅值谱Fig.5 The amplitude spectrum of mixed signals

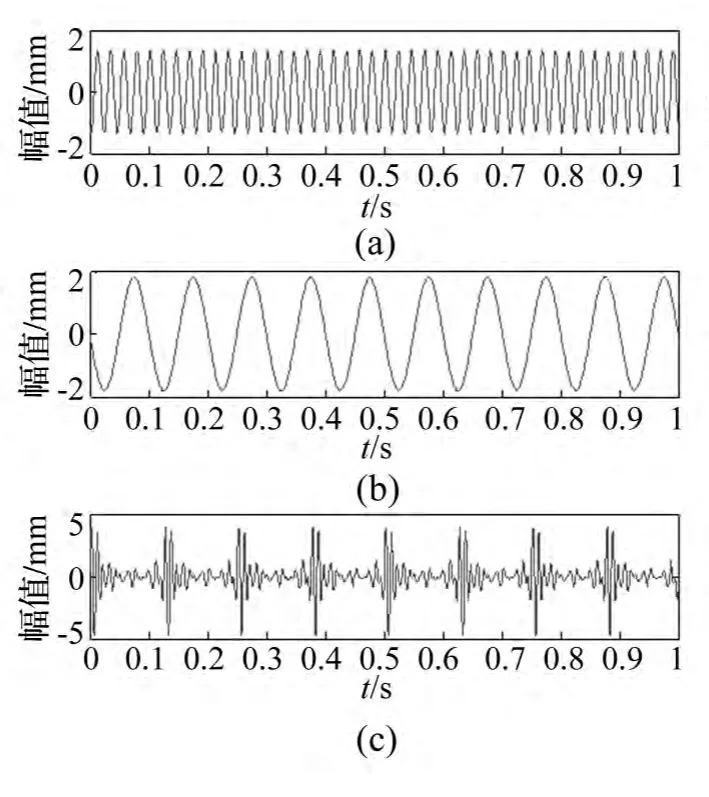
图6 分离信号时间波形Fig.6 The time domain waveform of separated signal

图7 分离信号幅值谱Fig.7 The amplitude spectrum of separated signal

5 实验

实际环境中存在大量背景噪声，通过对实测滚动轴承复合故障振动信号用频域MF-SCA算法、C-OACMF-GASA-CS算法实验分析，验证本文算法的有效性。利用QPZZ-Ⅱ旋转机械振动及故障模拟试验平台模拟滚动轴承故障。故障轴承节圆直径D=39 mm，滚动体直径d=7.5 mm，滚动体数目Z=12，接触角α=0。据此参数计算各特征故障频率。转速为800 r/min即转频 fr=13.33 Hz，内圈故障特征频率为 95.38 Hz，外圈故障特征频率为64.61 Hz，保持架故障特征频率为5.38 Hz。轴承故障形式为内外圈、保持架加工裂痕，内外圈裂痕约1 mm，保持架约0.5 mm。

利用NI SignalExpress采集模块及NI－9234四通道采集卡进行信号采集，采样频率fs=8192 Hz，采样点数N=8192。频率间隔 Δf=fs/N=1 Hz，将两对PCB加速度传感器相互垂直安装于轴承座上拾取信号。试验台及加速度传感器实物布置见图8。实验分析数据源于图8中传感器1、2，传感器安装于故障轴承座上。本次实验滚动轴承故障类型有内外圈复合故障、内外圈保持架复合故障。

图8 试验台及传声器布置图Fig.8 The test bench and microphone arrangement

5.1 轴承内外圈复合故障

轴承内外圈复合故障时域波形见图9，其Hilbert包络谱见图10。由图10看出，内外圈复合故障特征频率成分完全混在一起很难判断故障。观测信号经频域MF-SCA算法分离的复合故障信号频谱见图11。由图11看出，轴承内外圈故障基本分离，但存在大量边频及细小频谱线。

观测信号经改进形态滤波后包络谱见图12。经COACMF-GASA-CS分析结果见图13，可见2路信号均已成功分离，较图11、图12边频成份少，且不存在细小频谱线，分析结果简单明了。图13(a)中存在13 Hz、95 Hz及190 Hz的关键谱线，13 Hz为轴承转频，在95 Hz及190 Hz两侧存在间隔13 Hz的旋转频率边频成份，且190 Hz恰好是95 Hz的2倍频，结果符合计算的内圈故障频率95.38 Hz，对应内圈故障特征;图13(a)中清楚显示出65 Hz、130 Hz、195 Hz等谱线，结果符合计算的外圈故障频率(64.61 Hz)及倍频，对应轴承外圈故障特征频率;误差由频率分辨率导致(Δf=1 Hz)。

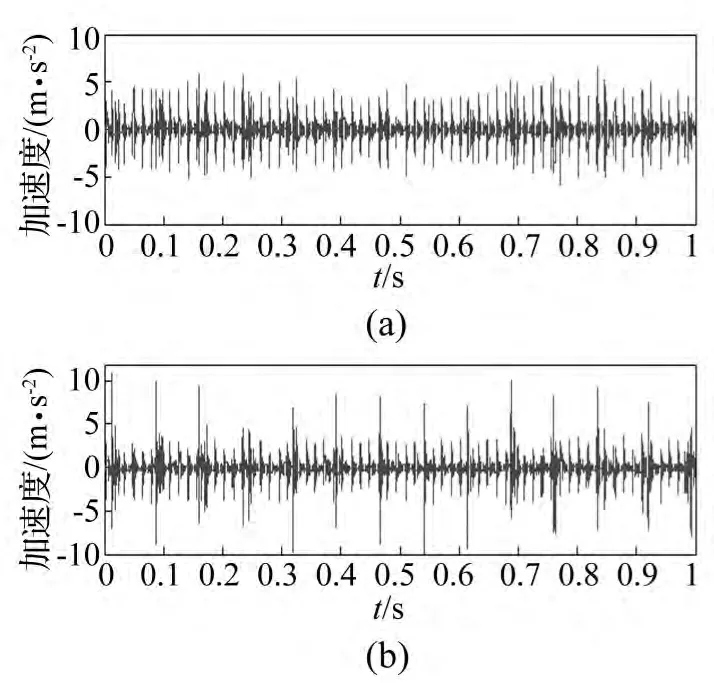
图9 内圈外圈复合故障时间波形Fig.9 The time domain waveform of mixed fault about inner ring and out ring

图10 内圈外圈复合故障包络谱Fig.10 The envelop spectrum of mixed fault about inner ringand out ring

图11 频域MF-SCA分离内外圈故障频谱Fig.11 The spectrum of mixed fault about inner ring and out ring separated by frequency-domain MF-SCA

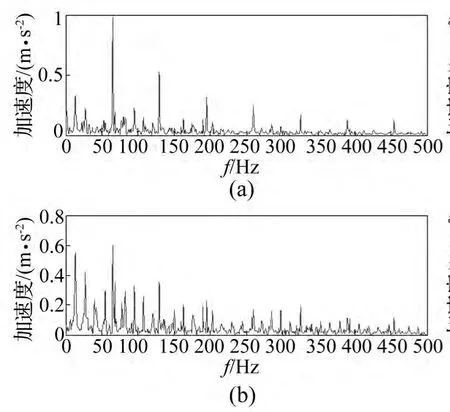
图12 C-OACMF滤波处理内外圈故障频谱Fig.12 The spectrum of mixed fault about inner ring and out ringfiltered by C-OACMF

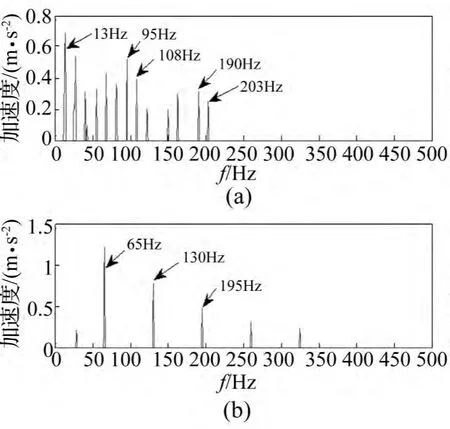
图13 C-OACMF-GASA-CS分离内外圈故障频谱Fig.13 The spectrum of mixed fault about inner ring and out ring separated by C-OACMF-GASA-CS

图14 内外圈保持架复合故障时间波形Fig.14 The time domain waveform of mixed fault about inner ring，out ring and cage

5.2 轴承内外圈保持架复合故障

双通道内外圈保持架复合故障信号时间波形见图14，包络谱见图15。由图15看出，频谱线杂乱无章，无法辨识故障。经频域MF-SCA算法分离的复合故障信号频谱见图16。由图16知，频域MF-SCA算法能分离内外圈故障，但对保持架微弱故障频率不能更好分离，存在微弱干扰信号。

观测信号经改进形态滤波处理的包络谱见图17。经C-OACMF-GASA-CS分析结果见图18，可见3路信号均已较好分离。与图16、图17相比，边频及细小谱线较少，结果较好，几乎不存在干扰成分。由图18(a)、(b)可清楚看到分离的内外圈故障，其判别方法与实验描述一致。对保持架微弱故障频率，图18(c)较好体现出1倍频5 Hz、2倍频10 Hz谱线。结果符合计算的保持架故障频率5.38 Hz，但仍存在未标注的13 Hz转频成分及倍频。

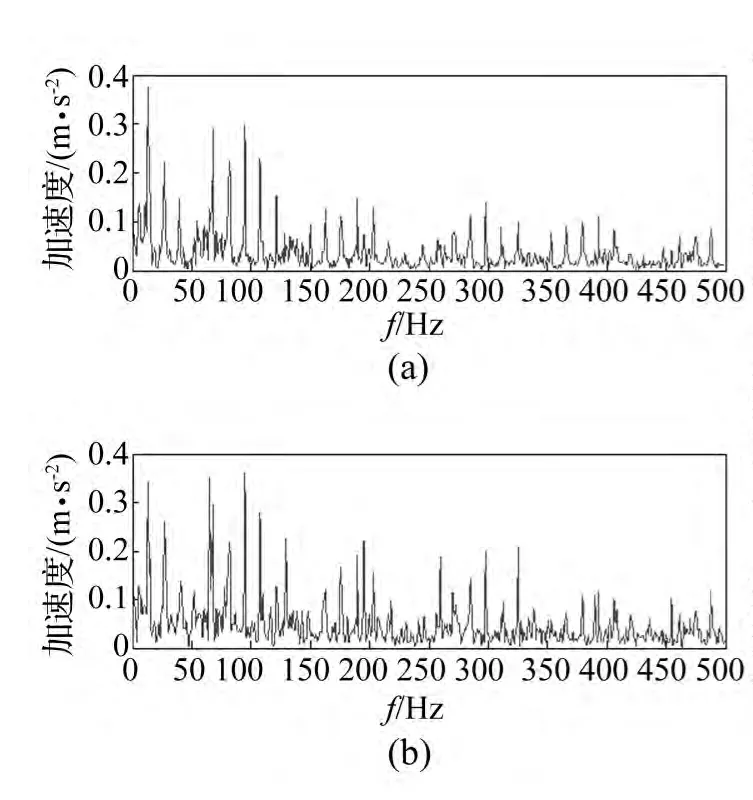
图15 内外圈保持架复合故障包络谱Fig.15 The envelop spectrum of mixed fault aboutinner ring，out ring and cage

图16 频域MF-SCA分离内外圈保持架复合故障频谱Fig.16 The spectrum of mixed fault about inner ring，out ring and cage separated by frequency-domainMF-SCA

图17 C-OACMF滤波处理内外圈保持架故障频谱Fig.17 The spectrum of mixed fault about inner ring，out ring and cage filtered byC-OACMF

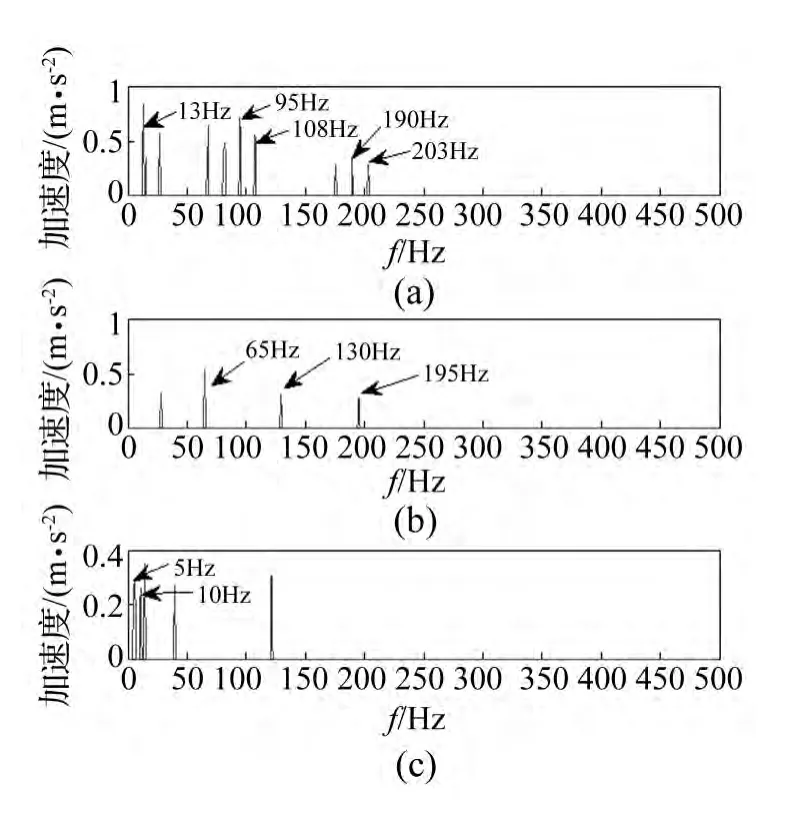
图18 C-OACMF-GASA-CS分离内外圈保持架复合故障频谱Fig.18 The spectrum of mixed fault about inner ring，out ring and cage separated by C-OACMF-GASA-CS

6 结论

针对复杂机械结构及工业环境中故障信号常被多种噪声掩盖情况，结合改进形态滤波、遗传模拟退火及频域压缩感知算法各自优点，提出新的轴承复合故障欠定盲分离方法。结论如下:

(1)该方法尤其对故障中微弱信号诊断简单有效。通过实验仿真及对实际采集的双通道滚动轴承加速度振动信号进行完备及欠定盲分离验证该算法，较频域MF-SCA算法，该方法在较好分离滚动轴承故障特征频率、保留信号特征频率同时亦可较好抑制细小边频及干扰成份。

(2)该方法分析结果简单明了，与平均组合滤波相比，滤波时间更短。机械噪声振动的故障特征与振动信号类似，对噪声信号处理、分析可有效了解机械设备的运行状态，实现状态监测及诊断。

［1］何正嘉，陈进，王太勇，等.机械故障诊断理论及应用［M］.北京:高等教育出版社，2010.

［2］沈路，周晓军，张文斌，等.基于形态滤波与灰色关联度的滚动轴承故障诊断［J］.振动与冲击，2009，28(11):17－20.SHEN Lu，ZHOU Xiao-jun，ZHANG Wen-bin，et al.Fault diagnosis of rolling element bearing based on morphological filter and grey incidence［J］.Journal of Vibration and Shock，2009，28(11):17－20.

［3］郝如江，卢文秀，褚福磊.形态滤波在滚动轴承故障声发射信号处理中的应用［J］.清华大学学报:自然科学版，2008，48(5):812 －815.HAO Ru-jiang，LU Wen-xiu，CHU Fu-lei.Morphology filters for analyzing roller bearing faultusing acoustic emission signal processing［J］.Journal of Tsinghua University:Science and Technology，2008，48(5):812 －815.

［4］李豫川，伍星，迟毅林，等.基于形态滤波和稀疏分量分析的滚动轴承故障盲分离［J］.振动与冲击，2011，30(12):170－174.LI Yu-chuan，WU Xing，CHI Yi-lin，et al.Blind separation for rolling bearing faults based on morphological filtering and sparse component analysis［J］.Journal of Vibration and Shock，2011，30(12):170 －174.

［5］潘楠，伍星，迟毅林，等.欠定盲解卷积用于滚动轴承复合故障声学诊断［J］.振动、测试与诊断，2013，33(2):284－289.PAN Nan，WU Xing，CHI Yi-lin，et al.Journal of Vibration，Measurement＆ Diagnosis，2013，33(2):284－289.

［6］余丰，奚吉，张力，等.基于CS与K-SVD的欠定盲源分离稀疏分量分析［J］.东南大学学报:自然科学版，2011，41(6):1127－1131.YU Feng，XI Ji，ZHANG Li，et al.Sparse presentation of underdetermined blind source separation based on compressed sensing and K-SVD ［J］.Journal of Southeast University:Natural Science Edition，2011，41(6):1127－1131.

［7］李丽娜，曾庆勋，甘晓晔，等.基于势函数与压缩感知的欠定盲源分离［J］.计算机应用，2014，34(3):658 －662.LI Li-na，ZENG Qing-xun，GAN Xiao-ye，et al.Under-determined blind source separation based on potential function and compressive sensing［J］.Journal of Computer Applications，2014，34(3):658 －662.

［8］孙敬敬.数学形态学在振动信号处理中的应用研究［D］.北京:华北电力大学，2012.

［9］沈路.数学形态学在机械故障诊断中的应用［D］.浙江:浙江大学，2010.

［10］史峰，王辉，郁磊，等.Matlab智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2011.

［11］刘冰.压缩感知框架下信号检测与参数估计算法研究［D］.哈尔滨:哈尔滨工业大学，2012.