基于KPCA降维的运动捕捉数据自动分割

陈思喜， 李建微， 陈 纾

(福州大学物理与信息工程学院， 福建 福州 350116)

基于KPCA降维的运动捕捉数据自动分割

陈思喜， 李建微， 陈 纾

(福州大学物理与信息工程学院， 福建 福州 350116)

针对运动捕捉获得的数据其维度通常较高， 在进行运动片段分割时候需要进行大量计算， 人工方法可以对运动捕获数据进行分割， 准确率比较高， 但是效率偏低的问题. 提出KPCA结合PPCA对捕获数据进行降维处理的方法， 将56维数据映射到2维空间； 以及构造特征函数获得投射误差的导数， 分析几何特征的变化， 探测运动捕捉数据的分割点的方法， 实现运动捕捉数据的自动分割.

运动捕捉数据; 降维； 自动分割； 泉州拍胸舞

0 引言

近年来， 运动捕捉技术在非物质文化遗产保护和传承方面应用很多. 运动捕捉技术是通过运动捕获设备记录人体运动信息以获取运动数据， 将运动数据与动画角色结合， 通过骨骼绑定， 还原成虚拟的动作实现非物质文化遗产的保护和传承. 冯晓宪等[1]应用动作捕捉技术对贵州少数民族民间舞蹈进行数字化研究; 邹虹等[2]在孔庙祀典方面深入探讨， 对舞蹈动作、 孔庙祀典活动的数据进行捕捉采集和三维虚拟重建. 民间舞蹈可以在捕获基本动作的基础上进行创意编排和设计， 以生成新的舞蹈动作， 就需要对捕获的基本动作进行运动分割. 人工方法可以对运动捕获数据进行分割， 准确率比较高， 但是效率很低.

自动分割技术应用广泛; 在运动捕捉数据的方面， 2004 年， Barbic等[3]提出了基于主成分分析PCA、 混合高斯模型GMM三种算法， 实现了运动捕获数据的分割， 并且取得较好的自动分割效果， 但是它们的算法运算效率较低. 2007年， Yamasaki 和 Aizawa[4]提出了基于改进形状分布的3D视频运动分割， 对运动视频自动分割的准确率达到92%， 但是该算法在高维非线性捕捉数据上的自动分割准确率不高. 2011年， 瞿师等[5]利用高斯过程隐变量模型实现数据的降维， 实现了基于隐空间的运动捕获数据自动分割， 在查准率和查全率方面获得成功， 但是该算法没有提及舞蹈动作的噪声分析. 2010年， Schulz和Woerner[6]用零交叉分割技术对人体运动捕捉数据进行分割， 该算法设置运动和休息两种状态， 对于运动幅度不大的捕捉数据的自动分割准确率较差. 本研究在前述文献的基础上改进算法， 采用核主成分KPCA结合概率主成分分析PPCA， 进行运动捕捉数据的特征提取降维， 并结合噪声分析， 核函数构造降维模型对项目组的泉州拍胸舞运动捕获数据进行自动分割. 达到简化计算量、 提高运算效率的目的.

1 数据映射

运动捕捉数据的维度通常较高， 在进行运动片段分割时候需要进行大量计算. 目前通常都是采用降维技术把高维数据降维后影射到低维空间， 然后进行数据分割.

主成分分析( principal component analysis， PCA)和核主成分分析(kernel principal component analysis， KPCA) 是常用的两种降维技术. PCA是一种线性方法， 但是人体运动过程中数据之间是非线性的并且有关联， 比如， 当左臀部移动左腿向前行走时， 有髋关节通常是倒退的， 因此在处理非线性问题时效果不是很好. KPCA使用核函数， 把非线性变换后的特征空间内积运算转换成原始空间的核函数计算， 计算量可以被简化， 提取出更好的属性之间的非线性关系. 常用的核函数主要包括以下几种[7]：

线性核函数：

多项式核函数：

高斯径向基核函数：

神经网络核函数：

由于动作捕捉数据是一个复杂的非线性过程， 并且考虑运动过程中数据的噪点， 经笔者实验分析， 本文采用核主成分KPCA进行运动捕捉数据的特征提取降维， 并结合概率主成分分析PPCA， 核函数构造降维模型如公式(5)所示.

其中：xi是yi对应的低维变量；xi∈RD；β、η为比例因子， 表示低维空间两个点的关联程度；γ表示高斯分布方差.

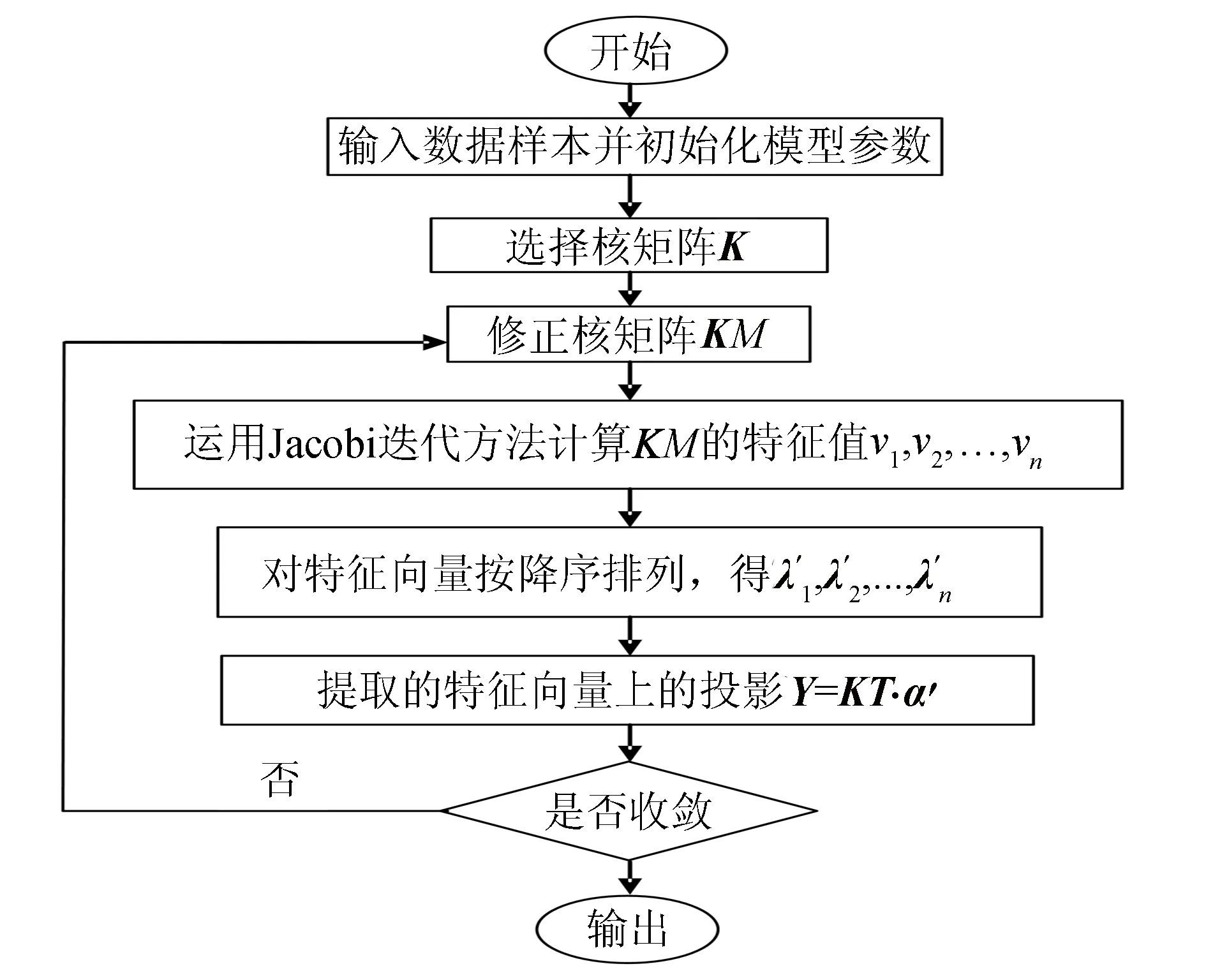
图1 KPCA-PPCA算法流程Fig.1 Flow chart of KPCA-PPCA

给定N个向量{xi}， 由公式(5)可得核矩阵K，K为N×N方阵. 其中

假设各分布均服从高斯分布， 对于每个分布的概率密度函数为：

其中：θ为模型的参数，

其中：x表示均值向量;C表示协方差矩阵;D为运动数据维数;Y为空间矩阵.

算法流程图如图1， 具体步骤如下：

1) 初始化模型参数：β=1、η=1、γ=1；

2) 计算核矩阵：

3) 修正核矩阵得到KM， 公式为：

4) 进行迭代， 求KM：v1,v2, … ,vn， 及对应的特征向量：λ1,λ2, …,λn；

6) 计算已修正的核矩阵K， 再提取出的特征向量上的投影Y=KT·α′， 其中α=(α1,α2, …,αt)；

7) 得到的投影Y即为数据经降维处理后的数据， 把序列n维数据降到t维.

2 自动分割

运动捕捉数据中， 不同运动序列的运动特征是不一样的， 所提取的特征向量也是不同， 并且表现出不同的几何特征. 通过降维技术， 把运动数据映射到低维空间， 经过奇异值分解(SVD)获得投射误差e， 比较投射误差比率Et， 根据Et的大小， 判断运动数据的分割点， 实现运动数据的自动分割.

以待分割的捕获数据Y为样本进行降维处理， 捕捉数据从D维空间映射到t维空间：

定义运动数据中心区域：

降维后近似帧为：

获得特征函数

将低维空间中的每一个xi分别代入特征函数， 计算运动捕获数据每一帧对应的运动特征函数值， 并转换为一系列离散值：

同时， 可以在t维空间内获得投射误差：

σ为运动数据在t维内经奇异值分解SVD后的奇异值.

Et投射误差比率， 它是一个指标， 表示经降维后在r维空间内保留多少信息.

利用Et的误差比率变化， 可以探测运动片段的分割点， 实现运动捕捉数据的自动分割， 具体分析如下：

1)t维空间内， 定义Et>τ，τ< 1，τ是一个经验常数， 经过实验，τ=0.75时， 能取得较好的效果；

2)在t维空间内， 定义一段长度为k的序列帧， 并满足Et>τ， 对于第i帧由公式(16)算出投射误差ei；

3) 对离散值求导， 得到di=ei-ei-l， 参数l必须足够大， 以保证噪声的干扰， 这里l=60;

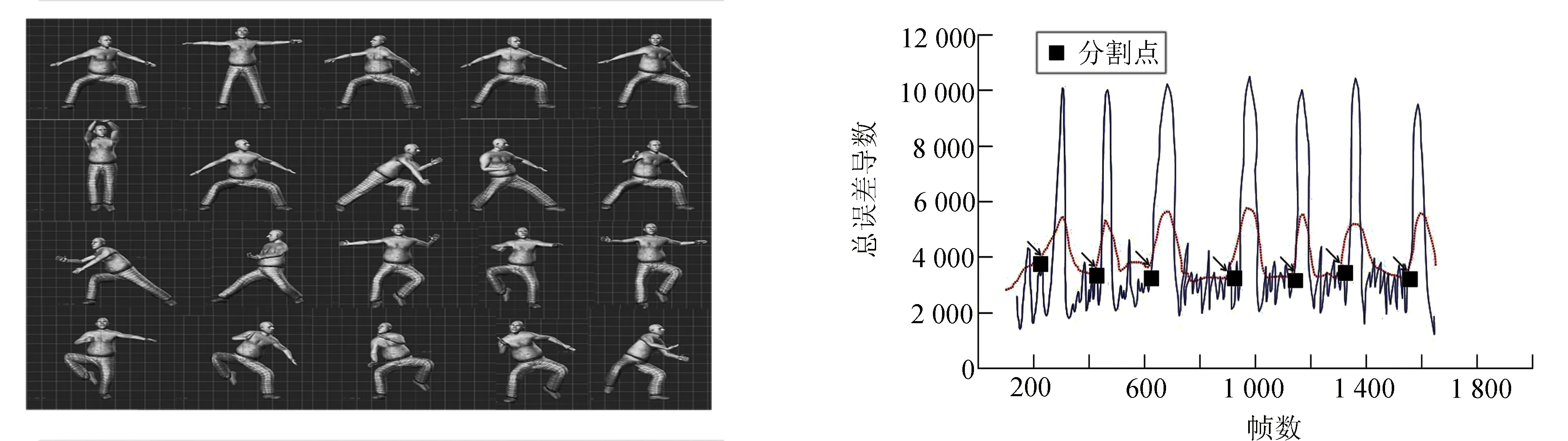
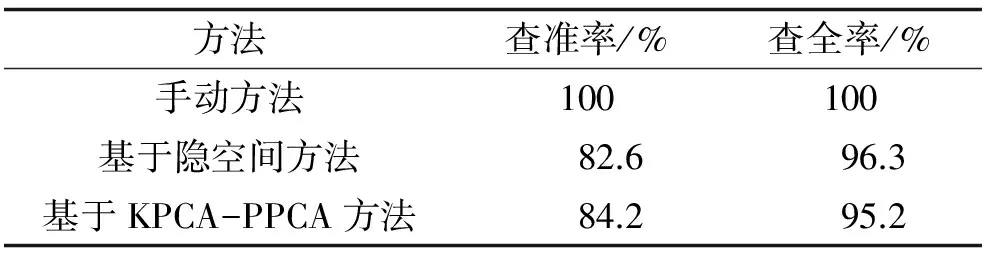
4) 初始值设定i=k， 对于相同的运动片段， dj的斜率是固定， 因为在t维空间特征函数值的导数没有发生变化； 当出现新的运动方式时候， dj(j

3 实验结果

实验采用数据来自福州大学课题组的项目“泉州拍胸舞动作捕捉数据库”， 拍胸舞是泉州的民间传统歌舞， 堪称闽南文化艺术的活化石， 是国家第一批非物质文化遗产， 广泛流传于福建南部沿海泉州各县区以及漳州、 厦门、 金门、 台湾等地区. “拍胸舞”基本动作为“打七响”： 包括双手胸前合击、 右手拍左胸、 左手拍右胸、 双臂内侧夹打左胁、 双臂内侧夹打右胁、 左手拍右腿部、 右手拍左腿部， 共得“七响”， 时值合七拍. 如图2所示. 定义人体关节有14个层次， 每个关节用一个4元数表示， 特征向量维度D=56， 降维后t=2. 选择待分割的泉州拍胸舞基本动作运动捕捉数据， 由7个运动片段组成， 共1 680帧. 图3是自动分割结果， dj随着运动动作的变化而产生的波动效果. 图中垂直方向表示1 682帧数据经算法检测后得到的导数， 黑色实线表示导数di， 点线表示导数的平均值， 黑色方块是表示运动方式发生的变化点， 也就是运动捕捉分割点.共探测出7个运动分割点. 分别位于252， 498， 685， 945， 1 171， 1 344和1 579帧.

图2 拍胸舞的基本动作图

表1 不同分割方法的性能比较

Tab.1 The performance of different segmen-tation methods

方法查准率/%查全率/%手动方法100100基于隐空间方法82．696．3基于KPCA-PPCA方法84．295．2

将7个运动片段分别用手动方法、 基于隐空间方法和基于KPCA-PPCA方法进行分割， 表1给出本文方法与其他方法的性能比较. 与手动分割的结果作比较， 参照瞿师等[5]人的性能指标， 用查准率和查全率来判断. 本文构造的算法结合噪声分析， 具有更高的查准率， 但是查全率稍低. 实验结果表明该算法结果具有一定可行性. 提出基于KPCA结合噪声分析的运动捕捉数据自动分割方法， 在降维处理中考虑噪声因素， 在特征函数中引入投射误差， 并通过求导来判断运动数据的分割点， 较好完成了运动捕捉数据的自动分割. 进一步研究算法， 提高降维的运算速率， 是下一步的研究内容.

[1] 冯晓宪， 舒瑜， 彭秀英. 贵州少数民族民间舞蹈数字化保护与开发研究[J]. 贵州社会科学, 2010, 243(3): 30-32.

[2] 邹虹， 李莹， 欧剑， 等. 基于动作捕捉技术的孔庙祀典数字化[J]. 计 算 机 系 统 应 用, 2012, 21(7): 151-154, 82.

[3] Barbic J， Safonova A， Pan J Y，etal．Segmenting motion capture data into distinct behaviors[C]//Proceeding of Graphics Interface Conference．London: Canadian Human-Computer Communications Society， 2004: 185-194.

[4]Yamasaki T, Aizawa K. Motion segmentation and retrieval for 3D video based on modified shape distribution[J]. EURASIP Journal on Advances in Signal Processing, 2007 (1): 211.

[5] 瞿师， 于荣欢， 吴玲达， 等. 基于隐空间的运动捕获数据自动分割[J]. 计算机应用研究, 2011, 28(8): 3 128-3 130.

[6]Schulz S， Woerner A. Automatic motion segmentation for human motion synthesis[C] // Proceeding of The 6th International Conference AMDO 2010. Mallorca: Lecture Notes in Computer Science, 2010: 182-191.

[7] 李洁. 基于核主成分降维的RBF网络降水预测[J]. 柳州师专学报, 2012, 27(1): 111-117.

(责任编辑： 林晓)

Automatic segmentation of motion capture data based on KPCA

CHEN Sixi， LI Jianwei， CHEN Shu

(College of Physics and Information Engineering, Fuzhou University, Fuzhou, Fujian 350116, China)

Motion capture data usually in high dimensions, which needs large amount of computation in motion clip segmentation. The accuracy of manual method is relatively high, but low efficient.In this paper, author carry out an automatic segmentate method by using Algorithm KPCA and PPCA to mapping 56 dimensional data into 2 dimensional Coordinate system,and constructing the feature function of projection error derivative to quantify geometric variables of data, and figure out the segmentate point.

motion caputure data; automatic segmentation; dimensionality reduction; Quanzhou chest-clapping dance

10.7631/issn.1000-2243.2015.04.0456

1000-2243(2015)04-0456-04

2013-12-03

陈思喜 (1975-)， 讲师， 主要从事数字媒体技术， 虚拟互动技术研究， sxchen@fzu.edu.cn

国家自然科学基金资助项目(31100415)； 福建省教育厅科技资助项目(JA10038)

TP37

A