LCL滤波的SAPF双环控制系统设计

苏忠钰， 齐 虹， 李锦彬, 2

(1. 福州大学电气工程与自动化学院， 福建 福州 350116; 2． 福建工程学院电子信息与电气工程系， 福建 福州 350118)

LCL滤波的SAPF双环控制系统设计

苏忠钰1， 齐 虹1， 李锦彬1, 2

(1. 福州大学电气工程与自动化学院， 福建 福州 350116; 2． 福建工程学院电子信息与电气工程系， 福建 福州 350118)

通过理论分析， 提出基于LCL滤波的并联型有源电力滤波器(SAPF)双环控制系统的设计方法. 结合具体实例, 从系统稳定性方面考虑， 提出LCL滤波器电网侧电感和逆变器侧电感的分配方式、 阻尼电阻和比例增益的选择方法. Matlab/Simulink仿真验证了所提参数设计方法的有效性.

电感分配； 无源阻尼； 比例增益； 重复控制

0 引言

近年来， 随着电力电子装置的广泛应用， 它所产生的谐波和无功功率给电网带来的危害日益严重， 很多电力用户原有的无源滤波器甚至无法使用， 这使人们的注意力投向有源电力滤波器(APF)[1].

为了滤除开关谐波， 通常采用L型或LC型滤波器. 传统的L型滤波器结构简单， 但在满足相同的高频滤波效果的情况下， 所需的电感值比LCL滤波器要大， 动态性能也变差[2]. LCL滤波器的滤波优势得以体现， 然而LCL型滤波器为三阶系统， 并且存在谐振点， 降低了系统的稳定性[3]. 为了提高系统的稳定性以及抑制LCL谐振, 通常需要加入阻尼作用, 包括有源阻尼和无源阻尼两种方式. 无源阻尼方式实现简单， 不受开关频率限制[4]. 因此， 采用无源阻尼方式提高系统的稳定性.

基于LCL滤波器的并联型APF， 多采用双闭环控制方式， 以保证系统的稳态精度. 现有的设计方案中， 参数的选取更多地依赖于经验值， 并且需要多次尝试才能找到合适的参数[5]. 大部分文献在参数设计时， 采用LCL滤波器参数与系统控制参数分别设计的方式. 本文通过分析LCL滤波参数， 尤其是电感参数对阻尼电阻以及比例控制参数选取的影响， 系统内环从稳定性方面考虑， 系统外环从稳态精度方面考虑， 提出了一种系统参数设计的方法. 理论分析和Simulink仿真验证了所提方法的正确性.

1 系统结构

基于LCL滤波器的并联型APF的主电路图如图1所示. 其中：us为网侧电压；Udc为直流母线电压；

L1为逆变器侧电感；L2为电网侧电感；C为滤波电容；Rd为阻尼电阻.

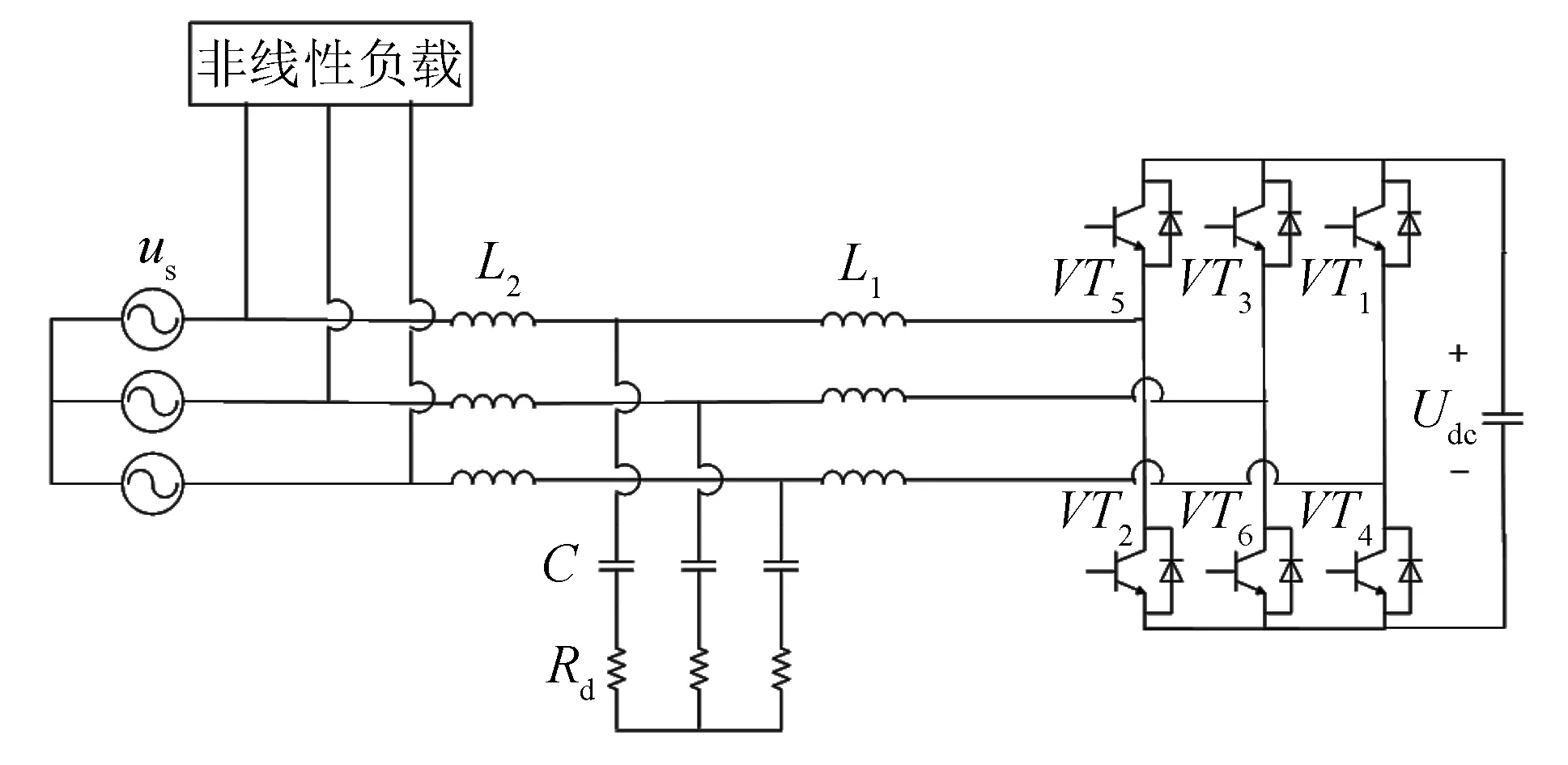
图1 并联型有源电力滤波器主电路图Fig.1 Main circuit diagram of SAPF

2 逆变器侧电感L1和电网侧电感L2的设计

设计实例为三相电网， 电压为380 V/50 Hz， 采样频率fs为10.2 kHz， 逆变器直流母线电压Udc为800 V， 非线性负载为三相整流桥， 带电阻RL=5 Ω与电感L=10 mH串联的阻感性负载.

根据低频段和高频段总电感量LT的要求[6]：

其中：Im为基波相电流峰值. 将Im=87 A，Udc=800 V,fs=10.2 kHz代入式(1)， 得867μH≤LT≤2 003 μH， 本实验取LT=1 600 μH.

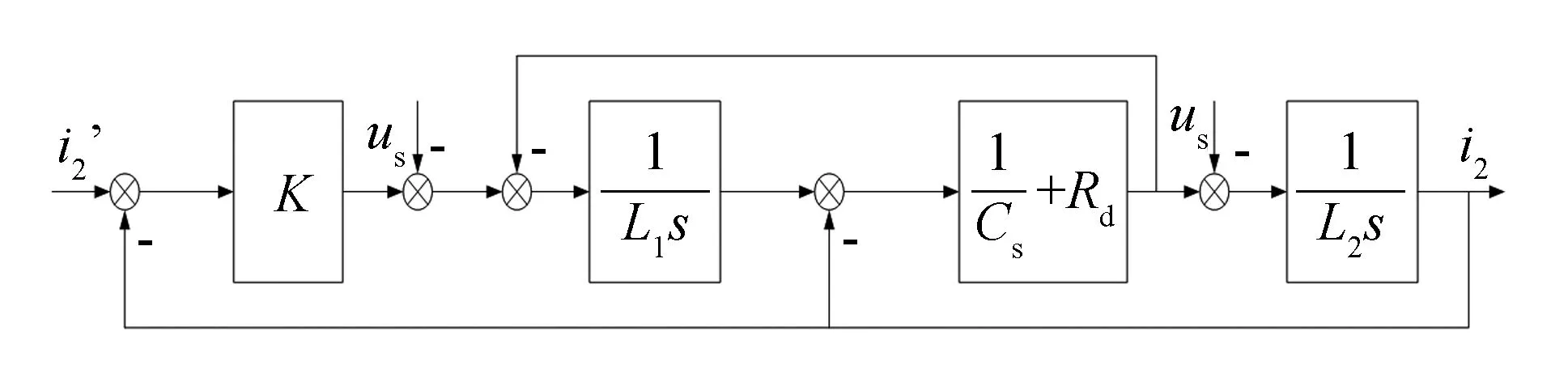
图2 内环控制结构框图Fig.2 Structure diagram of inner loop control system

在三相对称电路中， 可以只分析单相模型[7]. 由于交流系统的稳态误差不能够通过积分作用很好的消除， 并且积分作用还会带来相位滞后， 因此， 通过外环的重复控制来提高系统的稳态精度， 内环只需要采用简单的比例控制， 比例系数为K. 忽略直流母线电压波动、开关死区等因素影响， 当开关频率大于50 Hz， 且逆变器PWM工作在线性调制区时， 非线性控制系统可以近似等效为线性系统[8]. 由于PWM逆变器的开关频率相对较高， 为了简化分析， PWM逆变器用比例增益代替[9].脉宽调制方式采用SVPWM调制方式， 在此调制方式下逆变器的比例增益为1[10]. 电网电压被前馈入控制环， 使系统对电网电压的变化进行快速响应， 防止电网故障时电压突变引起输出电流过流[7]. 图2为系统内环控制结构框图.

由图2可求得， 内环的闭环传函为：

系统的特征方程为：

显然， 特征方程的各项系数均为正， 根据劳斯判据要使系统稳定必须满足：

在比例控制增益K， 电容C， 以及电感L1和L2确定的情况下， 可知：

为Rd的一元二次方程. 求解该方程可得：

由式(5)可知， 无论C，K，L1和L2为何值， 该一元二次方程都有一个正实根和一个负实根. 由于二次方程的抛物线开口向上， 并且Rd为非负， 因此， 要使系统稳定， 需要：

由式(6)可知， 当L1，L2之和为定值， 即系统总电感量LT设计好后，L1=L2时， 使内环闭环系统稳定的临界Rd值最大， 因此， 我们希望L1和L2相差较大， 使得所需阻尼电阻阻值不会太大， 以减小阻尼损耗.

由于阻尼电阻Rd不能太大， 且一般电容C比电感值小很多. 在阻尼电阻Rd， 电容C， 以及电感L1和L2确定的情况下，L1L2-CRd2(L1+L2)为正数， 由式(4)可得：

由式(7)可知， 当L1，L2之和为定值， 即系统总电感量LT设计好后，L1=L2时， 使内环闭环系统稳定的临界K值最小. 因此， 我们同样希望L1和L2相差较大， 使得比例增益的选取范围能够大一点.

通常逆变器侧电流纹波含量不希望过大， 过大纹波电流会增加功率模块的损耗与温升， 降低器件使用寿命， 而逆变器侧电感L1的大小决定了逆变器侧的纹波电流， 并且L1占总电感LT的50%～90%时， 随着L1的增大阻尼损耗先是减小而后是不增的趋势[6]. 再结合无论是从阻尼电阻Rd还是比例增益K使内环系统稳定的选取范围方面考虑， 都希望L1和L2相差较大. 因此， 逆变器侧电感取为比电网侧电感大得多， 取L1=1 400 μH,L2=200 μH.

3 滤波电容的选择

有源电力滤波器的单相等效电路如图3所示， 当Rd=0 Ω时， 从逆变器输出电压ui到电网侧电流i2的传递函数为：

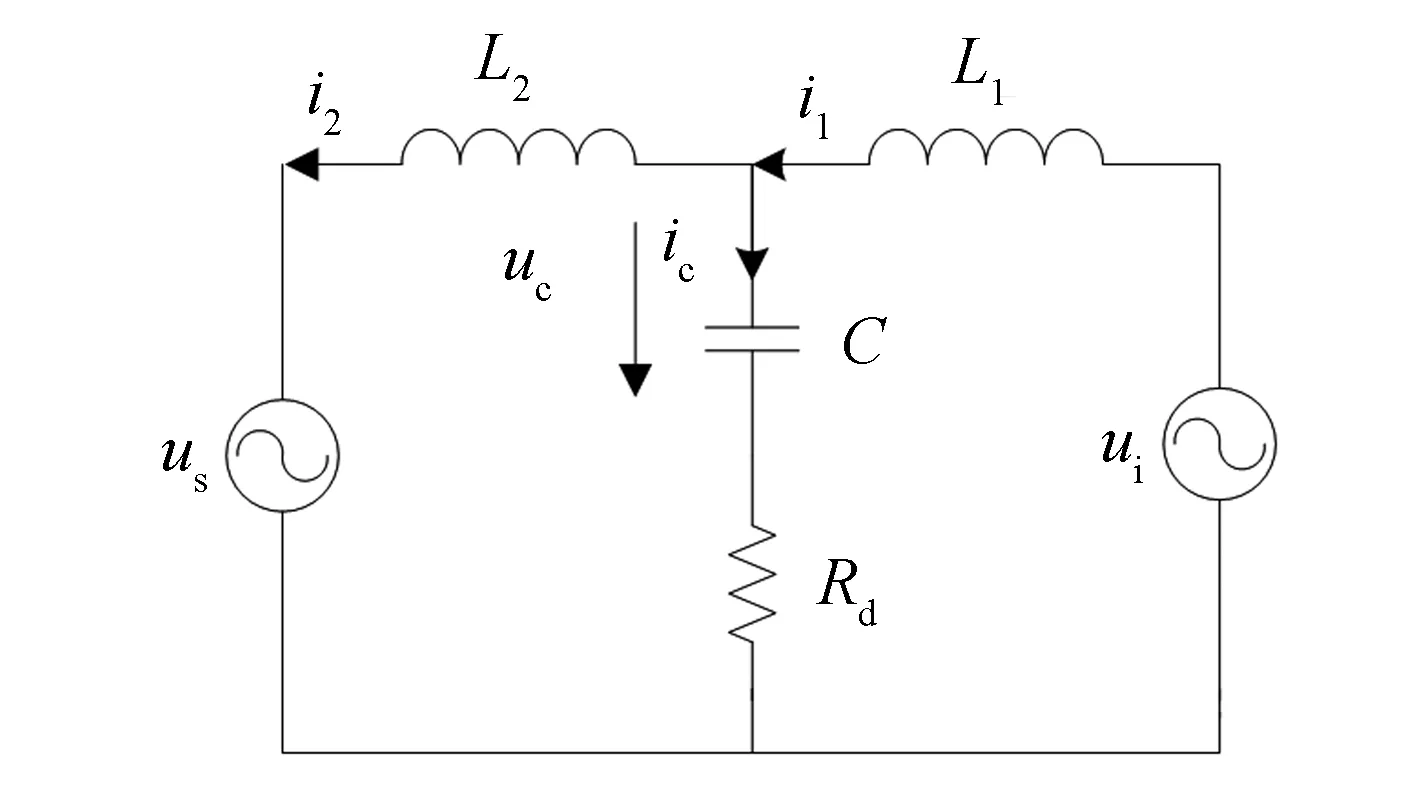
图3 并联型APF的单相等效电路 Fig.3 Equivalent circuit of SAPF in single phase

即LCL的电抗为：

将j2πfres代入式(9)， 令式(9)等于0， 舍去fres=0， 求得LCL的谐振频率为：

由式(10)求得：

工程上谐振频率一般在50ff～fs/2即[2.5， 5.1] kHz之间[6]. 其中：ff为基波频率， 即工频50 Hz；fs为采样频率. 式(11)代入L1和L2的值, 得到C取值范围为5.56～23.16 μF， 取滤波电容C=10 μF. 在fs=10.2 kHz 下，XC=1/(2πfsC)=1.56 Ω，XL1=2 πfsL1=89.7 Ω，XL2=2πfsL2=12.8 Ω，XL1和XL2比XC大得多， 保证了网侧和逆变器侧的高频分流通路[6].

4 阻尼电阻Rd和比例增益K的选取

由图2求出内环的开环传函：

不同阻尼电阻和不同比例增益下内环开环、 闭环对LCL谐振抑制能力的对比分别见表1和表2. 表中的数据为内环开环和闭环波特图幅频特性的极大值， 体现LCL谐振能否得到抑制.

由于LCL谐振处， 差不多就是内环系统波特图相频部分穿越-180°处， 即系统幅值裕度差不多为表中数据的相反数(幅值裕度略大一点)， 因此， 系统对LCL谐振的抑制能力还反映了系统的稳定性.

对比表1或者表2中内环开环和闭环对LCL谐振的抑制能力可知， SAPF的双闭环系统的稳定性与单闭环系统相比有所降低. 由于外环的重复控制主要起到改善系统稳态精度的作用[11]， 而内环闭环系统为整个SAPF外环系统开环的一部分， LCL在内环闭环的谐振很大程度上影响整个SAPF双闭环系统的稳定性. 因此， 不能通过内环开环波特图来设计阻尼电阻值Rd和比例增益值K. 而应根据内环闭环对LCL的谐振的抑制能力， 选取使双闭环系统稳定的阻尼电阻值Rd和比例增益值K. 工程上对幅值裕度的要求是6 dB， 因此， 综合考虑取K=3，Rd=1 Ω.

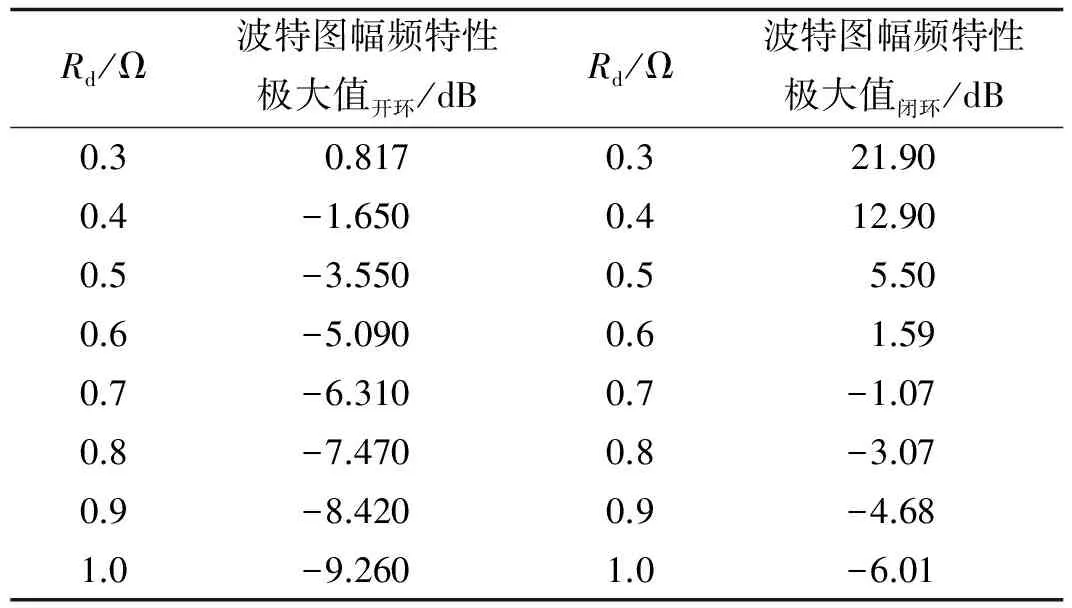
表1 K=3， 内环对LCL谐振的抑制能力

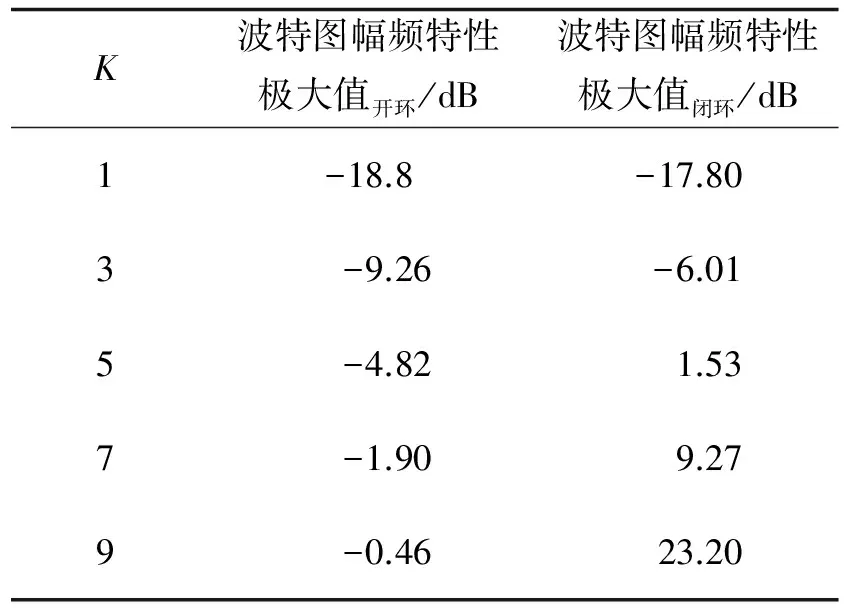
表2 Rd=1 Ω， 内环对LCL谐振的抑制能力

5 重复控制外环的设计

5.1 基于重复控制的双环结构

重复控制是基于内模原理的一种控制方法[12]. 得益于重复内膜对谐波信号提供的高增益， 重复控制适合于处理APF的谐波跟踪问题[11]. 因此， 为了提高系统的稳态精度， 外环采用重复控制， 基于重复控制的双环控制结构框图如图4所示. 图中：N=fs/f0，fs为采样频率，f0为基波频率[13]； M是衰减滤波器， 其值通常小于1[14]. 图5为内环闭环波特图的相频特性部分. 由于内环闭环传函存在相位滞后， 需要用超前环节zk校正， 取k=2. 电流指令除了输入给重复控制外环， 还送给内环进行前馈控制， 使系统可以对ir的变化进行快速响应[7].

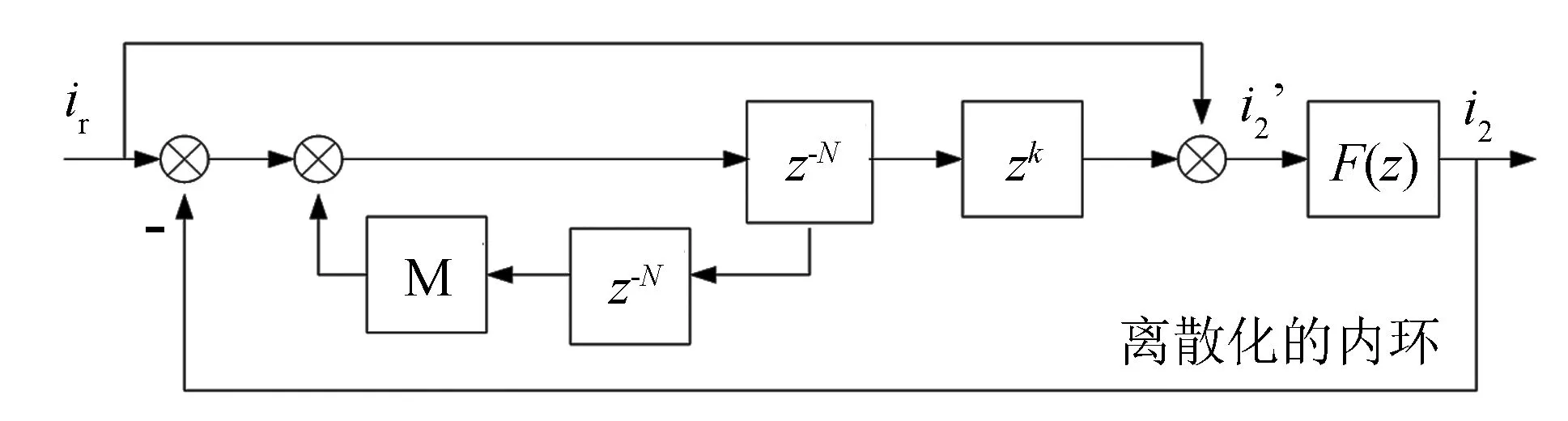
图4 外环为重复控制的双环控制结构框图Fig.4 Structure diagram of double-loop control system with repetitive control outer loop

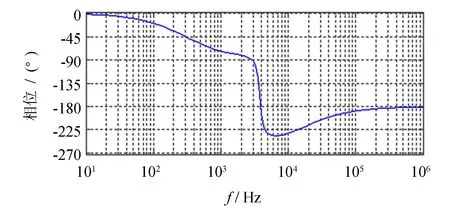
图5 内环闭环波特图Fig.5 Bode plot of the inner closed-loop

5.2 整个系统的稳定性

双线性变换不改变系统的稳定性. 因此， 利用双线性变换将内环离散化， 通过图4可得整个系统的闭环传函Φ(z)：

根据离散系统的稳定条件， 为了使双闭环系统稳定，zkF(z)+zN-M=0的根要在单位圆内. 由于N一般较大， 特征方程的根太多， 不便求解. 由小增益原理[15]得到整个双环系统稳定的充分而非必要条件为：

为自然指数

当L1=1 400 μH、L2=200 μH、C=10 μF时， 采样频率为10.2 kHz， 即N=204， 采样时间Ts=0.02/204 s， 代入F(z)分别画出不同阻尼电阻和不同比例增益下zkF(z)-M的模在复平面的轨迹如图6和图7所示， 其中衰减滤波器M值取工程经验值0.98[12]， 以保证稳定性. 图中实线为单位圆， 虚线为双环系统稳定性充分条件的轨迹.

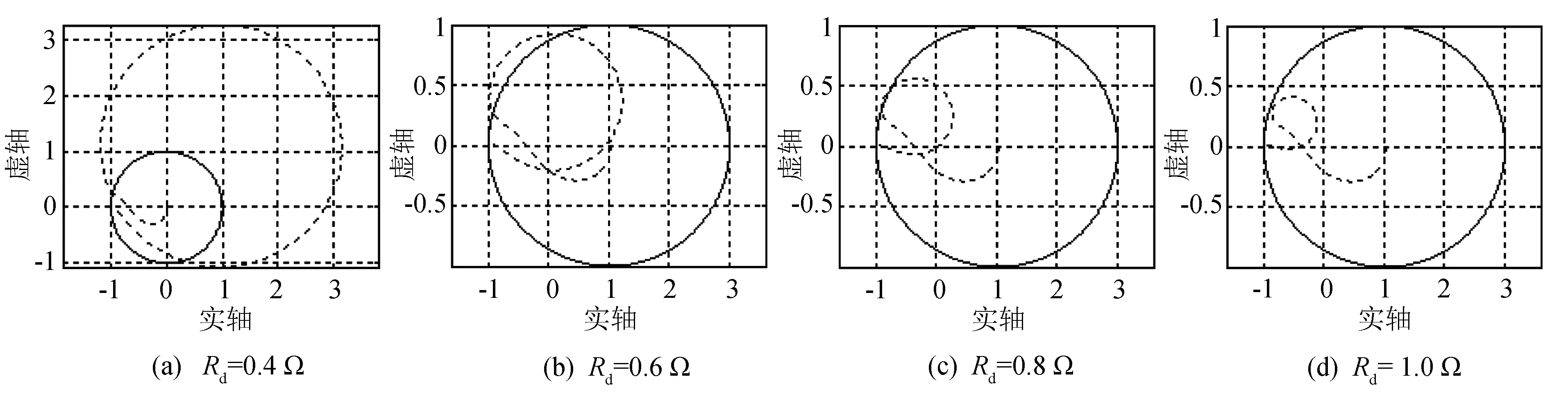
图6 比例增益K=3， 阻尼电阻Rd取不同值双环系统稳定充分条件的轨迹图Fig.6 Locus diagrams of sufficient condition for stability of double-loop control system with proportional gain K=3, damping resistor Rd takes different values

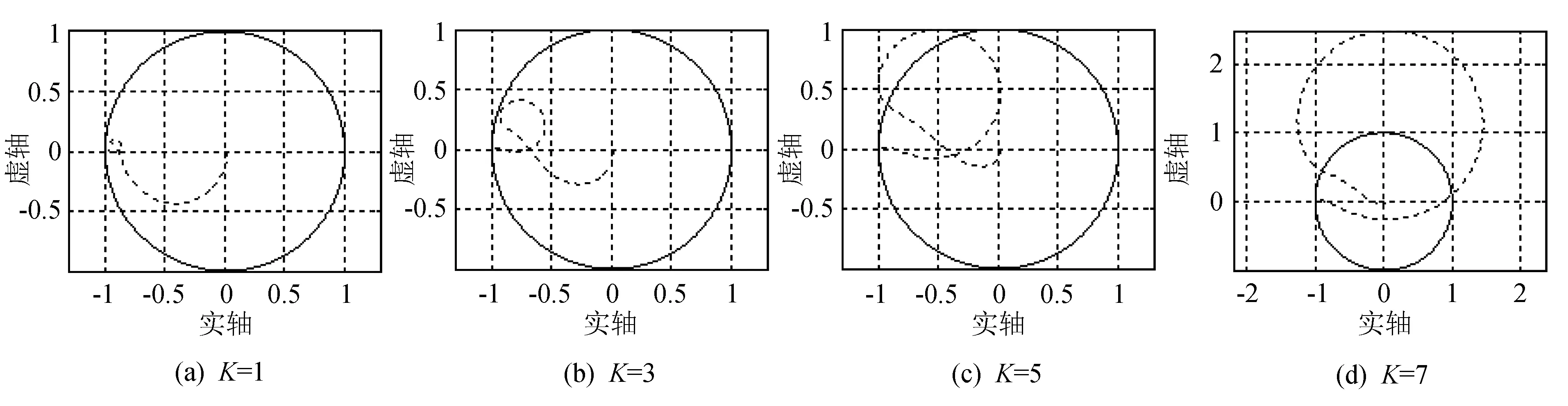
图7 阻尼电阻Rd=1 Ω， 比例增益K取不同值双环系统稳定充分条件的轨迹图Fig.7 Locus diagrams of sufficient condition for stability of double-loop control system with damping resistor Rd=1 Ω, proportional gain K takes different values

由图6和图7可知， 取K=3，Rd=1 Ω时， 双环控制系统是稳定的. 本设计实例中无需根据整个系统的稳定性对阻尼电阻和比例增益值进行修正. 说明根据内环闭环传函对LCL谐振抑制能力来选择阻尼电阻和比例增益值是可取的.

6 系统仿真

在Matlab/Simulink下搭建仿真电路对系统进行仿真. APF仿真模型中， 三相电网电压为380 V/50 Hz， 采样频率为10.2 kHz， 逆变器直流母线电压Udc为800 V， LCL滤波器设计的参数为：L1=1 400 μH，L2=200 μH，C=10 μF. 非线性负载为三相整流桥， 带电阻RL=5 Ω与电感L=10 mH串联的阻感性负载. 图8和图9分别为在不同阻尼电阻下和不同比例增益下APF的滤波效果. 图10和图11分别为Rd=1 Ω,K=1和K=3时， 系统补偿稳定后电网电流的谐波畸变率.

由图8可知， 当比例增益K=3， 阻尼电阻Rd小于0.7 Ω时， 系统不稳定， 阻尼电阻Rd=0.9 Ω开始， 双环控制系统才有较好的滤波效果. 由图9可知， 当阻尼电阻Rd=1 Ω， 比例增益K<3时， 双环控制系统才稳定. 由图10和图11可知， 比例增益K=1时， 双环系统补偿的电网电流总的谐波畸变率(THD)为1.2%， 比例增益K=3时， 双环系统补偿的电网电流 THD为0.41%， 系统的运行效果最好. 因此， 本设计实例无需根据仿真效果对阻尼电阻和比例增益值进行修正， 说明本设计方法的有效性.

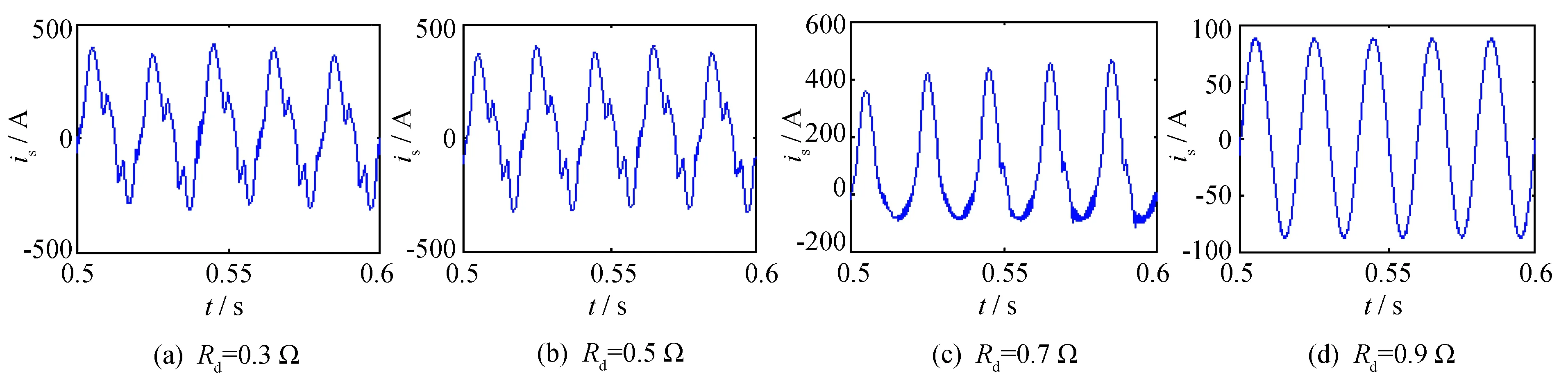
图8 比例增益K=3， 不同阻尼电阻下APF滤波效果Fig.8 Proportional gain K=3， filtering effect of APF when damping resistor Rd takes different values

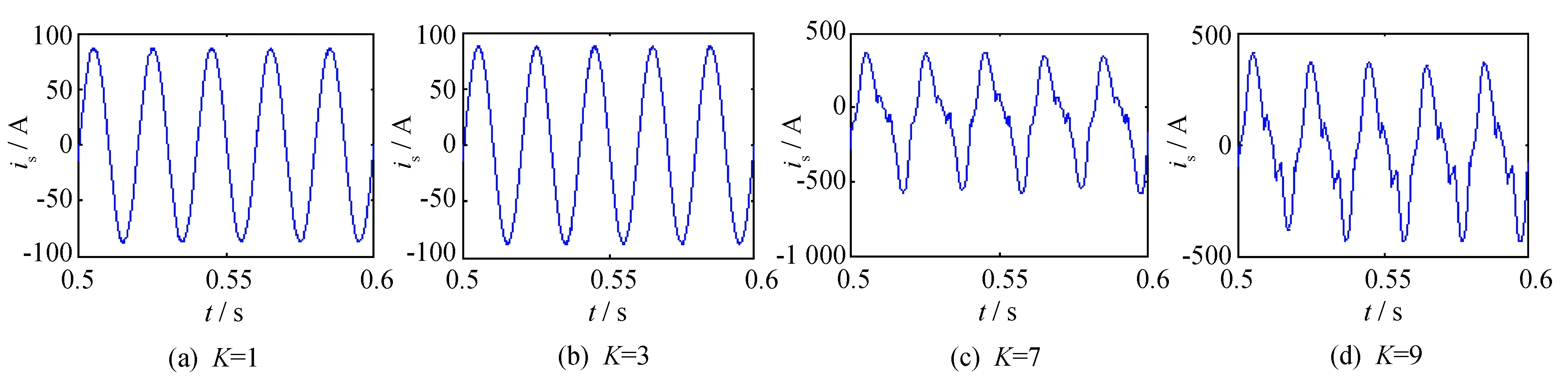
图9 阻尼电阻Rd=1 Ω， 不同比例增益下APF滤波效果Fig.9 Damping resistor Rd=1 Ω, filtering effect of APF when proportional gain K takes different values

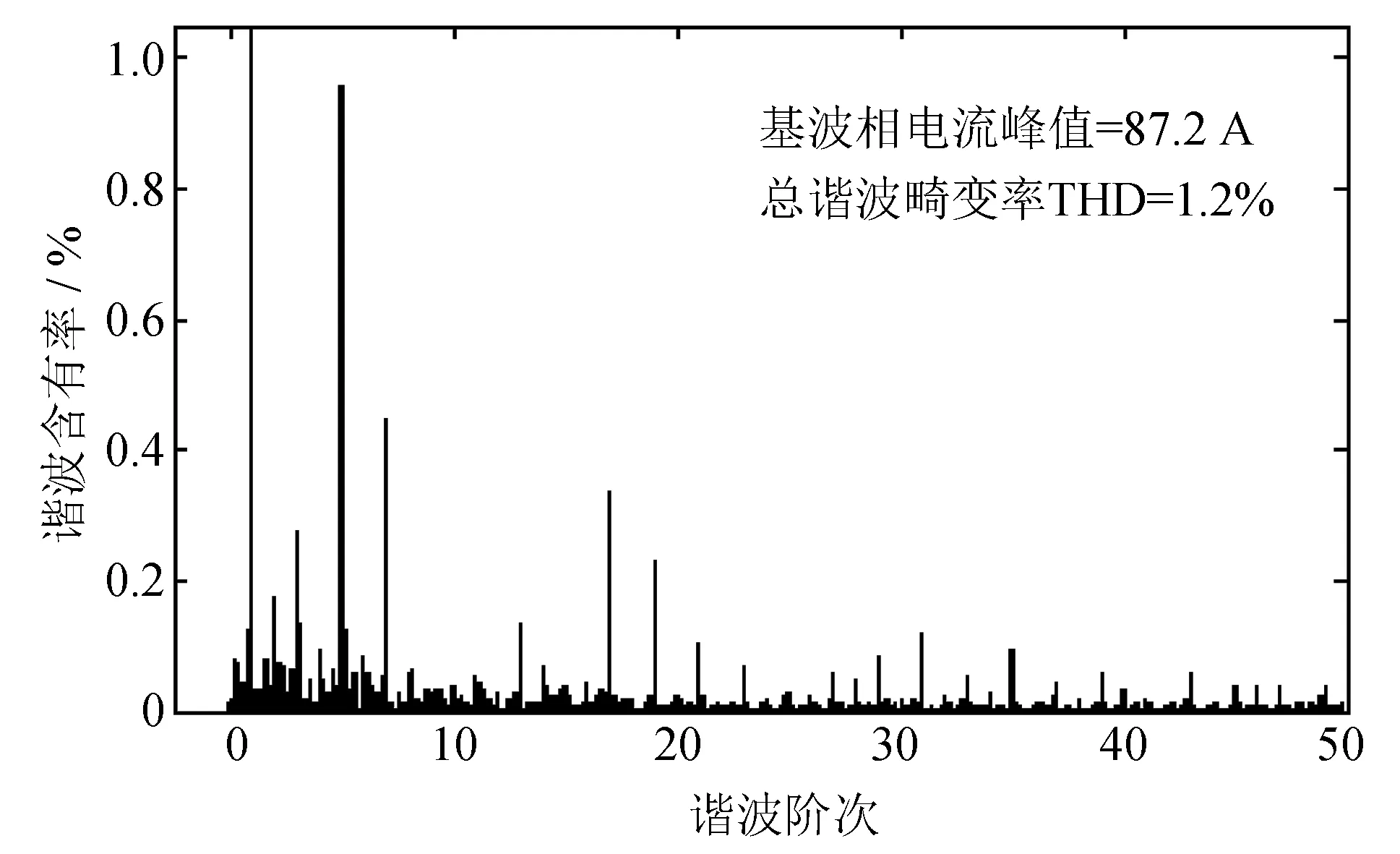
图10 K=1， Rd=1 Ω系统补偿稳定后电网 电流谐波畸变率Fig.10 K=1, Rd=1 Ω, total harmonics distortion (THD) of grid current after current compensation

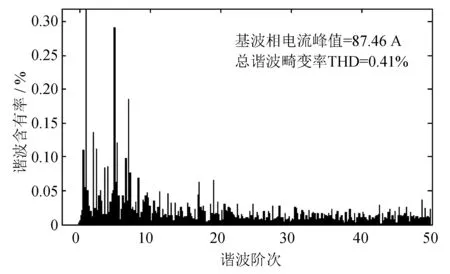
图11 K=3， Rd=1Ω系统补偿稳定后电网 电流谐波畸变率Fig.11 K=3, Rd=1 Ω, total harmonics distortion (THD) of grid current after current compensation

7 结语

1) 当LCL滤波器总电感以及滤波电容设计好时， 从使系统稳定的阻尼电阻、 比例增益可选择范围和滤除开关纹波以及阻尼损耗方面考虑， 逆变器侧电感应该比电网侧电感大.

2) APF双闭环系统的稳态精度， 由外环的重复控制提高， 系统稳定性与单闭环系统相比有所降低， 内环闭环传函作为外环开环传函的一部分， 很大程度上决定着整个双环系统的稳定性. 因此， 在双环系统其它参数已知或设计好的情况下， 可以根据内环闭环传函的波特图， 从抑制LCL谐振入手， 选取比例增益和阻尼电阻， 而后根据外环稳定性的充分条件轨迹图以及仿真效果对所选参数进行修正.

[1] 王兆安, 杨君, 刘进军. 谐波抑制与无功功率补偿[M]. 北京: 机械工业出版社, 2002.

[2] 王盼, 刘飞, 查晓明. 基于有源阻尼的并联有源滤波器设计输出LCL滤波器[J]. 电力自动化设备, 2013, 33(4): 161-166.

[3] 谭理华, 张兴, 杨淑英, 等. 基于陷波算法实现LCL变流器网侧电流直接控制[J]. 电力电子技术, 2010, 44(4): 53-55.

[4] Liserre M, Blaabjerg F, Hansen S. Design and control of an LCL-filter based three-phase active rectifier[J]. IEEE Trans on Industry Applications, 2005, 41(5): 1 281-1 291.

[5] 王要强, 吴凤江, 孙力, 等. 阻尼损耗最小化的LCL滤波器参数优化设计[J]. 中国电机工程学报, 2010, 30(27): 90-95.

[6] 胡金高. 有源滤波器中LCL滤波参数选择和匹配[J]. 福州大学学报: 自然科学版, 2013, 41(6): 1 009-1 015.

[7] 张东江, 仇志凌, 陈天锦, 等. 一种基于相位滞后的并网变流器电流双环控制方法[J]. 电力系统保护与控制, 2011, 39(8): 128-133.

[8] Twining E, Holmes D G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J]. IEEE Transactions on Power Electronics, 2003, 18(3): 888-895.

[9] Abeyasekera T, Johnson C M, Atkinson D J,etal. Suppression of line voltage related distortion in current controlled grid connected inverters[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1 393-1 401.

[10] 王爱华, 张燕燕, 刘晓敏. 永磁直驱风力发电机网侧变换器的研究与仿真[J]. 电源学报, 2012, 40(2): 95-99.

[11] Zhang B, Wang D W, Zhou K,etal. Linear phase lead compensation repetitive control of a CVCF PWM inverter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4): 1 595-1 602.

[12] 仇志凌, 杨恩星, 孔洁, 等. 基于LCL滤波器的并联有源电力滤波器电流闭环控制方法[J]. 中国电机工程学报, 2009, 29(18): 15-20.

[13] 周娟, 秦静, 王子绩, 等. 内置重复控制器无差拍控制在有源滤波器中的应用[J]. 电工技术学报, 2013, 28(2): 233-238.

[14] Tzou Y Y, Ou R S, Jung S L,etal. High-performance programmable AC power source with low harmonic distortion using DSP-based repetitive control technique[J]. IEEE Trans on Power Electronics, 1997, 12(4): 715-725.

[15] Zhou Keliang, Wang Danwei. Unified robust zero-error tracking control of CVCF PWM converters[J]. IEEE Transactions on Circuits System I: Fundamental Theory and Applications, 2002, 49(4): 492-501.

(责任编辑： 沈芸)

Design for LCL-filter-based double-loop control system of shunt APF

SU Zhongyu1， QI Hong1， LI Jinbin1, 2

(1. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China;2. Electronic Information and Electric Engineering Department, Fujian University of Technology， Fuzhou, Fujian 350118, China)

Through theoretical analysis, a design method for LCL-filter-based double-loop control system of shunt active power filter (SAPF) is proposed in this paper. Considering stability of the system, the distribution of inductance between the grid side and inverter side, the selection of damping resistance and proportional gain are put forward combined with a specific example. The simulation with Matlab/Simulink verified the correctness and effectiveness of the proposed design method.

inductance distribution; passive damping; proportional gain; repetitive control

10.7631/issn.1000-2243.2015.04.0488

1000-2243(2015)04-0488-07

2014-06-18

齐虹(1961-)， 教授， 主要从事非线性控制、 电力系统谐波的检测与控制等研究， qihong@fzu.edu.cn

福建省自然科学基金资助项目(2012J01259)

TM762; TP272

A