大规模新能源接入电网连锁故障预防控制策略研究

王维洲，刘茜，但扬清，王耿，刘文颖

(1．国网甘肃省电力公司，甘肃兰州730050;2．国家知识产权局专利局，北京100088; 3．华北电力大学电气与电子工程学院，北京102206)

大规模新能源接入电网连锁故障预防控制策略研究

王维洲1，刘茜2，但扬清3，王耿1，刘文颖3

(1．国网甘肃省电力公司，甘肃兰州730050;2．国家知识产权局专利局，北京100088; 3．华北电力大学电气与电子工程学院，北京102206)

本文着眼于大规模新能源接入的电网连锁故障预防控制策略研究，在深入分析大规模新能源接入对电网连锁故障影响机理的基础上，提出了适应含大规模新能源的电网连锁故障预防控制策略。该控制策略采用直流灵敏度法甄选出高危线路，并计算出发电功率转移分布系数矩阵，继而采用反向等量配对法，根据发电功率转移分布系数调整发电机组的出力，使得高危线路的负载率得到有效下降，同时保证其他线路负载率维持在重载阈值以下，改善潮流分布，起到预防连锁故障发生的作用。最后通过甘肃酒泉地区电网的仿真分析，进一步揭示了大规模新能源接入对电网连锁故障的影响机理;验证了本文提出的连锁故障控制策略的有效性。

电网连锁故障;大规模新能源接入;潮流熵;直流灵敏度;反向等量配对原则

1 引言

随着电网互联程度的加深和大规模新能源的接入，在取得较大经济效益的同时，电网的整体安全性却受到了严重的影响。大规模新能源的随机性和波动性对局部电网的某些故障可能起到推波助澜的作用，从而诱发连锁故障，导致大面积停电事故甚至是电网的崩溃。因此，如何预防连锁故障的发生成为当前国内外学者广泛关注的研究课题。

但是，目前关于连锁故障的预防控制策略的研究，大部分都基于传统电网(不含新能源)进行。然而，近年来随着节能减排和气候变化压力的增大，各国开始着力发展新能源，其中风电尤其受到青睐［1］。由于新能源具有波动性和随机性的特点，其对连锁故障的影响机理尚不明确，对基于大规模新能源接入的复杂电网的连锁故障预防控制方法进行研究具有重要的现实意义。因此，本文从潮流熵的角度考察了大规模风电并网运行对连锁故障的影响;基于风电出力特性提出了适合含大规模风电的电网连锁故障预防控制策略，旨在改善潮流分布，抑制含新能源电网连锁过载效应的出现，并最终降低连锁故障发生的可能性。

2 风电接入对连锁故障的影响机理

2.1 连锁故障发展过程

典型的由连锁故障引发的电力系统崩溃事故，一般分为连续故障阶段、快速连锁故障阶段、停电阶段和恢复阶段四个阶段［2-4］。在整个演变过程中，系统在连续故障阶段时仍处于一种可控状态，而且相继故障之间的时间间隔较长，是连锁故障预警及控制的关键阶段。如果能在该阶段，快速筛选出连锁故障的高危线路并采取行之有效的控制措施，就可以防止连锁故障的发生。

2.2 连锁故障与潮流熵

连锁故障的发展过程中，潮流分布的变化是关键因素。正是某一元件的故障导致潮流大范围转移，致使其他元件的潮流发生改变，潮流分布随之改变，若元件的潮流增加至其动作区域内，则会导致这些元件的相继跳闸。研究表明，潮流分布均匀的电网发生连锁故障的风险远小于潮流分布不均匀的电网［5-7］。潮流分布的均匀与否可由潮流熵［5］来描述。

式中，Nl为线路数。

给定常数序列U=［0，u，2u，…，ku，(k+1)u，…，nu］，nu=100%，对于过载线路负载率不再细分，均置于(nu，(n+1)u］区间。用lk表示负载率处于(ku，(k+1)u］区间内的线路条数，则线路负载率处于(ku，(k+1)u］区间的概率p(k)为:

由熵定义与式(2)得电力网络潮流熵HP为:

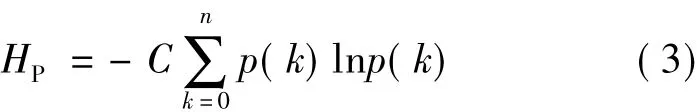
式中，C为熵权值，一般取ln10。

根据潮流熵的定义可知，当电网潮流分布完全均匀(所有线路负载率均相等)时，线路负载率处于某一区间的概率为1，其他则为零，此时潮流熵为零，为最小值;当电网潮流分布完全不均匀(各线路负载率互不相等)时，潮流熵则会偏大。因此连锁故障与潮流熵的关系可以叙述如下:电网潮流熵越小，发生连锁故障的风险也越小。

2.3 风电接入对连锁故障的影响机理

一般来说，系统在稳态运行时，常规电源的出力可基本维持恒定不变，不会引起大范围的功率波动，继而引起潮流熵的大范围波动。而大规模风电出力则可能会处于零出力与最大出力之间的任意值，大范围的出力变化必然带来潮流熵的大幅度变化。

大规模风电集中接入前，线路的负载率集中于某几个负载率区间，处于高负载率区间和低负载率区间的线路都很少。大规模风电集中接入后，由于风电的随机性和波动性，若风电出力瞬时增加，会造成接入点附近潮流较重，周围线路负载率迅速提高，为保持平均负载率不变，则水电和火电等常规电源的出力会相应减小，相邻线路负载率降低;同理，若风电出力瞬时减小，则接入点周围线路负载率会迅速减小，其他常规发电厂的出力则会相应提高，相邻线路负载率升高。也就是说，风电功率波动使处于高负载率区间和低负载率区间的线路条数大大增加，潮流分布变得很不均衡，而且风电规模越大，这种潮流分布不均匀的趋势越明显。即风电大规模集中接入电网，可能会使电网的潮流熵增大，继而发生连锁故障的风险上升。

3 连锁故障预防控制方法

从潮流熵角度出发进行连锁故障的预防控制，关键在于如何调整线路之间的潮流分布，使之趋于均匀化。线路潮流的调整方法一般有交流灵敏度和直流灵敏度两种方法［8-10］。对于含有大规模风电的电网中，电源的出力变化具有较大波动性，若采用交流灵敏度方法，潮流难以收敛，灵敏度矩阵计算难度大。因此，本文采用能够适应大规模风电的直流灵敏度法，首先求取支路相关因子，据此确定连锁故障高危线路，并计算高危线路的有功调整量。在此基础上，利用反向等量配对原则，基于发电功率转移分布系数矩阵调整高危线路的潮流，从而改善电网的潮流分布，降低连锁故障发生的可能性。

3.1 直流灵敏度法

直流灵敏度法［11］以直流潮流方程为基础。直流潮流的矩阵形式如下:

式中，B是以1/xij为支路导纳建立起来的n×n阶节点导纳矩阵;P为节点注入有功列向量;θ为电压相角列向量。

另外，线路l(i，j)有功潮流Pij为:

式中，θi、θj为支路两端节点i、j的电压相角;θij为相角差;xij为支路电抗;Bij为支路导纳。

将式(5)写成矩阵形式:

式中，BL为各支路导纳组成的对角阵;PL为支路有功潮流列向量;Ф为支路两端电压相角差的列向量。

设由网络获得的支路-节点关联矩阵为A。A的每一行对应于电网中的一条支路，有功潮流从i节点流向j节点的支路l(i，j)对应的行中，第i列元素取为1，第j列元素取为－1，其他元素均为0。设网络节点数为n，支路数为L，则A矩阵为L×n阶，即:

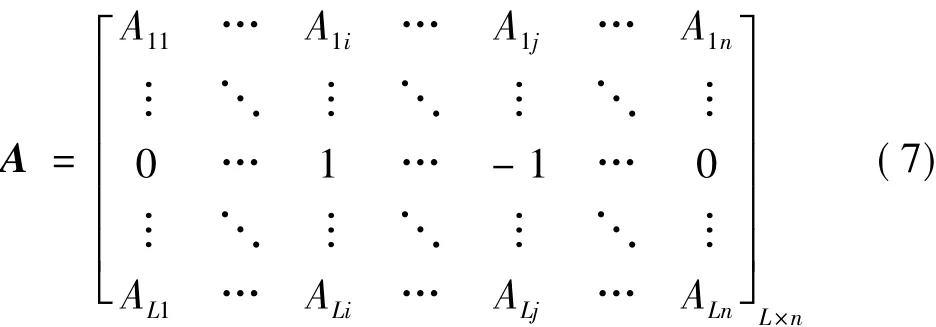
则有Φ=Aθ。又由于θ=B－1P，所以，

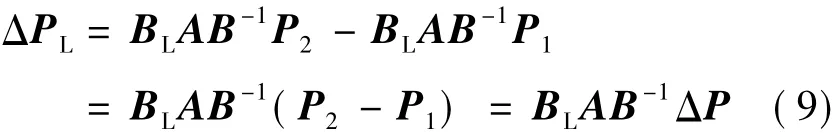
式中，P1及P2是节点注入有功变化前后的向量; ΔP是节点注入功率的调整量;ΔPL是支路有功潮流的改变量。

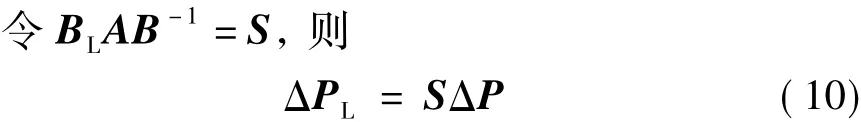
矩阵S就是直流灵敏度法的灵敏度矩阵。

3.2 连锁故障高危线路的甄别

首先计算支路相关因子。设将支路l(i，j)开断，且开断前支路有功潮流为P，如图1所示。

图1 线路l(i，j)的有功潮流Fig．1 Power flow of line

由补偿原理可知，该支路的开断相当于在原网络的i和j节点注入有功功率P和－P。表示节点注入有功变化量ΔP的矩阵形式如下:

由式(11)计算可得任一非开断线路l(k，m)对开断线路l(i，j)的支路相关因子μ为:

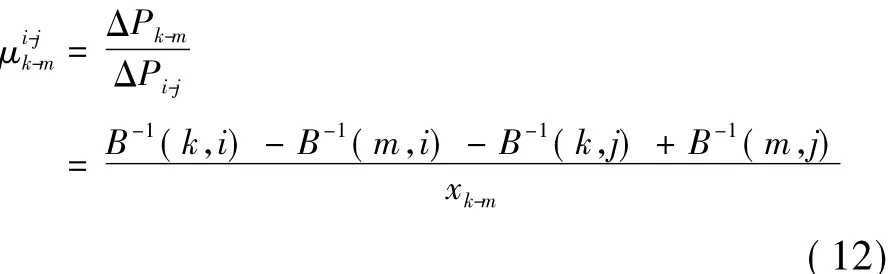
然后，利用支路相关因子求非开断线路(以l(k，m)为例)的有功潮流变化量ΔPk-m，并利用开断线路l(i，j)前的有功潮流，求其开断后其余线路的有功潮流变化量ΔP'k-m和负载率ηk-m为:

设β为线路的重载阈值，当非开断线路的负载率ηk-m＞β时，则开断线路l(i，j)即为连锁故障的高危线路。

基于以上步骤，对全网线路逐一开断和计算，甄别并确定连锁故障的高危线路。

3.3 确定高危线路的有功调整量

为防止高危线路的开断导致其他线路因过载而出现连锁过载跳闸，需要降低高危线路输送的有功功率。

设高危线路为l(i，j)，其开断后重载线路集S为{l1，l2，…，lt}。则对于任一重载线路ls(k，m)，为防止其因l(i，j)的开断而重载，l(i，j)的有功调整量ΔP为:

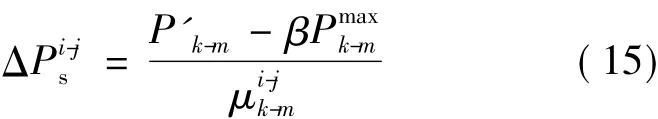
为保证全部重载线路不因线路l(i，j)的开断而重载，则l(i，j)的实际有功调整量ΔPi-j为:

利用上述方法就可以获得全部高危线路对应的有功调整量。

3.4 发电功率转移分布系数矩阵

发电功率转移分布系数(GSDF)［11］表征发电机出现有功功率变化时，导致支路中有功功率变化的灵敏度。发电机h改变有功出力时，对支路l(k，m)的发电功率转移分布系数为:

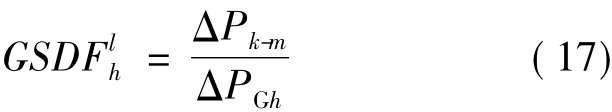
式中，ΔPGh为发电机h有功出力变化量。利用上述的直流灵敏度方法可求得GSDF的矩阵形式:

式中，I为由0和1组成的n×H矩阵，H为发电机总台数。式(18)展开后，得到:

式中，h(h=1，2，…，H)为对应发电机节点号。矩阵GSDF就是线路有功潮流对发电机有功出力的灵敏度矩阵。

3.5 改善潮流分布

(1)控制节点的分类

依据反向等量配对原则［12］可知:若＜0，则发电机Gh增加有功出力时，线路l有功潮流减少，因此对应节点称为加出力节点;若＞0，则发电机Gh减少有功出力时，线路l有功潮流减少，因此对应节点称为减出力节点。

(2)调整原则

根据反向等量配对原则，为了保证系统的总有功出力不变，系统加出力机组G+所增加的有功出力与系统减出力机组G－所减少的有功出力应基本相等。

(3)发电机有功出力的调整量

但是，为防止因改变发电机有功出力而造成其他正常线路过载，则当加减出力机组有功出力对正常线路l(k，m)有功潮流灵敏度S和S满足

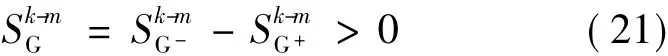
又由于加减处理机组处理调整还会受到发电机本身出力上限ΔP和ΔP的限制，所以控制节点对的实际调整量为:

如此循环，从灵敏度最大的加减出力机组节点对调起，从大到小依序调整，直到满足高危线路的有功调整量或所有可调发电机节点均参与调整时退出。连锁故障预防控制流程如图2所示。

4 实例仿真分析

4.1 甘肃酒泉地区电网简介

截止2012年底，酒泉地区风电装机容量达到586.96万kW，加上火电机组和水电机组等常规能源，酒泉地区的出力已经远远超过当地负荷吸纳能力。而甘肃酒泉千万千瓦级风电基地距离兰州负荷中心的平均距离约为1000 km［13］，如果考虑在西北区域内消纳风电，距离负荷中心的平均距离更远，因此甘肃酒泉地区风电都要通过长线路、远距离送出。其电网接线图如图3所示。

图2 连锁故障预防控制流程图Fig．2 Cascading failure prevention and control flow chart

图3 酒泉地区电网接线示意图Fig．3 Geographic connection diagram of Jiuquan district’s grid

如图3所示，酒泉风电接入和送出通过各风电场以35kV集电线路打捆升压至330kV电压等级变电站，汇集到750kV敦煌和酒泉变，并通过河西走廊的750kV双回交流线输电走廊与甘肃主网联接，为典型的链式长距离供电网络，并且750kV输电通道是新疆外送和风电送出的公共通道。

4.2 仿真计算分析

仿真计算以酒泉地区电网2012年冬季大负荷运行方式为例，首先设风电出力为0，逐步增加风电出力比例，计算酒泉地区电网潮流熵统计结果，如表1所示。

由表1可知:

(1)当风电出力比例为0.3时，潮流熵最小。表明在此时，电网运行状态相对更为安全稳定。

(2)风电出力比例小于0.3时，随着风电出力的增加，潮流熵呈下降趋势，这是由于增加风电出力，可减小远距离送入功率，风电出力就地消纳，此时，电网不容易发生连锁故障;风电出力比例超过0.3以后，风电就地消纳能力饱和，风电需要远距离送出，潮流熵又开始增大，电网发生连锁故障的风险增大。

表1 风电出力比例变化时酒泉地区电网潮流熵统计Tab．1 Statistics on power flow entropy in Jiuquan grid via wind power ratio variations

(3)酒泉风电出力比例达到当前风电机组满出力的0.7倍时，潮流熵急剧增长为1.27，表明随着更大规模风电的集中接入，潮流熵将会迅速增加，电网发生连锁故障的风险骤增，安全运行的压力骤升。

实际上，当风电出力为1200MW，即风电出力比例为1200/4900=24.5%时，酒泉地区出力和负荷大致相等，即风电就地消纳。计算风电出力比例为24.5%时的潮流熵为0.967，小于风电出力比例为30%时的潮流熵0.98。表明风电出力比例为24.5%时，酒泉电网运行状态相对最为安全稳定。

4.3 酒泉地区电网连锁故障预防控制策略

根据本文给出的连锁故障高危线路的甄别方法，以酒泉电网2012年冬大运行方式为基础，调节风电出力进行仿真计算，得到高危线路列表如表2所示。

表2 酒泉电网高危线路列表Tab．2 Lines at high risk in Jiuquan grid

根据本文提出的潮流调整方法，针对瓜嘉330线的开断，进行潮流调整，改善潮流分布，得到控制策略如表3所示。

表3 瓜嘉330线路开断后潮流控制策略Tab．3 Strategy of control of power flow after disconnection of line Guajia 330

经表3中4轮次的调整，再次断开瓜嘉330线，不会引起任何线路过载和电源送出受阻问题，即不会引起连锁故障的发生。

对所有高危线路进行潮流调整前，酒泉电网潮流熵为1.13，调整后，酒泉电网潮流熵变为1.04。可见，调整后潮流熵明显下降，对酒泉电网连锁故障的发生起到了一定的抑制和预防作用。

5 结论

本文着眼于大规模风电接入下的连锁故障预防控制策略研究，得到结论如下:

(1)大规模风电的接入对电网连锁故障的影响与风电接入比例紧密相关，当风电接入比例接近就地消纳阈值时，发生连锁故障的风险最小;接入比例大于或小于该阈值时，都会增加电网发生连锁故障的风险。

(2)采用本文提出的适合含新能源电网的连锁故障预防控制策略，能够有效降低电网的潮流熵值，抑制和预防连锁故障的发生。

［1］中国可再生能源学会风能专业委员会(Wind Committee，China Renewable Energy Society)．2012年中国风电装机容量统计(China’s wind power installed capacity in 2012)［R］．

［2］朱旭凯，刘文颖，杨以涵，等(Zhu Xukai，Liu Wenying，Yang Yihan，et al．)．电网连锁故障演化机理与博弈预防(Evolution mechanism and preventing strategies for cascading failure)［J］．电力系统自动化(Automation of Electric Power System)，2008，32(5):29-33．

［3］王光增(Wang Guangzeng)．基于复杂网络理论的复杂电力网络建模(Research on complex power gridmodeling based on complex network theory)［D］．杭州:浙江大学(Hangzhou:Zhejiang University)，2009.13-50．

［4］梁才，刘文颖，温志伟，等(Liang Cai，Liu Wenying，Wen Zhiwei，etal．)．电网组织结构对其自组织临界性的影响(The influences of power grid structure on selforganized criticality)［J］．电力系统保护与控制(Power System Protection and Control)，2010，38 (20):6-11．

［5］曹一家，王光增，曹丽华，等(Cao Yijia，Wang Guangzeng，Cao Lihua，et al．)．基于潮流熵的复杂电网自组织临界态判断模型(An identification model for self-organized criticality of power grids based power flow entropy)［J］．电力系统自动化(Automation of Electric Power Systems)，2011，35(7):1-6．

［6］于群，曹娜，郭剑波(Yu Qun，Cao Na，Guo Jianbo)．负载率对电力系统自组织临界状态的影响分析(A-nalysis on influence of load rate on power system self-organized criticality)［J］．电力系统自动化(Automation of Electric Power Systems)，2012，36(1):24-27，37．

［7］曹一家，陈彦如，曹丽华，等(Cao Yijia，Chen Yanru，Cao Lihua，et al．)．复杂系统理论在电力系统中的应用研究展望(Prospects of studies on application of complex system theory in power systems)［J］．中国电机工程学报(Proceedings of the CSEE)，2012，32 (19):1-9．

［8］王乐(Wang Le)．脆弱性分析在电力系统安全防御中的应用研究(Application study on vulnerability assessment in power system security defense system)［D］．北京:华北电力大学(Beijing:North China Electric Power University)，2005．

［9］朱旭凯(Zhu Xukai)．电力系统连锁反应故障的预防与控制研究(Research on prevention and control of cascading failure in power system)［D］．北京:华北电力大学(Beijing:North China Electric Power University)，2008．

［10］邓慧琼，艾欣，罗啸(Deng Huiqiong，Ai Xin，Luo Xiao)．电网连锁故障防治策略初探及连锁过载识别方法研究(Discussion on strategy for cascading outages and identifyingmethod of cascading overload)［J］．现代电力(Modern Electric Power)，2007，24(1):5-11．

［11］刘升(Liu Sheng)．电网可用输电能力的研究(Research on the available transfer capability of the power system)［D］．北京:中国电力科学研究院(Beijing: China Electric Power Research Institute)，2008.12-31．

［12］姚峰，张保会，周德才，等(Yao Feng，Zhang Baohui，Zhou Decai，et al．)．输电断面有功安全性保护及其快速算法(Active power security protection of transmission section and its fast algorithm)［J］．中国电机工程学报(Proceedings of the CSEE)，2006，26 (13):31-36．

［13］汪宁渤，马彦宏，夏懿(Wang Ningbo，Ma Yanhong，Xia Yi)．甘肃酒泉10 GW级风电基地面临的巨大挑战(Enormous challenges for Gansu Jiuquan 10 GW wind power base)［J］．电力建设(Electric Power Construction)，2010，31(1):101-104．

Study of strategy to prevent and control power grid cascading failure connecting large-scale new energy

WANGWei-zhou1，LIU Qian2，DAN Yang-qing3，WANG Geng1，LIUWen-ying3
(1．State Grid Gansu Electric Power Company，Lanzhou 730050，China;2．Patent Office State Intellectual Property Office，Beijing 100088，China;3．School of Electrical＆Electronic Engineering，North China Electric Power University，Beijing 102206，China)

This article aims to prevent and control cascading failures of power grid connecting large-scale new energy sources．Based on analysis of the cascading failuresmechanism influenced by large-scale new energy grid-connection，a strategy to preventand control cascading failurewas proposed，which can adapt to themassive new energy grid-connection．It is based on the DC sensitivitymethod to identify the critical lines of cascading failureswhich is also the first failure，and to calculate generation shift distribution factor(GSDF)matrix，then to adjust the power of unit according to GSDFmatrix．This strategy formulates the adjustment of generators’active power according to the sensitivity analysis and to the reverse same-amount pairing principle，in order to improve the power flow distribution of the system and prevent the occurrence of cascading failures．Finally，the cascading failuresmechanism influenced by large-scale new energy grid-connected is further revealed by simulating the Jiuquan grid，and the strategy proposed is validated．

cascading failures;large-scale new energy grid-connection;power flow entropy;DC sensitivity;reverse same-amount pairing principle

TM71

A

1003-3076(2015)03-0012-06

2013-09-23

王维洲(1967-)，男，甘肃籍，正高级工程师，硕士，从事电力系统自动化和继电保护知识产权类科技管理工作;刘茜(1988-)，女，山东籍，工程师，硕士，从事电工领域专利审查工作。