气体绝缘输电线路温升特性有限元分析

靳一林，舒乃秋，邹怡，别芳玫，田双双，邵翠玲，文志强

(武汉大学电气工程学院，湖北武汉430072)

气体绝缘输电线路温升特性有限元分析

靳一林，舒乃秋，邹怡，别芳玫，田双双，邵翠玲，文志强

(武汉大学电气工程学院，湖北武汉430072)

由于气体绝缘输电线路(Gas-Insulated transmission Lines，GIL)的载流能力与温度相关，本文提出了一种基于有限元分析的GIL温升计算方法。为了研究GIL的负荷电流、气体压强、绝缘气体类型以及导体直径四种参数对GIL温升的影响，建立了二维电磁场分析模型，根据流体力学理论，建立了温度场分析数学模型，并给出了模型求解域及边界条件。利用有限元法迭代求解数学模型，获得了在不同参数下的GIL稳态温度场分布，并探讨不同参数对GIL温度变化的成因、变化趋势以及影响，为GIL的参数优化提供了参考。对比实验数据与模型的仿真结果，验证了模型的有效性。

气体绝缘输电线路;温升;电磁场;温度场

1 引言

GIL不仅具有与架空线路相当的传输能力，还具有低电阻损耗、低电容负载、可靠性高、安全环保、使用寿命长等显著优势［1-4］。GIL可以代替架空线路和电缆广泛地应用于电网中。使用GIL时，其导体和外壳上均会产生大量热量，导致温度升高，直接影响GIL的载流能力，需要对GIL温升特性展开更加深入地研究。

国内外学者已经对GIL以及GIS母线、母线槽等的温升问题展开了研究［5-10］。目前，应用于温升问题的求解方法主要分为:实验法、解析法以及有限元分析法。实验法可以准确反映当前实验状况下研究对象的温升，但应用范围受实验条件的限制，不能进行一般性的推广应用［5］。工程上研究温升问题常使用的方法是解析法［6，7］，其计算结果不能较准确地反应GIL内部温度的实际变化，这是因为解析法将对流换热系数设置为常数，不能反映实际环境对温升的影响。有限元分析法被广泛应用于分析、解决电磁场及温度场的问题中［8-10］。通过对有限元中每个单元建立的方程进行联立求解，得出近似的场分布。本文提出一种用于研究GIL的稳态温升的有限元模型。通过对比模型仿真数据与实验数据验证了模型的有效性，并给出了GIL温度近似分布图。利用模型分析了不同负荷电流、气体压强、绝缘气体类型以及导体直径对GIL温升的影响，为GIL的参数设计提供了理论依据。

2 气体绝缘输电线路数学模型

2.1 GIL结构示意图

常见的GIL是由高电导率的铝合金材料的导体，铝合金材料的外壳，支持导体内部绝缘子，分隔相临隔室的绝缘子，绝缘气体以及伸缩节等组成的。图1为GIL的简化横截面示意图，其中标出的测试点1～4为下文仿真中数据点的具体位置，GIL外围为空气。测试点1～4所指位置分别为导体外表面顶端、导体外表面底端、外壳外表面顶端以及外壳外表面底端。

2.2 电磁场数学模型

本文假设导体为标准几何圆形，且外壳与导体同轴。选取GIL横截面以及其外围的空气为求解域。假设空气的外层边界足够远，不受GIL温度变化的影响。忽略端效应及位移电流。

GIL求解区域的电磁场模型可以用麦克斯韦方程组表示。

图1 GIL横截面结构示意图Fig．1 Cross-sectional schematic of GIL

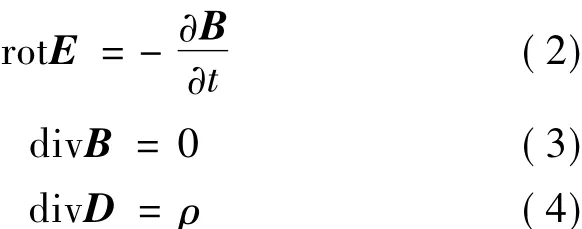
式中，H为磁场强度矢量;B为磁通密度矢量;E为电场强度矢量;D为电位移矢量;δ为电流密度矢量;ρ为电荷体密度。由于GIL模型在工频交流电下运行，场强随时间的变化较慢，位移电流密度与传导电流密度相比可以忽略不计，所以文本GIL模型只考虑磁场变化所产生的电场，不考虑电场变化产生的磁场。

本文研究的是二维GIL模型，求解域中的几何参数、物理参数沿z轴方向均无变化。若将麦克斯韦方程组直接作为电磁场的控制方程，需要联立求解矢量方程，每个矢量方程均包含两个标量方程，并且涉及不同的场矢量，这会导致计算量过于庞大。为了减少控制方程未知数的个数从而减小计算规模，引入矢量磁位A，矢量磁位只有z轴方向分量，即:

将式(5)代入式(1)中，得到:

其中，μ为GIL导体的磁导率。

为了简化计算，可以将电流密度看作源电流和涡电流两部分的组成。源电流区的电流密度大小及分布与GIL负荷电流大小以及导体尺寸有关;涡电流区的电力密度与GIL导体的磁导率相关。

式中，δs和δe分别为源电流和涡电流;σe为GIL导体的电导率。

将式(5)代入式(2)中，由于时间导数与旋度的运算顺序可以交换，得出:

式(9)为一个无旋的矢量场，对于任一标量函数，其梯度的旋度恒为零，因此GIL的电场强度矢量为:

由于电流方向为z轴方向，电场是沿xy平面，沿z轴方向无变化，所以可以忽略标量电位，则式(11)可写为:

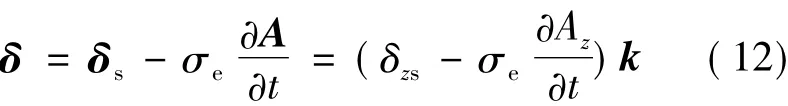
2.3 流体场及温度场数学模型

GIL的热量通过热传导、热对流以及热辐射这三种方式由导体传递给外壳并扩散到空气中。为了减小传统GIL温度分析模型中对流换热系数取为恒定值所带来的误差，本文将求解区域扩展到GIL周围空气进行求解。建立温度场模型时忽略风速以及太阳辐射、绝缘气体的辐射散热。绝缘气体和空气除了比热为常数外，其密度、粘度以及导热系数均与温度有关。

GIL中的绝缘气体或外围空气的密度、粘度和导热系数计算如下:

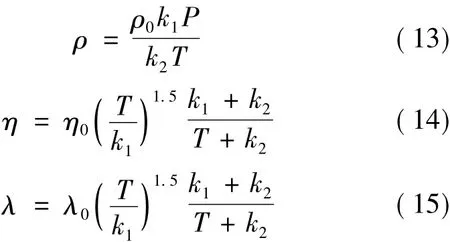
式中，P为压强;ρ、η以及λ分别为气体的密度、粘度和导热系数;ρ0、η0以及λ0分别为SF6气体、N2或者空气在室温下的密度、粘度和导热系数;k1、k2为与室温下气体物性参数相关的定值。

对于均匀不可压缩粘性流体，绝缘气体以及空气都需考虑瞬态流动，GIL对流换热方程可以表述为:

式中，u为气体的速度矢量;u、v为气体在x、y上的速度矢量的分量;fy为作用在y轴上力的大小;Cf为比热容;Q为体积热源。

GIL的导体与外壳及外壳与环境之间不仅存在对流换热的热量交换形式，还存在辐射换热。GIL的不同表面之间的辐射换热的表达式如下:

式中，Ai为单元i的面积;ε为表面发射率(黑度);σ为Stefan-Boltzmann常数;Fij为角系数;Ti为单元i的温度;Tj为单元j的温度。

考虑到GIL外表面的能量平衡，辐射换热的边界条件表达如下:

式中，Tt为外壳温度;Ta为环境温度。

GIL的导体与外壳的辐射换热的边界条件为:

式中，Tc为导体温度;Tf为绝缘气体温度。

在外边界施加恒温值，在固体、流体交界面为无滑移边界即速度矢量均为0。

3 温度场的计算结果及分析

有限元法求解问题的方法是将有限元模型中的求解区域划分成有限个单元，并对每个单元建立电磁场和温度场的控制方程。在考虑到负载和约束情况下对这一系列的方程联立求解，可以求得GIL的电磁场和温度场近似分布图，具体步骤如下所示:

(1)设定环境温度值即初始温度值Ta。

(2)根据式(1)～式(12)建立有限元电磁场模型，将初始温度值代入模型中，进行参数设置，求解导体和外壳的电导率，计算功率损耗结果。

(3)根据式(13)～式(19)将结果作为载荷，代入温度场以及涡流场中，并根据式(20)、式(21)施加边界条件，进行对流换热分析以及辐射换热的分析。

(4)将求解后的温度值与前一次迭代温度值(第一次计算则与初始设定温度值)进行比较，判断温度误差是否小于5%。

(5)若满足误差允许范围，则迭代结束;否则，将温度值作为下一轮迭代初始值，继续进行计算分析。

(6)输出GIL的温度分布图。

文献［7］采用实验法主要从三种运行条件下研究GIL温升特性，分别为在固定环境温度值下的温升特性，在环境温度变化下的温升特性以及在GIL安装角度变化下的温升特性。本文选取与文献中的相同的条件参数以及GIL的尺寸材料，在固定的环境温度值下进行仿真验算。根据式(13)～式(15)，GIL中不同的材料特性列于表1。

表1 GIL的材料特性Tab．1 Material behaviors of GIL

图2为0.35MPa的SF6绝缘气体在8kA的电流下求解区域的温度分布云图。

图2 求解区域的温度分布Fig．2 Temperature distribution of solution region

由图2可以看出，GIL的温度呈对称分布。导体上表面的温度为GIL求解域中温度的最高点，温度为96.1℃，导体的上、下表面温差不大，可以将导体看作等温体。导体和外壳之间的绝缘气体的温度是按梯度分布，温差较为明显，上部分绝缘气体温度高于下部分。这是由于在浮力的作用下，加热的SF6气体上升到GIL的上部分，致使上部分气体流速较高，而下部分的气体几乎处于静止状态。上部分气体通过辐射和对流换热的方式传递热量，即根据式(16)～式(19)求得热量;而下部分气体则通过辐射和热传导的方式进行传递热量，即根据式(13)～式(15)以及式(19)求得热量。由于热传导的效率远低于对流换热，绝缘气体的温度呈阶梯状分布，并使GIL的外壳上、下表面温度为61.4℃以及57.9℃，产生了较大的温差。

表2是将电流强度分别为5kA、7kA以及8kA的仿真值与实验值［5］进行对比，分析得出两者的结果在误差允许的范围内，验证了模型的有效性。

表2 温升实验值与仿真值对比Tab．2 Power losses at different conditions (单位:℃)

4 温升相关的参数分析

本节选取GIL如下标准参数:导体内径、厚度分别为140mm、20mm;外壳内径、厚度分别为470mm、15mm;导体表面的发射率ε为0.9;外壳内、外表面发射率ε分别为0.1和0.9;σ为5.67×10－8W/ (m2·K4);0.35MPa的SF6绝缘气体;电流强度取为8kA;环境温度即初始温度设为29℃并换算为绝对温度值;室温下的导体电导率取为2.78×10－8S/m。改变其中一个参数进行GIL温升特性分析。

4.1 不同负荷电流

改变电流强度值，保持其他参数不变，计算在不同的负荷电流强度下的GIL测试点1～4的温度值。根据仿真值作图3。

图3 不同负荷电流的温度分布Fig．3 Temperature distribution at different load current

从图3可以看出，各测试点温度随着电流强度的增大而升高。由于热传导、自然对流以及辐射的原因，随着电流增强，外壳与导体温差越大并且温升与电流呈非线性关系。这是因为:温度的增加，导致式(14)、式(15)中的气体粘度和导热系数增加，热传导加剧;式(16)～式(18)中的气体速度矢量增大;式(19)表明辐射换热与两个单元温度四次方差有关，不同表面之间的辐射换热量增加。

导体的测试点1、2的温差较小，图3中两条线几乎重合。负荷电流为4kA时，导体最高温度为48.3℃，最低温度为48.2℃;负荷电流为9kA时，外壳最高温度为110.4℃，最低温度110.2℃。外壳的测试点3、4曲线随着负荷电流增长，温差逐渐增大。负荷电流为4kA时，外壳温差为0.9℃;负荷电流为9kA时，外壳温差为4.2℃。

4.2 不同气体压强

改变SF6绝缘气体的压强，保持其他参数不变。测试点1～4的仿真数据如表3所示。

表3 不同气体压强的温度分布Tab．3 Temperature distribution at different pressure conditions (单位:℃)

分析表3的数据可知:导体温度随着压强的增加而减小，导体上表面温差约为13℃和3℃，表明趋势明显减缓;导体的上、下表面的温差也随着压强增大逐渐减小。随着气体压强的增加，外壳的温升变化较小;外壳温度上下浮动不超过1℃;外壳的上、下表面温差略有增大，由3.1℃、3.4℃到3.5℃。

根据式(13)以及式(16)～式(18)，绝缘气体压强的增大，导致气体的密度相同倍数增大，直接影响GIL导体的散热，致使GIL导体温度产生显著变化。但导体温度变化程度对导体电阻率影响较小，导致热流密度变化不大，外壳的温度变化较小。

4.3 不同绝缘气体

保持其他压强不变，设置GIL绝缘气体的种类和比例，进行分析。绝缘气体分别取为SF6、SF6/N2(50/50%)的混合气体、SF6/N2(20/80%)的混合气体以及N2四组，仿真数据见表4。

表4 不同绝缘气体的温升值Tab．4 Temperature distribution at different insulation gases conditions (单位:℃)

在相同的电流强度下，对比GIL四个组别的绝缘气体在测试点1和2的温度，组别二的温度最低，为92.9℃;组别三次之，且与组别二的差别甚微;组别四的温度最高，为100.8℃，且与其他组别的温差较大。

在相同的电流强度下，对比这四个组别的绝缘气体在测试点3和4的温度，GIL外壳表面顶端、底端的温度都没有明显的差异;组别一的外壳温度比其他三组别的略低。

外壳通过对流以及辐射方式进行散热。热平衡取决于外壳的发射率。根据能量守恒定律，在外界环境和发射率均无变化时，总换热量不会因为气体的组成变化而变化，所以四种绝缘气体对应的GIL外壳温度无太大差异。综合分析，SF6和N2混合气体的效果最优。

4.4 不同导体直径

改变GIL导体的厚度值，根据测试点1～4的仿真温度值作图4。

图4 不同导体厚度的温升Fig．4 Temperature distribution at different thicknesses of conductor

保持导体外径不变，改变导体的厚度，从图4可看出，导体及外壳的稳态温度值不是单调变化的;当导体厚度较小时，随着导体厚度的增加，导体的温度减小，测试点1的温度值分别为103.6℃、99.8℃、97.0℃;直至厚度为21～23mm时，温度存在最小值，最低温度所对应的导体测试点1、2的温度约为95.6℃、95.5℃，外壳测试点3、4的温度约为61.1℃、57.7℃;当导体厚度继续增加时，导体温度则缓慢增大，导体测试点1的温度值增长为96.1℃、97.5℃。

这是由于在导体的形状、外形尺寸、材料导电性能以及电流频率等条件确定时，影响温升的主要因素是交流电阻值。在GIL导体厚度较小时，交流电阻随着厚度增加而快速的下降;随着厚度继续增加，交流电阻下降速度逐渐减缓;在壁厚增加到约为20mm时，交流电阻略有上升。

导体的厚度变化除了影响交流电阻外，也会影响GIL的散热以及机械强度等因素。实际应用中的厚度不宜大于临界厚度即不超过最低交流电阻所对应的厚度。导体厚度的选择需综合交流电阻、散热以及机械强度等因素。

5 结论

本文建立了一个求解GIL温升特性的有限元模型，给出了GIL求解域的温度分布图，并将模型的仿真结果与实验结果对比，两者在测试点1～4的误差均在本文的允许范围之内，验证了模型的有效性。本文重点研究了负荷电流、气体压强、绝缘气体类型以及导体厚度四种因素对GIL温升的影响。

改变负荷电流，导体和外壳的温度呈非线性增长，其温度变化趋势为优化在线监控系统提供依据。改变气体压强，对导体温度影响较大，对GIL外壳温度无较大影响。改变绝缘气体类型，得到SF6和N2混合气体散热效果较优。改变导体厚度，由于交流电阻存在最小值，导体、外壳温度存在最低点。用不同的导体厚度、气体压强以及绝缘气体的种类，可以分析出GIL导体和外壳的温度变化趋势，为GIL的参数设计提供参考。

［1］尚涛，李果(Shang Tao，LiGuo)．气体绝缘输电线路的特点及其应用(Discussion on the characteristics of GIL and its application in power systems)［J］．南方电网技术(Southern Power System Technology)，2011，5 (1):81-84．

［2］丁斌，徐耀凉，杨宁，等(Ding Bin，Xu Yaoliang，Yang Ning，et al．)．大电流封闭母线磁-流-热场耦合有限元分析(Finite element analysis of coupled magnetofluid-thermal field for large current enclosed bus bar)［J］．高压电器(High Voltage Apparatus)，2010，46 (8):31-34．

［3］汤浩，吴广宁，范建斌，等(Tang Hao，Wu Guangning，Fan Jianbin，et al．)．直流气体绝缘输电线路的绝缘设计(Insulation design of gas insulated HVDC transmission line)［J］．电网技术(Power System Technology)，2008，32(6):65-70．

［4］Kunze D，Knierim V，王学刚，等(Dirk Kunze，Volker Knierim，Wang Xuegang，et al．)．用于发电中心大规模电力输送的气体绝缘输电线路(Gas insulated transmission lines:bulk power transmission in power generation centers)［J］．中国电力(Electric Power)，2007，40(9):87-90．

［5］Minaguchi D，Ginuo M，Itaka K，et al．Heat transfer characteristics of gas-insulated transmission lines［J］．IEEE Transactions on Power Delivery，1986，1(1): 2-9．

［6］Benato R，Dughiero F．Solution of coupled electromagnetic and thermal problems in gas-insulated transmission lines［J］．IEEE Transactions on Magnetics，2003，39 (3):1741-1744．

［7］Xing Weijun，Li Kang，Zhang Guoqiang．Cooling capability of gasmixtures with fluorocarbon in a gas-insulated transmission linemodel［A］．2010 International Conference on Power System Technology［C］．2010．

［8］Benato R，Dughiero F，Forzan M．Proximity effect and magnetic field calculation in GIL and in isolated phase bus ducts［J］．IEEE Transactions on Magnetics，2002，38 (2):781-784．

［9］Kim JK，Hahn SC，Park K Y．Temperature rise prediction of EHV GISbus bar by coupled magnetothermal finite elementmethod［J］．IEEE Transactions on Magnetics，2005，41(5):1636-1639．

［10］Chakir A，Sofiane Y，AqueletN．Long term testofburied gas insulated transmission lines(GIL)［J］．Applied Thermal Engineering，2003，23(13):1681-1696．

Finite-element-analysis for characteristic of tem perature rise in gas-insulated transm ission lines

JIN Yi-lin，SHU Nai-qiu，ZOU Yi，BIE Fang-mei，TIAN Shuang-shuang，SHAO Cui-ling，WEN Zhi-qiang
(School of Electrical Engineering，Wuhan University，Wuhan 430072，China)

As the current carrying capacity of gas-insulated transmission lines is related with temperature，a calculation method of temperature rise based on finite element analysis is proposed．In order to study the effect on the temperature distribution of GIL by various parameterswhich are load current，gas pressure，gas type and diameter of the conductor，this article establishes a two-dimensional electromagnetic field analysismodel．According to the fluid dynamics theory，mathematicalmodel of temperature field analysis is given，aswell as the solution domain and the boundary conditions of thismodel．Using the finite elementmethod solving the givenmodel，temperature distribution of GIL can be obtained about different parameters．Under the various circumstances of the load current，gas pressure，gas type and diameter of the conductor，this paper also analyzes the causes and the impacts on temperature rise of GIL．The result provides a reference design for parameter optimization．Comparing experimental data and simulation results verifies the validity of themodel．

gas-insulated transmission lines;temperature rise;electromagnetic field;thermal field

TM715

A

1003-3076(2015)03-0029-06

2013-11-13

靳一林(1990-)，女，河北籍，硕士研究生，研究方向为电力设备在线监测及故障诊断;舒乃秋(1954-)，男，湖北籍，教授/博导，博士，研究方向为电力设备在线检测及故障诊断。